ABSTRACT

We consider a General Relativistic generalized RWs metric, and find a field of Universal rotational global centripetal acceleration, numerically coincident with the value of the Pioneers Anomalous one. Related subjects are also treated. The rotation defined here is different from older frameworks, because we propose a Gaussian metric, whose tri-space rotates relative to the time orthogonal axis, globally.

1. Introduction

Detailed description of the subjects treated in this paper may be found in the two books recently published by Berman in 2012 [1,2]). Additional paper references are Berman in 2007 [3]; in 2011 [4] and [5]; in 2012 [6]) and with co-authors Costa, (Berman and Costa in 2012 [7]) and with Gomide (Berman and Gomide in 2012 [8] and in form as a Chapter in an edited book [9], by Berman and Gomide.

The subject treated in three papers by Marcelo Samuel Berman in this issue, two of them co-authored by Fernando de Mello Gomide (in 2012 [1]; and the present paper) and one co-authored by Newton C. A. da Costa (in 2012 [7]) are fully covered, along with all introductory material, in the books by Berman recently published (in 2012 [1,2]). Readers which are not familiar with the contents of the three papers in this issue of this Journal, may find relief by consulting those books.

Attempts to ascribe a rotational state to the Universe, were carefully described by Godlowski (in 2011 [10]). However, he confessed that there was no theoretical framework, within General Relativity, to guide the observations. In the present paper,such a mechanism is provided. The metric to be presented, makes the tri-dimensional space, globally rotate relative to the orthogonal time axis. We are now proposing a novel idea, a generalized Gaussian metric, which is minimally different from the Robertson-Walkers one. In Berman [11], a semi-relativistic treatment, based on the zero-total energy of the (rotating) Universe, made us conclude that the Pioneers anomalous deceleration, was a kind of peculiar centripetal effect of the rotation of the Universe, that could be observed by any cosmological observer. In the present paper, we prove the alleged zero-total energy of the rotating Universe, and supply the metric for such rotation with expansion. We keep a perfect fluid model, unlike Raychaudhuri’s vorticities, and we also differ from the metrical rotational states, derived from non-diagonalized metrics. We shall find an energy-density solution, very similar to the Berman [11] solution. As Berman and Gomide (in 2012 [9]) have shown, by our framework, of a rotating Universe, we explain the three NASA anomalies, namely, the Pioneers linear deceleration, the spin-down of the spacecraft when they were undisturbed, and the fly-by. The present paper, yields a Machian solution, while the other one supplies a large class of general relativistic cosmological solutions with Universal rotation [8].

Ni [12,13], has reported observations on a possible rotation of the polarization of the cosmic background radiation, around 0.1 radians. As such radiation was originated at the inception of the Universe, we tried to estimate a possible angular speed or vorticity, by dividing 0.1 radians by the age of the Universe, obtaining about 10^–19 rad·s^–1.

The numerical result is very close to the theoretical estimate, by Berman (in 2007 [11]),

where c, R represent the speed of light in vacuum, and the radius of the causally related Universe.

We must remember, as Berman and Gomide [9] have pointed, that their calculation deals with material particles, or, in the language of General Relativity, non-null geodesics. The fact that the Universe may exhibit a rotating state, can be understood by a simple fine-tuning argument—it would be highly improbable that the Universe could keep since birth a state of no angular momentum at all.

The value of Bermans rotation, fits with the Pioneers anomaly, which consists on decelerations sufferred by Nasa space probes in non-closed curves, extending to outer space. Thermal emission was cited as resolving the Pioneers anomaly, but it does not explain the fly-bys, like Berman and Gomide [9] did through the present rotational theory. Worse, thermal emission is unable to explain why elliptical orbiters do not decelerate accordingly.

About this same numerical value of the angular speed is predicted also in Godel’s rotational model, but it is not an expanding one (see Adler, Bazin and Schiffer [14]). In the next few years, the observational evidence may confirm or not such rotation .

Rotating metrics in General Relativity were first studied by Islam (in 1985 [15]), but Cosmology was not touched upon. However, it would be necessary an extreme perfect fine-tuning, in order to create the Universe without any angular-momentum. The primordial Quantum Universe, is characterized by dimensional combinations of the fundamental constants “c”, “h” and “G” respectively the speed of light in vacuo, Planck’s and Newton’s gravitational constants. The natural angular momentum of Planck’s Universe, as it is called, is, then, “h”. It will be shown that the angular momentum grows with the expanding Universe, but the corresponding angular speed decreases with the scale-factor (or radius) of the Universe, such being the reason for the difficulty in detection of this speed with present technology. Notwithstanding, the so-called Pioneers’ anomaly (Anderson et al., in 2002 [16]), which is a deceleration verified in the Pioneers space-probes launched by NASA more than thirty years ago, was attributed by Berman, to a “Machian” ubiquitous field of centripetal accelerations, due to the rotation of the Universe. Berman’s calculation rested on the assumption that the zero-total energy of the Universe was a valid result for the rotating case, but the proof was not supplied in that paper (Berman, in 2007 [3]). By “proof”, one thinks on the pseudotensor energy calculations of General Relativity—the best gravitational theory ever published.

In his three best-sellers Hawking (in 1996 [17]; 2001 [18]; 2003 [19]) describes inflation (Guth in 1981 [20] and in 1998 [21]), as an accelerated expansion of the Universe, immediately after the creation instant,while the Universe, as it expands,borrows energy from the gravitational field to create more matter. According to his description, the positive matter energy is exactly balanced by the negative gravitational energy, so that the total energy is zero, and that when the size of the Universe doubles, both the matter and gravitational energies also double, keeping the total energy zero (twice zero). Moreover, in the recent, next best-seller, Hawking and Mlodinow (in 2010) comment that if it were not for the gravity interaction, one could not validate a zero-energy Universe, and then, creation out of nothing would not have happened.

There are four methods, in GRT, to create rotations. Non-diagonal metrics, like Kerrs, is one. The adoption of an imperfect fluid model, with vorticities, as in Raychaudhuris equation, is second. Third, you may follow the Godlowski et al. (in 2004 [22]) idea, and add to the scalefactor s squared time derivative, a rotational term 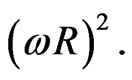On the other hand, Berman (in 2008 [23,24]) has shown that Robertson-Walker’s metric, is a particular, non-rotating case, of a general relativistic expanding and rotating metric first developed by Gomide and Uehara (in 1981 [25]). The peculiarity of the general metric is that instead of working with proper-time, one writes the field equations of General Relativity with a cosmic time t related by:

(1)

where,

(2)

It was seen that when one introduces a metric temporal coefficient 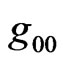which is not constant, the new metric includes rotational effects. In fact, we have a generalized Gaussian metric, because besides the fact that the trispace is orthogonal to the time-axis, the spatial part of the metric, rotates as a whole, relative to this time axis. This is a new concept being introduced in the theory.

The present paper follows the steps of the semi-relativistic treatment by Berman (in 2007 [3]), but this time, it is General relativistic, and we shall find a Machian kind of solution. The general solution is to be found in Berman and Gomide (in 2012 [8]).

In a previous paper Berman (in 2009 [26]) has calculated the energy of the Friedman-Robertson-Walker’s Universe, by means of pseudo-tensors, and found a zerototal energy. Our main task will be to show why the Universe is a zero-total-energy entity, by means of pseudotensors, even when one chooses a variable 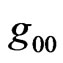such that the Universe also rotates, and then, to show how General Relativity predicts a universal angular speed, and a universal centripetal deceleration, numerically coincident with the observed deceleration of the Pioneers spaceprobes. The first calculation of this kind, with the Gomide-Uehara generalization of RWs metric, was undertaken by Berman (in 1981 [27]), in his M.Sc. thesis, advised by the present second author, but where the rotation of the Universe was not the scope of the thesis.

The pioneer works of Berman (in 1981 [27]), Nathan Rosen (in 1994 [28]), Cooperstock and Israelit, (in 1995 [29]), showing that the energy of the Universe is zero, by means of calculations involving pseudotensors, and Killing vectors, respectively, are here given a more simple approach. The energy of the (non-rotating) RobertsonWalker’s Universe is zero, (Berman, in 2007 [11]; and in 2009 [26]). Berman (in 1981 [27]) was the first author to work, in pseudotensor calculations for the energy of Robertson-Walker’s Universe. He made the calculations on which the present paper rest, and, explicitly obtained the zero-total energy for a closed Universe, by means of LLpseudotensor, when Robertson-Walker’s metric was generalised by the introduction of a temporal-time-varying metric coefficient. However, the present authors, were unaware, in the year 1981, of the exact significance of their findings.

The zero-total-energy of the Roberston-Walker’s Universe, and of any Machian ones, have been shown by many authors (Berman in 2006 [30,31]; in 2007 [11]; 2007 [32]; 2007 [3]). It may be that the Universe might have originated from a vacuum quantum fluctuation. In support of this view, we shall show that the pseudotensor theory (Adler et al. in 1975 [14]) points out to a nullenergy for a rotating Robertson-Walker’s Universe. Some prior work is mentioned, (in 2006 [30]; 2006 [31]; in 2007 [11]; 2007 [32]; 2007 [3]; Rosen in 1995 [33]; York Jr in 1980 [34]; Cooperstock in 1994 [35]; Cooperstock and Israelit in 1995 [29]; Garecki in 1995 [36]; Johri et al. in 1995 [37]; Feng and Duan in 1996 [38]; Banerjee and Sen in 1997 [39]; Radinschi in 1999 [40]; Cooperstock and Faraoni in 2003 [41]). See also Katz (in 2006 [42], in 1985 [43]; Katz and Ori in 1990 [44]; Katz et al. in 1997 [45]). Recent developments include torsion models (So and Vargas in 2006 [46]), and, a paper by Xulu in 2000 [47].

The reason for the failure of non-Cartesian curvilinear coordinate energy calculations through pseudotensors, resides in that curvilinear coordinates carry non-null Christoffel symbols, even in Minkowski spacetime, thus introducing inertial or fictitious fields that are interpreted falsely as gravitational energy-carrying (false) fields.

Carmeli et al. in 1990 [48] listed four arguments against the use of Einstein’s pseudotensor: 1) the energy integral defines only an affine vector; 2) no angular-momentum is available; 3) as it depends only on the metric tensor and its first derivatives, it vanishes locally in a geodesic system; 4) due to the existence of a super-potential, which is related to the total conserved pseudoquadrimomentum, by means of a divergence, then the values of the metric tensor, and its first derivatives, only matter, on a surface around the volume of the mass-system.

We shall argue below that, for the Universe, local and global Physics blend together. The pseudo-momentum, is to be taken like the linear momentum vector of Special Relativity, i.e., as an affine vector. In a previous paper (Berman in 2009 [26]), we stated that “if the Universe has some kind of rotation, the energy-momentum calculation refers to a co-rotating observer”. Such being the case, we now go ahead for the actual calculations, involving rotation. Birch (in 1982 [49] and in 1983 [50]) cited inconclusive experimental data on a possible rotation of the Universe, which was followed by a paper written by Gomide, Berman and Garcia in 1986 [51].

2. Field Equations for the Rotating and Expanding Metric

Consider first a temporal metric coefficient which depends only on t. The line element becomes:

(3)

The field equations, in General Relativity Theory (GRT) become:

(4)

and,

(5)

Local inertial processes are observed through proper time, so that the four-force is given by:

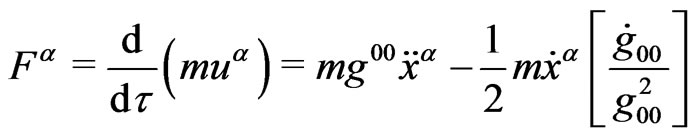(6)

Of course, when, the above equations reproduce conventional Robertson-Walker’s field equations.

We must mention that the idea behind RobertsonWalker’s metric is the Gaussian coordinate system. Though the condition 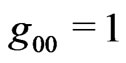is usually adopted, we must remember that, the resulting time-coordinate is meant as representing proper time. If we want to use another coordinate time, we still keep the Gaussian coordinate properties.

From the energy-momentum conservation equation, in the case of a uniform Universe, we must have,

(7)

The above is necessary in the determination of cosmic time, for a commoving observer. We can see that the hypothesis (2)—that is only time-varying—is now validated.

In order to understand Equation (6), it is convenient to relate the rest-mass m, to an inertial mass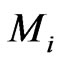, with:

(8)

It can be seen that 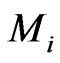represents the inertia of a particle, when observed along cosmic time, i.e., coordinate time. In this case, we observe that we have two acceleration terms, which we call,

(9)

and,

(10)

The first acceleration is linear; the second, resembles rotational motion, and depends on and its timederivative.

If we consider 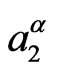a centripetal acceleration, we conclude that the angular speed is given by,

(11)

By comparison between the usual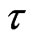—metric, and the field equations in the t—metric, we are led to conclude that the conventional energy density 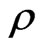and cosmic pressure p are transformed into 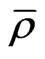and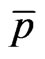, where:

(12)

and,

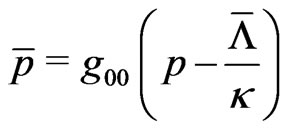(13)

We plug back into the field equations, and find,

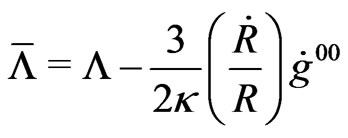(14)

For a time-varying angular speed, considering an arc, so that,

(15)

we find, from (11),

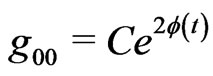(C = constant)   (16)

Returning to (14), we find,

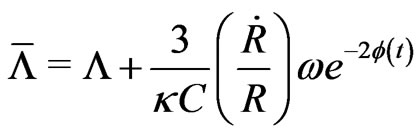(17)

This completes our solution.

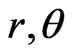The case where depends also on and 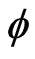was considered also by Berman (in 2008 [24]) and does not differ qualitatively from the present analysis, so that, we refer the reader to that paper.

3. Energy of the Rotating Evolutionary Universe

Even in popular Science accounts (Hawking in 1996 [17]; in 2001 [18] and in 2003 [19]; Hawking and Moldinow in 2010; and Guth in 1998 [21]), it has been generally accepted that the Universe has zero-total energy. The first such claim, seems to be due to Feynman in 1962-3 [52]. Lately, Berman (in 2006 [30,31]) has proved this result by means of simple arguments involving Robertson-Walker’s metric for any value of the tri-curvature ().

The pseudotensor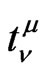, also called Einstein’s pseudotensor, is such that, when summed with the energy-tensor of matter, gives the following conservation law:

(18)

In such case, the quantity

(19)

is called the general-relativistic generalization of the energy-momentum four-vector of special relativity (Adler et al. in 1975 [14]).

It can be proved that is conserved when:

a) only in a finite part of space; andb) when we approach infinity, where is the Minkowski metric tensor.

However, there is no reason to doubt that, even if the above conditions were not fulfilled, we might eventually get a constant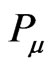, because the above conditions are sufficient, but not strictly necessary. We hint on the plausibility of other conditions, instead of a) and b) above.

Such a case will occur, for instance, when we have the integral in (19) is equal to zero.

For our generalised metric, we get exactly this result, because, from Freud’s (1939) formulae, there exists a super-potential, (Papapetrou in 1974 [54]):

where the bars over the metric coefficients imply that they are multiplied by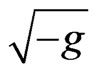, and such that,

thus finding, after a brief calculation, for the rotating Robertson-Walker’s metric,

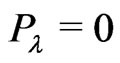
The above result, with von Freud’s superpotential, which yields Einstein’s pseudotensorial results, points to a zero-total energy Universe, even when the metric is endowed with a varying metric temporal coefficient .

A similar result would be obtained from LandauLifshitz pseudotensor (Papapetrou in 1974 [54]), where we have:

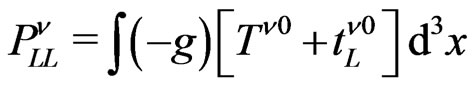(20)

where,

and,

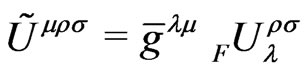
A short calculation shows that, for the rotating metric, too, we keep valid the result,

(21)

Other superpotentials would also yield the same zero results. A useful source for the main superpotentials in the market, is the paper by Aguirregabiria et al. in 1996 [55].

The equivalence principle, says that at any location, spacetime is (locally) flat, and a geodesic coordinate system may be constructed, where the Christoffel symbols are null. The pseudotensors are, then, at each point, null. But now remember that our old Cosmology requires a co-moving observer at each point. It is this co-motion that is associated with the geodesic system, and, as RWs metric is homogeneous and isotropic, for the co-moving observer, the zero-total energy density result, is repeated from point to point, all over spacetime. Cartesian coordinates are needed, too, because curvilinear coordinates are associated with fictitious or inertial forces, which would introduce inexistent accelerations that can be mistaken additional gravitational fields (i.e., that add to the real energy). Choosing Cartesian coordinates is not analogous to the use of center of mass frame in New-tonian theory, but the null results for the spatial components of the pseudo-quadrimomentum show compatibility.

4. An Alternative Derivation

Though so many researchers have dealt with the energy of the Universe, our present original solution involves rotation. We may paraphrase a previous calculation, provided that we work with proper time 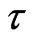instead of coordinate time t (Berman in 2009 [26]). Then, the rotation of the Universe will be automatically included. We shall now consider, first, why the Minkowski metric represents a null energy Universe. Of course, it is empty. But, why it has zero-valued energy? We resort to the result of Schwarzschilds metric, (Adler et al. in 1975 [14]), whose total energy is,

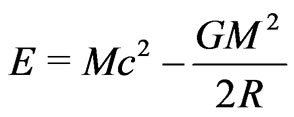
If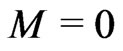, the energy is zero, too. But when we write Schwarzschilds metric, and make the mass become zero, we obtain Minkowski metric, so that we got the zeroenergy result. Any flat RWs metric, can be reparametrized as Minkowskis; or, for closed and open Universes, a superposition of such cases (Cooperstock and Faraoni in 2003 [41]; Berman in 2006 [30,31]).

Now, the energy of the Universe, can be calculated at constant time coordinate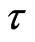. In particular, the result would be the same as when, or, even when. Arguments for initial null energy come from Tryon (in 1973 [58]), and Albrow (in 1973 [59]). More recently, we recall the quantum fluctuations of Alan Guths inflationary scenario (Guth in 1981 [20] and 1998 [21]). Berman (see for instance [57] ), gave the Machian picture of the Universe, as being that of a zero energy. Sciamas inertia theory results also in a zero-total energy Universe (Sciama in 1953 [58]; Berman in 2008 [59] and in 2009 [61]).

Consider the possible solution for the rotating case. We work with the 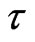-metric, so that we keep formally the RWs metric in an accelerating Universe. The scalefactor assumes a power-law, as in constant deceleration parameter models (Berman in 1983 [64]; and Berman and Gomide in 1988 [65]),

(22)

where, m, D = constants, and,

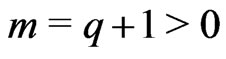(23)

where q is the deceleration parameter.

For a perfect fluid energy tensor, and a perfect gas equation of state, cosmic pressure and energy density obey the following energy-momentum conservation law, (Berman in 2007 [10,32]),

(24)

where, only in this Section, overdots stand for 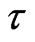-derivatives. Let us have,

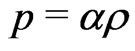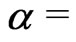(constant larger than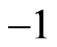)(25)

On solving the differential equation, we find, for any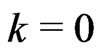, 1, , that,

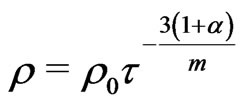(constant)(26)

When, from (26) we see that the energy density becomes zero, and we retrieve an “empty” Universe, or, say, again, the energy is zero. However, this energy density is for the matter portion, but nevertheless, as in this case, 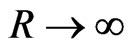, all masses are infinitely far from each others, so that the gravitational inverse-square interaction is also null. The total energy density is null, and, so, the total energy. Notice that the energy-momentum conservation equation does not change even if we add a cosmological constant density, because we may subtract an equivalent amount in pressure, and Equation (24) remains the same. The constancy of the energy, leads us to consider the zero result at infinite time, also valid at any other instant.

We refer to Berman (in 2006 [30,31]) for another alternative proof of the zero-energy Universe. If we took 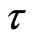instead of t, these references would provide the zero result also for the rotational case.

5. Pioneers Anomaly Revisited

Einstein’s field Equations (4) and (5) above, can be obtained, when 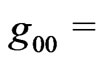constant, through the mere assumptions of conservation of energy (Equation (4)) and thermodynamical balance of energy (Equation (5)), as was pointed out by Barrow in 1988 [66]. The latter is also to be regarded as a definition of cosmic pressure, as the volume derivative of energy with negative sign

.

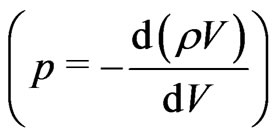Now, let us consider a time-varying. We may write the energy (in fact, the “energy-density”)—equation, as follows:

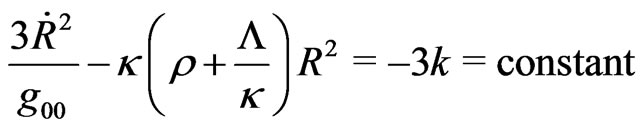(27)

The r.h.s. stands for a constant. We can regard the l.h.s. as the a sum of constant terms, thus finding a possible solution of the field equations, such that each term in the l.h.s. of (27) remains constant. For example, let us consider,

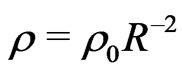(28)

(29)

(30)

where, , and 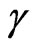are non-zero constants. Relation (28) makes this solution practically of the Machiantype, similar to the semi-relativistic treatment by Berman (in 2007 [3]). More general solutions may be found also in the companion paper by Berman and Gomide (2012) [8] published in this issue of this Journal. See also Berman (in 2011 [4,5]; in 2012 [1,2,6]; Berman and Gomide in 2012 [9]).

When we plug the above solution to the cosmic pressure Equation (5), we find that it is automatically satisfied provided that the following conditions hold,

(31)

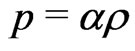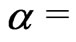(constant(32)

and,

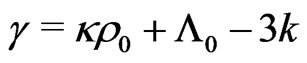(32a)

As we found a general-relativistic solution, so far, we are entitled to the our previous general relativistic angular speed Formula (11), to which we plug our solution (30), to wit,

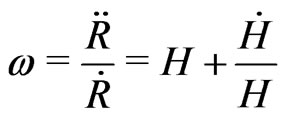
For the power-law solution of the last Section,

so that,

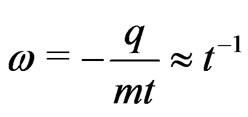
where we roughly estimated the present deceleration paramenter as, while, the centripetal acceleration,

Notice that the same result would follow from a scalefactor varying linearly with time. This is the sort of scalefactor associated with the Machian Universe. In fact,the field equations that we had (Equations (4) and (5)), were not enough in order to determine the exact form of the scale-factor, because we had an extra-unknown term, the temporal metric coefficient. When we advance a given equation of state, the original RWs field equations, with constant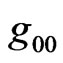, may determine the scale-factors formula. Just to remember, our solution is a particular one.

This is a general relativistic result. It matches Pioneers anomalous deceleration.

In an Appendix to this Section, we go ahead with the alternative calculation with a simple naive Special Relativistic-Machian analysis, as had been made in Berman (in 2007 [3]).

6. Final Comments and Discussion

Someone has made very important criticisms on our work. First, he says why do not the planets in the solar system show the calculated deceleration on the Pioneers? The reason is that elliptical orbits are closed, and localized. You do not feel the expansion of the universe in the sizes of the orbits either. In General Relativity books, authors make this explicit. You do not include Hubbles expansion in Schwarzschilds metric. But, those space probes that undergo hyperbolic motion, which orbits extend towards infinity, they acquire cosmological characteristics, like, the given P.A. deceleration. Second objection, there are important papers which resolve the P.A. with non-gravitational Physics. The answer—that is OK, we have now alternative explanations. This does not preclude ours. Third, cosmological reasons were discarded, including rotation of the Universe. The problem is that those discarded cosmologies, did not employ the correct metric. For instance, they discarded rotation by examining Godel model, which is non expanding, and with a strange metric. The kind of metric we employ now, or the one that we employed in the rotational case, were not discarded or discussed by the authors cited by this objecter. Then, the final question, is how come that a well respected author dismissed planetary Coriolis forces induced by rotation of distant masses, by means of the constraints in the solar system. Our answer is that, beside what we answered above, he needs to consider Machs Principle on one side, and the theoretical meaning of vorticities, because one is not speaking in a center or an axis of rotation or so. When we say, in Cosmology, that the Universe rotates, we mean that there is a field of vorticities,just that. The whole idea is that Cosmology does not enter the Solar System except for non-closed orbits that extend to outer space. We ask the reader to check Machs Principle, because in some formulations of this principle, rotation is in fact a forbidden affaire.

Another one pointed out a different “problem”. He objects, that the angular speed formula of ours, is coordinate dependent. Now, when you choose a specific metric, you do it thinking about the kind of problem you have to tackle. After you choose the convenient metric, you forget tensor calculus, and you work with coordinate-dependent relations. They work only for the given metric, of course.

We have obtained a zero-total energy proof for a rotating expanding Universe. The zero result for the spatial components of the energy-momentum-pseudotensor calculation, are equivalent to the choice of a center of Mass reference system in Newtonian theory, likewise the use of comoving observers in Cosmology. It is with this idea in mind, that we are led to the energy calculation, yielding zero total energy, for the Universe, as an acceptable result: we are assured that we chose the correct reference system; this is a response to the criticism made by some scientists which argue that pseudotensor calculations depend on the reference system, and thus, those calculations are devoid of physical meaning.

Related conclusions by Berman should be consulted (see all Berman’s references at the end of this article). As a bonus, we can assure that there was not an initial infinite energy density singularity, because attached to the zero-total energy conjecture, there is a zero-total energydensity result, as was pointed first by Berman elsewhere (Berman, for instance, see in 2012 [1,2]). The so-called total energy density of the Universe, which appears in some textbooks, corresponds only to the non-gravitational portion, and the zero-total energy density results when we subtract from the former, the opposite potential energy density.

As Berman( in 2009 [67,68]) shows, we may say that the Universe is singularity-free, and was created abnihilo, nor there is zero-time infinite energy-density singularity.

Paraphrasing Dicke (in 1964 [69,70]), it has been shown the many faces of Dirac’s LNH, as many as there are about Mach’s Principle. In face of modern Cosmology, the naif theory of Dirac is a foil for theoretical discussion on the foundations of this branch of Physical theory. The angular speed found by us, (Berman, in 2010 [68]; in 2009 [72]), matches results by Gödel (see Adler et al. in 1975 [14]), Sabbata and Gasperini (in 1979 [70]), and Berman (in 2007 [3], and in 2008 [24,74]).

Rotation of the Universe and zero-total energy were verified for Sciama’s linear theory, which has been expanded, through the analysis of radiating processes, by one of the present authors (Berman in 2008 [59]; and in 2009 [60]).There,we found Larmor’s power formula, in the gravitational version, leads to the correct constant power relation for the Machian Universe. However, we must remember that in local Physics, General Relativity deals with quadrupole radiation, while Larmor is a dipole formula; for the Machian Universe the resultant constant power is basically the same, either for our Machian analysis or for the Larmor and general relativistic formulae.

Referring to rotation, it could be argued that cosmic microwave background radiation deals with null geodesics, while Pioneers’ anomaly, for instance, deals with time-like geodesics. In favor of evidence on rotation, we remark neutrinos’ spin, parity violations, the asymmetry between matter and anti-matter, left-handed DNA-helices, the fact that humans and animals alike have not symmetric bodies, the same happening to molluscs. And, of course, the results of the rotation of the polarization of CMBR.

We predict that chaotic phenomena and fractals, rotations in galaxies and clusters, may provide clues on possible left handed preference through the Universe.

Berman and Trevisan (in 2010 [74]) have remarked that creation out-of-nothing seems to be supported by the zero-total energy calculations. Rotation was now included in the derivation of the zero result. We could think that the Universes are created in pairs, the first one (ours), has negative spin and positive matter; the second member of the pair, would have negative matter and positive spin: for the ensemble of the two Universes, the total mass would always be zero; the total spin, too. The total energy (twice zeros) is also zero. Our framework, is the only one to solve the fly-by anomaly altogether, and explains why elliptical orbiters do not decelerate.

For more details on the subjects treated here, the general recomendation is to refer the reader to both books published recently by Berman (in 2012 [72]).

7. Acknowledgements

One of the authors (MSB) thanks Marcelo Fermann Guimarães, Nelson Suga, Mauro Tonasse, Antonio F. da F. Teixeira, and for the important incentive offered by Miss Solange Lima Kaczyk, now, a brand new advocate, continued during the last five years of his research in Cosmology.

REFERENCES

Appendix to the Fifth Section

As we now have the pseudo-tensorial zero-total energy result, for rotation plus expansion, we might write in terms of elementary Physics, a possible energy of the Universe equation, composed of the inertial term of Special Relativity, , the potential self-energy

, and the cosmological “constant” energy,

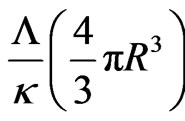, and not forgetting rotational energy, 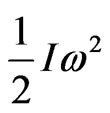where I stands for the moment of inertia of a “sphere” of radius R and mass M. The energy equation is equated to zero, i.e.,

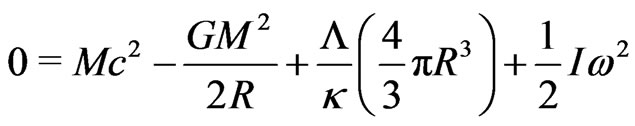(33)

It must be remembered that R is a time-increasing function, while the total-zero energy result must be timeinvariant, so that the principle of energy conservation be valid. A close analysis shows that the above conditions can be met by solutions (28) and (29), which were derived or induced from the general relativistic equations. When we plug the inertia moment,

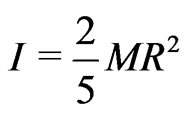(34)

we need also to consider the following Brans-Dicke generalised relations,

(35)

and,

(36)

If we calculate the centripetal acceleration corresponding to the above angular speed, we find, for the present Universe, with 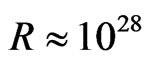cm and 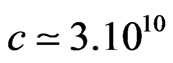cm·s^–2

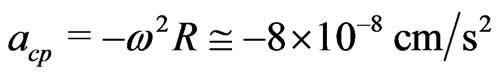(37)

This value matches the observed experimentally deceleration of the NASA Pioneers’ space-probes.

We observe that the Machian picture above is understood to be valid for any observer in the Universe, i.e., the center of the “ball” coincides with any observer; the “Machian” centripetal acceleration should be felt by any observed point in the Universe subject to observation from any other location.

We solve also other mystery concerning Pioneers anomaly. It has been verified experimentally, that those space-probes in closed (elliptical) orbits do not decelerate anomalously, but only those in hyperbolic flight. The solution of this other enigma is easy, according to our view. The elliptical orbiting trajectories are restricted to our local neighborhood, and do not acquire cosmological features, which are necessary to qualify for our Machian analysis, which centers on cosmological ground. But hyperbolic motion is not bound by the Solar system, and in fact those orbits extend to infinity, thus qualifying themselves to suffer the cosmological Machian deceleration. Thermal emission may solve the first Pioneer anomaly, but it does not solve the spin-down, nor the fly-bys in gravity assists. It is not clear why, thermal emission did not cause decelerations in elliptical orbiters. Rotation of the Universe solves all the three (Berman and Gomide in 2012 [8]).