Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21682,5 pages DOI:10.4236/jmp.2012.38098
Matter Waves in a Static Gravitational Field
ACK srl, Pascani, Romania
Email: naga@ack.ro
Received May 16, 2012; revised June 9, 2012; accepted June 30, 2012
Keywords: Matter Waves; Quantum Vacuum; De Broglie Waves; Special Relativity Theory; Inertia; Mach’s Principle
ABSTRACT
A new approach of the matter waves concept initiated by Louis de Broglie leads to a new model—the vacuum matter waves. By using the physics of time dilation, one can calculate a gravitational cutoff frequency, with respect to the spectrum of vacuum fluctuations, which is the upper bound of the frequency range of this new model. We described the properties of these new waves and outlined the connection between them and the dimensions at Planck length level. The calculation of velocity in circular orbits by using this new concept complies with the well-known equation. One of its consequences is that the structure of the physical vacuum is modified on the radial direction with the gravity source, but not modified on its tangential direction. This study places the space-time structure from sub-quantum level into a new light and makes the connection between this level and that of the planetary systems.
1. Introduction
In 1924, Louis de Broglie in his doctoral thesis “On the Theory of Quanta” [1], claimed the existence of matter waves and formulated the equation that carries his name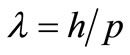 . This hypothesis says that particles of matter have wave-like properties. The concept of matter waves was experimentally confirmed for the first time in 1927 at Bell Labs, by Clinton Davisson and Lester Germer, by using electrons [2]. Recent experiments confirmed the de Broglie equation even for large molecules and macromolecules [3,4].
. This hypothesis says that particles of matter have wave-like properties. The concept of matter waves was experimentally confirmed for the first time in 1927 at Bell Labs, by Clinton Davisson and Lester Germer, by using electrons [2]. Recent experiments confirmed the de Broglie equation even for large molecules and macromolecules [3,4].
On the other hand, the tendency in modern physics, in an effort to unify the fundamental theories, is to find a connection between them and the quantum vacuum. This is the aim of this paper, namely to find out how this vacuum and the concept of matter waves are related.
The current study is grounded in the basic ideas of de Broglie, but using a new approach. Thus we are led to a new concept—vacuum matter waves—having a deterministic role in the genesis and motion of matter.
2. Vacuum Matter Waves
In modern physics, the concept of time dilation is a welldocumented physical phenomenon in both theory and experiments. This concept originates in the experiments for ether detection (luminiferous ether), which were initiated in 1887 by Albert Michelson and Edward Morley [5] and continued until recently with the use of lasers and high accuracy devices [6]. The Principle of Invariant Light Speed used by Einstein in his Special Relativity (SR), motivated by Maxwell’s theory of electromagnetism and the lack of evidence for luminiferous ether has as consequences time dilation and length contraction. Velocity and gravitational time dilation have been experimentally confirmed a number of times [7-12].
As is well known in SR, if the clock has a frequency 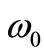 (angular frequency) in the rest frame of the particle, its frequency, according to the so-called time dilation, when it is moving with velocity
(angular frequency) in the rest frame of the particle, its frequency, according to the so-called time dilation, when it is moving with velocity 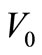 is:
is:
 (1)
(1)
where c0 denotes the speed of light in a vacuum in the absence of a gravitational field. De Broglie assumed that  is not the frequency of a clock moving with the particle, but the frequency of a wave accompanying the particle, propagating with velocity
is not the frequency of a clock moving with the particle, but the frequency of a wave accompanying the particle, propagating with velocity 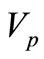 (phase velocity) in the direction of motion (suppose we simplify our 3-dimensional universe to a 1-dimensional universe where we also put in an x-axis). Moreover, in this study we will consider
(phase velocity) in the direction of motion (suppose we simplify our 3-dimensional universe to a 1-dimensional universe where we also put in an x-axis). Moreover, in this study we will consider 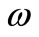 as a frequency from the spectrum of vacuum fluctuations. Equation (1) can be rewritten as follows:
as a frequency from the spectrum of vacuum fluctuations. Equation (1) can be rewritten as follows:
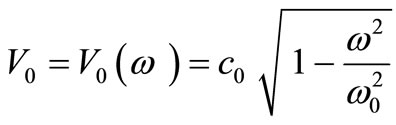 (2)
(2)
Also according to de Broglie’s theory, velocity 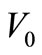 is the group velocity of a wave packet composed of plane waves of a narrow bandwidth. The relation between phase velocity
is the group velocity of a wave packet composed of plane waves of a narrow bandwidth. The relation between phase velocity  and group velocity
and group velocity 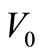 is given in the Rayleigh equation:
is given in the Rayleigh equation:
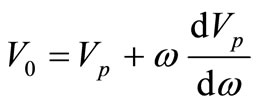 (3)
(3)
From Equations (2) and (3) results the following differential equation:
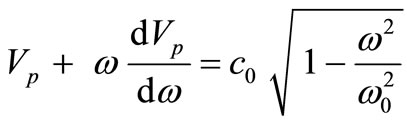 (4)
(4)
The solution of this equation is:
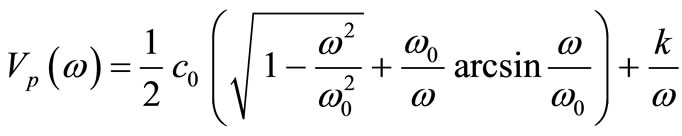 (5)
(5)
For avoiding an infinite value, but also for satisfying equation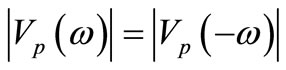 , we shall consider the solution for which
, we shall consider the solution for which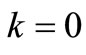 . For inserting the influence of the gravitational field in the Equation (5), we shall analyze the relativistic fall (Figure 1) of a massive particle with mass m in a static gravitational potential
. For inserting the influence of the gravitational field in the Equation (5), we shall analyze the relativistic fall (Figure 1) of a massive particle with mass m in a static gravitational potential 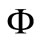 generated by mass
generated by mass .
.
This particle comes from an infinite distance ( ) with initial velocity
) with initial velocity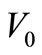 . Taking into account the gravitational potential
. Taking into account the gravitational potential , the relativistic velocity satisfies the following equation:
, the relativistic velocity satisfies the following equation:
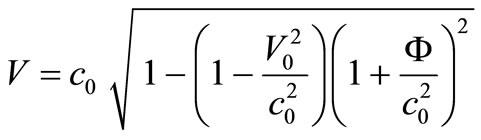 (6)
(6)
For the multibody potential, 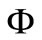 represents the sum of the Newtonian gravitational potentials due to the masses in the neighborhood.
represents the sum of the Newtonian gravitational potentials due to the masses in the neighborhood.
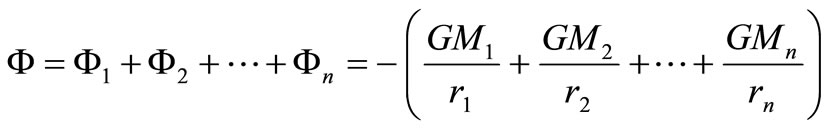 (7)
(7)
If considering Equation (1), Equation (6) is written as follows:
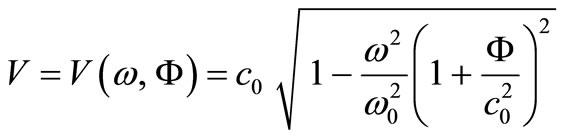 (8)
(8)
This equation can be rewritten in a simplified form as follows:
 (9)
(9)
in which we made the following denotation:
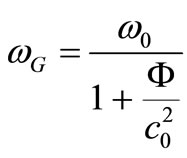 (10)
(10)
where 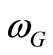 is the frequency from the spectrum of vacuum fluctuations, in which the group velocity is null.
is the frequency from the spectrum of vacuum fluctuations, in which the group velocity is null.
The phase velocity can likewise be computed in the way we obtained Equation (5):
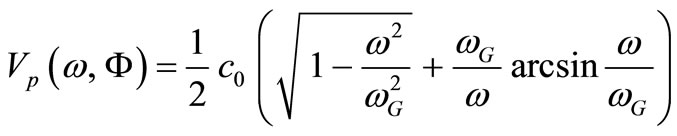 (11)
(11)
As can be seen in Figure 2, the range of frequencies 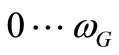 does cover the entire range that is necessary for generating the group velocities
does cover the entire range that is necessary for generating the group velocities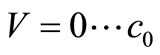 .
.
The value 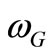 can be interpreted as a gravitational cutoff frequency, so that frequencies spectrum of vacuum fluctuations that may participate in the formation of the massive particles are in the range
can be interpreted as a gravitational cutoff frequency, so that frequencies spectrum of vacuum fluctuations that may participate in the formation of the massive particles are in the range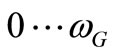 . Observe that as gravitational field strength is higher so the cutoff frequency is higher. We can interpret this fact as under the influence of gravity, a part of the frequency spectrum that is present in vacuum fluctuations is extracted and used in the genesis and motion of the matter. In the absence of gravity, the cutoff frequency has an initial value
. Observe that as gravitational field strength is higher so the cutoff frequency is higher. We can interpret this fact as under the influence of gravity, a part of the frequency spectrum that is present in vacuum fluctuations is extracted and used in the genesis and motion of the matter. In the absence of gravity, the cutoff frequency has an initial value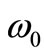 . Further, we call these waves having the phase velocity
. Further, we call these waves having the phase velocity 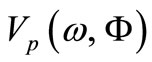 and frequencies in the range of
and frequencies in the range of 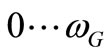 as vacuum matter waves.
as vacuum matter waves.
3. Properties of Vacuum Matter Waves
We can split the range of frequencies  by the value of the group velocity V relative to the escape velocity
by the value of the group velocity V relative to the escape velocity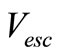 . Thus, for a frequency
. Thus, for a frequency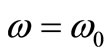 , the group velocity is equal to the escape velocity. For the range of frequencies lower than
, the group velocity is equal to the escape velocity. For the range of frequencies lower than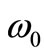 , the group velocity is higher than the escape velocity, while for the range of
, the group velocity is higher than the escape velocity, while for the range of  the group velocity is lower than the escape velocity.
the group velocity is lower than the escape velocity.

Figure 1. Relativistic fall in a static gravitational potential.
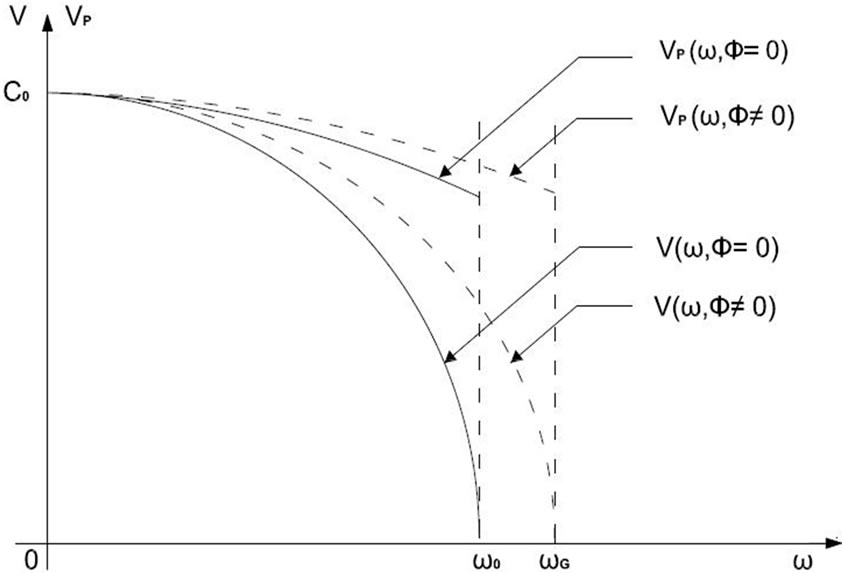
Figure 2. Phase (Vp) and group (V) velocities versus frequency (ω) and gravitational potential (Φ).
 (12)
(12)
For vacuum matter waves, the upper limit of the phase velocity is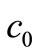 , and this holds for relatively low frequencies:
, and this holds for relatively low frequencies:
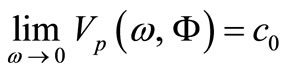 (13)
(13)
We can also observe that for a null group velocity, the phase velocity has a fixed value regardless of the of the gravitational field strength:
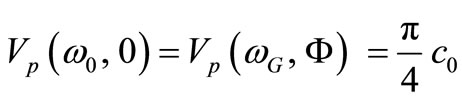 (14)
(14)
De Broglie-Einstein velocity equation (an equivalent equation) is:
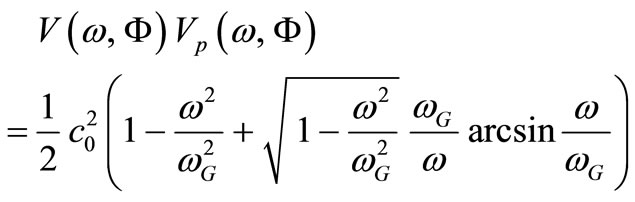 (15)
(15)
and has the following property:
 (16)
(16)
In a static gravitational field the refractive index 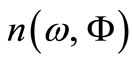 for vacuum matter waves is:
for vacuum matter waves is:
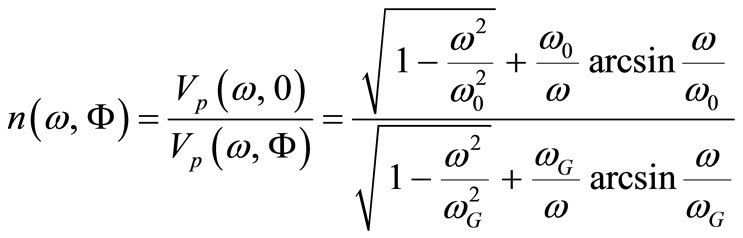 (17)
(17)
The graphical form (Figure 2) of the phase velocity 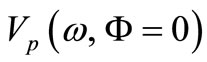 around the gravitational cutoff frequency
around the gravitational cutoff frequency 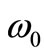 suggests that there exists a minimal value of the wavelength
suggests that there exists a minimal value of the wavelength 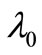 for which vacuum matter waves do exist. Thus, we can deduce a value for
for which vacuum matter waves do exist. Thus, we can deduce a value for  from the following equation:
from the following equation:
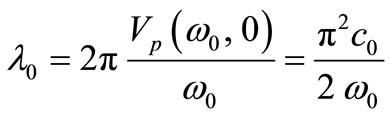 (18)
(18)
 (19)
(19)
Equations (10) and (14) yield the minimal value of the wavelength 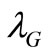 as a function of the gravitational potential:
as a function of the gravitational potential:
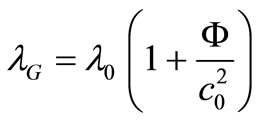 (20)
(20)
From this equation, it follows that the gravitational potential “deforms” the structure of the physical vacuum, leading to a minimal wavelength . The vacuum matter waves do not exist below this value.
. The vacuum matter waves do not exist below this value.
We could speculate that 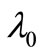 has the Planck length, defined as:
has the Planck length, defined as:
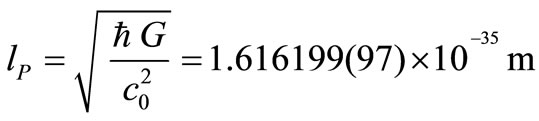 (21)
(21)
In this case, we can compute the initial value of the cutoff frequency by using Equation (19):
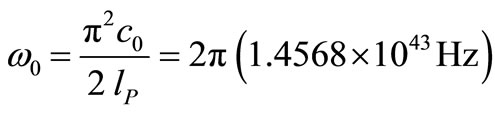 (22)
(22)
A brief characterization of the vacuum matter waves in a 1-dimensional universe can be done through the following equations (see Table 1).


Table 1. Vacuum matter waves properties.
4. Escape Velocity
For the escape velocity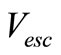 , the wave packet is centered on frequency
, the wave packet is centered on frequency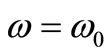 . The value of this velocity can be computed through Equation (8) as follows:
. The value of this velocity can be computed through Equation (8) as follows:
 (23)
(23)
5. Circular Orbit Velocity
Denote by 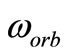 the central frequency of a wave packet moving on a circular orbit with velocity
the central frequency of a wave packet moving on a circular orbit with velocity
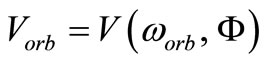 .
.
The wavelength of vacuum matter waves corresponding to this frequency is:
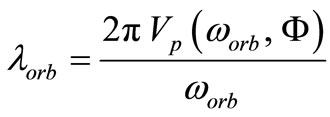 (24)
(24)
We impose the condition of stability of the circular orbit,
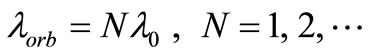 (25)
(25)
which leads us to the following equation:
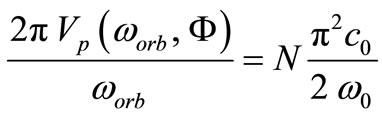 (26)
(26)
This equation can be solved by means of approximate methods using mathematical software. For 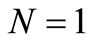 and
and , one of these approximated solutions is:
, one of these approximated solutions is:
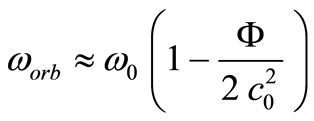 (27)
(27)
We can compute the circular orbit velocity by using Equation (8):
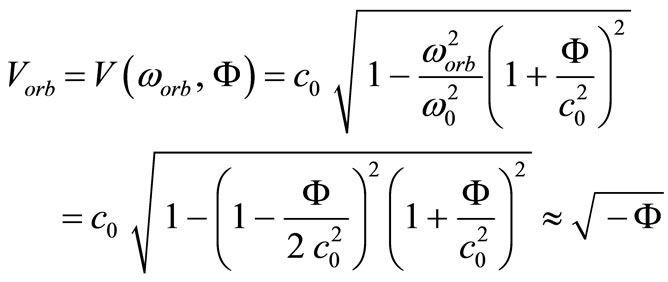 (28)
(28)
that is the well-known nonrelativistic value of this velocity. Obtaining the equation of the orbital velocity is of the utmost importance, because it confirms this study.
The stability condition (25) has been considered as a necessity of a synchronism between the wavelength  corresponding to the velocity of the motion and the wavelength
corresponding to the velocity of the motion and the wavelength 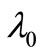 characterizing the physical vacuum. A consequence of obeying this condition is the fact that the gravitational potential “deforms” the physical vacuum on the radial direction with the gravity source, but not on its tangential direction.
characterizing the physical vacuum. A consequence of obeying this condition is the fact that the gravitational potential “deforms” the physical vacuum on the radial direction with the gravity source, but not on its tangential direction.
6. Inertia and Gravity: The Same Phenomenon
The similarity between (2) and (9) and also between (5) and (11) suggests the fact that as gravitational cutoff frequency 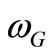 is generated by a gravitational potential
is generated by a gravitational potential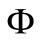 , so
, so 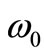 could be generated by a default gravitational potential
could be generated by a default gravitational potential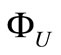 . Thus, the total gravitational potential has the following equation:
. Thus, the total gravitational potential has the following equation:
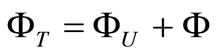 (29)
(29)
In this case, equation (10) is just an approximation of the cutoff frequency 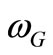 around the value
around the value  and we should find a function of the form:
and we should find a function of the form:
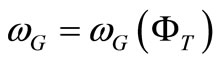 (30)
(30)
Gravitational potential  is generated by all the mass-energy in the entire universe and inertia depends on it [13]. To illustrate the above, in a simplified model, we consider that all mass-energy
is generated by all the mass-energy in the entire universe and inertia depends on it [13]. To illustrate the above, in a simplified model, we consider that all mass-energy 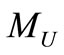 of the universe is distributed uniformly on a thin spherical shell of radius
of the universe is distributed uniformly on a thin spherical shell of radius 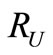 (Figure 3). Gravitational potential generated by the universe is constantly all the volume.
(Figure 3). Gravitational potential generated by the universe is constantly all the volume.
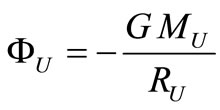 (31)
(31)
A mass M located inside the sphere generates a gravitational potential:
 (32)
(32)
Total gravitational potential inside the sphere is:
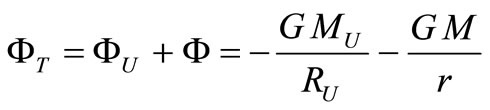 (33)
(33)
If we define the space  inside the sphere, a test mass m located in a certain place into this space will have a well-defined velocity. In other words, the particle velocity, which is given by the group velocity
inside the sphere, a test mass m located in a certain place into this space will have a well-defined velocity. In other words, the particle velocity, which is given by the group velocity
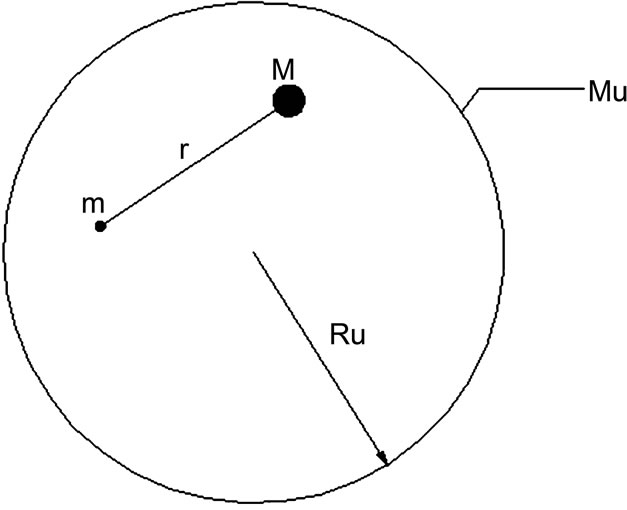
Figure 3. The universe as a thin spherical shell.
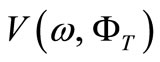 is a property of the space but not the test mass. In this space if
is a property of the space but not the test mass. In this space if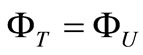 , the motion of the test mass is inertial
, the motion of the test mass is inertial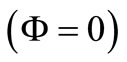 . If
. If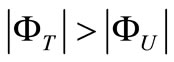 , the motion is produced under the influence of an supplementary gravitational potential
, the motion is produced under the influence of an supplementary gravitational potential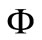 . We conclude that in this space, the group velocity
. We conclude that in this space, the group velocity 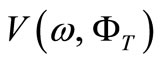 depends on a unique gravitational potential
depends on a unique gravitational potential 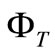 does not distinguish between inertial motion and a motion near a mass M.
does not distinguish between inertial motion and a motion near a mass M.
 (34)
(34)
From this point of view, inertia and gravitation are the same phenomenon.
7. Compton Frequency and De Broglie Equation
The nature of the Compton frequency must be the same as the vacuum matter waves. It would be complicated to consider that it would have another origin. One of the possibilities is that Compton frequency 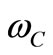 be given by a narrow bandwidth
be given by a narrow bandwidth 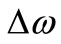 of a wave packet, centered on frequency
of a wave packet, centered on frequency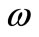 , with the following equation:
, with the following equation:
 (35)
(35)
Of course, 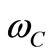 is the frequency you see in the reference frame of the particle. If the particle moves with velocity
is the frequency you see in the reference frame of the particle. If the particle moves with velocity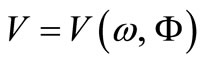 , then this frequency changes according to the value:
, then this frequency changes according to the value:
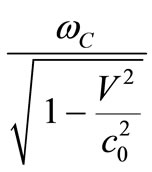 (36)
(36)
The associated wavelength is given by the de Broglie equation 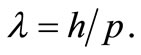 This way of interpreting the Compton frequency would also justify the equation of energy:
This way of interpreting the Compton frequency would also justify the equation of energy:
 (37)
(37)
given that the energy of a harmonic oscillator is proportional to the square of its frequency.
8. Conclusions
Using a new approach of the matter waves concept initiated by Louis de Broglie we have build a new model— the vacuum matter waves. For this new model we have calculated the upper limit of the frequency spectrum (gravitational cutoff frequency) as well as some properties. This allows us to get the following conclusions:
- there is a close deterministic (non probabilistic) relationship between matter, vacuum matter waves and quantum vacuum;
- there is a gravitational cutoff frequency regarding vacuum fluctuations;
- this new model makes the connection between Planck level and that of the planetary systems;
- the space-time is not continuous but discrete;
- inertia and gravity are the same phenomenon.
REFERENCES
- L. De Broglie, “On the Theory of Quanta,” English translation by A. F. Kracklauer, Annales Fondation Louis de Broglie, 2004.
- C. Davisson and L. H. Germer, “The Scattering of Electrons by a Single Crystal of Nickel,” Nature, Vol. 119, 1927, pp. 558-560. doi:10.1038/119558a0
- M. Arndt, O. Nairz, J. Voss-Andreae, C. Keller, G. van der Zouw and A. Zeilinger, “Wave-particle duality of C60 molecules,” Nature, Vol. 401, 1999, pp. 680-682. doi:10.1038/44348
- S. Gerlich, S. Eibenberger, M. Tomandl, S. Nimmrichter, K. Hornberger, P. J. Fagan, J. Tüxen, M. Mayor and M. Arndt, “Quantum interference of Large Organic Molecules,” Nature Communications, Vol. 2, No. 263, 2011, Article ID: 263. doi:10.1038/ncomms1263
- A. A. Michelson and E. W. Morley, “On the Relative Motion of the Earth and the Luminiferous Ether,” American Journal of Science, Vol. 34, No. 203, 1887, pp. 333- 345.
- H. Muller, et al., “Modern Michelson-Morley Experiment Using Cryogenic Optical Resonators,” 2003. http://arxiv.org/abs/physics/0305117
- H. E. Ives and G. R. Stilwell, “An Experimental Study of the rate of a moving clock,” Journal of the Optical Society of America, Vol. 28, 1938, pp. 215-226. doi:10.1364/JOSA.28.000215
- H. E. Ives and G. R. Stilwell, “An experimental study of the rate of a moving clock,” Journal of the Optical Society of America, Vol. 31, 1941, pp. 369-374. doi:10.1364/JOSA.31.000369
- B. Rossi and D. B. Hall, “Variation of the Rate of Decay of Mesotrons with Momentum,” Physical Review, Vol. 59, No. 3, 1941, pp. 223-229. doi:10.1103/PhysRev.59.223
- C. W. Chou, D. B. Hume, T. Rosenband and D. J. Wineland, “Optical Clocks and Relativity,” Science, Vol. 329 No. 5999, 2010, pp. 1630-1633. doi:10.1126/science.1192720
- R. V. Pound and G. A. Rebka Jr., “Gravitational RedShift in Nuclear Resonance,” Physical Review Letters, Vol. 3 No. 9, 1959, pp. 439-441. doi:10.1103/PhysRevLett.3.439
- J. Hafele and R. Keating, “Around the World Atomic Clocks: Predicted Relativistic Time Gains,” Science, Vol. 177, No. 4044, 1972, pp. 166-168. doi:10.1126/science.177.4044.166
- D. W. Sciama, “The physical foundations of general relativity,” Heinemann Educational Books Ltd., London, 1969.

