Journal of Modern Physics
Vol.3 No.1(2012), Article ID:17105,5 pages DOI:10.4236/jmp.2012.31012
Simple Landau Model of the Liquid-RII-RI Rotator Phases of Alkanes
Department of Physics, Presidency University, 86/1, College Street, Kolkata-700073, India
Email: *pkmuk1966@gmail.com
Received October 15, 2011; revised December 16, 2011; accepted December 29, 2011
Keywords: rotator phases; phase transitions; Landau theory
ABSTRACT
Simple Landau free energy function is presented to describe the Liquid-RII-RI phase sequence of alkanes and transitions between them. The order parameters necessary to describe these rotator phase transitions are identified. We present a mean-field description of the Liquid-RII and Liquid-RI transitions. General arguments are presented for the topology of the phase diagram in the vicinity of the Liquid-RII-RI triple point. Within this model the Liquid-RII and Liquid-RI transitions are found to be always strongly first order. Calculations based on this model agree qualitatively with experiments.
1. Introduction
During the last two decades much progress has taken place in the field of rotator phases. Rotator phases are among the most interesting condensed states of matter exhibited by normal alkanes (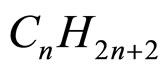 ), alcohols, and other hydrocarbon chain systems consisting of layered structures with three dimensional crystalline order of the center of mass, but no long range orientational order of the molecules about their long axes. Rotator phases have a number of unique and unusual properties which include surface crystallization, anomalous heat capacity, negative thermal compressibilities and unusually high thermal expansions. Five different rotator phases had been identified. The rotator-II (
), alcohols, and other hydrocarbon chain systems consisting of layered structures with three dimensional crystalline order of the center of mass, but no long range orientational order of the molecules about their long axes. Rotator phases have a number of unique and unusual properties which include surface crystallization, anomalous heat capacity, negative thermal compressibilities and unusually high thermal expansions. Five different rotator phases had been identified. The rotator-II ( ) phase is usually described as composed of molecules that are untilted with respect to the layers that are packed in a hexagonal lattice. The layers are stacked in an ABCABC... trilayer stacking sequence. This phase is also referred to as the rhombohedral phase. In the rotator-I (
) phase is usually described as composed of molecules that are untilted with respect to the layers that are packed in a hexagonal lattice. The layers are stacked in an ABCABC... trilayer stacking sequence. This phase is also referred to as the rhombohedral phase. In the rotator-I ( ) phase the molecules are also untilted with respect to the layers and there is a rectangularly distorted hexagonal lattice. The layers are stacked in an ABAB... bilayer stacking sequence. This phase is referred to as the face-centered-orthorhombic (FCO) phase. In shorter chain lengths the phase sequence was reported to be Liquid-RII-RI-Crystal.
) phase the molecules are also untilted with respect to the layers and there is a rectangularly distorted hexagonal lattice. The layers are stacked in an ABAB... bilayer stacking sequence. This phase is referred to as the face-centered-orthorhombic (FCO) phase. In shorter chain lengths the phase sequence was reported to be Liquid-RII-RI-Crystal.
A large number of experimental studies [1-10] are devoted to describe the structure and the phase transitions of the rotator phases. According to the X-ray scattering study by Sirota et al. [3], the RII-RI transition is first order with jump of the distortion order parameter and sharp peak on the heat capacity data [4]. The binary mixtures of normal alkanes [11-14] also shows a first order character of the RII-RI transition. Sirota et al. [15] carried out a high pressure study on the RII-RI transition and confirmed the first order character of the RII-RI transition. Zammit et al. [7,8] studied the IL-RII and RII-RI transitions in pure and binary mixtures of alkanes. Over the IL-RII transition, they observed the single peak in both the specific heat and latent heat in the pure material, splits into two features at different temperatures. This indicates the first order character of the IL-RII transition. They also confirmed the first order character of the RII-RI transitions. The presence of the thermal hysteresis at these transitions indicates the first order character of the transition.
Theoretical studies of the RII-RI transition follow two main lines. The first approach consists of Monte Carlo and molecular dynamics simulations [16-22] which confirms the first order character of the Liquid-RII (IL-RII) and RII-RI transitions. The second approach is pursued by Wurger [23] and Mukherjee [24-34]. Wurger [23] developed a microscopic model for the pair interaction of hydrocarbon chains and discussed the detailed structure of the RI and RII phases in terms of a molecular-field approximation. In a series of paper Mukherjee [24-26] discussed RII-RI phase transition within Landau phenomenological approach and discussed in detail the various aspect of this transition including the elastic properties.
To the best of the author’s knowledge, there is so far no detailed theoretical studies on the IL-RII-RI phase sequence and the transitions between them. The purpose of the present paper is to investigate the IL-RII-RI phase sequence and the transitions between them within Landau theory. We define a new order parameter to describe the IL-RII and IL-RI phase transitions.
2. Model
Order Parameters
The RI phase differs from the RII phase only in the distortion of the hexagonal lattice. Following [5,35] we define the lattice distortion parameter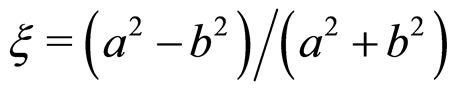 where a and b are the major and minor axes of an ellipse draws through the six nearest neighbors. The distortion
where a and b are the major and minor axes of an ellipse draws through the six nearest neighbors. The distortion 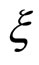 is defined with respect to a plane whose normal is parallel to the long molecular axes.
is defined with respect to a plane whose normal is parallel to the long molecular axes.  for the RII phase. Thus we take
for the RII phase. Thus we take 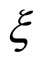 as an order parameter for the RII-RI transition.
as an order parameter for the RII-RI transition.
Now to define the order parameter of the IL-RII or IL-RI transitions. The low temperature crystal phase of n-alkanes is found to exist in layered structures. In these cases the molecules stay in some layer stacking and the probability that a single molecule is present (partially) in two simultaneous layers is almost zero. When the temperature rises further the stacking breaks, i.e. the molecules start occupying positions which are shared by more than one layer stacking. We may choose to represent alternate layer sequences with suffixes  etc. The bilayer stacking can be represented as
etc. The bilayer stacking can be represented as 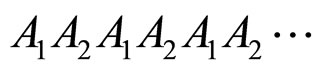 and the trilayer stacking can be represented as
and the trilayer stacking can be represented as 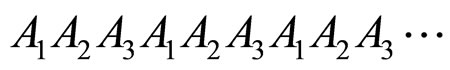 We represent the probability of the k-th molecule of the system to occupy any of the j-th layer sequence as
We represent the probability of the k-th molecule of the system to occupy any of the j-th layer sequence as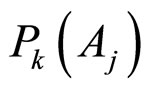 . For bilayer the only feasible cases are
. For bilayer the only feasible cases are 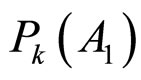 and
and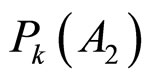 , one of which is 1 and the other being 0 in perfect layer ordering. Now we define a correlation factor
, one of which is 1 and the other being 0 in perfect layer ordering. Now we define a correlation factor 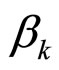 for the k-th molecule in a N-layer stacking as
for the k-th molecule in a N-layer stacking as
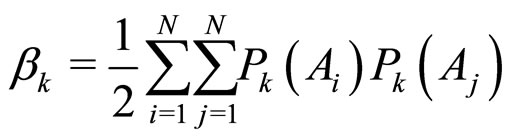 (1)
(1)
This is clearly 0 in ordered layer phase and non-zero in other phases with lower or higher order.
The rotator phases of n-alkanes are found to exist in bilayer and trilayer structures. If we consider the correlation factor for the highest possible layer structure in the alkanes, i.e. trilayer we find that for the k-th molecule
 (2)
(2)
It is 0 (or almost zero) in RII and RI phases which in nature are bilayer and trilayer respectively. 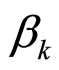 does have a finite value in the liquid phase which can be calculated. In isotropic liquid phase the probability density of the k-th molecule is constant everywhere in space. So,
does have a finite value in the liquid phase which can be calculated. In isotropic liquid phase the probability density of the k-th molecule is constant everywhere in space. So,
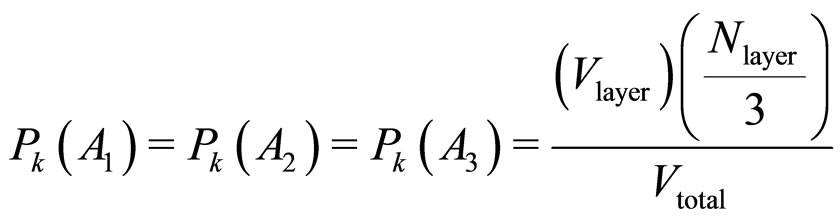 ,
,
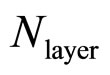 is the total number of layers. Hence
is the total number of layers. Hence 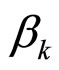 can be expressed as
can be expressed as
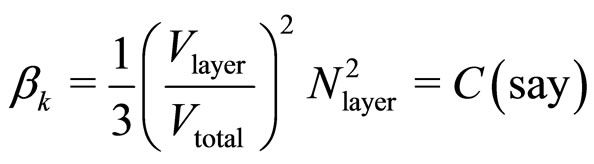 (3)
(3)
Thus  is independent of k. Hence we define the correlation order parameter
is independent of k. Hence we define the correlation order parameter  as
as
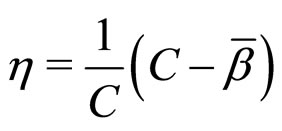 (4)
(4)
Here the average correlation factor is calculated for all molecules together.
Thus  is 0 is the isotropic liquid phase and has a value >0 in the RI and RII phases.
is 0 is the isotropic liquid phase and has a value >0 in the RI and RII phases.
3. Free Energy
Thus we take  and
and 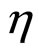 as two order parameters involved in the RI-RII, IL-RII and IL-RI phase transitions. For simplicity we neglect the weak interlayer interaction between the stacking layers in different rotator phases so that the problem becomes two dimensional. The distortion is a two component order parameter; its components are expressed the distortion amplitude
as two order parameters involved in the RI-RII, IL-RII and IL-RI phase transitions. For simplicity we neglect the weak interlayer interaction between the stacking layers in different rotator phases so that the problem becomes two dimensional. The distortion is a two component order parameter; its components are expressed the distortion amplitude 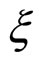 and the azimuthal angle
and the azimuthal angle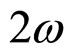 . The multiplier 2 comes from the fact that the distortion is a symmetric traceless tensor. Since the the free energy is a scalar quantity, negative and positive
. The multiplier 2 comes from the fact that the distortion is a symmetric traceless tensor. Since the the free energy is a scalar quantity, negative and positive  and
and  result in inequivalent structures, causing the Landau free energy expansion contain
result in inequivalent structures, causing the Landau free energy expansion contain 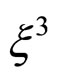 and
and 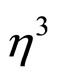 terms, thus resulting in a first order transition. Expanding the total free energy in terms of the above mentioned order parameters yields
terms, thus resulting in a first order transition. Expanding the total free energy in terms of the above mentioned order parameters yields
 (5)
(5)
where 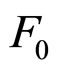 is free energy of the isotropic liquid phase. The coefficients a and
is free energy of the isotropic liquid phase. The coefficients a and  are assumed to vary strongly with an external parameter. For
are assumed to vary strongly with an external parameter. For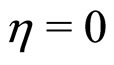 , free energy (5) describe a first order RI-RII transition for b > 0 and c > 0. In this case the minimum free energy occurs at
, free energy (5) describe a first order RI-RII transition for b > 0 and c > 0. In this case the minimum free energy occurs at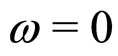 , for b > 0 and at
, for b > 0 and at 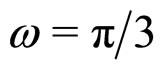 for b < 0. According to the experimental observations, in the RI phase,
for b < 0. According to the experimental observations, in the RI phase,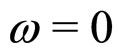 . H is the coupling constant.
. H is the coupling constant.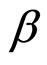 ,
, 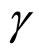 , b, c and H are chosen positive.
, b, c and H are chosen positive.
The material parameters a and 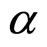 can be assumed as
can be assumed as 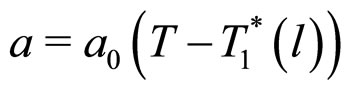 and
and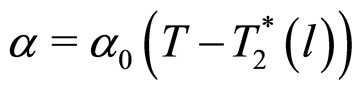 .
. 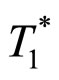 and
and 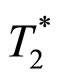 are virtual transition temperatures.
are virtual transition temperatures.  and
and 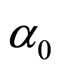 are constants.
are constants.
From the experimental phase diagrams [3] one observes, 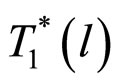 and
and  can be portrayed as
can be portrayed as
 and
and where
where  is some specific chain length of the molecules. u and v are positive constants.
is some specific chain length of the molecules. u and v are positive constants.
Minimization of Equation (5) with respect to  and
and 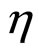 yields the following phases:
yields the following phases:
1) Isotropic liquid (IL) phase: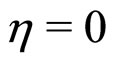 ,
,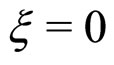 .
.
This phase exists for 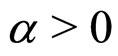 and a > 0.
and a > 0.
2) RII phase: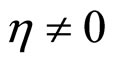 ,
,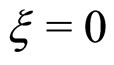 .
.
The RII phase exists when  and a > 0.
and a > 0.
3) RI phase: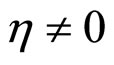 ,
,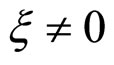 .
.
The RI phase exists for 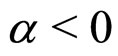 and a < 0.
and a < 0.
Thus it is clear from the solutions that three types of transition are possible: 1) IL-RII; 2) IL-RI; 3) RII-RI.
The sufficient condition for the RI phase to be stable are
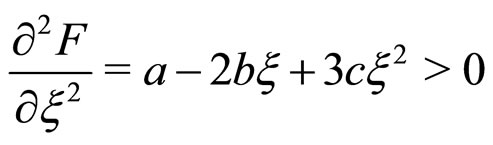 (6)
(6)
 (7)
(7)
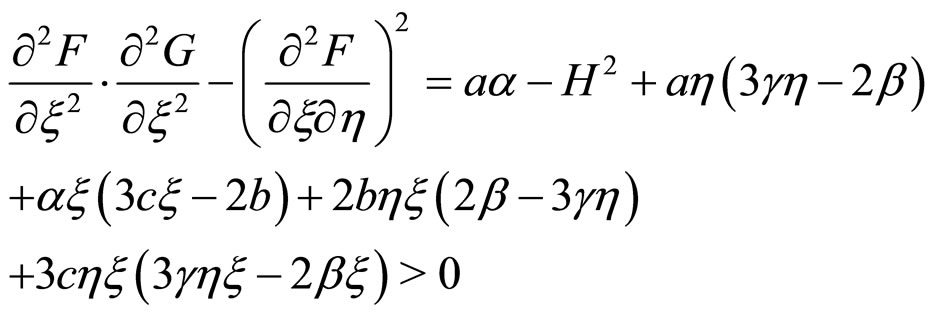 (8)
(8)
These three conditions determine the stability of the RI phase explicitly. The sufficient condition for the stability of the RII phase reads
 (9)
(9)
For the IL phase the stability conditions are 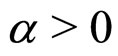 and a > 0.
and a > 0.
By lowering the temperature from the isotropic liquid phase, the RII and RI phases can appear sequentially or in partial sequence. The RII and RI phases can arise either directly from the IL phase along the curves IL-RII and IL-RI or along the curve RII-RI. In the spirit of Landau theory all the phase transitions IL-RII, IL-RI and RII-RI are first order because of the cubic invariant in the free energy expansion. If all the phase transitions involved are first order ones, then one can observe the IL-RII-RI triple point as observed in experiment [3].
The conditions for the first order RII-RI transition can be obtained as
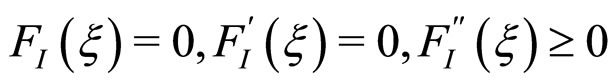 (10)
(10)
The conditions for the first order IL-RI transition are given by
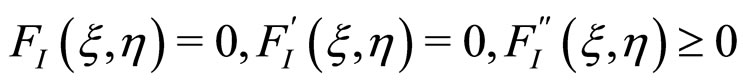 (11)
(11)
The conditions for the first order IL-RII transition read
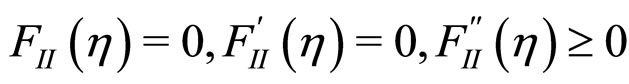 (12)
(12)
Solving (10)-(12) simultaneously will determine the various phase transition lines. Figure 1 shows a typical phase diagram for the IL-RI, IL-RII and RII-RI phase transitions. As can be seen from the Figure 1, the RII and RI phases arise from the isotropic phase along the curves IL-RII and IL-RI or along the curve RII-RI respectively. The IL-RII and IL-RI transitions are first order because of the cubic invariant in the free energy expansion. The line of the RII-RI transition starts at the IL-RII-RI triple point as shown in Figure 1. When the temperature of the IL-RII and of RII-RI transitions coincide, a triple point appears.
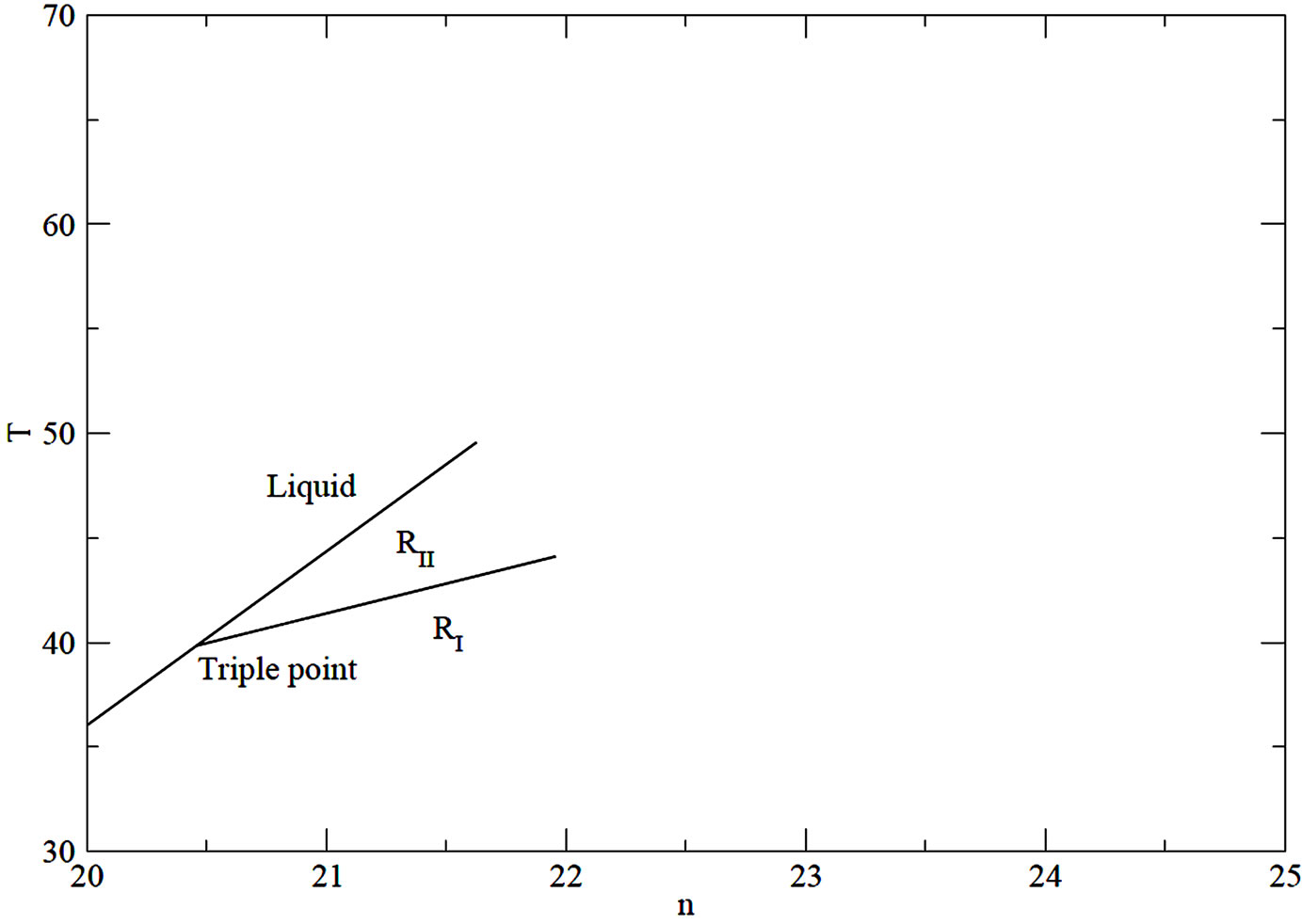
Figure 1. Possible chain length (n)-temperature (T) phase diagram in the vicinity of the Liquid-RII-RI triple point.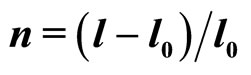 .
.
The region of the RI phase shrinks and finally disappears when the IL-RII transition takes place. In experimental studies [3], alkanes C20-C27 show such a IL-RII transition via triple point. Thus the above analysis of the IL-RII-RI triple point agrees well with the experimental observations [3]. Thus there is always a direct IL-RII transition is possible within the framework of our model free energy (6) satisfying the above stability conditions. Of course the IL-RI transition could proceed before the IL-RII the transition temperature 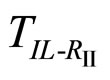 is reached. To prevent this,
is reached. To prevent this, 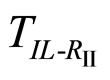 has to be larger than the IL-RI transition temperature
has to be larger than the IL-RI transition temperature 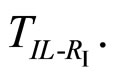 Thus we have always
Thus we have always 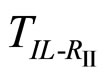
 . The cubic coefficient
. The cubic coefficient 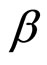 in the free energy (5) yields a first order IL-RII transition at
in the free energy (5) yields a first order IL-RII transition at
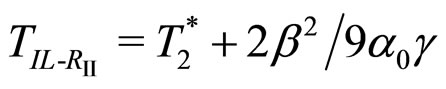
with an order parameter jump 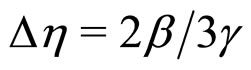 and a latent heat of
and a latent heat of . The so-called temperature hysteresis is related to the existence of metastable states within a certain temperature range. The above analysis qualitatively agrees with experimental observations[3,4,7,8].
. The so-called temperature hysteresis is related to the existence of metastable states within a certain temperature range. The above analysis qualitatively agrees with experimental observations[3,4,7,8].
4. Conclusion
A simple model free energy has been constructed to describe the IL-RII-RI phase sequence and transitions between them. The order parameters are identified for different phase transitions. The model predicts the first order character of the IL-RII, IL-RI and RII-RI transitions and IL-RII-RI triple point in the 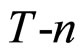 phase diagram. The proposed interpretation of the IL-RII transition allow us to explain the various types of phase behavior observed experimentally. These results are in qualitative agreement with all experiments reported so far.
phase diagram. The proposed interpretation of the IL-RII transition allow us to explain the various types of phase behavior observed experimentally. These results are in qualitative agreement with all experiments reported so far.
5. Acknowledgements
PKM thanks the Alexander von Humboldt Foundation for equipment and book grant.
REFERENCES
- J. Doucet, I. Denicolo and A. Craievich, “X-Ray Study of the Rotator Phase of the Odd-Numbered Paraffins C17H36, C19H40, and C21H44,” Journal of Chemical Physics, Vol. 75, No. 3, 1981, pp. 1523-1529. doi:10.1063/1.442185
- U. Ungar and N. Masic, “Order in the Rotator Phase of n-Alkanes,” The Journal of Physical Chemistry, Vol. 89, No. 6, 1985, pp. 1036-1042. doi:10.1021/j100252a030
- E. B. Sirota, H. E. King Jr., D. M. Singer and H. H. Shao, “Rotator Phases of the Normal Alkanes: An X-Ray Scattering Study,” Journal of Chemical Physics, Vol. 98, No. 7, 1993, pp. 5809-5824. doi:10.1063/1.464874
- E. B. Sirota and D. M. Singer, “Phase Transitions among the Rotator Phases of the Normal Alkanes,” Journal of Chemical Physics, Vol. 101, No. 12, 1994, pp. 10873- 10882. doi:10.1063/1.467837
- E. B. Sirota, “Remarks Concerning the Relation between Rotator Phases of Bulk n-Alkanes and Those of Langmuir Monolayers of Alkyl-Chain Surfactant on Water,” Langmuir, Vol. 13, No. 14, 1997, pp. 3849-3859. doi:10.1021/la9702291
- M. V. Kumar, S. K. Prasad and D. S. S. Rao, “Confinement Driven Weakening of the Rotator Phase Transitions in an Alkane through a Possible Tricritical Point,” Langmuir, Vol. 26, No. 23, 2010, pp. 18362-18368. doi:10.1021/la1037266
- U. Zammit, M. Marinelli and F. Mercuri, “Analysis of the Order Character of the RIIRI and the RIRV Rotator Phase Transitions in Alkanes by Photopyroelectric Calorimetry,” The Journal of Physical Chemistry B, Vol. 114, No. 24, 2010, pp. 8134-8139. doi:10.1021/jp102609y
- U. Zammit, M. Marinelli, F. Mercuri and F. Scudieri, “Effect of Quenched Disorder on the RI-RV, RII-RI and Liquid-RII Rotator Phase Transition in Alkanes,” The Journal of Physical Chemistry B, Vol. 115, No. 10, 2011, pp. 2331-2337. doi:10.1021/jp111067z
- H. Rensmo, A. Ongaro, D. Ryam and D. Fitzmaurice, “Self-Assembly of Alkane Capped Silver and Silica Nanoparticles,” Journal of Materials Chemistry, Vol. 12, No. 9, 2002, pp. 2762-2768. doi:10.1039/b204057c
- K. Jiang, B. Xia, D. Fu, F. Luo, G. Liu, Y. Su and D. Wang, “Solid-Solid Phase Transition of n-Alkanes in Multiple Nanoscale Confinement,” The Journal of Physical Chemistry B, Vol. 114, No. 3, 2010, pp. 1388-1392. doi:10.1021/jp9111475
- I. Denicolo, A. F. Craievich and J. Doucet, “X-Ray Diffraction and Calorimetric Phase Study of a Binary Paraffin: C23-C48-C24H50,” Journal of Chemical Physics, Vol. 80, No. 12, 1984, pp. 6200-6203. doi:10.1063/1.446722
- R. G. Snyder, G. Conti, H. L. Strauss and D. L. Dorset, “Termally-Induced Mixing in Partially Microphase Segregated Binary n-Alkane Crystals,” The Journal of Physical Chemistry, Vol. 97, No. 28, 1993, pp. 7342-7350. doi:10.1021/j100130a037
- E. B. Sirota, H. E. King Jr., G. J. Hughes and W. K. Wan, “Novel Phase Behavior in Normal Alkanes,” Physical Review Letters, Vol. 68, No. 4, 1992, pp. 492-495. doi:10.1103/PhysRevLett.68.492
- E. B. Sirota, H. E. King Jr., H. H. Shao and D. M. Singer, “Rotator Phases in Mixtures of n-Alkanes,” The Journal of Physical Chemistry, Vol. 99, No. 2, 1995, pp. 798-804. doi:10.1021/j100002a050
- E. B. Sirota, D. M. Singer and H. E. King Jr., “Structural Effects of High Pressure Gas on the Rotator Phases of Normal Alkanes,” Journal of Chemical Physics, Vol. 100, No. 2, 1994, pp. 1542-1551. doi:10.1063/1.466633
- J.-P. Ryckaert, I. R. McDonald and M. L. Klein, “Disorder in the Pseudohexagonal Rotator Phase of n-Alkanes: Molecular-Dynamics Calculations for Tricosane,” Molecular Physics, Vol. 67, No. 5, 1989, pp. 957-979. doi:10.1080/00268978900101561
- N. Wentzel and S. T. Milner, “Crystal and Rotator Phases of n-Alkanes: A Molecular Study,” Journal of Chemical Physics, Vol. 132, 2010, pp. 044901-(1-10).
- N. Wentzel and S. T. Milner, “Simulation of Multiple Ordered Phases in C23 N-Alkane,” Journal of Chemical Physics, Vol. 134, 2011, pp. 224504-(1-11).
- S. T. Milner and N. Wentzel, “Twist Solitons in Ordered Phases of n-Alkanes,” Soft Matter, Vol. 7, No. 16, 2011, pp. 7477-7492. doi:10.1039/c1sm05326d
- A. Marbeuf and R. J. Brown, “Molecular Dynamics in n-Alkanes: Premelting Phenomena and Rotator Phases,” Journal of Chemical Physics, Vol. 124, 2006, pp. 054901- (1-9).
- M. Cao and P. A. Monson, “Solid-Fluid and Solid-Solid Phase Equilibrium in a Model of n-Alkane Mixtures,” Journal of Chemical Physics, Vol. 120, No. 6, 2004, pp. 2980-2988. doi:10.1063/1.1637332
- M. Cao and P. H. Monson, “Solid-Fluid and Solid-Solid Equilibrium in Hard Sphere United Atom Models of n-Alkanes: Rotator Phase Stability,” The Journal of Physical Chemistry B, Vol. 113, No. 42, 2009, pp. 13866- 13873. doi:10.1021/jp902887w
- A. Würger, “Rotator Phases and Herringbone Order in Langmuir Monolayers and Alkanes,” Journal of Chemical Physics, Vol. 112, No. 8, 2000, pp. 3897-3908. doi:10.1063/1.480537
- P. K. Mukherjee and M. Deutsch, “Landau Theory of the RII-RI-RV Rotator Phases,” Physical Review B, Vol. 60, No. 5, 1999, pp. 3154-3162. doi:10.1103/PhysRevB.60.3154
- P. K. Mukherjee, “Rotator-I to Rotator-I Phase Transition in Alkanes,” Journal of Chemical Physics, Vol. 113, No. 10, 2000, pp. 4472-4475. doi:10.1063/1.1287422
- P. K. Mukherjee, “Elastic Properties of the Rotator Phases of Pentacosane C25H52,” Journal of Chemical Physics, Vol. 116, No. 24, 2002, pp. 10787-10793. doi:10.1063/1.1479711
- P. K. Mukherjee, “Structural Phase Transition in Pentacosane C25H52,” Journal of Chemical Physics, Vol. 126, 2007, pp. 114501-(1-7).
- P. K. Mukherjee, “Landau Model of the RII-RI-RV Rotator Phases in Mixtures of Alkanes,” Journal of Chemical Physics, Vol. 127, 2007, pp. 074901-(1-6).
- P. K. Mukherjee, “Simple Landau Model of the RIV- RIII-RV Rotator Phases of Alkanes,” Journal of Chemical Physics, Vol. 129, 2008, pp. 021101-(1-3).
- P. K. Mukherjee, “Pressure Effect on the Rotator-II to Rotator-I Transition of Alkanes,” Journal of Chemical Physics, Vol. 130, 2009, pp. 214906-(1-4).
- P. K. Mukherjee, “Tricritical Behavior of the Rotator Phases of Normal Alkanes,” The Journal of Physical Chemistry B, Vol. 114, No. 17, 2010, pp. 5700-5703. doi:10.1021/jp1000495
- P. K. Mukherjee, “Renormalization-Group Analysis of the RI-RV Rotator Phase Transition,” Journal of Chemical Physics, Vol. 134, 2011, pp. 224502-(1-6).
- P. K. Mukherjee, “Elastic Properties of the RIV-RIII Rotator Phases of Alkanes,” Journal of Physics and Chemistry of Solids, Vol. 102, 2011, pp. 1166-1169.
- P. K. Mukherjee, “Tricritical Behavior of the RI-RV Rotator Phase Transition in a Mixture of Alkanes with Nanoparticles,” Journal of Chemical Physics, Vol. 135, 2011, pp. 134505-(1-6).
- V. M. Kaganer, H. Möhwald and P. Dutta, “Structure and Phase Transitions in Langmuir Monolayers,” Reviews of Modern Physics, Vol. 71, No. 3, 1999, pp. 779-819. doi:10.1103/RevModPhys.71.779
NOTES
*Corresponding author.

