Journal of Modern Physics
Vol. 2 No. 7 (2011) , Article ID: 5836 , 6 pages DOI:10.4236/jmp.2011.27085
Quantum Statistical Properties of the Interactions of Atom-Field Entanglement between Conducting Plates
Mathematics Department, Faculty of Science, Taibah University, Madinah, Saudi Arabia
Mathematics Department, Faculty of Science, Al-Azhar University, Cairo, Egypt
E-mail: eiedkhalil@yahoo.com
Received March 18, 2011; revised May 12, 2011; accepted May 27, 2011
Keywords: TM₁ Mode, Von Neuman Entropy, Waveguide
ABSTRACT
The electromagnetic field inside perfectly conducting parallel plates interacting with two-level atom is investigated. The cavity modes are firstly quantized, allowing the effective Hamiltonian to be evaluated for an electric dipole located at an arbitrary point. Some statistical aspect of this effective Hamiltonian such as the temporal evolution of the atomic inversion and the von Neuman entropy are presented. Theses aspects are sensitive to the changes of the distance between the two plates, which control the number of the propagating of the cavity modes.
1. Introduction
The entanglement plays a central role in quantum information, quantum computation and communication, and quantum cryptography [1,2]. This is quite obvious from the efforts which have been devoted to characterize entanglement properties qualitatively and quantitatively and to apply them in quantum information. Also, it has been shown that the purification of the atomic state is actually independent of the nature of the initial pure state of the radiation field. Study of (atom/field) BoltzmannGibbs entropy as a system dynamical parameter and as a measure of field-atom correlation for the two-level Jaynes Cummings (JC) model [3] has been given in [4].
Maximally entangled states of two qubit systems have already been produced experimentally in photonic systems [5] and in the internal degrees of freedom of atoms interacting with a microwave cavity [6]. In the case of trapped ions [7], maximally entangled states have been created through the manipulation of their collective motion, but cavity QED devices are needed for transferring the stored information. Despite the diverse and recent theoretical proposals, see [8-10] and references therein, generation of maximally entangled states of two atoms inside an optical cavity has not yet been accomplished in the lab. The relevance of this achievement strongly relies on the possibility of using atoms in optical cavities as quantum networks [11], where quantum processing could take place among the entangled atoms and quantum information could be distributed among distant cavities [12-16].
In this paper we examine the entanglement between atom and electromagnetic field inside perfectly conducting parallel plates which acts as a totally confinement of all introduced fields into the vacuum region. Because of its relative simplicity as a confining structure, this system has a distinguished history as a testing ground for the confinement effects in quantum electrodynamics. However, as far as we know, the entanglement between atom and electromagnetic field inside perfectly conducting parallel plates in such a fundamental system have not previously been investigated. It is the primary purpose of this paper to examine the essential ingredients of the theory leading to the description of entanglement between atom and electromagnetic field inside perfectly conducting parallel plates. Such a study should provide the initial steps towards a more comprehensive understanding of the nature of entanglement process within confinement systems in general.
The material of this paper is organized as follows. In Section 2 we introduce the effective Hamiltonian for an atom coupled to the quantized field between the plates. By using the evolution operator, the expression of the dynamical operators and the wave function at any time t > 0 is obtained in Section 3. In Section 4 is devoted to a discussion of the atomic inversion and we find that it exhibits collapses and revivals for increases of the distance between the two plates decreases of the collapses regions. In Section 5 we write the mathematical form for the field entropy and we use numerical computations to examine the effect of the distance between the two plates on the evolution of the field entropy and hence entanglement between the atom and the field. Finally, we conclude the paper in Section 6 with some brief remarks.
2. Effective Hamiltonian
The atom of mass is characterized by its electric dipole moment of oscillation frequency interacting with the electromagnetic modes between two conducting plates. The effective Hamiltonian can be written as:
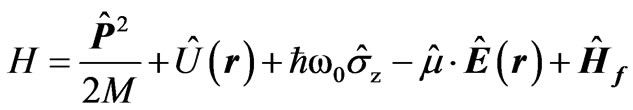 (1)
(1)
where P and r are the momentum and position vectors of the atomic centre of mass, which is assumed to be subject to a general potential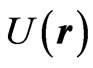 . In the two-level approximation the internal motion of the atom involves only two states:
. In the two-level approximation the internal motion of the atom involves only two states: 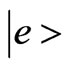 of energy
of energy 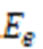 and
and  of energy
of energy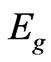 , such that
, such that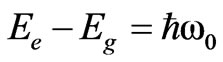 . For internal atomic states such that
. For internal atomic states such that 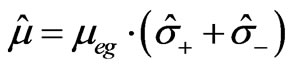 where the operators
where the operators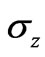 ,
, 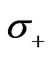 and
and 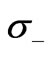 are the Pauli operators which satisfying the following commutation relations:
are the Pauli operators which satisfying the following commutation relations:
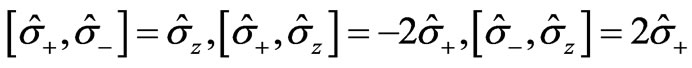 (2)
(2)
Finally  is the electric field operator and is the electromagnetic field Hamiltonian. The quantized fields between perfectly conducting plates are well known [17,18] and can be written in terms of transverse electric (s-polarized) and transverse magnetic (p-polarized) modes satisfying the electromagnetic boundary conditions at the plates. We write for
is the electric field operator and is the electromagnetic field Hamiltonian. The quantized fields between perfectly conducting plates are well known [17,18] and can be written in terms of transverse electric (s-polarized) and transverse magnetic (p-polarized) modes satisfying the electromagnetic boundary conditions at the plates. We write for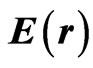 :
:
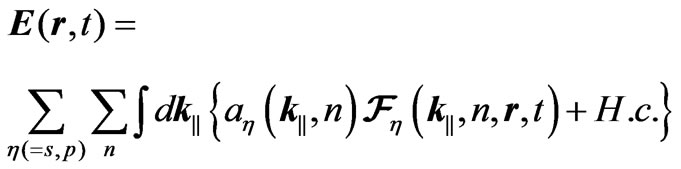 (3)
(3)
where  stands for “Hermitian conjugate” and
stands for “Hermitian conjugate” and 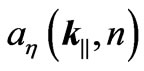 is the boson operator for the field mode of polarization
is the boson operator for the field mode of polarization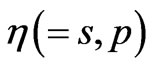 , characterized by the integer quantum number and the parallel weave vector
, characterized by the integer quantum number and the parallel weave vector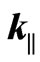 . The relevant commutation relation are:
. The relevant commutation relation are:
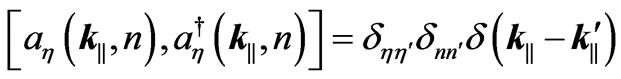 (4)
(4)
Finally, 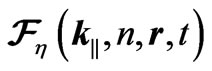 are the mode function satisfy electromagnetic boundary conditions at the conducting plates. Assuming that the parallel plates are positioned at
are the mode function satisfy electromagnetic boundary conditions at the conducting plates. Assuming that the parallel plates are positioned at  and
and , we have the mode functions:
, we have the mode functions:
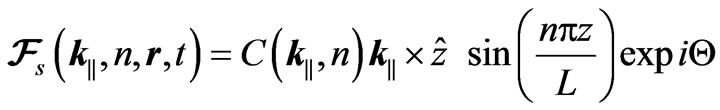 (5)
(5)
and
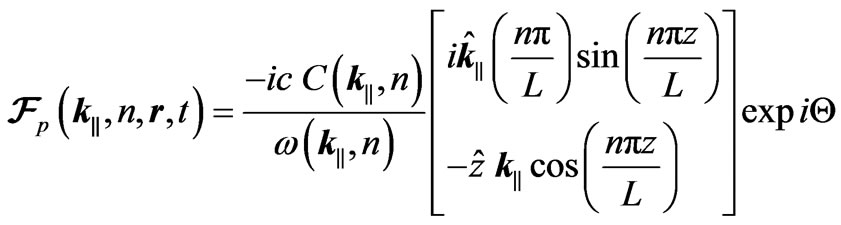 (6)
(6)
where carets denote unit vectors and we have written 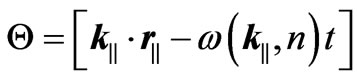 and
and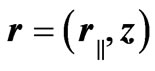 .
. 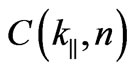 is the a normalization factor given by:
is the a normalization factor given by:
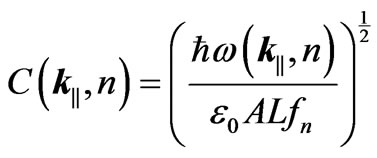 (7)
(7)
with 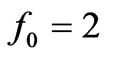 and
and  for
for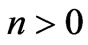 .
.  is the (large) surface area of the plates. Throughout
is the (large) surface area of the plates. Throughout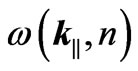 , is the mode frequency such that:
, is the mode frequency such that:
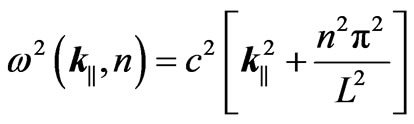 (8)
(8)
The  and
and 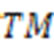 frequency branches for a typical parallel-plates system are shown in Figure 1. Depending on the value of the dipole frequency
frequency branches for a typical parallel-plates system are shown in Figure 1. Depending on the value of the dipole frequency 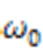 , contributions to the emission rate arise from all branches satisfying the condition
, contributions to the emission rate arise from all branches satisfying the condition
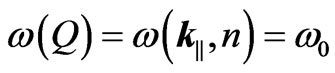 (9)
(9)
Since 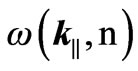 depends on the guide dimensions L entering via
depends on the guide dimensions L entering via , Equation (1) conceals the dependence on the chosen values of L. The plot of
, Equation (1) conceals the dependence on the chosen values of L. The plot of 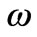 versus
versus 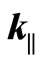 exhibits in Figure 1 a series of branches, one for each n, and it is easy to see that the minima of these branches (occurring at
exhibits in Figure 1 a series of branches, one for each n, and it is easy to see that the minima of these branches (occurring at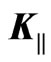 ) are separated by the frequency difference
) are separated by the frequency difference 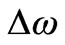 given by
given by
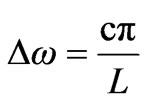 (10)
(10)
The branch separation therefore increases with decreasing L. The large value of 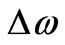 will be emphasized as a special feature here for cavities with typically sub-wavelength dimensions. On the other hand, the spontaneous decay of a dipole of frequency greater than
will be emphasized as a special feature here for cavities with typically sub-wavelength dimensions. On the other hand, the spontaneous decay of a dipole of frequency greater than 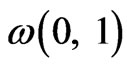 will involve the
will involve the 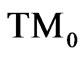 lowest branch as well as the
lowest branch as well as the 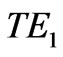 and
and 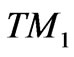 branches. If, in addition, this dipole is oriented along the axis, only the
branches. If, in addition, this dipole is oriented along the axis, only the 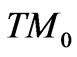 and
and 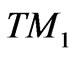 branches provides a decay channel, since the axial dipole cannot couple to the
branches provides a decay channel, since the axial dipole cannot couple to the  modes. These observations, which are significant for sub-micron system, are substantiated further with the calculation of the entanglement, as we now show.
modes. These observations, which are significant for sub-micron system, are substantiated further with the calculation of the entanglement, as we now show.
3. The Dynamical Operators
In this section we use the effective Hamiltonian for a two-level atom coupled to the quantized eletro-magnetic field between conducting plates in Equation (1) to study the dynamics of this system. For simplicity we write the effective Hamiltonian as follows (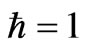 ):
):
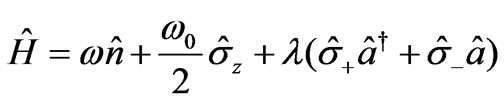 (11)
(11)
where we have taken the Raman-Nath approximation for the atomic Hamiltonian which leads to neglect the kinetic energy term. On the other hand the interaction Hamiltonian part was given in the standard interaction Hamiltonian for a two-level atom interacting with the electromagnetic field in the dipole approximation and the rotating-wave approximation. By introducing the following operators:
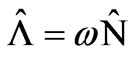 (12)
(12)
 (13)
(13)
with
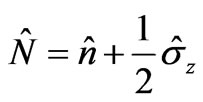 (14)
(14)
where 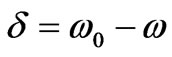 is the detuning parameter. It is easy to show that
is the detuning parameter. It is easy to show that 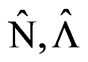 and
and  commute with each other and therefore they are constants of motion. The Hamiltonian (11) can be cast in the following form:
commute with each other and therefore they are constants of motion. The Hamiltonian (11) can be cast in the following form:
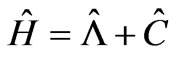 (15)
(15)
Now let us consider the atomic coherent state 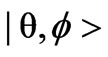 which acquires both excited state
which acquires both excited state 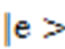 and ground state
and ground state 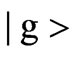 for the two-level atom in the following form:
for the two-level atom in the following form:
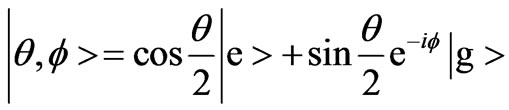 (16)
(16)
where 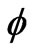 is the relative phase of the two atomic levels. To obtain the excited state we have to take
is the relative phase of the two atomic levels. To obtain the excited state we have to take 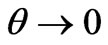 while to make the wave function describe the particle in the ground state we have to let
while to make the wave function describe the particle in the ground state we have to let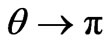 . Thus, if we consider the field to be initially in coherent state |
. Thus, if we consider the field to be initially in coherent state |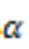 > then the initial state of the field takes the form:
> then the initial state of the field takes the form:
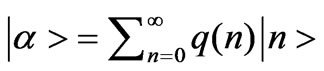 (17)
(17)
where 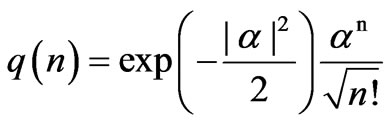
is the amplitude of states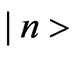 , and
, and 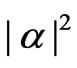 is the initial mean value of the operator
is the initial mean value of the operator  with
with  where
where  is the phase of coherent state. Assuming that at time
is the phase of coherent state. Assuming that at time 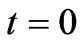 the system is in a pure state, thus the wave function is given by
the system is in a pure state, thus the wave function is given by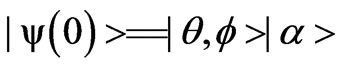 . Therefore, the wave function for the system at any time
. Therefore, the wave function for the system at any time 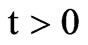 takes the form.
takes the form.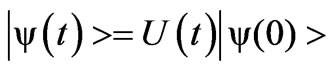 , where
, where 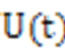 is the evolution operator. It is given by
is the evolution operator. It is given by
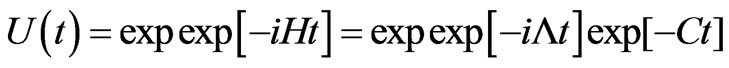 .
.
After straightforward calculations we find that:
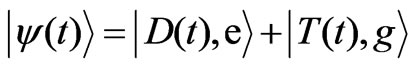 (18)
(18)
where
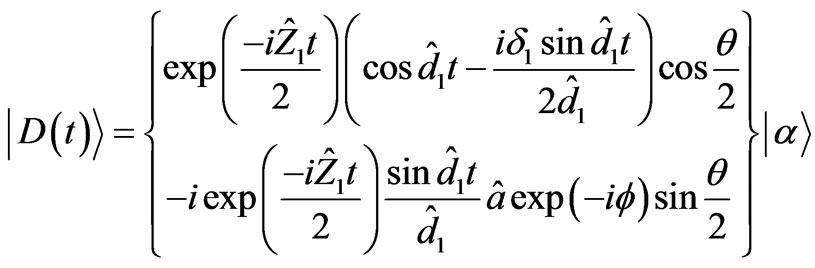
(19)
and
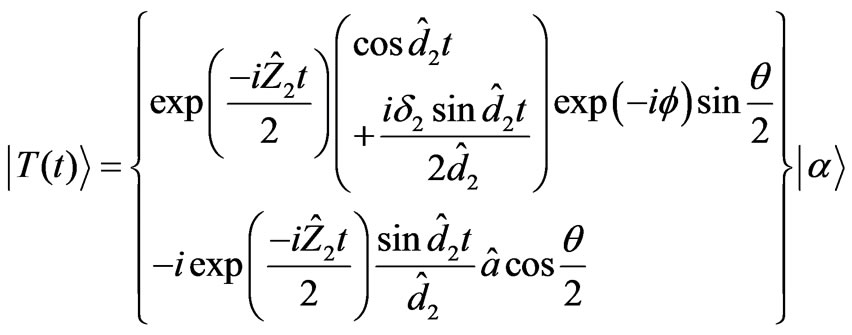
(20)
with
 (21)
(21)
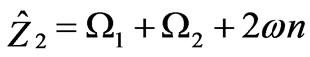 (22)
(22)
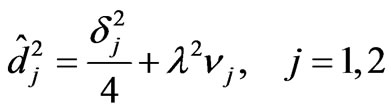 (23)
(23)
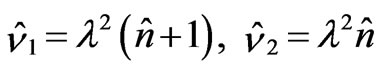 (24)
(24)
The reduced density matrix for the field is given by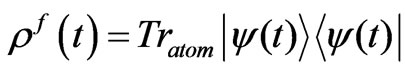 , such that :
, such that :
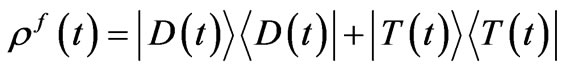 (25)
(25)
where 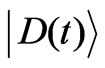 and
and 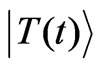 are given by Equations (19, 20) respectively.
are given by Equations (19, 20) respectively.
Once the wave function is computed, we can calculate any expectation value related to the atom or the field which is done in the next sections.
4. The Atomic Inversion
The level population inversion of the atom is one of the important atomic dynamic variables of the system. This in fact would give information about the behavior of the atom during the interaction period. The atomic inversion for the system which is given by
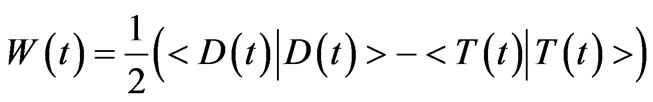 (26)
(26)
Therefore, we have plotted the function W(t) against the scaled time λt to display its behavior for the case in which Δ = 0 and for different values of the coupling parameter ratio z/L. Furthermore, we consider the mean photon number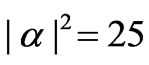 . In Figure 2(a) we take z/L = 0.15, as one can see that the function W(t) shows that the collapses and revivals of the standard JCM behaviour as would be expected. For z/L = 0.3, different behaviour is observed where the amplitude the oscillatory behaviour after the onset of interaction is decreased, while the collapse region as shows decaying. In the second period of the revival the function W(t) shows similar envelop to JCM, however, we observe a decrease in its amplitude. The mean of this envelop as a whole is related to the Rabi frequency which dependent to the coupling parameter (periodic function), see Figure 2(b). Increasing the value of the ratio z/L, namely z/L = 0.45 and 0.5 the same behaviour as well as elongation of the revival periods. The same behaviour can be reported, however, the phenomenon gets more pronounced as z/L increases, see Figures 2(c) and (d). As one can see this somewhat complicated behaviour may be thought of as a superposition of the standard JCM behaviour over a slowly varying envelop, as will be explained later. Thus we may conclude that, in the presence of the coupling interaction dependent on periodical function
. In Figure 2(a) we take z/L = 0.15, as one can see that the function W(t) shows that the collapses and revivals of the standard JCM behaviour as would be expected. For z/L = 0.3, different behaviour is observed where the amplitude the oscillatory behaviour after the onset of interaction is decreased, while the collapse region as shows decaying. In the second period of the revival the function W(t) shows similar envelop to JCM, however, we observe a decrease in its amplitude. The mean of this envelop as a whole is related to the Rabi frequency which dependent to the coupling parameter (periodic function), see Figure 2(b). Increasing the value of the ratio z/L, namely z/L = 0.45 and 0.5 the same behaviour as well as elongation of the revival periods. The same behaviour can be reported, however, the phenomenon gets more pronounced as z/L increases, see Figures 2(c) and (d). As one can see this somewhat complicated behaviour may be thought of as a superposition of the standard JCM behaviour over a slowly varying envelop, as will be explained later. Thus we may conclude that, in the presence of the coupling interaction dependent on periodical function  the atomic inversion shows oscillations in its behaviour, while the phenomenon of revivals and collapses occurs within these periods of the oscillations.
the atomic inversion shows oscillations in its behaviour, while the phenomenon of revivals and collapses occurs within these periods of the oscillations.
The general behavior of the function is changed markedly, however it shows the region of collapses decrease as the coupling ratio z/L increases. It is noted that the nonlinear interaction of the coupling interaction between
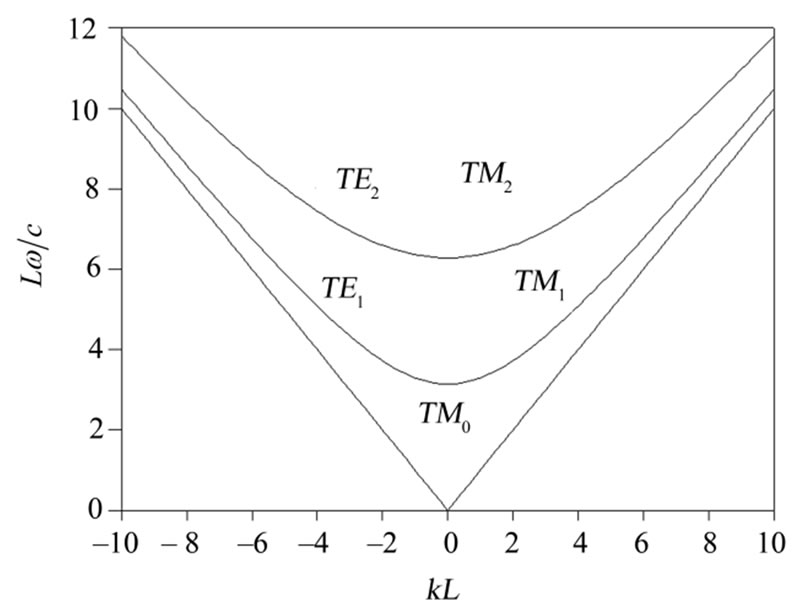
Figure 1. Dispersion curves showing the TM and TE branches of the guided modes in a planar mirror guide with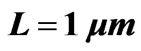 .
.
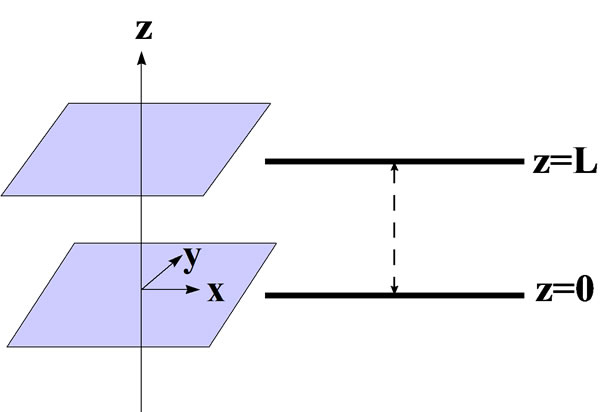
Figure 2. Schematic drawing of the planar mirror guide walls, separated by L. The z-coordinate is normal to the mirror surfaces, and the x and y coordinates are in the plane of one of the mirrors, as shown.
the atom and the field mode leads to the collapses and revivals to occur at short intervals which means that the energy is stored in the atomic system and it reach to the ground state as shown in Figure 1.
5. Quantum Field Entropy
We turn our attention to use the field entropy as a measure of the degree of entanglement between the fields and the atoms in order to discuss the entanglement of the present system. As one can see the quantum dynamics described by the Hamiltonian (13) leads to an entanglement between the fields and the atoms. Therefore, a suitable diagnostic tool to use in this case is the von Neuman entropy [4,19-22]
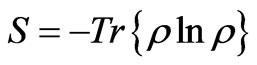 (27)
(27)
where ρ(t) is the density operator for a given quantum system and we set Boltzmann’s constant κ = 1. It is well known that for an initial pure state of the system then the entropy of the total system vanishes. Unitary evolution would not change this situation and S(t) is always zero under evolution. According to the Araki-Lieb theorem for a composite system then
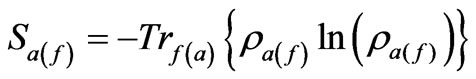 (28)
(28)
Thus when we start from an initial pure state under unitary evolution then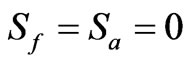 . However, if
. However, if 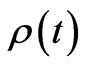 describes a mixed state, then
describes a mixed state, then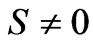 . Therefore, for the initial pure state where
. Therefore, for the initial pure state where 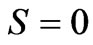 we can either use the field entropy
we can either use the field entropy 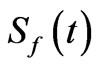 or the atomic entropy
or the atomic entropy 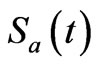 to measure the amount of entanglement between the two subsystems. From the previous studies it has been shown that, for the initially factored pure states of the atoms and cavity fields, the entropy of the atom and cavity field subsystems are identical so that
to measure the amount of entanglement between the two subsystems. From the previous studies it has been shown that, for the initially factored pure states of the atoms and cavity fields, the entropy of the atom and cavity field subsystems are identical so that . In this case the field entropy
. In this case the field entropy 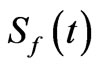 can be expressed in terms of the eigenvalues
can be expressed in terms of the eigenvalues 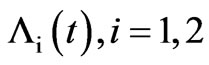 for the reduced field density operator
for the reduced field density operator 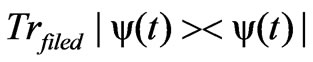 as,
as,
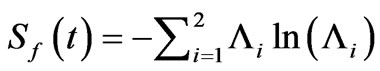 (29)
(29)
Now we turn our attention to examine numerically the dynamics of the field entropy where the same initial parameters of the atomic inversion will be used. In this case the entropy is dynamically reduced to the minimum values at the scaled time 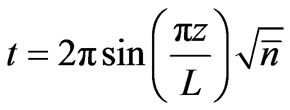 (where
(where 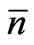
is the initial value of the photon number operator) and the minimum values of the function 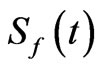 decayed gradually (Figure 3)
decayed gradually (Figure 3)
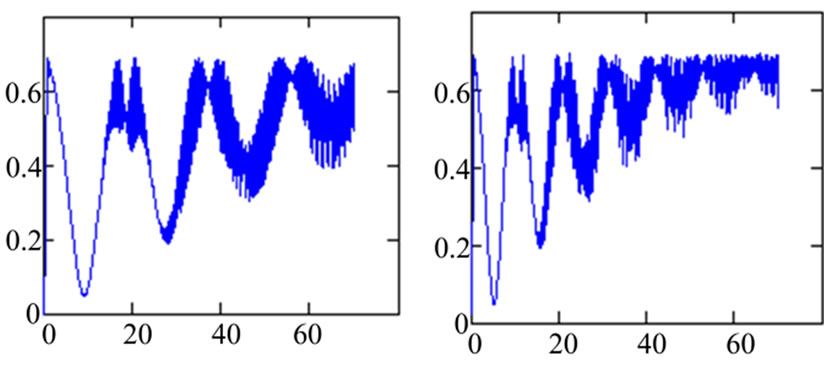
It is note that the entanglement increased to maximum values regularly before and after the quarter of the revivals time as observed in Figure 4(a). This behavior is completely in agreement with the entanglement of the Jaynes-Cumming model, which exhibits oscillatory behavior in a good correspondence with the revival patterns in the atomic inversion, and reduces to a pure state at the middle of the collapse time [16]. When we consider the case in which 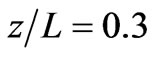 the function shows a similar behavior to that of the previous case but the fluctuations becomes more regular, see Figure 4(b). In this case the maximum entanglement occurred slightly faster compare with the previous case. Also we can report that the function decreases its minimum and consequently it approaches the pure state faster than that the case in which
the function shows a similar behavior to that of the previous case but the fluctuations becomes more regular, see Figure 4(b). In this case the maximum entanglement occurred slightly faster compare with the previous case. Also we can report that the function decreases its minimum and consequently it approaches the pure state faster than that the case in which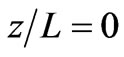 . More increasing in the value of the coupling parameter
. More increasing in the value of the coupling parameter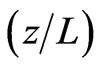 , leads to a more regular fluctuations in the function, see Figure 4(c). For example the function starts with rapid fluctuations until to reach its extreme (maximum and minimum values) and then backs to show oscillatory period. Here we may point out that the strong
, leads to a more regular fluctuations in the function, see Figure 4(c). For example the function starts with rapid fluctuations until to reach its extreme (maximum and minimum values) and then backs to show oscillatory period. Here we may point out that the strong
 (a)
(a)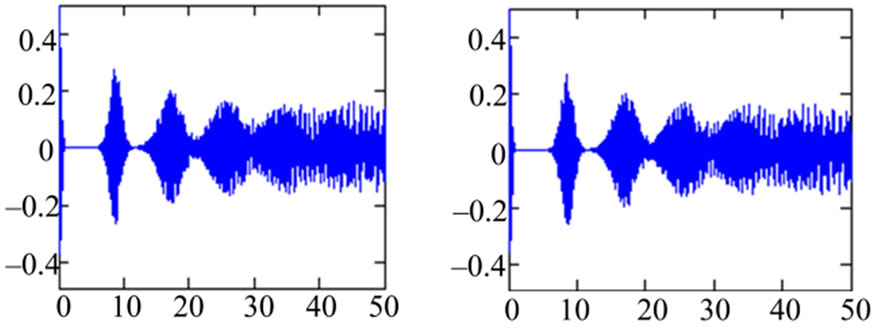 (b)
(b)
Figure 3. The atomic inversion against the scaled time λt for the atom initially in the excited state and the field in the coherent state α = 5 and for different values of the ratio z/L. a − z/L=0.15, b − z/L=0.3, c − z/L=0.45, d − z/L = 0.5.
 (a)
(a) (b)
(b)
Figure 4. The time evolution of the field entropy for the same initial condition and parameter of Figure 4.
oscillation in the atomic inversion decreases the degree of entanglement at particular regions between the time of half-revivals and increases the oscillatory behavior in the 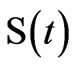 for the cases in which the parameter
for the cases in which the parameter 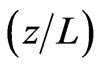 is small. The effects of the coupling interaction are more pronounced in some values for
is small. The effects of the coupling interaction are more pronounced in some values for 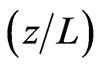 in the meantime the entanglement is greater than that the previous two cases see Figures 4(c) and (d). In general the disentanglement between the atom and the field increases when the atoms are in maximal states (collapses regions).
in the meantime the entanglement is greater than that the previous two cases see Figures 4(c) and (d). In general the disentanglement between the atom and the field increases when the atoms are in maximal states (collapses regions).
6. Conclusions
In this paper we have studied in detail the influence of the distance between the two plates (z/L) on the entanglement between atom and electromagnetic field inside perfectly conducting parallel plates. The cavity modes are first quantized, allowing the effective Hamiltonian to be evaluated for an electric dipole located at an arbitrary point. We have shown that in the limit of small separation of plates, especially when L = 500 nm, only the fundamental mode ( ) with zero cut-off frequency is allowed to propagate within the structure. Therefore the system became an exact mono-mode cavity operation and thus the atom only interact with a single cavity mode. This shows that the degree of entanglement is very sensitive to the parameter
) with zero cut-off frequency is allowed to propagate within the structure. Therefore the system became an exact mono-mode cavity operation and thus the atom only interact with a single cavity mode. This shows that the degree of entanglement is very sensitive to the parameter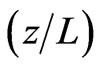 . For small values of the
. For small values of the 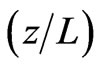 parameter, a decrease of the degree of the entanglement is shown, while for large values, an increase of the degree of entanglement is obtained. This is manifested in the degree of entanglement as it settles to a constant value for further increasing of the
parameter, a decrease of the degree of the entanglement is shown, while for large values, an increase of the degree of entanglement is obtained. This is manifested in the degree of entanglement as it settles to a constant value for further increasing of the 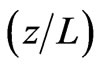 parameter. This means that one can control the degree of entanglement by using the
parameter. This means that one can control the degree of entanglement by using the 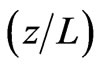 parameter.
parameter.
7. Acknowledgements
The author wish to express their gratitude to Prof. S. A. Al-Awfi for useful discussion and for prepare of these works.
REFERENCES
- M. Nielsen and I. Chuang, “Quantum Computation and Information,” Cambridge University Press, Cambridge, 2000.
- D. Bouwmeester, A. Ekert and A. Zeilinger, Eds., “The Physics of Quantum Information,” Springer, Berlin, 2000.
- E. T. Jaynes and F. W. Cummings, “Comparison of Quantum and Semiclassical Radiation Theory with Application to the Beam Maser,” Proceedings of IEEE, Vol. 51, No. 1, 1963, pp. 89-109. doi:10.1109/PROC.1963.1664
- S. J. D. Phoenix and P. L. Knight, “Establishment of an Entangled Atom-Field State in the Jaynes-Cummings Model,” Physical Review A, Vol. 44, No. 9, 1991, pp. 6023-6029. doi:10.1103/PhysRevA.44.6023
- P. G. Kwiat, K. Mattle, H. Weinfurter, A. Zeilinger, A. V. Sergienko and Y. Shih, “New High-Intensity Source of Polarization-Entangled Photon Pairs,” Physical Review Letters, Vol. 75, No. 24, 1995, pp. 4337-4342. doi:10.1103/PhysRevLett.75.4337
- E. Hagley, X. Maître, G. Nogues, C. Wunderlich, M. Brune, J. M. Raimond and S. Haroche, “Generation of Einstein-Podolsky-Rosen Pairs of Atoms,” Physical Review Letters, Vol. 79, No. 1, 1997, pp. 1-15. doi:10.1103/PhysRevLett.79.1
- Q. A. Turchette , C. S. Wood, B. E. King, C. J. Myatt, D. Leibfried, W. M. Itano, C. Monroe, and D. J. Wineland, “Deterministic Entanglement of Two Trapped Ions,” Physical Review Letters, Vol. 81, No. 17, 1998, pp. 3631-3638. doi:10.1103/PhysRevLett.81.3631
- A. Beige, D. Braun, B. Tregenna and P. L. Knight, “Quantum Computing Using Dissipation to Remain in a Decoherence-Free Subspace,” Physical Review Letters, Vol. 85, No. 8, 2000, pp. 1762-1767. doi:10.1103/PhysRevLett.85.1762
- S. Sorensen and K. Molmer, “Probabilistic Generation of Entanglement in Optical Cavities,” Physical Review Letters, Vol. 90, No. 12, 2003, pp. 903-908. doi:10.1103/PhysRevLett.90.127903
- C. Marr, A. Beige and G. Rempe, “Entangled-State Preparation via Dissipation-Assisted Adiabatic Passages,” Physical Review A, Vol. 68, No. 3, 2003, pp. 033817- 033822. doi:10.1103/PhysRevA.68.033817
- J. I. Cirac, P. Zoller, H. J. Kimble and H. Mabuchi, “Quantum State Transfer and Entanglement Distribution among Distant Nodes in a Quantum Network,” Physical Review Letters, Vol. 78, No. 16, 1997, pp. 3221-3226. doi:10.1103/PhysRevLett.78.3221
- K. Molmer, “Entanglement of Distant Atoms by a Continuous Supply of Quantum Correlated Photons,” Optics Communications, Vol. 179, No. 1-6, 2000, pp. 429-435.
- X.-L. Feng, X.-D. Li, S.-Q. Gong and Z.-Z. Xu, “Entangling Distant Atoms by Interference of Polarized Photons,” Physical Review Letters, Vol. 90, No. 21, 2003, pp. 217902-217907. doi:10.1103/PhysRevLett.90.217902
- E. Browne, M. B. Plenio and S. F. Huelga, “Robust Creation of Entanglement between Ions in Spatially Separate Cavities,” Physical Review Letters, Vol. 91, No. 6, 2003, pp. 067901-067906. doi:10.1103/PhysRevLett.91.067901
- B. Kraus and J. I. Cirac, “Discrete Entanglement Distribution with Squeezed Light,” Physical Review Letters, Vol. 92, No. 1, 2004, pp. 602-608. doi:10.1103/PhysRevLett.92.013602
- S. A. Al-Awfi and E. M. Khalil, “Atom-Field Entanglement between Conducting Plates,” International Review of Physics, Vol. 3, 2008, pp. 147-153.
- S. Al-Awfi and M. Babiker, “Atom Dynamics between Conducting Plates,” Physical Review A, Vol. 58, No. 3, 1998, pp. 2274-2281. doi:10.1103/PhysRevA.58.2274
- S. Bougouffa and S. Al-Awfi, “The Dynamics of the Jaynes-Cummings Model in Nanostructures,” Physica Scripta, Vol. 2009, No. T135, 2009, p. 014011. doi:10.1088/0031-8949/2009/T135/014011
- A.-S. F. Obada, M. M. A. Ahmed, F. K. Faramawy and E. M. Khalil, “Entropy and Entanglement of the Nonlinear Jaynes-Cummings Model,” Chinese Journal of Physics, Vol. 42, No. 1, 2004, pp. 79-86.
- M. M. A. Ahmed, E. M. Khalil and A.-S. F. Obada, “Generation of a Nonlinear Stark Shift through the Adiabatic Elimination Method,” Optics Communications, Vol. 254, No. 1-3, 2005, pp. 76-84. doi:10.1016/j.optcom.2005.05.016
- A.-S. F. Obada, M. M. A. Ahmed and E. M. Khalil, “Generation of a Nonlinear Two-Mode Stark Shift through the Adiabatic Elimination Method,” Journal of Modern Optics, Vol. 53, No. 8, 2006, pp. 1149-1155. doi:10.1080/09500340600551440
- A.-S. F. Obada, M. M. A. Ahmed, F. K. Faramawy and E. M. Khalil, “Influence of Kerr-Like Medium on a Nonlinear Two-Level Atom,” Chaos, Solitons & Fractals, Vol. 28, No. 4, 2006, pp. 983-988. doi:10.1016/j.chaos.2005.08.176

