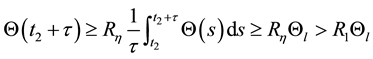Applied Mathematics
Vol.06 No.11(2015), Article ID:60782,8 pages
10.4236/am.2015.611171
The Analysis of an SIRS Epidemic Model with Discrete Delay on Scale-Free Network
Tao Li1, Qiming Liu1, Baochen Li2
1Institute of Applied Mathematics, Shijiazhuang Mechanical Engineering College, Shijiazhuang, China
2Department of Science and Research, Shijiazhuang Mechanical Engineering College, Shijiazhuang, China
Email: leo_119@163.com, lqmmath@163.com, testability83@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 September 2015; accepted 26 October 2015; published 29 October 2015
ABSTRACT
A new epidemic SIRS model with discrete delay on scale-free network is presented. We give the formula of the basic reproductive number for the model and prove that the disease dies out when the basic reproductive number is less than unity, while the disease is uniformly persistent when the basic reproductive number is more than unity. Numerical simulations are given to demonstrate the main results.
Keywords:
Scale-Free Network, Epidemic Spreading, Attractivity, Uniformly Persistence, Time Delay

1. Introduction
Since the modelling of the seminal works on the scale-free network, in which the probability of
 for any node with
for any node with
 links to other nodes is distributed according to the power law
links to other nodes is distributed according to the power law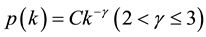 , suggested
, suggested
by Barabá and Albert [1] , it is well known that the real disease transmission networks exhibit scale-free properties (see for example [2] [3] ), and the spreading of epidemic disease on scale-free network has been studied by many researchers [4] - [21] .
Continuous time deterministic epidemic models are traditionally formulated as systems of ordinary differential equations. More realistic models should include some peat states of these systems, and ideally, a real system should be modeled by delay differential equation. Time delay plays an important role in propagation process of the epidemic, we can simulate the latent period of infectious diseases, the infections period of patients and the immunity period of recovery of the disease with time delay. Much attention has been given to the dynamical behaviors of the epidemic spreading model with time delay on homogeneous network [18] . However, up to now, compared with studies of the dynamical behaviors of the epidemic models with time delays on hetergeneous network, only a few attentions have been paid to them on heterogeneous networks. Recently, Liu and Xu presented a delay differential equation SEIRS epidemic model with discrete time delays which represent the latent period and the immune period [19] . Liu and Deng et al. discussed epidemic SIS model with discrete time delay which represents the infectious period [20] , they obtained the basic reproduction number and discussed the persistence of the disease. Wang and Wang et al. discussed an epidemic SIR model with discrete time delay which represented the latent period [21] . Motivated by these, in this paper, we will present a suitable epidemic SIRS model with discrete delay which represents the infectious period on scale-free network using functional differential equations to investigate the epidemic spreading.
The rest of this paper is organized as follows: The SIRS model on scale-free network with discrete delay is presented in Section 2. The basic reproductive number is given and dynamical behaviour of the system is analyzed in Section 3. Numerical simulations are given to demonstrate the main results in Section 4. Conclusion is finally drawn in Section 5.
2. The SIRS Model with Discrete Delay
Suppose that the size of the network is a constant N during the period of epidemic spreading, we also suppose that the degree of each degree is time invariant. Let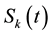 ,
,
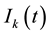 and
and
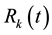 be the relative density of susceptible nodes, infected nodes and recovered nodes of connectivity k at time t, respectively. Obviously, the following normalization condition holds due to the fact that the number of total nodes with degree k is a constant
be the relative density of susceptible nodes, infected nodes and recovered nodes of connectivity k at time t, respectively. Obviously, the following normalization condition holds due to the fact that the number of total nodes with degree k is a constant
 during the period of epidemic spreading.
during the period of epidemic spreading.
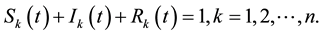
The dynamical equation for the density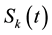 ,
,
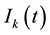 and
and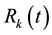 , at the mean-field level, satisfy the following system when
, at the mean-field level, satisfy the following system when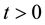 :
:
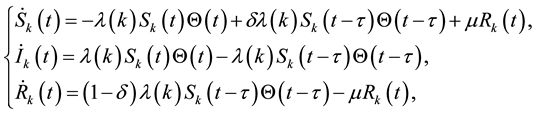 (1)
(1)
where
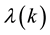 is the correlated (k-dependent) infection rate such as
is the correlated (k-dependent) infection rate such as
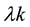 [5] [8] [20] ,
[5] [8] [20] ,
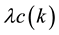 [6] and so on, and
[6] and so on, and


may become susceptible nodes because they are recovered and are not immunized, where
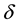




where








The initial condition of system (1) is
where
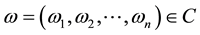


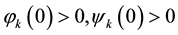


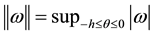


3. Dynamical Behaviors of the Model
Denote

where


Obviously, the second equation of system (1) can be furthermore transformed into the following integral equation:

Note that




Theorem 1. The system (5) has always a disease-free equilibrium


Proof. Denote
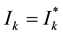


where

It yields that

Substituting it into (7), we obtain the self-consistency equality

Obviously,


and
Hence, if


Theorem 2. Consider the system (5), the following assertions hold.
(1) If

(2) If


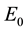
Proof. First, According to the Equation (4), similar to the proof of Theorem 1 in [20] , we can obtain that the equilibrium

Second, motivated by the work in [22] , we will prove that conclusion (2) in Theorem 2 holds step by step, i.e., we prove that the disease is uniformly persistent when
Step 1. We will prove that for any


Since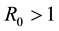

in which
Suppose


for

for


for


It follows from (2) and (12) that

Set




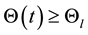

which leads to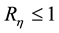
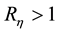
Choose a positive constant


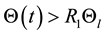

If the claim is not valid, there exists a

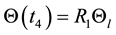


Thus
which leads to

for

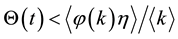
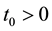


Step 2. We will prove that there exists a positive constant


Since it is impossible that




Case 1:

Case 2:


Suppose











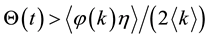

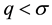


Let us define




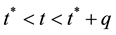



Hence,



At last, since




The basic reproductive number for system (4) is




Remark. When

4. Numerical Simulations
The basic reproductive number for system (1) is

Note that an epidemic always occurs on a finite networks in the real world, the maximum connectivity n of any node is related to the network age, which is measured as the number of nodes N [8] [9] :

where m is the minimum connectivity of the network. It follows from (14) and (15) that

Now we present the results of numerical simulations by using MATLAB 7.0 to support the results obtained in previous sections. Since the equilibria were obtained from system (5), the simulations are based on system (5)
and a scale-free network in which the degree distribution is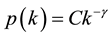











Figure 1. The time series of system (5) with


Figure 2. The time series of system (5) with


Figure 3. The time series of system (5) with

From the dynamical behaviors of the SIRS model (5) shown in Figure l and Figure 2, it can be seen that if

According to







5. Conclusion
An SIRS model with discrete delay has been proposed for investigating the dynamical behaviors of the epidemics on scale-free networks. Through mathematical analysis, we obtained the basic reproduction number





Cite this paper
TaoLi,QimingLiu,BaochenLi, (2015) The Analysis of an SIRS Epidemic Model with Discrete Delay on Scale-Free Network. Applied Mathematics,06,1939-1946. doi: 10.4236/am.2015.611171
References
- 1. Barabási, A.L. and Alber, R. (1999) Emergence of Scaling in Random Networks. Science, 286, 509-512.
http://dx.doi.org/10.1126/science.286.5439.509 - 2. Small, M. and Tse, C.K. (2005) Small World and Scale Free Model of Transmission of SARS. International Journal of Bifurcation and Chaos, 15, 1745-1755.
http://dx.doi.org/10.1142/S0218127405012776 - 3. Small, M., Walker, D.M. and Tse, C.K. (2007) Scale Free Distribution of Avian Influenza Outbreaks. Physical Review Letters, 99, Article ID: 188702.
http://dx.doi.org/10.1103/PhysRevLett.99.188702 - 4. Pastor-Satorras, R. and Vespignani, A. (2001) Epidemic Spreading in Scale Free Networks. Physical Review Letters, 86, 3200-3203.
http://dx.doi.org/10.1103/PhysRevLett.86.3200 - 5. Pastor-Satorras, R. and Vespignani, A. (2002) Epidemic Dynamics in Finite Size Scale-Free Networks. Physical Review E, 65, Article ID: 035108.
http://dx.doi.org/10.1103/PhysRevE.65.035108 - 6. Olinky, R. and Stone, L. (2004) Unexpected Epidemic Thresholds in Heterogeneous Networks: The Role of Disease Transmission. Physical Review E, 70, Article ID: 030902.
http://dx.doi.org/10.1103/PhysRevE.70.030902 - 7. Yang, R., Ren, J., et al. (2007) Epidemic Spreading on Hererogeneous Networks with Identical Infectivity. Physics Letters A, 364, 189-193.
http://dx.doi.org/10.1016/j.physleta.2006.12.021 - 8. Cheng, X., Liu, X., Chen, Z. and Yuan, Z. (2009) Spreading Behavior of SIS Model with Non-Uniform Transmission on Scale-Free Networks. The Journal of Universities of Posts and Telecommunications, 16, 27-31.
http://dx.doi.org/10.1016/S1005-8885(08)60173-9 - 9. Zhang, H. and Fu, X. (2009) Spreading of Epidemics on Scale-Free Networks with Nonlinear Infectivity. Nonlinear Analysis, 70, 3273-3278.
http://dx.doi.org/10.1016/j.na.2008.04.031 - 10. Li, K., Small, M., Zhang, H. and Fu, X. (2010) Epidemic Outbreaks on Networks with Effective Contacts. Nonlinear Analysis: RWA, 11, 1017-1025.
http://dx.doi.org/10.1016/j.nonrwa.2009.01.046 - 11. Fu, X.C., Small, M., Walker, D.M. and Zhang, H.F. (2008) Epidemic Dynamics on Scale-Free Networks with Piecewise Linear Infectivity and Immunization. Physical Review E, 77, Article ID: 036113.
http://dx.doi.org/10.1103/PhysRevE.77.036113 - 12. Zhang, J.P. and Jin, Z. (2011) The Analysis of an Epidemic Model on Networks. Applied Mathematics and Computation, 217, 7053-7064.
http://dx.doi.org/10.1016/j.amc.2010.09.063 - 13. Zhu, G.H., Fu, X.C. and Chen, G.R. (2013) Global Attractivity of a Network-Based Epidemics SIS Model with Nonlinearn Infectivity. Communications in Nonlinear Science and Numerical Simulation, 17, 2588-2594.
- 14. Gong, Y.W., Song, Y.R. and Jiang, G.P. (2012) Epidemic Spreading in Scale-Free Networks Including the Effect of Individual Vigilance. Chinese Physics B, 21, Article ID: 010205.
http://dx.doi.org/10.1088/1674-1056/21/1/010205 - 15. Li, T., Wang, Y.M. and Guan, Z.H. (2014) Spreading Dynamics of a SIQRS Epidemic Model on Scale-Free Networks. Communications in Nonlinear Science and Numerical Simulation, 19, 686-692.
http://dx.doi.org/10.1016/j.cnsns.2013.07.010 - 16. Liu, J.L. and Zhang, T.L. (2011) Epidemic Spreading of an SEIRS Model in Scale-Free Networks. Communications in Nonlinear Science and Numerical Simulation, 16, 3375-3384.
http://dx.doi.org/10.1016/j.cnsns.2010.11.019 - 17. Chen, L.J. and Sun, J.T. (2014) Global Stability and Optimal Control of an SIRS Epidemic Model on Heterogeneous Networks. Physica A: Statistical Mechanics and Its Applications, 410, 196-204.
http://dx.doi.org/10.1016/j.physa.2014.05.034 - 18. Ma, Z.E. and Li, J. (2009) Dynamical Modelling and Analysis of Epidemics. World Scientific Publishing Company, Singapore.
- 19. Liu, X. and Xu, D.J. (2012) Analysis of Epidemic Disease Models with Vertical Transmission in Complex Networks. Acta Mathematicae Applicatae Sinica, English Series, 28, 63-74.
http://dx.doi.org/10.1007/s10255-012-0094-1 - 20. Liu, Q.M., Deng, C.S. and Sun, M.C. (2014) The Analysis of an Epidemic Model with Time Delay on Scale-Free Networks. Physica A: Statistical Mechanics and Its Applications, 410, 79-87.
http://dx.doi.org/10.1016/j.physa.2014.05.010 - 21. Wang, J.R., Wang, J.P., Liu, M.X. and Liu, Y.W. (2014) The Analysis of an Epidemic Model with Time Delay on Scale-Free Networks. Physica A: Statistical Mechanics and Its Applications, 410, 268-275.
http://dx.doi.org/10.1016/j.physa.2014.05.011 - 22. Wang, W.D. and Ma, Z.E. (2002) Global Dynamics of an Epidemic Model with Time Delay. Nonlinear Analysis: Real World Applications, 3, 365-373.
http://dx.doi.org/10.1016/S1468-1218(01)00035-9