Applied Mathematics
Vol.06 No.12(2015), Article ID:61487,8 pages
10.4236/am.2015.612184
On the Approximate Solution of Fractional Logistic Differential Equation Using Operational Matrices of Bernstein Polynomials
R. F. Al-Bar
Department of Mathematics, Faculty of Science, Umm Al-Qura University, Makkah, Saudi Arabia

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 31 August 2015; accepted 23 November 2015; published 26 November 2015

ABSTRACT
In this paper, operational matrices of Bernstein polynomials (BPs) are presented for solving the non-linear fractional Logistic differential equation (FLDE). The fractional derivative is described in the Riemann-Liouville sense. The operational matrices for the fractional integration in the Riemann-Liouville sense and the product are used to reduce FLDE to the solution of non-linear system of algebraic equations using Newton iteration method. Numerical results are introduced to satisfy the accuracy and the applicability of the proposed method.
Keywords:
Fractional Logistic Equation, Riemann-Liouville Fractional Derivatives, Riemann-Liouville Fractional Integral, Operational Matrix, Bernstein Polynomials

1. Introduction
It is well-known that the fractional differential equations (FDEs) have been the focus of many studies due to their frequent appearance in various applications, such as in fluid mechanics, viscoelasticity, biology, physics and engineering applications, for more details see for example ([1] [2] ). Consequently, considerable attention has been given to the efficient numerical solutions of FDEs of physical interest, because it is difficult to find exact solutions. Different numerical methods have been proposed in the literature for solving FDEs ( [3] - [6] ). Recently, several numerical and approximate methods to solve FDEs have been given, such as variational iteration method [7] , homotopy perturbation method [7] and collocation method ([8] -[13] ).
The fractional Logistic model can obtain by applying the fractional derivative operator on the Logistic equation. The model is initially published by Pierre Verhulst in 1838 ( [14] [15] ). The continuous Logistic model is described by first order ordinary differential equation. The discrete Logistic model is simple iterative equation that reveals the chaotic property in certain regions [16] . There are many variations of the population modeling [17] . The Verhulst model is the classic example to illustrate the periodic doubling and chaotic behavior in dynamical system [16] . The model is described the population growth may be limited by certain factors like population density ( [15] [17] ).
The solution of Logistic equation explains the constant population growth rate which does not include the limitation on food supply or spread of diseases [15] . The solution curve of the model increases exponentially from
the multiplication factor up to saturation limit which is maximum carrying capacity [15] , 
where N is the population with respect to time, 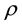 is the rate of maximum population growth and K is the carrying capacity. The solution of continuous Logistic equation is in the form of constant growth rate as in formula
is the rate of maximum population growth and K is the carrying capacity. The solution of continuous Logistic equation is in the form of constant growth rate as in formula 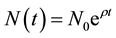 where
where 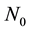 is the initial population [18] .
is the initial population [18] .
In this article, we consider FLDE of the form
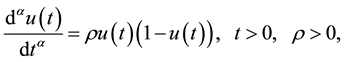 (1)
(1)
the parameter 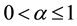 refers to the fractional order derivative
refers to the fractional order derivative
We also assume an initial condition
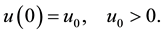 (2)
(2)
The exact solution to this problem at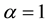 , is
, is 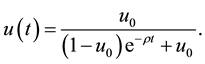
The existence and the uniqueness of the proposed problem (1) are introduced in details in ( [19] [20] ).
Khader and Hendy [21] introduced a new approximate formula of the fractional derivative using Legendre series expansion and used it to solve numerically the fractional delay equation. In this article, we extended this work to study the numerical solution of the non-linear FLDE. An approximate formula of the fractional derivative is presented. Special attention is given to study the convergence analysis and estimate an upper bound of the error of the introduced formula.
2. Preliminaries and Notations
In this section, we present some necessary definitions and mathematical preliminaries of the fractional calculus theory and the Bernstein polynomials that will be required in the present paper.
The Fractional Integral and Derivative Operators
We present some necessary definitions and mathematical preliminaries of the fractional calculus theory that will be required in the present paper.
Definition 1.
The Riemann-Liouville fractional integral operator 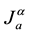 of order
of order 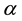 is defined on
is defined on 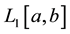 in the following form
in the following form
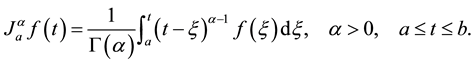 (3)
(3)
Definition 2.
The Riemann-Liouville fractional derivative operator 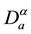 of order
of order 


Definition 3.
The Caputo fractional derivative operator 



Similar to integer-order differentiation, Caputo fractional derivative operator is a linear operation
where 



We use the ceiling function 



For more details on fractional derivatives definitions and its properties see ( [1] [2] ).
Lemma 1.
If 




3. Bernstein Polynomials and Their Properties
Definition 4.
The 


where 
The Bernstein polynomials have the following properties
1) 


2) 


3) 

4)
5) They satisfy symmetry
6)
7)

Since the set 




We can write

Bernstein polynomials [23] .
4. BPs Operational Matrix of Riemann-Liouville Fractional Integration
Theorem 1. [23]
The Bernstein polynomials operational matrix 


Definition 5.
We can define the dual matrix 

where

Lemma 2. [24]
Let 


we can find the unique vector 

from space


Definition 6.
Let 

It can be shown that is uniformly convergent on the interval
Theorem 2.
Given a function 


The Bernstein polynomials operational matrix are used for solving many class of fractional differential equations, they used to solve numerically the fractional heat-and wave-like equations [25] and the multi-term orders fractional differential equations [26] and others [27] .
5. Implementation of Bernstein Polynomials Operational Matrix for Solving FLDE
In this section, we introduce a numerical algorithm using Bernstein polynomials operational matrix method for solving the fractional Logistic differential equation of the form (1).
The proposed technique will apply as in the following steps:
1) We use the initial condition (2) to reduce the given problem (1) to a problem with zero initial condition. So, we define

where 

2) Substituting (17) in (1) and (2), we have an initial-value problem as follows

where 


3) Using (10) in Lemma 1 we can write

4) Using Lemma 3.3 in [23] , the inputs 


where P and Q are known 

5) From (9), (13), (19), (20) and (21), we have

where
6) By substituting (21) and (22) into (18), we obtain

7) Then, from Lemma 3.5 in [23] we have



Therefore we can reduce (23) by (24)-(26) as

We obtain the following non-linear system of algebraic equations

8) By solving this system we can obtain the vector C. Then, we can get

The numerical results of the proposed problem (1) are given in Figure 1 and Figure 2 with different values of 








From these figures we can conclude that the obtained numerical solutions are in excellent agreement with the exact solution.
6. Conclusion and Remarks
In this article, we used operational matrices of the Riemann-Liouville fractional integral and the product by Bernstein polynomials for solving the fractional Logistic differential equation. The properties of these operational
Figure 1. A comparison between the approximate solution and the exact solution at 

Figure 2. The behavior of the approximate solution using the proposed method at 

matrices are used to reduce FLDE to a non-linear system of algebraic equations which solved by Newton iteration method. From the obtained numerical results, we can conclude that this method gives results with an excellent agreement with the exact solution. All numerical results are obtained using Matlab program 8.
Acknowledgements
We thank the Editor and the referee for their comments.
Cite this paper
R. F.Al-Bar, (2015) On the Approximate Solution of Fractional Logistic Differential Equation Using Operational Matrices of Bernstein Polynomials. Applied Mathematics,06,2096-2103. doi: 10.4236/am.2015.612184
References
- 1. Oldham, K.B. and Spanier, J. (1974) The Fractional Calculus. Academic Press, New York.
- 2. Podlubny, I. (1999) Fractional Differential Equations. Academic Press, New York.
- 3. Burden, R.L. and Faires, J.D. (1993) Numerical Analysis. PWS, Boston.
- 4. Sweilam, N.H., Khader, M.M. and Nagy, A.M. (2011) Numerical Solution of Two-Sided Space-Fractional Wave Equation Using Finite Difference Method. Journal of Computional and Applied Mathematics, 235, 2832-2841.
http://dx.doi.org/10.1016/j.cam.2010.12.002 - 5. Sweilam, N.H., Khader, M.M. and Mahdy, A.M.S. (2012) Numerical Studies for Solving Fractional-Order Logistic Equation. International Journal of Pure and Applied Mathematics, 78, 1199-1210.
- 6. Sweilam, N.H., Khader, M.M. and Mahdy, A.M.S. (2012) Numerical Studies for Fractional-Order Logistic Differential Equation with Two Different Delays. Journal of Applied Mathematics, 2012, 1-14.
http://dx.doi.org/10.1155/2012/764894 - 7. Sweilam, N.H., Khader, M.M. and Al-Bar, R.F. (2007) Numerical Studies for a Multi-Order Fractional Differential Equation. Physics Letters A, 371, 26-33.
http://dx.doi.org/10.1016/j.physleta.2007.06.016 - 8. Khader, M.M. (2011) On the Numerical Solutions for the Fractional Diffusion Equation. Communications in Nonlinear Science and Numerical Simulation, 16, 2535-2542.
http://dx.doi.org/10.1016/j.cnsns.2010.09.007 - 9. Khader, M.M. (2013) Numerical Treatment for Solving the Perturbed Fractional PDEs Using Hybrid Techniques. Journal of Computational Physics, 250, 565-573.
http://dx.doi.org/10.1016/j.jcp.2013.05.032 - 10. Khader, M.M. and Hendy, A.S. (2013) A Numerical Technique for Solving Fractional Variational Problems. Mathematical Methods in Applied Sciences, 36, 1281-1289.
http://dx.doi.org/10.1002/mma.2681 - 11. Khader, M.M. and Babatin, M.M. (2013) On Approximate Solutions for Fractional Logistic Differential Equation. Mathematical Problems in Engineering, 2013, Article ID: 391901.
http://dx.doi.org/10.1155/2013/391901 - 12. Khader, M.M., EL Danaf, T.S. and Hendy, A.S. (2013) A Computational Matrix Method for Solving Systems of High Order Fractional Differential Equations. Applied Mathematical Modelling, 37, 4035-4050.
http://dx.doi.org/10.1016/j.apm.2012.08.009 - 13. Khader, M.M., Sweilam, N.H. and Mahdy, A.M.S. (2013) Numerical Study for the Fractional Differential Equations Generated by Optimization Problem Using Chebyshev Collocation Method and FDM. Applied Mathematics and Information Science, 7, 2011-2018.
http://dx.doi.org/10.12785/amis/070541 - 14. Cushing, J.M. (1998) An Introduction to Structured Population Dynamics. Society for Industrial and Applied Mathematics, Philadelphia.
http://dx.doi.org/10.1137/1.9781611970005 - 15. Pastijn, H. (2006) Chaotic Growth with the Logistic Model of P.-F. Verhulst. In: Ausloos, M. and Dirickx, M., Eds., The Logistic Map and the Route to Chaos, Understanding Complex Systems, Springer, Berlin, 3-11.
http://dx.doi.org/10.1007/3-540-32023-7_1 - 16. Alligood, K.T., Sauer, T.D. and Yorke, J.A. (1996) Chaos: An Introduction to Dynamical Systems. Springer, New York.
- 17. Ausloos, M. (2006) The Logistic Map and the Route to Chaos: From the Beginnings to Modern Applications XVI. 411 p.
- 18. Suansook, Y. and Paithoonwattanakij, K. (2009) Dynamic of Logistic Model at Fractional Order. IEEE International Symposium on Industrial Electronics, Seoul, 5-8 July 2009, 718-723.
http://dx.doi.org/10.1109/isie.2009.5219765 - 19. El-Sayed, A.M.A., El-Mesiry, A.E.M. and El-Saka, H.A.A. (2007) On the Fractional-Order Logistic Equation. Applied Mathematics Letters, 20, 817-823.
http://dx.doi.org/10.1016/j.aml.2006.08.013 - 20. El-Sayed, A.M.A., Gaafar, F.M. and Hashem, H.H. (2004) On the Maximal and Minimal Solutions of Arbitrary Orders Nonlinear Functional Integral and Differential Equations. Mathematical Sciences Research Journal, 8, 336-348.
- 21. Khader, M.M. and Hendy, A.S. (2012) The Approximate and Exact Solutions of the Fractional-Order Delay Differential Equations Using Legendre Pseudospectral Method. International Journal of Pure and Applied Mathematics, 74, 287-297.
- 22. Cheney, E.W. (1982) Introduction to Approximation Theory. 2nd Edition, AMS Chelsea Publishing, Providence.
- 23. Alipour, M., Rostamy, D. and Baleanu, D. (2013) Solving Multidimensional FOCPs with Inequality Constraint by BPs Operational Matrices. Journal of Vibration and Control, 19, 2523-2540.
http://dx.doi.org/10.1177/1077546312458308 - 24. Kreyszig, E. (1978) Introduction Functional Analysis with Applications. John Wiley & Sons, New York.
- 25. Rostamy, D. and Karimi, K. (2012) Bernstein Polynomials for Solving Fractional Heat- and Wave-Like Equations. Fractional Calculus and Applied Analysis, 15, 556-571.
http://dx.doi.org/10.2478/s13540-012-0039-7 - 26. Rostamy, D., Alipour, M., Jafari, H. and Baleanu, D. (2013) Solving Multi-Term Orders Fractional Differential Equations by Operational Matrices of BPs with Convergence Analysis. Romanian Reports in Physics, 65, 334-349.
- 27. Alipour, M. and Rostamy, D. (2011) Bernstein Polynomials for Solving Abel’s Integral Equation. The Journal of Mathematics and Computer Science, 3, 403-412.












