Received 23 July 2015; accepted 27 March 2016; published 30 March 2016

ABSTRACT

In this paper, we proved some fixed point theorems in intuitionistic fuzzy metric spaces applying the properties of weakly compatible mapping and satisfying the concept of implicit relations for t norms and t connorms.

Keywords:

Intuitionistic Fuzzy Metric Spaces, Weakly Compatible Mapping Implicit Relations for t Norms and t Connorms

1. Introduction

The concept of fuzzy sets is introduced by Zadeh [1] . In 1975, Kramosil and Michlek [2] introduced the concept of Fuzzy sets, Fuzzy metric spaces. George and Veeramani [3] gave the modified version of fuzzy metric spaces using continuous t norms. In 2005, Park, Kwun and Park [4] proved some point theorems “intuitionistic fuzzy metrics spaces”. In 1986, Jungck [5] introduced concept of compatible mappings for self mappings. Lots of the theorems were proved for the existence of common fixed points in classical and fuzzy metric spaces. Aamri and Moutawakil [6] introduced the concept of non-compatibility using E. A. property and proved several fixed point theorems under contractive conditions. Atanassove [7] introduced the concept of intuitionistic fuzzy sets which is a generalization of fuzzy sets.

In 2004, Park [8] defined intuitionistic fuzzy metric spaces using t-norms and t conorms as a gerenelization of fuzzy metric spaces. Turkoglu [9] gerenelized Junkck common fixed point theorem to intuitionistic fuzzy metric spaces. In this paper, we used E. A. property in intuitionistic fuzzy metric spaces to prove fixed point theorems for a pair of selfmaps. Kumar, Bhatia and Manro [10] proved common fixed point theorems for weakly maps satisfying E. A. property in “intuitionistic fuzzy metrics spaces” using implicit relation.

In this paper, we proved fixed point theorems for weakly compatible mappings satisfying E. A. property in “intuitionistic fuzzy metrics spaces” using implicit relation.

2. Preliminaries

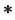Definition 1.1 (t norms). A binary operation is a continuous t norms if satisfies the following axioms:

1) is commutative as well as associative

2) 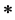is continuous

3)

4) 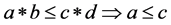and,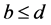

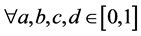
Definition 1.2 (t conorms). A binary operation 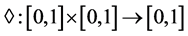is a continuous t conorms if 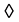satisfies the following axioms:

1) 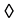is commutative as well as associative

2) is continuous

3)

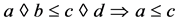4) and,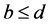

Alaca [11] generalized the Fuzzy metric spaces of Kramosil and Michlek [2] and defined intuitionistic fuzzy metric spaces with the help of continuous t-norms and t conorms as:

Definition 1.3 (intuitionistic fuzzy metric spaces). A 5-tuple is said to be intuitionistic fuzzy metric spaces if X is a arbitrary set, and are t-norms and t conorms respectively and M and N are fuzzy sets on satisfying the following axioms:

1) and

2)

3) and iff

4) and

5) and

6) is left continuous

7) and

8)

9) and iff

10) and

11) and

12) is right continuous

13) and

Then is called an intuitionistic fuzzy metric spaces on x. The functions and define the degree of nearness and degree of non-nearness between x and y with respect to respectively.

Proposition 1.4. Every fuzzy metric space is an Intuitionistic fuzzy space of the form if and are associate as

Proposition 1.4. In intuitionistic fuzzy metric spaces, is increasing and is decreasing.

Lemma 1.5. Let be an intuitionistic fuzzy metric spaces. Then

1) A sequence in X is convergent to a point if, for

and

2) A sequence in X is Cauchy sequence if, for and

and

3) An intuitionistic fuzzy metric spaces is said to be complete if every Cauchy sequence in X is convergent.

Example 1.6. Consider, and continuous t norm and continuous t conorm as

, and. If and, is defined as

and

Then is complete intuitionistic fuzzy metric spaces.

Proposition 1.7. A pair of self mappings of an intuitionistic fuzzy metric space is called commuting if

and

Proposition 1.8. A pair of self mappings of an intuitionistic fuzzy metric space is called weakly compatible if they commute at coincidence point i.e., for we have, then.

Proposition 1.9. A pair of self mappings of an intuitionistic fuzzy metric space is said to satisfy E. A. property if there exist a sequence of x such that

and.

3. Implicit Functions

Popa [12] defined the concept of implicit function in proving of fixed point theorems in hybrid metric spaces. Implicit function can be described as, let ∅ be the family of lower semi-continuous functions satisfying the following conditions:

G₁: F is non-increasing in variables and non-decreasing in

G₂: and with, such that and

G₃:,

Popa [12] defined the following examples of implicit function too,

Example 2.1. Let as

where.

Example 2.2. Let as

where,.

Example 2.3. Let as

where.

Example 2.4. Let as

,

where

M. Imdad and Javed Ali [13] - [15] added some implicit functions to prove fixed point theorems for Hybrid contraction. Following are examples are as:

Example 2.5. Let as

where.

Example 2.6. Let as

where.

Example 2.7. Let as

,

where, and.

If be an intuitionistic fuzzy metric space. Continuous t-norms and t conssorms are defined as and respectively, where.

Then implicit functions can be defined as are mappings and upper semi-continuous, non- decreasing, such that, then

(F₁)

(F₂)

(F₃)

Example 2.8. are mappings and upper semi-continuous, non-decreasing, such that, then

(F₁)

(F₂)

(F₃), and

Example 2.9. are mappings and upper semi-continuous, non-decreasing, such that, then

(F₁)

(F₂)

(F₃), and

Example 3.0. are mappings and upper semi-continuous, non-decreasing, such that, then

(F₁)

(F₂)

(F₃) and

4. Main Result

Theorem 3.1. Let be an intuitionistic fuzzy metric space. Continuous t norms and t conorms are defined as and respectively, where. Let T and S be two weakly compatible maps of X satisfying the following conditions:

(3.1.1) T and S satisfying E.A. properties,

(3.1.2) S is the closed subspaces of X,

(3.1.3), , , there is, such that

where are mappings and upper semi-continuous, non-decreasing, such that

and

Then S and T have a common fixed point.

Proof. From (3.1.1), we have a sequence in X such that

for some. From (3.1.2), is the closed subspace of X ⇒ there is such that.

Therefore. Now our goal is to prove.

In (3.1.3), taking and, we have

Taking, we have

Since

Similarly

Taking, we have

Since

Hence (say) ⇒ v is a coincident point of T and S.

Again T and S are compatible mappings, therefore.

Now we are to show that v is common point of T and S. Therefore replacing x and y by z and v in (3.1.3), we have

Since

Similarly

Since

is a common fixed point for T and S.

Uniqueness of the point will be proved by contradiction. For that suppose p and q be two fixed points. Therefore from (3.1.3) we have

Since

Similarly

Since

Hence mappings T and S have a unique fixed point.

This completes the proof.

Theorem 3.2. Let 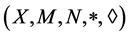be an intuitionistic fuzzy metric space. Continuous t norms and t con- orms are defined as and respectively, where.

Let T and S be two weakly compatible maps of X satisfying the following conditions:

(3.2.1) T and S satisfying E.A. properties,

(3.2.2) S is the closed subspaces of X,

(3.2.3), , such that

where are mappings and upper semi-continuous, non-decreasing, such that

(3.2.4) and

Then S and T have a common fixed point.

Proof. From (3.2.1), we have a sequence 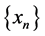in X such that

for some. From (3.2.2), is the closed subspace of X ⇒ there is such that.

Therefore Now our goal is to prove.

In (3.2.3), taking and, we have

Taking we have,

(3.2.5)

Similarly

Taking we have

(3.2.6)

(3.2.5) and (3.2.6) both are the contradiction of (3.2.4).

Hence (say) ⇒ v is a coincident point of T and S. Again T and S are compatible mappings, therefore.

Now we are to show that v is common point of T and S. Therefore replacing x and y by z and v in (3.2.3), we have

This is a contradiction. Similarly

This is a contradiction again. Hence ⇒ z is a common fixed point for T and S.

Uniqueness of the point will be proved by contradiction. For that suppose p and q be two fixed points.

Therefore from (3.2.3), we have

Similarly

This is the contradiction of (3.2.4).

. Hence mappings T and S have a unique fixed point.

This completes the proof.

Cite this paper

Arun Garg,Zaheer K. Ansari,Pawan Kumar, (2016) Fixed Point Theorems in Intuitionistics Fuzzy Metric Spaces Using Implicit Relations. Applied Mathematics,07,569-577. doi: 10.4236/am.2016.76052

References