Received 16 July 2015; accepted 21 August 2015; published 24 August 2015

ABSTRACT

The purpose of this paper is to define the concept of mixed saddle point for a vector-valued Lagrangian of the non-smooth multiobjective vector-valued constrained optimization problem and establish the equivalence of the mixed saddle point and an efficient solution under generalized (V, r)-invexity assumptions.

Keywords:

Nonsmooth Multiobjective Programs, (V, r)-Invexity, Mixed Saddle Point, Vector-Valued Mixed Lagrangian Function

1. Introduction

Jeyakumar and Mond [1] have introduced the notion of V-invexity for vector function and discussed its application to a class of multiobjective problems. Mishra and Mukherjee [2] and Liu [3] extended the concept of V-invexity of multiobjective programming to the case of nonsmooth multiobjective programming problems and duality results are also obtained. Jeyakumar [4] introduced r-invexity for differentiable scalar-valued functions. Also, Jeyakumar [5] defined r-invexity for nonsmooth scalar-valued functions, studied duality theorems for nonsmooth optimization problems, and gave relationship between saddle points and optima. In [6] (Bector), a sufficient optimality theorem is proved for a certain minmax programming problem under the assumptions (B, h)-invexity conditions.

Kuk, Lee and Kim [7] discussed that weak vector saddle-point theorems are obtained under V-r-invexity for vector-valued functions. Bhatia and Garg [8] defined (V, r)-invexity, (V, r)-quasiinvexity and (V, r)-pseudo- invexity for nonsmooth vector-valued Lipschitz functions using Clarke’s generalized subgradients and established duality results for multiobjective programming problems. Bhatia [9] introduced higher order strong convexity for Lipschitz functions. The notion of vector-valued partial Lagrangian is also introduced and equivalence of the mixed saddle points of higher order and higher order minima are provided. In [10] -[13] , saddle point theory in terms of Lagrangian functions was introduced. In [14] (Reddy and Mukherjee), some problems consisting of nonsmooth composite multiobjective programs have been treated with (V, r)-invexity type conditions and also vector saddle point theorems were obtained for composite programs. Yuan, Liu and Lai [15] defined new vector generalized convexity.

In this paper, we define the concept of mixed saddle point for a vector-valued constrained optimization problem and establish the equivalence of the mixed saddle point and an efficient solution under generalized (V, r)- invexity assumptions. Further mixed saddle point theorems are obtained.

2. Preliminaries

In this section we require some definitions and results.

Let 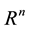be the n-dimensional Euclidean space and 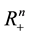be its nonnegative orthant. Throughout this paper, the following conventions for vectors in 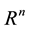will be used:

a) if and only if,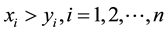

b) 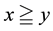if and only if,

c) 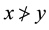is the negation of.

The following non-smooth multiobjective programming problem is studied in this paper:

where

1)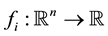, and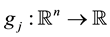, 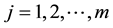are locally Lipschitz functions on.

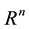2) Let be the set of feasible solution of problem (MOP). Now let and, denotes the cardinality of the index set and

clearly.

Problem (MOP) can be associated to problem:

Now, we introduce the following definitions:

Definition 1. A vector function, locally Lipschitz at, is said to be (V, r)-invex at if there exist functions, a real number ρ and such that for all for

for every and for

for every then is called strictly (V, r)-invex at.

Definition 2. A vector function, locally Lipschitz at, is said to be (V, r)-pseudoinvex at if there exist functions, a real number ρ and such that for all

for every

for every then the function is strictly (V, r)-pseudoinvex at.

Definition 3. A vector function, locally Lipschitz at, is said to be (V, r)-quasiinvex at if there exist functions, a real number ρ and such that for all

for every

If is (V, r)-invex at each then the function is (V, r)-invex on. Similar is the definition of other functions. It is evident that every (V, r)-invex function is both (V, r)-pseudoinvex and (V, r)-quasiinvex

with and

From the definitions it is clear that every strictly (V, r)-pseudoinvex on is (V, r)-quasiinvex on.

Definition 4. A feasible point is said to be efficient solution for MOP if there is no other feasible solution such that for some

and

for all.

Definition 5. The vector valued mixed Lagrangian function corresponding to problem (MOP) is defined as

where

Definition 6. A vector is said to be mixed saddle point of mixed Lagrangian if

Definition 7. A function is sublinear if for any,

1)

2) for any and.

For

Now, we have established our main results, to prove equivalence between mixed saddle point and an efficient solution.

3. Main Results

Theorem 1. Let satisfy the following conditions

(1)

(2)

(3)

(4)

Further, let be (V, r)-pseudoinvex at and is (V, r)-quasiinvex at

with Then is a mixed saddle point of.

Proof. Since satisfies (1), we have

(5)

(6)

As, from (6), we obtain

(7)

Hence, there exist

such that

(8)

Now for any

(9)

As, (9) gives

(10)

From (2) and (10) it follows that

(11)

Using the (V, r)-quasiinvexity of at, we get

(12)

(12) along with the fact gives

(13)

From (8) and (13) and using the sublinearity of, we have

(14)

(15)

Now using (V, r)-pseudoinvex of at in (15)

(16)

Since, we obtain from (16)

(17)

Again for any and we have

(18)

(18) along with (2) implies

(19)

Therefore, from (19)

(20)

Hence

(21)

From (17) and (21) and the fact that, it follows that is a mixed saddle point of.

Theorem 2. Let satisfy the conditions from (1) to (4). If is (V, r)-

quasiinvex at and is strictly (V, r)-pseudoinvex at with then is mixed saddle point.

Proof. Since satisfies (1), proceeding in the same manner as in the Theorem (1), we have

(22)

where and.

Now, for any, , which along with (2) gives

(23)

Using strict (V, r)-pseudoinvexity of at in (23) we get

(24)

The fact of and (24) gives

(25)

From the sublinearty of V

(26)

(25) along with (26) gives

(27)

From (V, r)-quasiinvexity of at and (27) it follows that

(28)

From (28), proceeding in the same manner as in Theorem (1) we obtain that is the mixed saddle point of.

Theorem 3. Let be an efficient solution for the problem (MOP) and let the functions be regular at. Assume that for at least one r, (MOP_r) is calm at. Then there exit and such that

satisfies conditions from (1) to (4). Further let be strictly (V, r)-pseudoinvex at

and be (V, r)-quasiinvex at with then is a mixed saddle point of.

Proof. Since is an efficient solution of (1) and Clarke’s calmness constraint qualification holds. It follows from Fritz John type necessary optimality conditions that, such that

(29)

(30)

(31)

Now as are regular at, (29) gives

(32)

(30), (31) and (32) imply that conditions (1) to (4) are satisfied. As satisfies (1) to (4), proceeding in the same manner as in Theorem (1), we obtain (15).

Now, using strict (V, r)-pseudoinvexity of at, we get

(33)

Since, , we obtain from (33)

Again, proceeding in the same manner as in Theorem (1), it is proved that is a mixed saddle point of.

In the next theorem no invexity or generalized invexity is used.

Theorem 4. If is a mixed saddle point of mixed Lagrangian then is an efficient solution of the problem (MOP).

Proof: Since is a mixed saddle point of, we have and

(34)

From (34), we get

(35)

Taking in (35), where is a vector having unity at the position and zero elsewhere, we get

Moreover, hence

(36)

Thus, we have

Hence, is feasible for the problem (MOP). Further, taking in (35), we get

(37)

But as and, from (37), we obtain

(38)

Now contrary to the result, let be not an efficient solution of the problem (MOP). Then there exist and an index, such that

(39)

and

(40)

(39) and (40) along with (38) give

(41)

and

(42)

that is

(43)

(44)

(43) and (44) are contradiction to the fact that

Acknowledgements

The research work presented in this paper is supported by grants to the first author from “University Grants Commission, New Delhi, India”, Sch. No./JRF/AA/283/2011-12.

Cite this paper

ArvindKumar,Pankaj KumarGarg, (2015) Mixed Saddle Point and Its Equivalence with an Efficient Solution under Generalized (V, p)-Invexity. Applied Mathematics,06,1630-1637. doi: 10.4236/am.2015.69145

References