Applied Mathematics
Vol.06 No.06(2015), Article ID:56920,7 pages
10.4236/am.2015.66093
Common Fixed Points for Two Contractive Mappings of Integral Type in Metric Spaces
Xing Jin, Yongjie Piao*
Department of Mathematics, College of Science, Yanbian University, Yanji, China
Email: *sxpyj@ybu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 May 2015; accepted 2 June 2015; published 5 June 2015
ABSTRACT
In this paper, we obtain unique common fixed point theorems for two mappings satisfying the variable coefficient linear contraction of integral type and the implicit contraction of integral type respectively in metric spaces.
Keywords:
Contractive Mapping of Integral Type, Common Fixed Point, Metric Space

1. Introduction and Preliminaries
Throughout this paper, we assume that 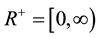 and
and 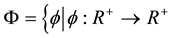 satisfying that
satisfying that 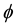 is Lebesgue
is Lebesgue
integral, summable on each compact subset of 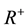 and
and 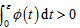 for each
for each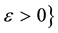 .
.
The famous Banach’s contraction principle is as follows:
Theorem 1.1 ([1] ). Let f be a self mapping on a complete metric space 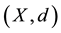 satisfying
satisfying
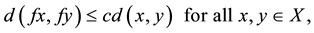 (1.1)
(1.1)
where 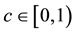 is a constant. Then f has a unique fixed point
is a constant. Then f has a unique fixed point 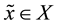 such that
such that 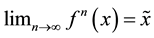 for each
for each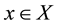 .
.
It is known that the Banach contraction principle has a lot of generalizations and various applications in many directions; see, for examples, [2] - [15] and the references cited therein. In 1962, Rakotch [11] extended the Banach contraction principle with replacing the contraction constant c in (1.1) by a contraction function 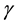 and obtained the next theorem.
and obtained the next theorem.
Theorem 1.2 ( [11] ). Let f be a self-mapping on a complete metric space 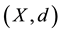 satisfying
satisfying
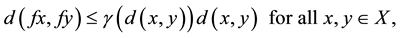 (1.2)
(1.2)
where 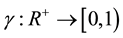 is a monotonically decreasing function. Then f has a unique fixed point
is a monotonically decreasing function. Then f has a unique fixed point 


In 2002, Branciari [12] gave an integral version of Theorem 1.1 as follows.
Theorem 1.3 ( [12] ). Let f be a self-mapping on a complete metric space 

where 



In 2011, Liu and Li [13] modified the method of Rakotch to generalize the Branciari’s fixed point theorem with replacing the contraction constant c in (1.3) by contraction functions 

Theorem 1.4 ([13] ). Let f be a self-mapping on a complete metric space 

where 






Then f has a unique fixed point 


Here, we will use the methods in [3] [9] [13] to discuss the unique existence problems of common fixed points for two self-mappings satisfying two different contractive conditions of integral type in a complete metric space.
2. Common Fixed Point Theorems
Lemma 2.1 ([13] ). Let 



Lemma 2.2([13] ). Let 

Now, we will give the first main result in this paper.
Theorem 2.1. Let 



where 



Then f and g have a unique common fixed point u, and the sequence 



Proof.
Let






For
hence by (2.3),

Similarly, by (2.1),
hence by (2.3),

Combining (2.4) and (2.5), we have

Now, we prove that

Otherwise, there exists 

Obviously,

which is a contradiction. Similarly, if
which is also a contradiction. Hence (2.7) holds. Therefore there exists 


which is a contradiction. Therefore

We claim that 






For k, let 


hence

Let

hence we obtain

If 

which is a contradiction. Similarly, we obtain the same contradiction for the case that 




If

which is a contradiction, hence


If 

which is a contradiction, hence

From Theorem 2.1, we obtain the next more general common fixed point theorem.
Theorem 2.2. Let 




where




Proof.
Let 





which is a contradiction, hence

From now on, we will discuss the second common fixed point problem for two mappings with implicit contraction of integral type.
Let 

(i) There exists 


(ii) There exists 


(iii) 

Example 2.1. Define 
where 



The function 

Example 2.2. Let 



Hence 
Theorem 2.3. Let 



where 

Proof.
We take any element 






Since
So by (i),

Similarly,
So by (ii),

Combining (2.14) and (2.15), we have

Obviously, 





which is a contradiction. Similarly, if
which is also a contradiction. Hence we have
Therefore there exists 


which is a contradiction. Therefore, 
We claim that 






If 

This is a contradiction. Similarly, we obtain the same contradiction for the case that 



If

which is a contradiction, hence


If 

This is a contradiction. Hence 
Using Theorem 2.3 and the Example 2.2, we have the next result.
Theorem 2.4. Let 

where
Combining Theorem 2.4 and Example 2.1, we obtain the following result.
Theorem 2.5. Let 


where 


Acknowledgements
The research is partially supported by the National Natural Science of Foundation of China (No. 11361064).
References
- Banach, A. (1929) Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundamenta Mathematicae, 3, 133-181.
- Aliouche, A. (2006) A Common Fixed Point Theorem for Weakly Compatible Mappings in Symmetric Spaces Satisfying a Contractive Condition of Integral Type. Journal of Mathematical Analysis and Applications, 322, 796-802. http://dx.doi.org/10.1016/j.jmaa.2005.09.068
- Altun, I. and Türkoğlu, D. (2009) Some Fixed Point Theorems for Weakly Compatible Mapping Satisfying an Implicit Relation. Taiwanese Journal of Mathematics, 13, 1291-1304.
- Jachymski, J. (2009) Remarks on Contractive Conditions of Integral Type. Nonlinear Analysis, 71, 1073-1081. http://dx.doi.org/10.1016/j.na.2008.11.046
- Mocanu, M. and Popa, V. (2008) Some Fixed Point Theorems for Mappings Satisfying Implicit Relations in Symmetric Spaces. Libertas Mathematica, 28, 1-13.
- Gairola, U.C. and Rawat, A.S. (2008) A Fixed Point Theorem for Integral Type Inequality. International Journal of Mathematical Analysis, 2, 709-712.
- Moradi, S. and Omid, M. (2010) A Fixed Point Theorem for Integral Type Inequality Depending on Another Function. International Journal of Mathematical Analysis, 4, 1491-1499.
- Altun, I., Abbas, M. and Simsek, H. (2011) A Fixed Point Theorem on Cone Metric Spaces with New Type Contractivity. Banach Journal of Mathematical Analysis, 5, 15-24. http://dx.doi.org/10.15352/bjma/1313362998
- Popa, V. and Mocanu, M. (2009) Altering Distance and Common Fixed Points under Implicit Relations. Hacettepe Journal of Mathematics and Statistics, 38, 329-337.
- Abbas, M. and Rhoades, B.E. (2007) Common Fixed Point Theorems for Hybrid Pairs of Occasionally Weakly Compatible Mappings Satisfying Generalized Contractive Condition of Integral Type. Fixed Point Theory and Applications, 2007, Article ID: 054101. http://dx.doi.org/10.1155/2007/54101
- Rakotch, E. (1962) A Note on Contractive Mappings. Proceedings of the American Mathematical Society, 13, 459-465. http://dx.doi.org/10.1090/S0002-9939-1962-0148046-1
- Branciari, A. (2002) A Fixed Point Theorem for Mappings Satisfying a General Contractive Condition of Integral Type. International Journal of Mathematics and Mathematical Sciences, 29, 531-536. http://dx.doi.org/10.1155/S0161171202007524
- Liu, Z.Q., Li, X., Kang, S.M. and Cho, S.Y. (2011) Fixed Point Theorems for Mappings Satisfying Contractive Conditions of Integral Type and Applications. Fixed Point Theory and Applications, 2011, 64. http://dx.doi.org/10.1186/1687-1812-2011-64
- Abbas, M., Cho, Y.J. and Nazir, T. (2012) Common Fixed Points of Ćirić-Type Contractive Mappings in Two Ordered Generalized Metric Spaces. Fixed Point Theory and Applications, 2012, 139. http://dx.doi.org/10.1186/1687-1812-2012-139
- Gu, F. and Ye, H.Q. (2012) Common Fixed Point Theorems of Altman Integral Type Mappings in Metric Spaces. Abstract and Applied Analysis, 2012, Article ID: 630457. http://dx.doi.org/10.1155/2012/630457
NOTES
*Corresponding author.





























