Applied Mathematics
Vol.06 No.05(2015), Article ID:56778,12 pages
10.4236/am.2015.65080
Numerical Modelling and Simulation of Sand Dune Formation in an Incompressible Out-Flow
Yahaya Mahamane Nouri, Saley Bisso
Department of Mathematics and Informatic, Abdou Moumouni Unversity, Niamey, Niger
Email: alassanenouri@yahoo.fr, bsaley@yahoo.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 April 2015; accepted 26 May 2015; published 29 May 2015
ABSTRACT
In this paper, we are concerned with computation of a mathematical model of sand dune formation in a water of surface to incompressible out-flows in two space dimensions by using Chebyshev projection scheme. The mathematical model is formulate by coupling Navier-Stokes equations for the incompressible out-flows in 2D fluid domain and Prigozhin’s equation which describes the dynamic of sand dune in strong parameterized domain in such a way which is a subset of the fluid domain. In order to verify consistency of our approach, a relevant test problem is considered which will be compared with the numerical results given by our method.
Keywords:
Sand Dune Formation, Navier-Stokes Equations, Incompressible Out-Flows, Chebyshev Projection Scheme

1. Introduction
The sandbank is a real physical phenomenon that constitutes a threat for our environment through the occu- pation of the roads, the arable earths and especially the waters of surfaces, as it is the case of the Niger stream. The main goal of this paper is to compute numerically the height of sand dune in a water of surface to the incompressible out-flows (streams, lakes, seas, ...). For this, we formulate a mathematical model which couples the Navier-Stokes equations for the incompressible out-flows in two space dimensions and Prigozhin’s equation that describes the sand dune dynamic [1] -[3] . The numerical approach that we develop to solve this model is made in three stages. The first stage aims to approach the Navier-Stokes equations by using Chebyshev projection scheme, following 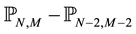 method [4] - [7] , the second stage is dedicated to the determination of the mass density of the sand grains transported by the out-flows, and we compute the dune height in the third stage.
method [4] - [7] , the second stage is dedicated to the determination of the mass density of the sand grains transported by the out-flows, and we compute the dune height in the third stage.
The outline of this paper is as follows. In Section 2, we give the problem formulation and description of parameters. In Section 3, the numerical scheme which will be used in this paper is presented. In Section 4, some numerical simulations of the solution and temporal errors evolution are presented. We end this paper with a conclusion and the perspectives in Section 5.
2. The Problem Formulation
Let 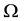 be a bounded open subset with regular boundary
be a bounded open subset with regular boundary  in
in  in which flows out a fluid to incom- pressible out-flows with a velocity u and a pressure p [6] . We suppose a sand dune isolated and completely immersed in
in which flows out a fluid to incom- pressible out-flows with a velocity u and a pressure p [6] . We suppose a sand dune isolated and completely immersed in 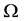 and occupying a strong subdomain
and occupying a strong subdomain  of
of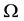 . Let denote by m and h, respectively the mass density of the sand grains transported by the out-flows and the dune height. While supposing that the mass
. Let denote by m and h, respectively the mass density of the sand grains transported by the out-flows and the dune height. While supposing that the mass
density is transported by a flux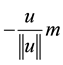 , we propose the following mathematical model to describe the inter-
, we propose the following mathematical model to describe the inter-
action between the out-flow of the fluid and the dynamics of the dune in two space dimensions given by:
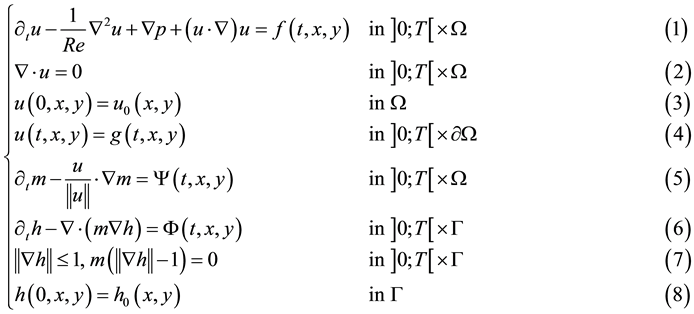
where
・ 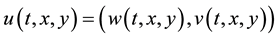 is the vector velocity, w is the component following the x-axis and v the y-axis one;
is the vector velocity, w is the component following the x-axis and v the y-axis one;
・  is the pressure;
is the pressure;
・  ,
,  and
and  are the source term;
are the source term;
・ 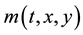 is the mass density;
is the mass density;
・  is the height of sand dune;
is the height of sand dune;
・ 
・ T is a given positive time-parameter.
The out-flow of the fluid is modelling by Equations (1)-(4). The transportation of the sand grains under the effect of averaged velocity is modelling by Equation (5). The dynamics of the sand dune is modelling by Equ- ations (6)-(8).
To ensure the regularity of the solution we suppose that the functions f, 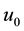
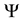
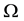


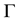
and the initial data 
where n is the unit vector normal to the boundary of the domain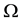
3. Numerical Schemes
3.1. Temporal Discretisation
For a given positif integer r, we consider a time step discretisation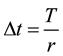
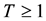
knots of the interval 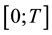
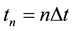
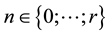
For a given continues function

In order to approach in time Equations (1)-(8), we used second-order backward Euler scheme which is given by:
While doing an extrapolation of order 1 of the pressure at the time of the prediction stage and while appro- aching the convection term 
- prediction stage:
where 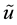
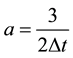

- projection stage:


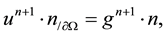
where 
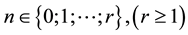
Thus, when one does a spatial discretisation of this problem by using a Chebyshev spectral method, so that the resulting discreet problem is well posed, it is necessary that the discreet spaces of velocity and pressure verify a compatibility condition inf-sup of Brezzi [11] .
To answer this question of compatibility condition, we use the spectral method 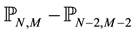
3.2. Spatial Discretisation
In this section we present the basic principle of the method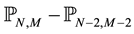
So for a given positive integers N and M we denote by 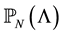

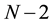
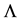
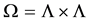
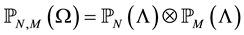
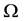

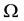

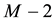
The 
In this paper, we consider Chebyshev polynomials and choose the Chebyshev-Gauss-Lobatto mesh defined by:
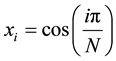
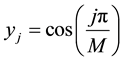
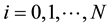

Then, we consider the velocity at 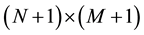


Let us making the following space approximation for
We approach the first and secondary operators of derivation of 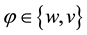
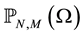
where 
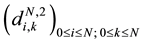
order 1 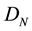
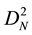

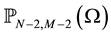
where 
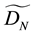

Let us consider the following approximation spaces:
where 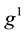
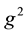
We define by:
Then the prediction stage (9)-(10) decomposes itself in two-Helmholtz problems for each components of the predicted velocity with Dirichlet boundary conditions:

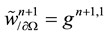

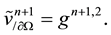
The Chebyshev collocation approximation of Helmholtz problems (15) and (17) is given by:
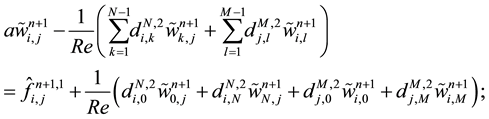
and
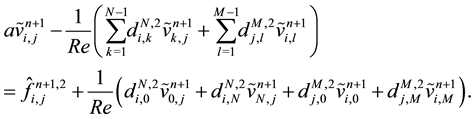
Multiplying these equations by
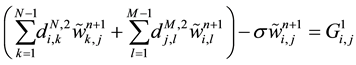
and

where
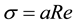

Let us denote by:
Then, we can rewrite Equations (21) and (22) by:
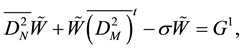
and
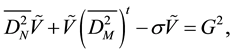


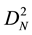
Systems (23) and (24) are solving by using diagonalisation method [10] .
Let us denote by 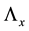
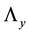
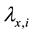
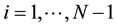
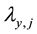
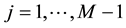

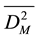
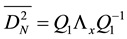
and
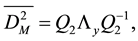
where 
Multiplying the Equation (23) on the left by

we deduce that:
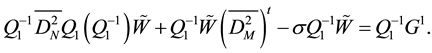
Let us denote by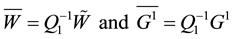
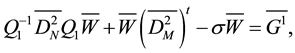
From (25) and (26), we deduce:
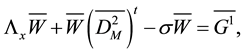
and multiplying this equation on the right by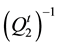
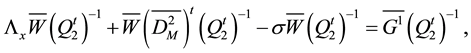
so that, we deduce the following equation:
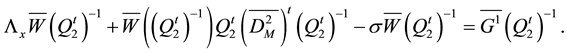
Denoting by 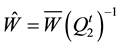
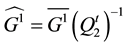
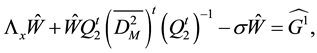
using relation (26), we obtain:
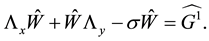
Then, we deduce:

We compute completely 
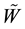
1) Compute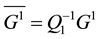
2) Compute
3) Compute 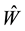
4) Compute
5) Compute
When applying the same algorithm to Equation (24), we can compute completely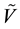
In order to make the projection stage, we define:
then we can rewrite Equations (12)-(13) by:
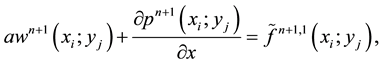
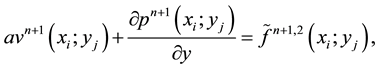
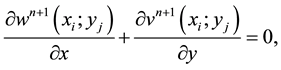
with boundary conditions:
So, while noting:
then by using spectral method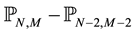

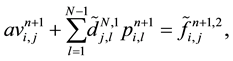
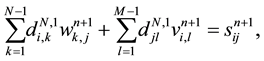
where
with boundary conditions :
Let us denote by:
Then, we obtain the following matrix formulation for Equations (39)-(41), given by:
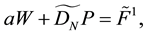
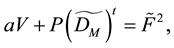
where 
Reformulating Equations (42), (43) and (44), we deduce :


where
We solve Equation (47) by using the same strategy using for solving Equation (21) and (22). Then we deter- mine completely the P matrix for the pressure and deduce the matrixes W and V containing the values of the first and the second components of velocity, respectively from Equations (45) and (46).
Let us denote by 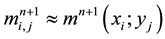
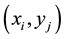

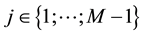
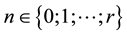
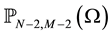
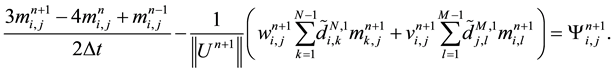
We denote by 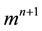
We can rewrite Equation (48) by:
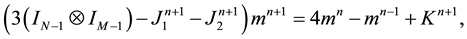
where:
where 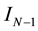
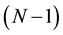

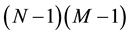
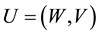
And while denoting by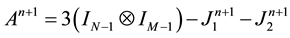
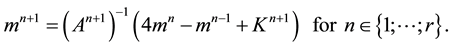
To make the approximation of Equations (6)-(8), we suppose that the strong domain occupied by sand dune is
parameterized by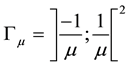
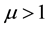
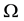
What brings us to consider another grid to approach the dune height by using new grid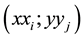
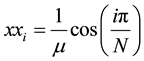
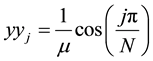
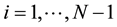

Let us denote by 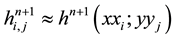
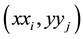
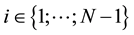

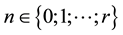
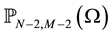
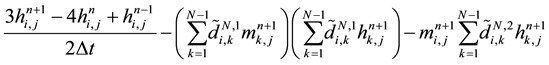
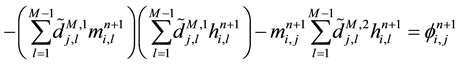
Denoting by 
we obtain the following matrix formulation:
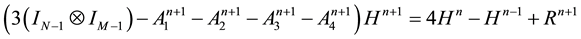
where:
and while denoting by :
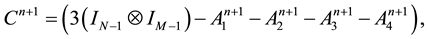

4. Numerical Result
For the numerical simulation, we consider an experimental solution on the one hand for the Navier-Stokes equations and other for the mass density and the dune height.
For example:
We take
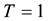
the calculated fields, we give the evolution of the temporal error 
integration in time of this error is initialized while taking the fields to the instants 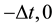
We represent temporal errors according to the first components 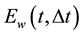
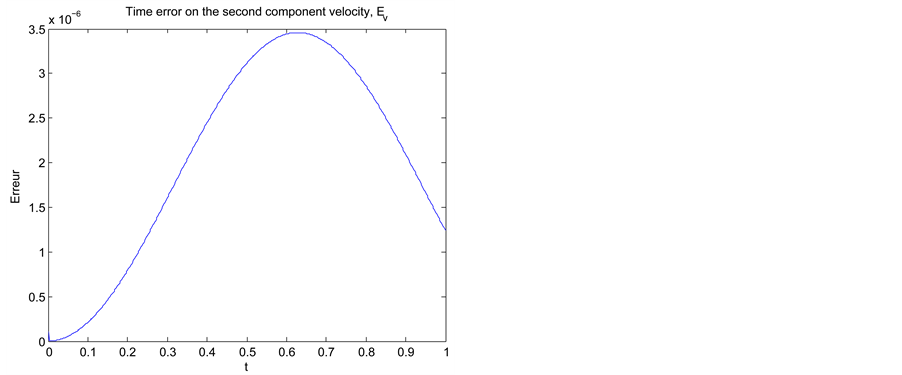
Figure 1. Temporal evolution of the errors in time on the first component of the velocity, 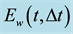
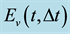
components 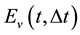
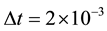

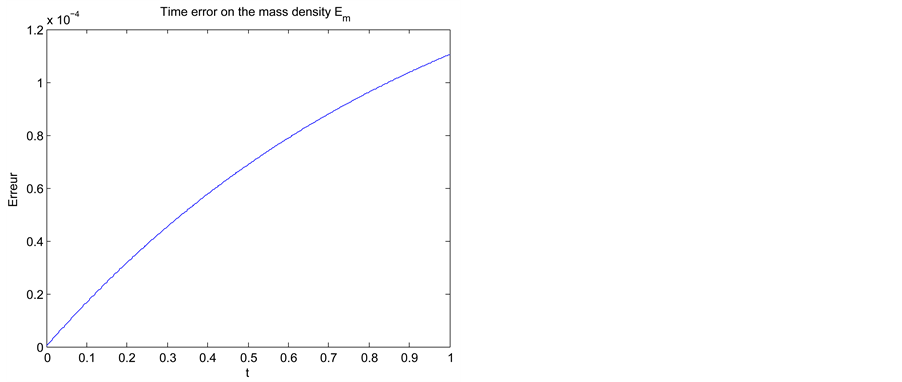
We also represent the temporal errors for the mass density of sand grains 
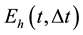


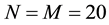
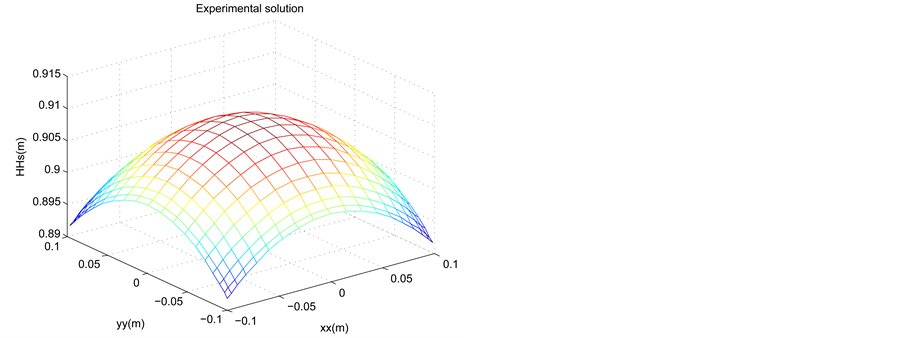
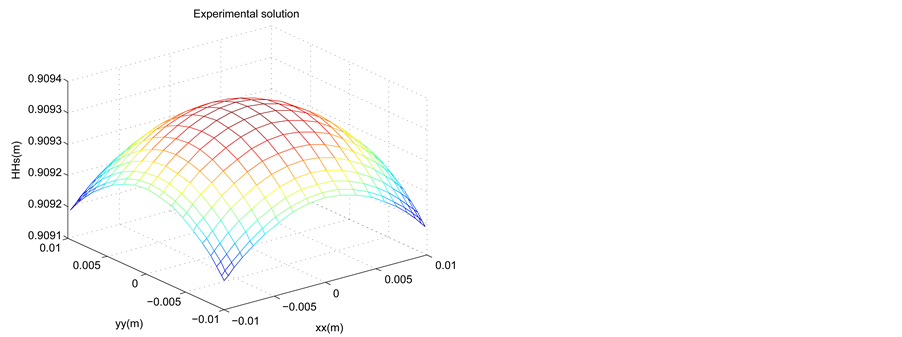
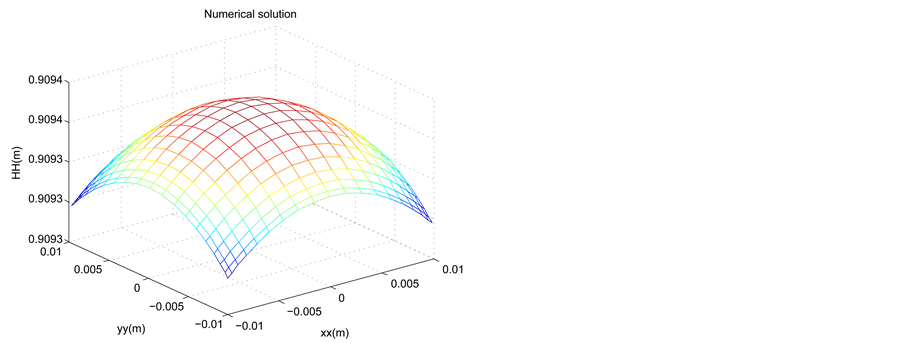
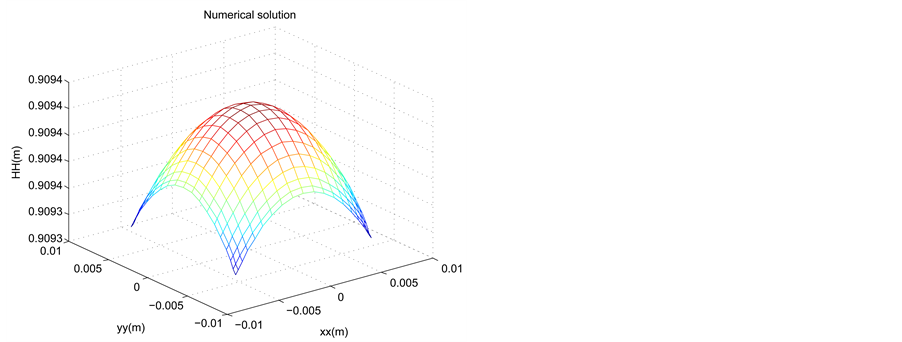
The profile of the dune height is represented at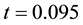
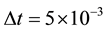

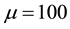
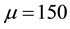
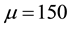
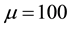
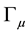
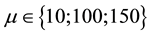
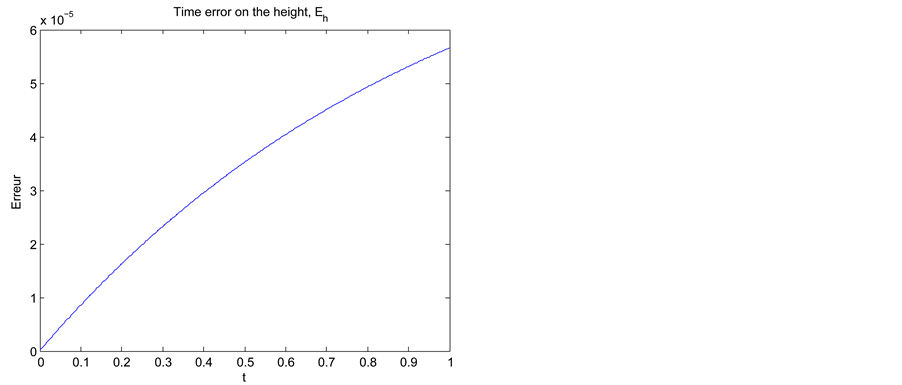
Figure 2. Temporal evolution of the errors in time on the mass density of sand grains, 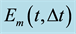
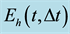
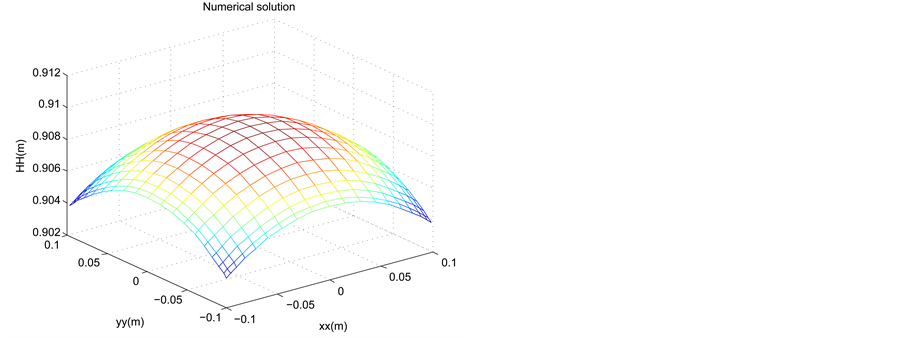
Figure 3. Profile of the experimental and approached of the dune height in the space at t = 0.095, for a time step Δt = 5 × 10−3, N = M = 20 and
Figure 4. Profile of the experimental and approached of the dune height in the space at t = 0.095, for a time stepΔt = 5 × 10−3, N = M = 20 and
Figure 5. Profile of the experimental and approached of the dune height in the space at t = 0.095, for a time step Δt = 5 × 10−3, N = M = 20 and
5. Conclusions and Perspectives
We have solved numerically a mathematical model of sand dune formation in a surface water to incompressible out-flows in two space dimensions. This model couples the Navier-Stokes equations governing the incompressi- ble out-flows in two-dimension of space and the Prigozhin equation that describes the evolution of a sand dune in a surface water. One of the difficulties of this approach resides in the treatment of the pressure which appears only in Navier-Stokes equations as Lagrange multiplier. We used a Chebyshev projection scheme following a spectral approach 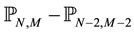
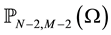

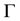
In our future works, we count to pass in dimension 3 of space and to put a optimal control in place to deter- mine the optimal height of sand dune in a surface water, from which other dunes can be formed in the fluid.
References
- Prigozhin, L. (1994) Sandpiles and River Networks: Extended Systems with Nonlocal Interactions. Physical Review E, 49, 1161. http://dx.doi.org/10.1103/physreve.49.1161
- Igbida, N. (2012) Mathematical Models for Sandpile Problems. XLIM-DMI, UMR-CNRS 6172, Workshop MathEnv, Essaouira.
- Nouri, Y.M. and Bisso, S. (2013) Numerical Approach for Solving a Mathematical Model of Sand Dune Formation. Pioneer Journal of Advances in Applied Mathematics, 9, 1-15.
- Rønquist, E.M. (1990) Optimal Spectral Element Methods for the Unsteady 3-Dimensionnal Incompressible Navier-Stokes Equations. Ph.D. Thesis, Mass, Cambridge.
- Azaez, M. (1990) Computation of the Pressure in the Stokes Problem for Incompressible Viscous Fluids by a Spectral Method Collocation. Thesis of Doctorate, Paris-Sud University, Orsay.
- Botella, O. (1996) Resolution des equations de Navier-Stokes par des schemas de Projection Tchebychev. Rapport de recherche No. 3018 de L’Institut national de rechercheen informatique et en automatique (inria).
- Maday, Y., Patera, A.T. and Rønquist, E.M. (1992) The
Method for the Approximation of the Stokes Problem. Laboratoire d’Analyse Numerique, Paris VI, 11, fasc.4.>http://html.scirp.org/file/12-7402713x290.png" class="200" /> Method for the Approximation of the Stokes Problem. Laboratoire d’Analyse Numerique, Paris VI, 11, fasc.4.
- Chorin, A. (1968) Numerical Simulation of the Navier-Stokes Equations. Mathematics of Computation, 22, 745-762. http://dx.doi.org/10.1090/S0025-5718-1968-0242392-2
- Temam, R. (1969) On the Approximation of the Solution of Navier-Stokes Equations by the Fractional Steps Method II. Archive for Rational Mechanics and Analysis, 32, 377-385.
- Azaez, M., Bernardi, C. and Grundmann, M. (1994) Spectral Methods Applied to Porous Media Equations. East-West Journal of Numerical Mathematics, 2, 91-105.
- Brezzi, F. (1974) On the Existence, Uniqueness and Approximation of Saddle-Point Problems Arising from Lagrangian Multipliers. R.A.I.R.O, R2, 129-151.
- Hesthaven, J.S., Gottlieb, S. and Gottlieb, D. (2007) Spectral Methods for Time-Dependent Problems. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511618352
- Trefethen, L.N. (2000) Spectral Methods in MATLAB. http://dx.doi.org/10.1137/1.9780898719598
- Canuto, C., Bernardi, C. and Maday, Y. (1986) Generalized Inf-Sup Condition for Chebyshev Approximation of the Navier-Stokes Equations. Technical Report, No. 86-61, ICASE.
- Canuto, C., Hussaini, M.Y., Quarteroni, A. and Zang, T.A. (1988) Spectral Methods in Fluid Dynamics. Springer- Verlag, New York. http://dx.doi.org/10.1007/978-3-642-84108-8
- Ehrenstein, U. and Peyret, R. (1989) A Chebyshev-Collocation Method for the Navier-Stokes Equations with Application to Double-Diffusive Convection. International Journal for Numerical Methods in Fluids, 9, 427-452. http://dx.doi.org/10.1002/fld.1650090405
- Azaez, M., Fikri, A. and Labrosse, G. (1994) A Unique Grid Spectral Solver of the nd Cartesian Unsteady Stokes System. Illustrative Numerical Results. Finite Elements in Analysis and Design, 16, 247-260. http://dx.doi.org/10.1016/0168-874X(94)90068-X


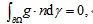
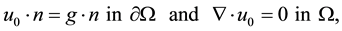

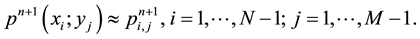
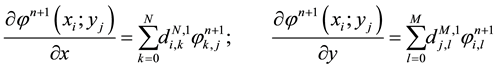
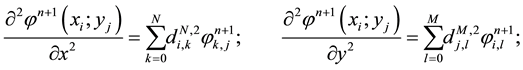
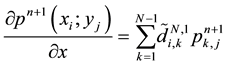

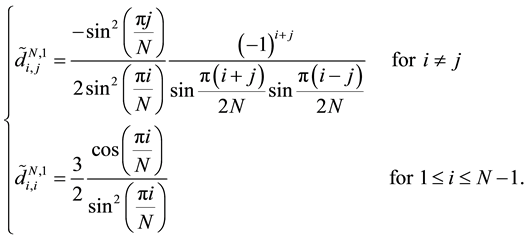

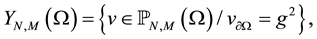
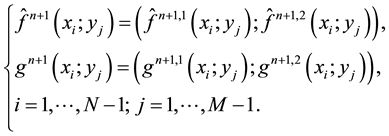
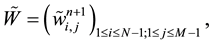
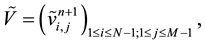
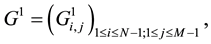

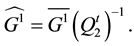
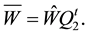
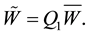

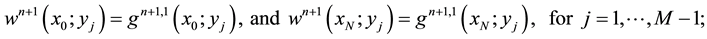
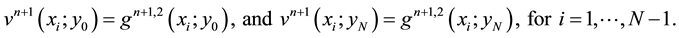
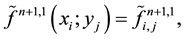

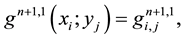
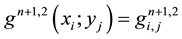

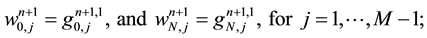
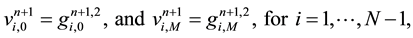

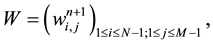
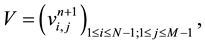
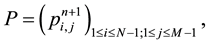
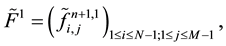
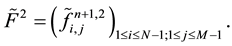

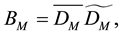
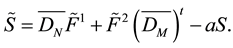
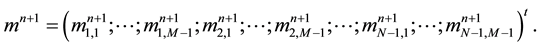


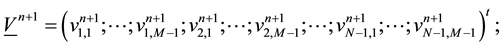
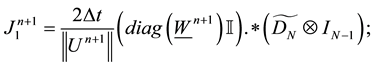
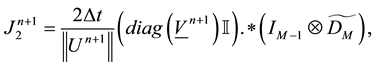
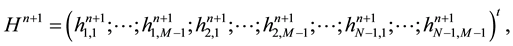
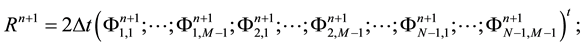
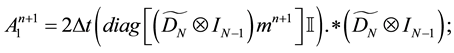
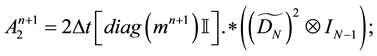


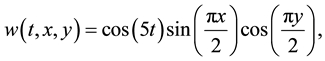




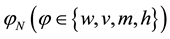


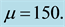
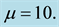

 Method for the Approximation of the Stokes Problem. Laboratoire d’Analyse Numerique, Paris VI, 11, fasc.4.>http://html.scirp.org/file/12-7402713x290.png" class="200" /> Method for the Approximation of the Stokes Problem. Laboratoire d’Analyse Numerique, Paris VI, 11, fasc.4.
Method for the Approximation of the Stokes Problem. Laboratoire d’Analyse Numerique, Paris VI, 11, fasc.4.>http://html.scirp.org/file/12-7402713x290.png" class="200" /> Method for the Approximation of the Stokes Problem. Laboratoire d’Analyse Numerique, Paris VI, 11, fasc.4.