ABSTRACT

The Poisson process is a stochastic process that models many real-world phenomena. We present the definition of the Poisson process and discuss some facts as well as some related probability distributions. Finally, we give some new applications of the process.

Keywords:

Poisson Processes, Gamma Distribution, Inter-Arrival Time, Marked Poisson Processes

1. Introduction

Poisson process is used to model the occurrences of events and the time points at which the events occur in a given time interval, such as the occurrence of natural disasters and the arrival times of customers at a service center. It is named after the French mathematician Siméon Poisson (1781-1840). In this paper, we first give the definition of the Poisson process (Section 2). Then we stated some theroems related to the Poisson process (Section 3). Finally, we give some examples and compute the relevant quantities associated with the process (Section 4).

2. What Is Poisson Process?

A Poisson process with parameter (rate) 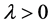is a family of random variables 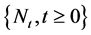satisfying the following properties:

1).

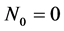2) 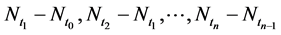are independent random variables where.

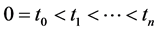3) 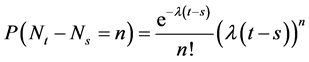for.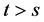

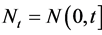can be thought of the number of arrivals up to time t or the number of occurrences up to time t.

3. Some Facts about the Poisson Process

We give some properties associated with the Poisson process. The proofs can be found in [1] or [2] . If we let 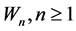be the time of the 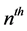arrival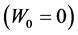, and we let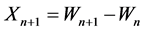, , 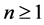be the interarrival time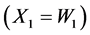. Then we have the following theorems:

Theorem 1 The 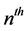arrival time has the 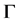-distribution with density function, for

Theorem 2 The interarrival times are independently exponentially distributed random variables with parameter.

Theorem 3 Conditioned on, the random variables have the joint density probability function

Theorem 4 If is a random variable associated with the event in a Poisson process with parameter. We assume that are independent, independent of the Poisson process, and share the common distribution function. The sequence of pairs is called a marked Poisson process. The form a two-dimensional nonhomogeneous Poisson point process in the plane, where the mean number of points in a region is given by

The marked Poisson processes have been applied in some geometric probability area [3] .

4. Examples of Poisson Processes

1) Suppose the number of calls to a phone number is a Poisson process with parameter and is the duration of each call. It is reasonable to assume that is independent of the Poisson process. What is the probability that the call gets a busy signal, i.e. it comes when the user is still responding to the call?

For a fixed,

2) On average, how many calls arrive when the user is on the phone?

Suppose the user is talking on the call,

3) In a single server system, customers arrive in a bank according to a Poisson process with parameter and each customer spends time with the one and only one bank teller. If the teller is serving a customer, the new customers have to wait in a queue till the teller finishes serving. How long on average does the teller serves the customers up to time? (i.e. How long is the server unavailable?)

4) Suppose team A and team B are engaging in a sport competition. The points scored by team A follows a Poisson process with parameter and the points scored by team B follows a Poisson process with parameter. Assume that and are independent, what is the probability that the game ties? Team A wins? Team B wins?

Let be the duration of the competition.

5) Given that there are points scored in a match (by both team A and team B), what is the probability that team A scores points, where?

6) When does a car accident happen? Suppose a street is from west to east and another is from south to north, the two streets intersect at a point. Cars going from west to east arrives at follows a Poisson process with parameter and cars going from south to east arrives at follows a Poisson process with parameter. It is reasonable to assume that these two processes are independent. If the cars don’t slow down and stop at the intersection, then collision happens. The car going from south to north hits the car going from south to east if and only if, where is the time it takes for the car's tail to reach, has density function.

7) Occurrences of natural disasters follow a Poisson process with parameter. Suppose that the time it takes to recover and rebuild after the disaster is, assume that are independent random variables having the common distribution functions. There are disasters up to time, what is the probability that everything is back to normal at time? This can also be used as a model for insurance claims. is the time for the insurance company to receive the claim and is the time the insurance company takes to settle it. What is the probability that the insurance company is not working on any claim at time?

where are independent and uniformly distributed on.

8) Suppose that is the time an insurance company receives the claim and is the time the company takes to settle the claim. What is the average time to settle all claims received before time?

The average time to settle all claims received before is

Suppose,

where are independent and uniformly distributed on.

Clearly, for.

9) Customers arrive at a shopping mall follows a Poisson process with parameter. The time the customers spend in the store are independent random variables having the common distribution function. Let be the number of customers exist up to the closing time. What is the expected number of customers in the mall at time?

Condition on and let be the arrival time of the customers. Then customer exists in the mall at time if and only if. Let the random variable

Then if and only if the customer exists in the mall at time. Thus

where are independent and uniformly distributed on. is the binomial distribution in which

Hence,

That is, the number of customers existing at time has a Poisson distribution with mean

The average number of customers exist at the mall closing time is

10) Customers arriving at a service counter follows a Poisson process with parameter. Let be the number of customers served longer than up to time. What is the distribution of?

Condition on and let be the arrival time of the customers. Let the random variable

Then if and only if the customer served longer than. Thus

which is the binomial distribution with. Hence,

That is, the number of customers served longer than has a Poisson distribution with mean

5. Conclusion

Poisson process is one of the most important tools to model the natural phenomenon. Some important distributions arise from the Poisson process: the Poisson distribution, the exponential distribution and the Gamma distribution. It is also used to build other sophisticated random process.

Cite this paper

Kung-Kuen Tse, (2014) Some Applications of the Poisson Process. Applied Mathematics,05,3011-3017. doi: 10.4236/am.2014.519288

References