Applied Mathematics
Vol.5 No.13(2014), Article
ID:47783,13
pages
DOI:10.4236/am.2014.513189
Entrance Region Flow of Herschel-Bulkley Fluid in an Annular Cylinder
Rekha G. Pai1, A. Kandasamy2
1Department of Mathematics, Manipal Institute of Technology, Manipal, India
2Department of M.A.C.S., N.I.T.K., Mangalore, India
Email: pai.rekha@manipal.edu, kandy@nitk.ac.in
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 April 2014; revised 10 June 2014; accepted 22 June 2014
ABSTRACT
The entrance region flow of a Herschel-Bulkley fluid in an annular cylinder has been investigated numerically without making prior assumptions on the form of velocity profile within the boundary layer region. This velocity distribution is determined as part of the procedure by cross sectional integration of the momentum differential equation for a given distance z from the channel entrance. Using the macroscopic mass and momentum balance equation, the entrance length at each cross section of the entrance region of the annuli and pressure distribution have been calculated for specific values of Herschel-Bulkley number and various values of aspect ratio and flow behavior index. The effects of non-Newtonian characteristics and channel width on the velocity profile, pressure distribution and the entrance length have been discussed.
Keywords:Annular Cylinder, Boundary Layer Region, Entrance Region Flow, Herschel-Bulkley Fluid, Momentum Integral Equation

1. Introduction
The entrance region flow in channels constitutes a problem of fundamental interest in engineering applications such as nuclear reactors, polymer processing industries, haemodialyzers and capillary membrane oxygenators. In such installations, the behavior of the fluid in the entrance region may play a significant part in the total length of the channel and the pressure drop may be markedly greater than for the case where the flow is regarded as fully developed throughout the channel. Recently, there has been an increasing interest in problems involving materials with variable viscosity such as Bingham materials, Casson fluids and Herschel-Bulkley fluids which are characterized by a yield value.
Batra and Bigyani Jena [1] investigated stress-strain relation in the entrance region of annuli using blood as Casson fluid. Tandon et al. [2] analyzed the blood flow in the arteries by assuming it as Casson model. Dash et al. [3] have analyzed steady and pulsatile flow considering pressure gradient as a function of time in a narrow catheterized artery taking into account blood as Casson fluid. Ramesh Gupta [4] has considered a constant property of viscous fluid entering a conduit under appropriate intake conditions so that its velocity is practically constant over the entry cross-section. Maia and Gasparetto [5] applied finite difference method for the Power-law fluids in the annuli and found difference in entrance geometries. Sankar and Hemalatha [6] have studied the pulsatile flow of blood through catheterized artery by modeling blood as Herschel-Bulkley fluid and considering artery as coaxial circular cylinders. Poole and Chhabra [7] reported the results of a systematic numerical investigation of developing laminar pipe flow of yield stress fluids. Recently Kandasamy and Pai [8] have investigated the Core variation in the entrance region flow of Casson Fluid in an annuli.
The purpose of the present work is to analyze numerically the entrance region flow of a Herschel-Bulkley fluid through annular cylinder without making assumptions in the form of velocity profile within the boundary layer. The velocity distribution is determined as part of the procedure by cross-sectional integration of the momentum differential equation for a given distance z from the channel entrance. Using macroscopic mass and momentum balances, the change in the velocity profile and pressure gradient downstream are calculated numerically. Considering the fluid flow being symmetric about the axis of the channel, the entrance length, velocity distribution and the pressure drop have been calculated in the upper portion of the annuli at each cross section of the entrance region of the channel for various values of Herschel-Bulkley number, flow behavior index and aspect ratio.
Using macroscopic mass and momentum balances, the change in the velocity profile and pressure gradient downstream are calculated numerically. Considering the fluid flow being symmetric about the axis of the channel, the entrance length, velocity distribution and the pressure drop have been calculated in the upper portion of the annuli at each cross section of the entrance region of the channel for various values of Herschel-Bulkley number, flow behavior index and aspect ratio.
2. Analysis
We are analyzing the entrance region flow of a Herschel-Bulkley fluid through an annular cylinder without making assumptions in the form of velocity profile within the boundary layer. Fluid enters a horizontal annular duct from a large chamber with a uniform velocity along the axial direction. The analysis has been carried out over the wide range of aspect ratios, that is, the ratio of the radius of the inner cylinder to that of the outer cylinder. The development of boundary layer is visualized when the fluid enters an annulus and the fully developed velocity profile is observed in the region starting from the point down-stream where the boundary layers meet asymptotically with the outer edge of the plug flow zone.
We consider a horizontal annular duct consisting of inner cylinder of radius  and outer cylinder of radius
and outer cylinder of radius 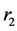 as shown in Figure 1. The Herschel-Bulkley fluid enters from a large chamber to this duct with a steady, laminar incompressible and isothermal flow with velocity
as shown in Figure 1. The Herschel-Bulkley fluid enters from a large chamber to this duct with a steady, laminar incompressible and isothermal flow with velocity 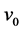 and pressure
and pressure 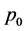 into annular boundary. We use cylindrical polar coordinate system
into annular boundary. We use cylindrical polar coordinate system  with axial symmetry and origin at the center of the cylinders at the inlet with
with axial symmetry and origin at the center of the cylinders at the inlet with 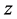 axis coinciding with the axis of the cylinders.
axis coinciding with the axis of the cylinders.  is the velocity component in r direction,
is the velocity component in r direction, 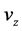 is the velocity in the
is the velocity in the 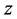 direction. Since Herschel-Bulkley fluid possesses a yield value, there is a plug core
direction. Since Herschel-Bulkley fluid possesses a yield value, there is a plug core
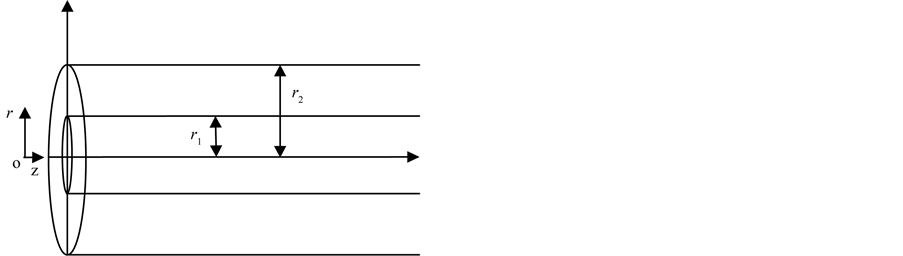
Figure 1. Geometry of an annuli.
formation away from the walls. On each wall, there is boundary layer formation separated by the core as shown in Figure 2. As the two regions about the axis are symmetrical, the solution of the problem will be considered in the upper half only. We have inner boundary layer region  with thickness
with thickness 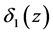 and outer boundary layer region
and outer boundary layer region 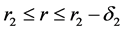 with thickness
with thickness 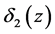 and the plug flow region
and the plug flow region 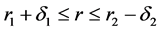 separating the two boundary layers, where the core is moving with constant velocity. In the plug core region, the shear stress
separating the two boundary layers, where the core is moving with constant velocity. In the plug core region, the shear stress 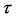 is less than or equal to the yield stress
is less than or equal to the yield stress  and the velocity at each cross section is constant. Under the assumptions of boundary layer theory and neglecting inertia terms, the equation of motion of an isotropic, incompressible fluid can be given as,
and the velocity at each cross section is constant. Under the assumptions of boundary layer theory and neglecting inertia terms, the equation of motion of an isotropic, incompressible fluid can be given as,
 (1)
(1)
where “p” is the pressure of the fluid.
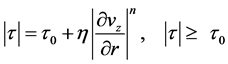 (2)
(2)
where ![]() represents coefficient of viscosity for Herschel-Bulkley fluid and “n” is the flow behavior index.
represents coefficient of viscosity for Herschel-Bulkley fluid and “n” is the flow behavior index.
Equations (1) and (2) will be solved under the following boundary conditions:
1) The axial velocity components are zero at the wall, i.e.,
 (3a)
(3a)
2) At the edge of the boundary layers,  is equal to the plug core velocity, i.e.,
is equal to the plug core velocity, i.e.,
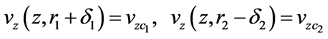 (3b)
(3b)
3) The shear stress at the edge of the lower and upper boundary of the plug core region are equal to  and
and  respectively. Hence Equation (2) reduces to
respectively. Hence Equation (2) reduces to
 (3c)
(3c)
Using Equations (1), (2) and conditions (3a), (3b), (3c) we obtain the velocity profiles of various regions in the non-dimensional form as follows:
 (4)
(4)

Figure 2. Fluid flow in various regions in an annuli.
 (5)
(5)
 (6)
(6)
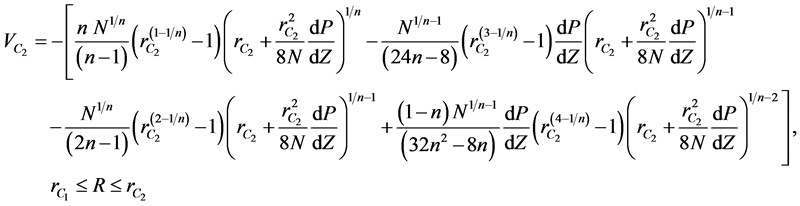 (7)
(7)
where the non-dimensional quantities are defined as follows:

The macroscopic mass and momentum balance equations are given by
 (8)
(8)
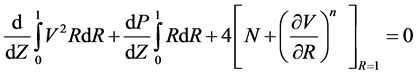 (9)
(9)
Using the velocity distribution in various regions and mass balance equation, one can find the variation of core in the entrance region for various parameter values. And the same has been computed numerically and reported elsewhere [9] .
Further, using velocity expressions in the Equations (8) and (9), the momentum balance equation in an algebraic form is given by
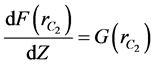 (10)
(10)
where
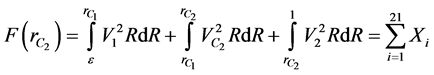 (11)
(11)
where  are given below
are given below
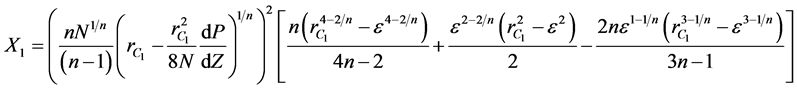
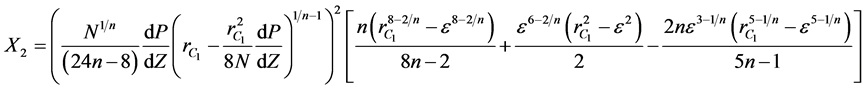

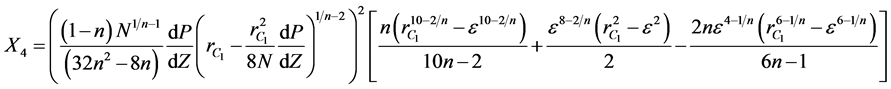

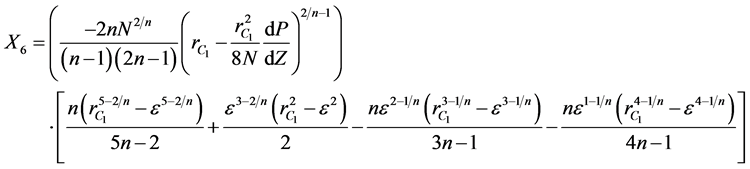
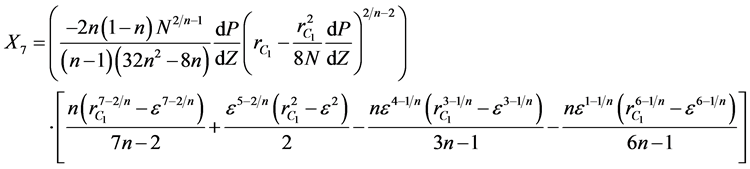
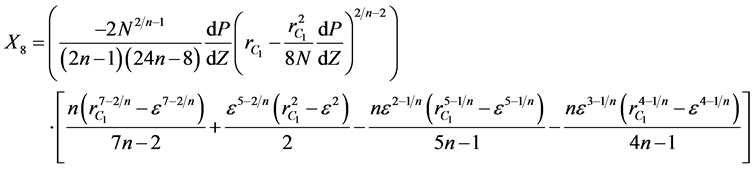
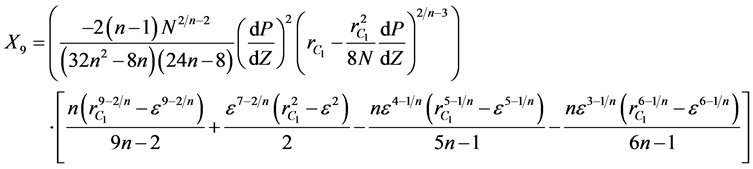
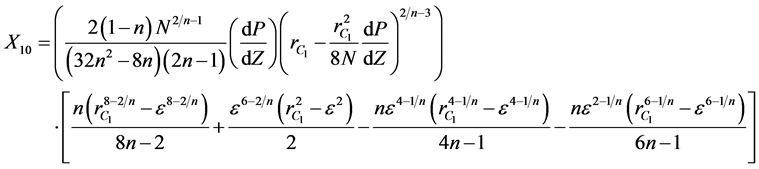
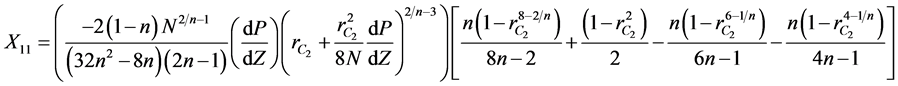


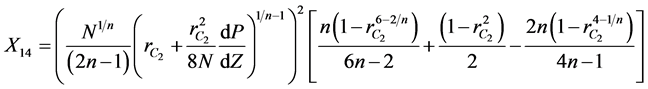
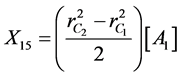
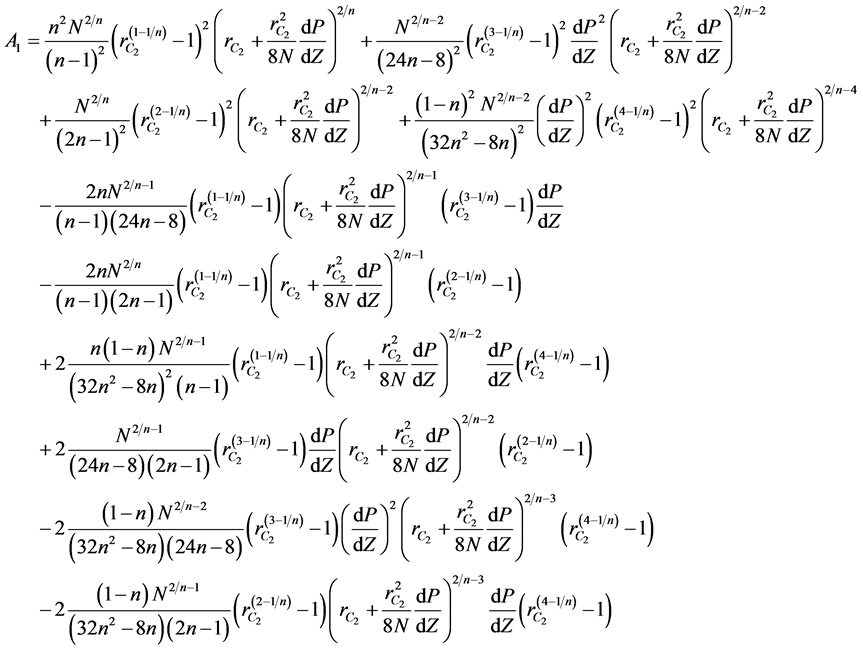

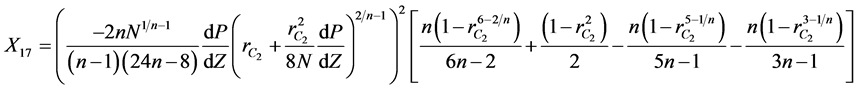
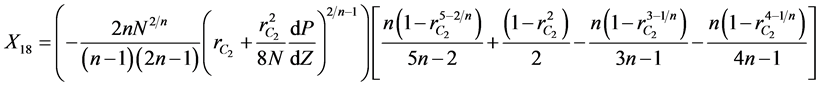
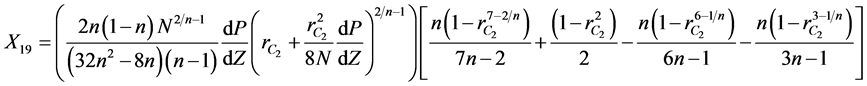

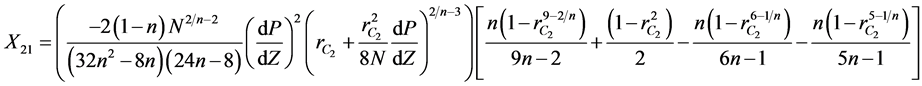
 (12)
(12)
Rewriting Equation (10) can be written as
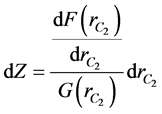 (13)
(13)
Integrating the above equation w.r.t. 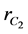 we get
we get
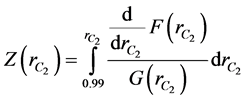 (14)
(14)
The solution of Equation (14) gives the relation between the core thickness and the dimensionless axial distance Z. Here,  is not defined. Hence, without making significant error, the lower limit of the integration of Equation (14) corresponding to the value
is not defined. Hence, without making significant error, the lower limit of the integration of Equation (14) corresponding to the value ![]() may be assumed to have the value
may be assumed to have the value 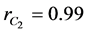 instead of 1, and the upper limit of the integration corresponds to the dimensionless core thickness
instead of 1, and the upper limit of the integration corresponds to the dimensionless core thickness . Equation (14) can be integrated numerically and the variation of entrance length along the dimensionless axial distance can be obtained for different values of Herschel-Bulkley number, flow behavior index and aspect ratios.
. Equation (14) can be integrated numerically and the variation of entrance length along the dimensionless axial distance can be obtained for different values of Herschel-Bulkley number, flow behavior index and aspect ratios.
Again, From Equation (8), we can say that the pressure gradient is a function of , i.e.
, i.e.  Thenusing the condition thatthe pressure is constant and equal to
Thenusing the condition thatthe pressure is constant and equal to  at the entrance, the pressure drop can be expressed as
at the entrance, the pressure drop can be expressed as
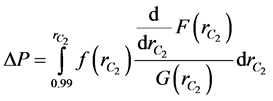 (15)
(15)
Again, the above equation can be numerically integrated for various values of Herschel-Bulkley number, flow behavior index and aspect ratios for the pressure drop.
3. Results and Discussion
The solution of the entrance region flow of a Herschel-Bulkley fluid through an annular cylinder has been investigated numerically without prior assumptions on the form of the velocity profile in the developing boundary layer. Initially, a nonlinear algebraic equation for determining the pressure gradient as a function of core thickness has been derived using the mass balance equation. This equation has been solved using an iterative procedure to obtain 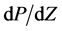 numerically. Using the values of pressure gradient so obtained, in the momentum balance equation, we obtain the entrance length for various values of Herschel-Bulkley number, flow behavior index and aspect ratios of the annuli. The entrance length has been defined as the distance at which 99 percent of fully developed velocity is reached.
numerically. Using the values of pressure gradient so obtained, in the momentum balance equation, we obtain the entrance length for various values of Herschel-Bulkley number, flow behavior index and aspect ratios of the annuli. The entrance length has been defined as the distance at which 99 percent of fully developed velocity is reached.
Figures 3-5 shows the variation of entrance length with core thickness when flow behavior index is n = 0.55 and Herschel-Bulkley number is 0.1, for various values of aspect ratio. It is observed that as aspect ratio increases, for particular Herschel-Bulkley number and flow behavior index, the entrance length decreases.
From Figure 3 and Figure 6 we can conclude that as the Herschel-Bulkley number increases for a given aspect ratio and flow behavior index entrance length decreases. Also, the similar results were observed in Figure 7 and Figure 8, when the flow behavior index is changed. This indicates that plug core will be very high for materials having thick viscosity, like mineral oils and polymer thickened fluid.
Further, from the results it is evident that as the value of flow behavior index “n” decreases, entrance length decreases for a fixed value of Herschel-Bulkley number and annuli aspect ratio.
It is observed that at any cross section Z, the entrance length decreases with the increase in aspect ratio of the annuli. Further, it is noted that as the Herschel-Bulkley number increases, the value of entrance length diminishes, that is, thick viscous fluids attains the fully developed state at early stage compared to that of Newtonian fluid like water.

Figure 3. The Variation of entrance length with core thickness for ε = 0.4, N = 0.1, n = 0.55.

Figure 4. The Variation of entrance length with core thickness for ε = 0.5, N = 0.1, n = 0.55.

Figure 5. The Variation of entrance length with core thickness for ε = 0.6, N = 0.1, n = 0.55.

Figure 6. The Variation of entrance length with core thickness for ε = 0.4, N = 0.15, n = 0.55.

Figure 7. The Variation of entrance length with core thickness for ε = 0.5, N = 0.15, n = 0.6.
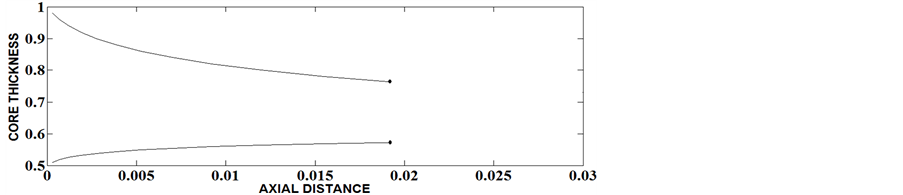
Figure 8. The Variation of core thickness along axial distance for ε = 0.5, N = 0.2, n = 0.6.
Expressing pressure gradient as a function of  and integrating from 0.99 to fully developed value, the pressure drop along the axial distance has been determined for different values of Herschel-Bulkley number, flow behavior index and aspect ratios and given as Figures 9-14. It is observed that at any cross section pressure drop is greater for materials with larger values of Herschel-Bulkley number for a particular aspect ratio. For a particular value of Herschel-Bulkley number and at a particular cross section, pressure drop decreases with the increase of aspect ratio. The velocity profile along the radial direction is shown in Figures 15-20. From these figures it is found that with the increase in Herschel-Bulkley number, the velocity decreases and its profile takes parabolic form for smaller values of Herschel-Bulkley number which can be approximated to that of Newtonian fluid. Further, velocity tends to decrease with the increase of aspect ratio.
and integrating from 0.99 to fully developed value, the pressure drop along the axial distance has been determined for different values of Herschel-Bulkley number, flow behavior index and aspect ratios and given as Figures 9-14. It is observed that at any cross section pressure drop is greater for materials with larger values of Herschel-Bulkley number for a particular aspect ratio. For a particular value of Herschel-Bulkley number and at a particular cross section, pressure drop decreases with the increase of aspect ratio. The velocity profile along the radial direction is shown in Figures 15-20. From these figures it is found that with the increase in Herschel-Bulkley number, the velocity decreases and its profile takes parabolic form for smaller values of Herschel-Bulkley number which can be approximated to that of Newtonian fluid. Further, velocity tends to decrease with the increase of aspect ratio.
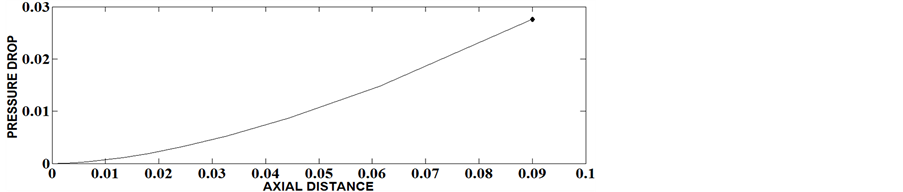
Figure 9. The Variation of pressure drop with the core thickness for ε = 0.4, N = 0.1, n = 0.55.
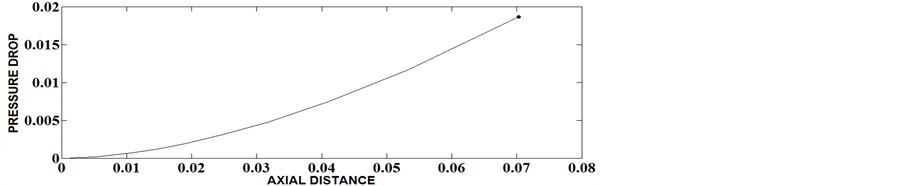
Figure 10. The Variation of pressure drop along axial distance for ε = 0.5, N = 0.1, n = 0.55.
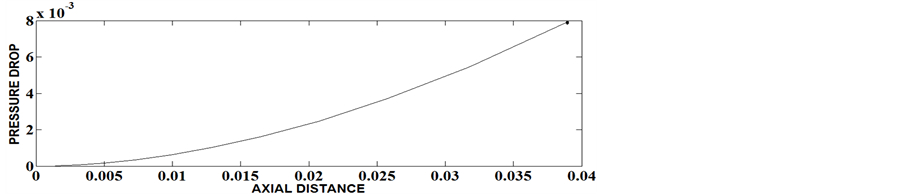
Figure 11. The Variation of pressure drop along axial distance for ε = 0.6, N = 0.1, n = 0.55.

Figure 12. The Variation of pressure drop with the core thickness for ε = 0.4, N = 0.15, n = 0.55.

Figure 13. The Variation of pressure drop along axial distance for ε = 0.5, N = 0.15, n = 0.6.

Figure 14. The Variation of pressure drop with the core thickness for ε = 0.5, N = 0.2, n = 0.6.

Figure 15. The velocity profile in the entrance region for ε = 0.4, N = 0.1, n = 0.55.

Figure 16. The velocity profile in the entrance region for ε = 0.5, N = 0.1, n = 0.55.
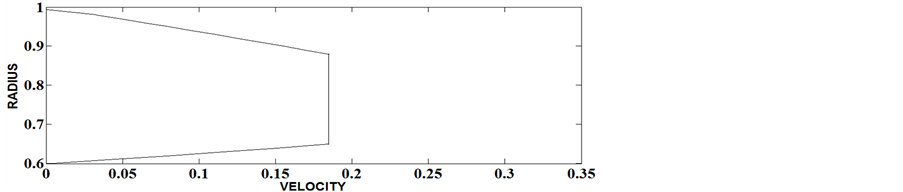
Figure 17. The velocity profile in the entrance region for ε = 0.6, N = 0.1, n = 0.55.

Figure 18. The velocity profile in the entrance region for ε = 0.4, N = 0.15, n = 0.55.

Figure 19. The velocity profile in the entrance region for ε = 0.5, N = 0.15, n = 0.6.
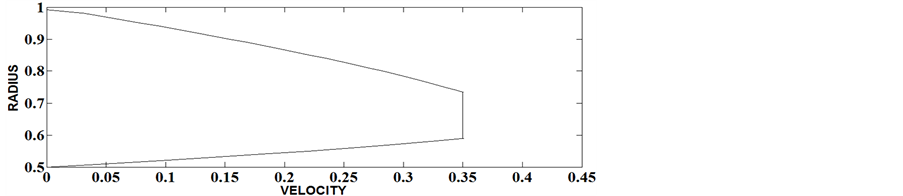
Figure 20. The velocity profile in the entrance region for ε = 0.5, N = 0.2, n = 0.6.
4. Conclusions
From the present study of the entrance region flow of Herschel-Bulkley fluid in an annuli, the following conclusion can be drawn:
1) The entrance length decreases when the width of annuli decreases for any particular Herschel-Bulkley fluid.
2) Thick viscous fluid attains fully developed state at early stage compared to that of Newtonian fluid.
3) At any cross section of the annuli, pressure drop is greater for materials with large values of HerschelBulkley number.
4) The velocity profile takes the parabolic form for smaller values of Herschel-Bulkley number which can be approximated to that of a Newtonian fluid.
Acknowledgements
The Authors thank the reviewers for their useful comments and suggestions.
References
- Batra, R.L. and Jena, B. (1990) Entrance Region Flow of Blood in Concentric Annulus. International Journal of Engineering Science, 28, 407-419. http://dx.doi.org/10.1016/0020-7225(90)90006-5
- Tandon, P.N., Srivastava, L.M. and Kushwaha, K. (1994) Developing Bloodflow in the Entrance Region of an Artery. International Journal of Bio-Medical Computing, 36, 257-265. http://dx.doi.org/10.1016/0020-7101(94)90079-5
- Dash, R.K., Jayaraman, G. and Mehta, K.N. (1996) Estimation of Increased Flow Resistance in a Narrow Catheterized Artery—A theoretical model. Journal of Biomechanics, 29, 917-930. http://dx.doi.org/10.1016/0021-9290(95)00153-0
- Gupta, R.C. (2001) On Developing Laminar Non-Newtonian Flow in Pipes and Channels. Nonlinear Analysis: Real World Applications, 2, 171-193. http://dx.doi.org/10.1016/S0362-546X(00)00109-7
- Maia, M.C.A. and Gasparetto, C.A. (2003) A Numerical Solution for the Entrance Region of Non-Newtonian Flow in Annuli. Brazilian Journal of Chemical Engineering, 20, 1-18. http://dx.doi.org/10.1590/S0104-66322003000200014
- Sankar, D.S. and Hemalatha, K. (2007) Pulsatile Flow of Herschel-Bulklely Fluid through Catherized Arteries—A Mathematical Model. Applied Mathematical Modeling, 31, 1497-1517. http://dx.doi.org/10.1016/j.apm.2006.04.012
- Poole, R.J. and Chhabra, R.P. (2010) Development Length Requirements for Fully Developed Laminar Pipe Flow of Yield Stress fluids. Journal of Fluids Engineering, 132, 034501-034504. http://dx.doi.org/10.1115/1.4001079
- Kandasamy, A. and Pai, R.G. (2013) Core Variation in the Entrance Region Flow of Casson Fluid in an Annuli. Applied Mechanics and Materials, 391, 376-381. http://dx.doi.org/10.4028/www.scientific.net/AMM.391.376
- Kandasamy, A. and Pai, R.G. (2014) Core Variation in the Entrance Region Flow of Herschel-Bulkley Fluid in an Annuli. Accepted for International Conference of Mechanical Engineering to Be Held at Imperial College London, July 2014.

