Applied Mathematics
Vol.5 No.10(2014), Article
ID:46523,7
pages
DOI:10.4236/am.2014.510142
Optimal Dividend Problem for a Compound Poisson Risk Model
Ying Shen, Chuancun Yin*
School of Mathematical Sciences, Qufu Normal University, Qufu, China
Email: *ccyin@mail.qfnu.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 April 2014; revised 3 May 2014; accepted 10 May 2014
ABSTRACT
In this note we study the optimal dividend problem for a company whose surplus process, in the absence of dividend payments, evolves as a generalized compound Poisson model in which the counting process is a generalized Poisson process. This model includes the classical risk model and the Pólya-Aeppli risk model as special cases. The objective is to find a dividend policy so as to maximize the expected discounted value of dividends which are paid to the shareholders until the company is ruined. We show that under some conditions the optimal dividend strategy is formed by a barrier strategy. Moreover, two conjectures are proposed.
Keywords:Barrier Strategy, Optimal Dividend Strategy, Generalized Compound Poisson Risk Model, Stochastic Control

1. Introduction
In recent decades, the optimization problem of dividend has received remarkable attention in the financial mathematics and insurance mathematics. This problem goes back to Finetti [1] , who considered a discrete time random walk with step size ±1 and found that the optimal dividend strategy is a barrier strategy, that is, any surplus above a certain level would be paid as dividend. Since then, many researchers have studied the dividends problems for various risk models under a barrier strategy. For the compound Poisson model, this problem was solved by Gerber [2] , identifying so-called band strategies as the optimal ones. For exponentially distributed claim sizes this strategy simplifies to a barrier strategy. Azcue and Nuler [3] follows a viscosity approach to investigate optimal reinsurance and dividend strategies in the Cramér-Lundberg model. Albrecher and Thonhauser [4] showed that the optimality of barrier strategies in the classical model with exponential claims still holds if there is a constant force of interest. Avram et al. [5] considered the case where the risk process is given by a general spectrally negative Lévy process and gave a sufficient condition involving the generator of the Lévy process for optimality of the barrier strategy. Loeffen [6] showed that barrier strategy is optimal among all admissible strategies for general spectrally negative Lévy risk processes with completely monotone jump density, and Kyprianou et al. [7] relaxed this condition on the jump density to log-convex. An alternative proof is given in Yin and Wang [8] . Loeffen and Renaud [9] pushed this result further by assuming the weaker condition that the Lévy measure has a density which is log-convex. Azcue and Muler [10] examine the analogous questions in the compound Poisson risk model with investment.
The Poisson processes are the most basic and widely used stochastic model for modeling discrete data, it may provide a poor fit in the presence of over-dispersion. For example, the use of the Poisson distribution as a model describing the number of claims caused by individual policyholders (e.g. in automobile insurance) during to that certain period is usually rejected, since in practice the behavior of policyholders is heterogeneous. In such a case the standard Poisson model is inappropriate. For example, in collective risk theory, it is assumed that claims occur in bulk, where the number of bulks  occurring in
occurring in 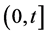 follows a Poisson process with parameter
follows a Poisson process with parameter . Each bulk consists of a random number of claims so that the total number of claims is of the form
. Each bulk consists of a random number of claims so that the total number of claims is of the form
 where
where 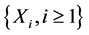 denotes the number of claims in the
denotes the number of claims in the 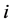 -th bulk. The aggregate claim payments made up to time
-th bulk. The aggregate claim payments made up to time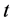 , called the generalized Poisson process, is given by
, called the generalized Poisson process, is given by 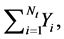 where
where 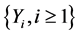
representing the individual claim amounts. In this paper, we formulate and solve an optimal dividends problem for a generalized Poisson risk model in which the aggregate claim payments are defined by a generalized Poisson process.
The rest of the paper is organized as follows. In Section 2, we give a rigorous mathematical formulation of the problem. Section 3 gives notion of log-convexity and complete monotonicity. We present our main results in Section 4 and prove them in Section 5.
2. Problem Setting
Consider the risk model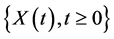 , defined on the filtered probability space
, defined on the filtered probability space 
and,
 (2.1)
(2.1)
where 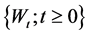 is a standard Brownian motion with
is a standard Brownian motion with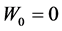 , the claim sizes
, the claim sizes 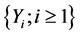 are positive independent and identically distributed random variables whose probability distribution function is given by
are positive independent and identically distributed random variables whose probability distribution function is given by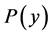 ,
,
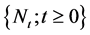 is a generalized Poisson process defined as
is a generalized Poisson process defined as  where
where 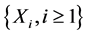 are discrete independent and identically distributed random variables whose probability distribution is given by
are discrete independent and identically distributed random variables whose probability distribution is given by
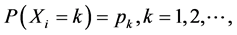 and
and 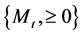 is a homogeneous Poisson process with intensity
is a homogeneous Poisson process with intensity .
.
Moreover, it is assumed that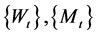 ,
,  and
and 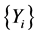 are mutually independent. In particular, when
are mutually independent. In particular, when
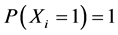 , the process
, the process 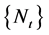 reduces to the homogeneous Poisson process with intensity
reduces to the homogeneous Poisson process with intensity , and hence the risk model (2.1) reduces to the classical risk model perturbed by Brownian motion (see Chiu and Yin [11] ).
, and hence the risk model (2.1) reduces to the classical risk model perturbed by Brownian motion (see Chiu and Yin [11] ).
The probability mass function of 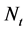 is given by
is given by
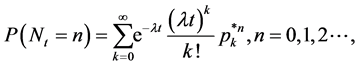 (2.2)
(2.2)
where 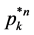 is the
is the 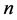 -fold convolution of
-fold convolution of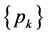 . In a few special cases it is possible to determine the probabilities
. In a few special cases it is possible to determine the probabilities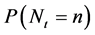 ’s explicitly.
’s explicitly.
Example 2.1. Suppose that 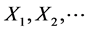 are geometrically distributed with parameter
are geometrically distributed with parameter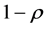 , where
, where , i.e.
, i.e.
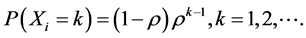
Then the compound Poisson process by geometric compounding leads to the Pólya-Aeppli process
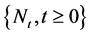 with parameters
with parameters 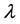 and
and 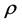 (cf. Minkova [12] ). That is for all
(cf. Minkova [12] ). That is for all ,
,
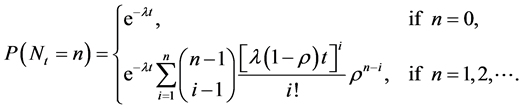 (2.3)
(2.3)
Note that the Pólya-Aeppli process is a time-homogeneous process, it is also called Poisson-geometric process in Chinese literature, for example see Mao and Liu [13] , where the ruin probability was studied for compound Poisson-geometric process. In the case of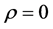 , the Pólya-Aeppli process becomes a homogeneous Poisson process.
, the Pólya-Aeppli process becomes a homogeneous Poisson process.
Example 2.2. (Quenouille [14] ) Let 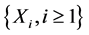 denote a sequence of independent and identically distributed random variables, each one having the logarithmic distribution (also known as the logarithmic series distribution)
denote a sequence of independent and identically distributed random variables, each one having the logarithmic distribution (also known as the logarithmic series distribution) , with probability mass function
, with probability mass function
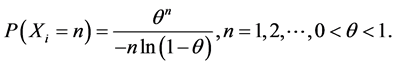
Suppose that  has a Poisson process with parameter
has a Poisson process with parameter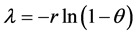 . Then the random sum
. Then the random sum
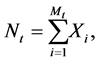
has the negative binomial distribution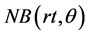 :
:
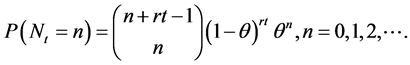 (2.4)
(2.4)
In this way, the negative binomial distribution is seen to be a compound Poisson distribution.
We now consider the classical optimal dividend control problem. Let  be a dividend strategy consisting of a non-decreasing left-continuous
be a dividend strategy consisting of a non-decreasing left-continuous 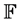 -adapted process
-adapted process 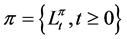 with
with , where
, where  represents the cumulative dividends paid out by the company till time
represents the cumulative dividends paid out by the company till time  under the control
under the control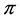 . We define the controlled risk process
. We define the controlled risk process  by
by . Let
. Let 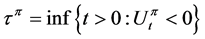 be the ruin time and define the value function of a dividend strategy
be the ruin time and define the value function of a dividend strategy 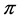 by
by
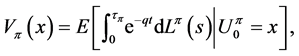
where 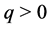 is an interest force for the calculation of the present value. Let
is an interest force for the calculation of the present value. Let 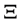 be the set of all admissible dividend strategies, that is all strategies
be the set of all admissible dividend strategies, that is all strategies 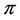 such that
such that 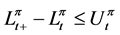 for
for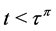 . The objective is to solve the following stochastic control problem:
. The objective is to solve the following stochastic control problem:
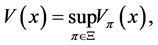 (2.5)
(2.5)
and to find an optimal policy 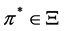 that satisfies
that satisfies 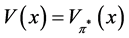 for all
for all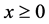 .
.
3. Log-Convexity and Complete Monotonicity
Before starting our main results, we introduce the definitions of log-convexity and complete monotonicity.
Definition 3.1. (Willmot and Lin [15] ). (1) A distribution 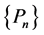 on the non-negative integers is said to be log-convex if
on the non-negative integers is said to be log-convex if 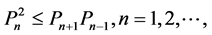 and
and 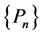 is said to be strictly log-convex if
is said to be strictly log-convex if 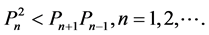
A counting distribution 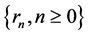 is discrete completely monotone iff it is a mixture of geometric distributions, i.e.
is discrete completely monotone iff it is a mixture of geometric distributions, i.e.
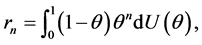
where  is a probability distribution on
is a probability distribution on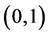 .
.
(2) A function 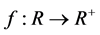 is log-convex if
is log-convex if 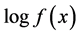 is a convex function. Let
is a convex function. Let  with
with
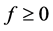 . We say
. We say 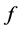 is completely monotone if
is completely monotone if 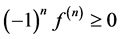 for all
for all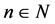 .
.
(3) The distribution function 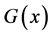 is said to be decreasing (increasing) failure rate or DFR (IFR) if
is said to be decreasing (increasing) failure rate or DFR (IFR) if
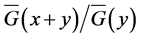 is nondecreasing (nonincreasing) in
is nondecreasing (nonincreasing) in  for fixed
for fixed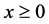 , i.e. if
, i.e. if  is log-convex
is log-convex
(log-concave).
Note that the completely monotone class is a subclass of the log-convex. For examples of continuous log-convex or completely monotone functions can be found in Yin and Wang [8] . Now, we give a discrete example.
Example 3.1. Let  be a logarithmic random variable with
be a logarithmic random variable with
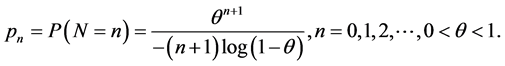
Then 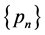 is completely monotone (see Van Harn ([16] , p. 58)). The generalized logarithmic series distribution is defined by
is completely monotone (see Van Harn ([16] , p. 58)). The generalized logarithmic series distribution is defined by
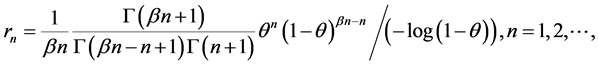
with 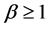 and
and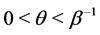 . Then
. Then 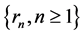 is strictly log-convex (see Hansen and Willekens [17] ).
is strictly log-convex (see Hansen and Willekens [17] ).
4. Main Results
Denote by  the constant barrier strategy at level
the constant barrier strategy at level 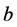 which is defined by
which is defined by 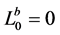 and
and

for all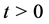 . That is, for a level
. That is, for a level 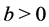 whenever surplus goes above
whenever surplus goes above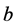 , the excess is paid as dividends to the shareholders of the company and, if the surplus is less than
, the excess is paid as dividends to the shareholders of the company and, if the surplus is less than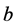 , no dividends are paid out. We will now present the main results of this note which give sufficient conditions for optimality of a barrier strategy
, no dividends are paid out. We will now present the main results of this note which give sufficient conditions for optimality of a barrier strategy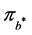 . It is important to note that various dividend strategies can be employed by an insurance company. However, we will only focus on the conditions for the optimality of a dividend strategy.
. It is important to note that various dividend strategies can be employed by an insurance company. However, we will only focus on the conditions for the optimality of a dividend strategy.
After some tedious calculations, we get

where
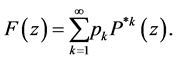 (4.1)
(4.1)
Here 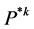 is the
is the 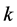 -fold convolution of
-fold convolution of 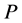 with itself. So that
with itself. So that 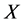 is a special spectrally negative Lévy process with the Laplace exponent
is a special spectrally negative Lévy process with the Laplace exponent . Therefore, all the known results for spectrally negative Lévy process models can be applied to the model (2.1). However, since the distribution function
. Therefore, all the known results for spectrally negative Lévy process models can be applied to the model (2.1). However, since the distribution function 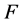 is not explicit (depends on the distribution of
is not explicit (depends on the distribution of  and
and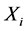 ), it can be of interest to study which assumptions on the probability distributions of
), it can be of interest to study which assumptions on the probability distributions of 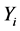 and
and 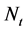 ensure that the optimal dividend strategy is barrier one.
ensure that the optimal dividend strategy is barrier one.
We now recall the definition of the 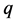 -scale function
-scale function  and some properties of this function. For each
and some properties of this function. For each 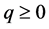 there exists a continuous and increasing function
there exists a continuous and increasing function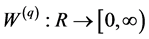 , called the
, called the 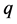 -scale function defined in such a way that
-scale function defined in such a way that 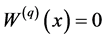 for all
for all 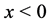 and on
and on 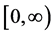 its Laplace transform is given by
its Laplace transform is given by

Here, 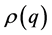 is the unique root of equation
is the unique root of equation  in the half-plane
in the half-plane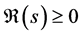 .
.
From Avram et al. [5] we get the expected discounted value of dividend payments of the barrier strategy at level  is given by
is given by
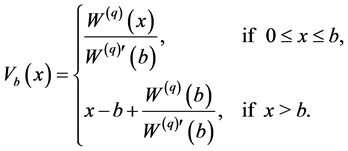 (4.2)
(4.2)
Define
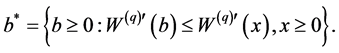
Theorem 4.1. For model (2.1), if 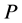 has a completely monotone probability density function on
has a completely monotone probability density function on 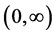 and
and
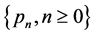 is discrete completely monotone, then the barrier strategy with level
is discrete completely monotone, then the barrier strategy with level 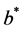 is the optimal dividend strategy. Moreover, the
is the optimal dividend strategy. Moreover, the 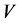 defined by (2.5) is given by
defined by (2.5) is given by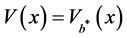 .
.
Theorem 4.2. For model (2.1), if  is discrete completely monotone and
is discrete completely monotone and 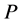 is DFR, then the barrier strategy with level
is DFR, then the barrier strategy with level  is the optimal dividend strategy. Moreover, the
is the optimal dividend strategy. Moreover, the 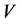 defined by (2.5) is given by
defined by (2.5) is given by
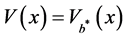 .
.
Corollary 4.1. For model (2.1) with 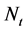 given by (2.3) or (2.4), if
given by (2.3) or (2.4), if  is DFR, then the barrier strategy with level
is DFR, then the barrier strategy with level 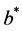 is the optimal dividend strategy. Moreover, the
is the optimal dividend strategy. Moreover, the 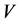 defined by (2.5) is given by
defined by (2.5) is given by .
.
Theorem 4.3. For model (2.1), if 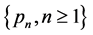 is a log-convex probability mass function and
is a log-convex probability mass function and 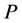 is the exponential distribution function with mean
is the exponential distribution function with mean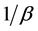 , then the barrier strategy with level
, then the barrier strategy with level 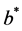 is the optimal dividend strategy. Moreover, the
is the optimal dividend strategy. Moreover, the  defined by (2.5) is given by
defined by (2.5) is given by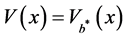 .
.
5. Proof of Main Results
Before proving the main results, we give several lemmas.
Lemma 5.1. (Loeffen [13] ) Suppose that the Lévy measure of a spectrally negative Lévy process  has a completely monotone density on
has a completely monotone density on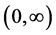 , then the barrier strategy at
, then the barrier strategy at  is an optimal strategy.
is an optimal strategy.
Kyprianou, Rivero and Song [7] providing weaker conditions on the Lévy measure for the optimality of a barrier strategy. An alternative approach can be found in Yin and Wang [8] .
Lemma 5.2. Suppose that a spectrally negative Lévy process 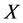 has a Lévy density
has a Lévy density 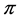 on
on 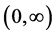 that is log-convex, then the barrier strategy at
that is log-convex, then the barrier strategy at 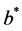 is an optimal strategy.
is an optimal strategy.
Note that for the Cramér-Lundberg model with or without a Brownian component, the requirement of log-convexity of the Lévy density 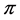 on
on  is equivalent to the log-convexity of the probability density function of the individual claim amount on
is equivalent to the log-convexity of the probability density function of the individual claim amount on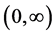 . Since the Lévy measure having a log-convex (or completely monotone) density implies that tail of the Lévy measure is log-convex and the converse is not true (cf. Loeffen and Renaud [9] ), the following result improves the results in Lemmas 3.1 and 3.2.
. Since the Lévy measure having a log-convex (or completely monotone) density implies that tail of the Lévy measure is log-convex and the converse is not true (cf. Loeffen and Renaud [9] ), the following result improves the results in Lemmas 3.1 and 3.2.
Lemma 5.3. (Loeffen and Renaud [9] ) Suppose that the tail of the Lévy measure of a spectrally negative Lévy process 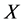 is log-convex, then the barrier strategy at
is log-convex, then the barrier strategy at 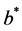 is an optimal strategy.
is an optimal strategy.
Proof of Theorem 4.1. If 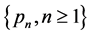 is discrete completely monotone and
is discrete completely monotone and 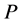 has a completely monotone density on
has a completely monotone density on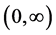 , then
, then
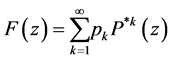
has a completely monotone density on  (cf. Chiu and Yin [18] ). The result follows from Lemma 5.1.
(cf. Chiu and Yin [18] ). The result follows from Lemma 5.1.
Proof of Theorem 4.2. It is well known that the property of DFR is preserved under the geometric sum (see Shanthikumar [19] , Corollary (3.6)), and since the sum of two log-convex functions is log-convex and the limit of a pointwise convergent sequence of log-convex functions is log-convex, it follows that
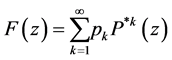
is also DFR. The result of Theorem 4.2 follows from Lemma 5.3.
Proof of Theorem 4.3. If 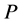 is the exponential distribution function with mean
is the exponential distribution function with mean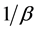 , then by (4.1) we have
, then by (4.1) we have
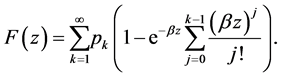
Therefore,

Interchanging the order of summation yields

where
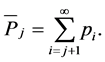
Note that 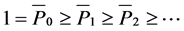 and
and  is increasing in
is increasing in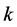 , it follows from Theorem 3.2 in Esary and Marshall [20] that
, it follows from Theorem 3.2 in Esary and Marshall [20] that  has a density which is logarithmically convex on
has a density which is logarithmically convex on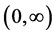 . The result follows from Lemmas 5.2.
. The result follows from Lemmas 5.2.
Remark 5.1. At the end of this paper, we give two conjectures. The first conjecture can be viewed as an extension of Theorem 4.3; The second conjecture can be viewed as an extension of Conjecture 1 and Theorem 4.2.
Conjecture 1. For model (2.1), if  is a log-convex and
is a log-convex and 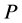 has a density
has a density 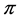 on
on 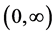 that is log-convex, then the barrier strategy at
that is log-convex, then the barrier strategy at 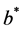 is an optimal strategy for stochastic control problem (2.5).
is an optimal strategy for stochastic control problem (2.5).
Conjecture 2. For model (2.1), if 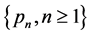 is DFR and
is DFR and 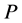 is DFR, then the barrier strategy at
is DFR, then the barrier strategy at  is an optimal strategy for stochastic control problem (2.5).
is an optimal strategy for stochastic control problem (2.5).
Acknowledgements
We would like to thank the anonymous referee who gave us many constructive suggestions and valuable comments on the previous version of this paper. The research was supported by the National Natural Science Foundation of China (No. 11171179), the Research Fund for the Doctoral Program of Higher Education of China (No. 20133705110002) and the Program for Scientific Research Innovation Team in Colleges and Universities of Shandong Province.
References
- Finetti, B.D. (1957) Su un’impostazion alternativa dell teoria collecttiva del rischio. Transactions of the 15th International Congress of Actuaries, 2, 433-443.
- Gerber, H.U. (1969) Entscheidungskriterien für den zusammengesetzten Poisson-Prozess. Mitteilungen der Vereinigung Schweizerischer Versicherungsmathematiker, 69, 185-227.
- Azcue, P. and Muler, N. (2005) Optimal Reinsurance and Dividend Distribution Policies in the Cramér-Lundberg Model. Mathematical Finance, 15, 261-308. http://dx.doi.org/10.1111/j.0960-1627.2005.00220.x
- Albrecher, H. and Thonhauser, S. (2008) Optimal Dividend Strategies for a Risk Process under Force of Interest. Insurance: Mathematics and Economics, 43, 134-149. http://dx.doi.org/10.1016/j.insmatheco.2008.03.012
- Avram, F. Palmowski, Z. and Pistorius, M.R. (2007) On the Optimal Dividend Problem for a Spectrally Negative Lévy Process. The Annals of Applied Probability, 17, 156-180. http://dx.doi.org/10.1214/105051606000000709
- Loeffen, R. (2008) On Optimality of the Barrier Strategy in de Finetti’s Dividend Problem for Spectrally Negative Lévy Processes. The Annals of Applied Probability, 18, 1669-1680. http://dx.doi.org/10.1214/07-AAP504
- Kyprianou, A.E. Rivero, V. and Song, R. (2010) Convexity and Smoothness of Scale Functions with Applications to de Finetti’s Control Problem. Journal of Theoretical Probability, 23, 547-564. http://dx.doi.org/10.1007/s10959-009-0220-z
- Yin, C.C. and Wang, C.W. (2009) Optimality of the Barrier Strategy in de Finetti’s Dividend Problem for Spectrally Negative Lévy Processes: An Alternative Approach. Journal of Computational and Applied Mathematics, 233, 482- 491. http://dx.doi.org/10.1016/j.cam.2009.07.051
- Loeffen, R. and Renaud, J.F. (2010) De Finetti’s Optimal Dividends Problem with an Affine Penalty Function at Ruin. Insurance: Mathematics and Economics, 46, 98-108. http://dx.doi.org/10.1016/j.insmatheco.2009.09.006
- Azcue, P. and Muler, N. (2010) Optimal Investment Policy and Dividend Payment Strategy in an Insurance Company. The Annals of Applied Probability, 20, 1253-1302. http://dx.doi.org/10.1214/09-AAP643
- Chiu, S.N. and Yin, C.C. (2003) The Time of Ruin the Surplus Prior to Ruin and the Deficit at Ruin for the Classical Risk Process Perturbed by Diffusion. Insurance: Mathematics and Economics, 33, 59-66. http://dx.doi.org/10.1016/S0167-6687(03)00143-4
- Minkova, L.D. (2004) The Pólya-Aeppli Process and Ruin Problems. Journal of Applied Mathematics and Stochastic Analysis, 3, 221-234. http://dx.doi.org/10.1155/S1048953304309032
- Mao, Z.C. and Liu, J.E. (2005) A Risk Model and Ruin Probability with Compound Poisson-Geometric Process. Acta Mathematicae Applicatae Sinica, 28, 419-428. (in Chinese)
- Quenouille, M.H. (1949) A Relation between the Logarithmic, Poisson, and Negative Binomial Series. Biometrics, 5, 162-164. http://dx.doi.org/10.2307/3001917
- Willmot, G.E. and Lin, X.S. (2001) Lundberg Approximations for Compound Distributions with Insurance Applications. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4613-0111-0
- Van Harn, K. (1978) Classifying Infinitely Divisible Distributions by Functional Equations. CWI, Amsterdam.
- Hansen, B.G. and Willekens, E. (1990) The Generalized Logarithmic Series Distribution. Statistics & Probability Letters, 9, 311-316. http://dx.doi.org/10.1016/0167-7152(90)90138-W
- Chiu, S.N. and Yin, C.C. (2014) On the Complete Monotonicity of the Compound Geometric Convolution with Applications to Risk Theory. Scandinavian Actuarial Journal, 2014, 116-124. http://dx.doi.org/10.1080/03461238.2011.647061
- Shanthikumar, J.G. (1988) DFR Property of First Passage Times and Its Preservation under Geometric Compounding. The Annals of Probability, 16, 397-406. http://dx.doi.org/10.1214/aop/1176991910
NOTES

*Corresponding author.

