Applied Mathematics
Vol.5 No.8(2014), Article ID:45702,3 pages DOI:10.4236/am.2014.58114
A Simple Way to Prove the Characterization of Differentiable Quasiconvex Functions
Giorgio Giorgi
Faculty of Economics, University of Pavia, Pavia, Italy
Email: ggiorgi@eco.unipv.it
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 23 January 2014; revised 23 February 2014; accepted 2 March 2014
ABSTRACT
We give a short and easy proof of the characterization of differentiable quasiconvex functions.
Keywords:Quasiconvex Functions, Generalized Convexity

1. Introduction
Quasiconvex functions play an important role in several branches of applied mathematics (e.g. mathematical programming, minimax theory, games theory, etc.) and of economic analysis (production theory, utility theory, etc.). De Finetti [1] was one of the first mathematicians to define quasiconvex functions as those functions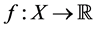 ,
, 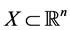 being a convex set, having convex lower level sets, i.e. the set
being a convex set, having convex lower level sets, i.e. the set

is convex for every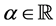 .
.
De Finetti did not name this class of functions: the term “quasiconvex (quasiconcave) function” was given subsequently by Fenchel [2] . It is well-known that the above characterization is equivalent to
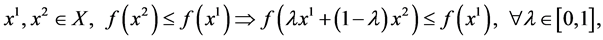
i.e., in a more symmetric way,
When f is differentiable on the open convex set  we have the following characterization of a quasiconvex function.
we have the following characterization of a quasiconvex function.
Theorem 1. Let  be differentiable on the open convex set
be differentiable on the open convex set  Then f is quasiconvex on X if and only if
Then f is quasiconvex on X if and only if
 (1)
(1)
Theorem 1 was given by Arrow and Enthoven [3] ; however, these authors prove, in a short and easy way, only the necessary part of the theorem, but not the converse property, whose proof is indeed presented in a quite intricate way by several authors (see, e.g. [4] -[11] ). Here we present an easy proof of Theorem 1, by exploiting some results on quasiconvexity of functions of one variable, results therefore suitable for geometrical illustrations. We need two lemmas.
Lemma 1. Let ,
,  a convex set. Then f is quasiconvex on X if and only if the restriction of f on each line segment contained in X is a quasiconvex function, i.e. if and only if the function
a convex set. Then f is quasiconvex on X if and only if the restriction of f on each line segment contained in X is a quasiconvex function, i.e. if and only if the function 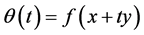 is quasiconvex on the interval
is quasiconvex on the interval
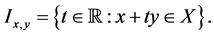
Proof. The quasiconvexity of 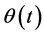 is equivalent to the implication
is equivalent to the implication

By setting 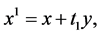
 we have
we have 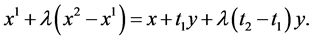 The thesis follows by noting that
The thesis follows by noting that 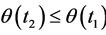 and the logical implication
and the logical implication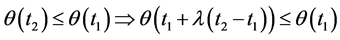 ,
, 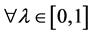 are equivalent to
are equivalent to  and
and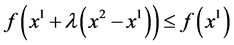 ,
, 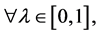 respectively.
respectively. 
The next lemma is proved in Cambini and Martein [12] and is given also by Crouzeix [13] , without proof.
Lemma 2. Let  be differentiable on the interval
be differentiable on the interval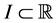 ; then
; then  is quasiconvex on I if and only if
is quasiconvex on I if and only if
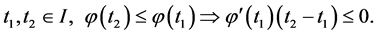 (2)
(2)
Proof. Let  such that
such that 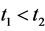
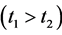 and
and 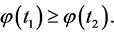 The quasiconvexity of
The quasiconvexity of  implies
implies 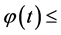
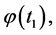

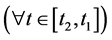 so that
so that 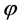 is locally non-increasing (locally non-decreasing) at t1 and consequently (2) holds. Assume now that (2) holds. If
is locally non-increasing (locally non-decreasing) at t1 and consequently (2) holds. Assume now that (2) holds. If 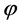 is not quasiconvex, there exist
is not quasiconvex, there exist 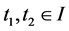 with
with 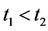
such that 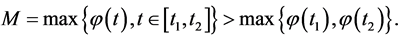 Let
Let 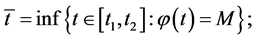 the continuity of
the continuity of
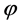 implies the existence of
implies the existence of 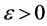 such that
such that 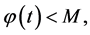
 and
and 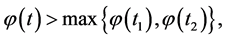
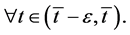 The mean value theorem applied to the interval
The mean value theorem applied to the interval 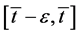 implies the existence of
implies the existence of
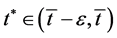 such that
such that  Consequently, we have
Consequently, we have 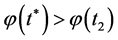 with
with 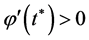 and this contradicts (2).
and this contradicts (2). 
Proof of Theorem 1.
It is sufficient to note that if 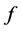 is differentiable on the open and convex set
is differentiable on the open and convex set  then we have, with
then we have, with 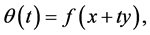
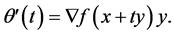
Therefore, on the ground of Lemmas 1 and 2, if we put 
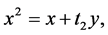 we have
we have 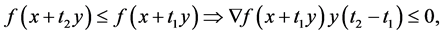 i.e.
i.e. 


Finally, we point out that the proof of Ponstein [10] can be shortened as follows:
1) Let 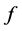 be quasiconvex (and differentiable) on the open and convex set
be quasiconvex (and differentiable) on the open and convex set 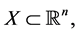 i.e. let
i.e. let
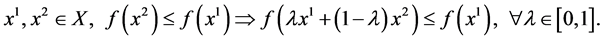
By the mean value theorem there exists a number  such that
such that
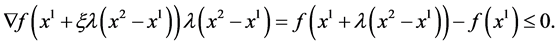
Dividing by  and letting
and letting  we have
we have 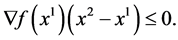
2) Assume conversely that (1) holds and that for 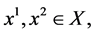 with
with  there exists a point
there exists a point 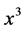 between
between 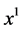 and
and 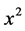 with
with 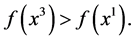 Then there exists near
Then there exists near 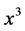 (e.g. between
(e.g. between 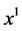 and
and ) also a point
) also a point 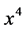 with
with 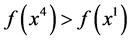 and
and 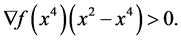 Indeed, if for all x between
Indeed, if for all x between 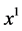 and
and 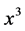 it would hold
it would hold 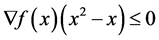 or
or 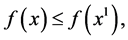 then we would have
then we would have 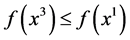 but not
but not 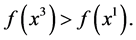 But, being
But, being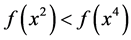 , this implies
, this implies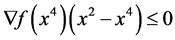 , in contradiction with the inequality previously obtained.
, in contradiction with the inequality previously obtained. 
References
- De Finetti, B. (1949) Sulle Stratificazioni Convesse. Annali di Matematica Pura ed Applicata, 30, 173-183. http://dx.doi.org/10.1007/BF02415006
- Fenchel, W. (1953) Convex Cones, Sets and Functions. Lecture Notes, Princeton University, Princeton.
- Arrow, K.J. and Enthoven, A.C. (1961) Quasi-Concave Programming. Econometrica, 29, 779-800. http://dx.doi.org/10.2307/1911819
- Avriel, M. (1976) Nonlinear Programming: Analysis and Methods. Prentice-Hall, Englewood Cliffs.
- Avriel, M., Diewert, W.E., Schaible, S. and Zang, I. (1988) Generalized Concavity. Plenum Press, New York. http://dx.doi.org/10.1007/978-1-4684-7600-2
- Bazaraa, M.S. and Shetty, C.M. (1976) Foundations of Optimization. Springer Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-48294-6
- Bazaraa, M.S., Sherali, H.D. and Shetty, C.M. (1993) Nonlinear Programming. John Wiley & Sons, New York.
- Kemp, M.C. and Kimura, Y. (1978) Introduction to Mathematical Economics. Springer Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-6278-7
- Mangasarian, O.L. (1969) Nonlinear Programming. McGraw-Hill, New York.
- Ponstein, J. (1967) Seven Kinds of Convexity. SIAM Review, 9, 115-119. http://dx.doi.org/10.1137/1009007
- Simon, C.P. and Blume, L. (1994) Mathematics for Economists. W. W. Norton & Co., New York.
- Cambini, A. and Martein, L. (2009) Generalized Convexity and Optimization. Springer, Berlin.
- Crouzeix, J.-P. (2005) Criteria for Generalized Convexity and Generalized Monotonicity in the Differentiable Case. In: Hadjisavvas, N., Komlosi, S. and Schaible, S., Eds., Handbook of Generalized Convexity and Generalized Monotonicity, Springer, New York, 89-119. http://dx.doi.org/10.1007/0-387-23393-8_2

