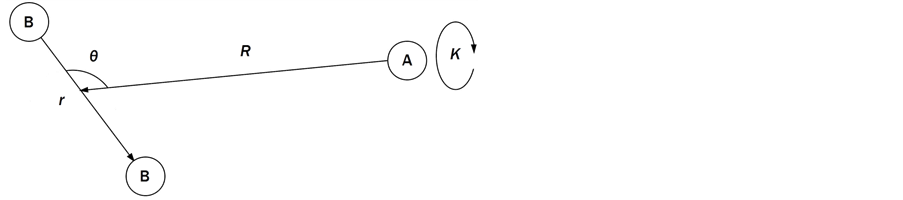Applied Mathematics
Vol.05 No.17(2014), Article ID:50606,7 pages
10.4236/am.2014.517263
Using ScalIT for Performing Accurate Rovibrational Spectroscopy Calculations for Triatomic Molecules: A Practical Guide
Corey Petty, Bill Poirier
Department of Chemistry and Biochemistry, Texas Tech University, Lubbock, Texas, USA
Email: bill.poirier@ttu.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 August 2014; 16 September 2014; accepted 21 September 2014
ABSTRACT
This paper presents a practical guide for use of the ScalIT software package to perform highly accurate bound rovibrational spectroscopy calculations for triatomic molecules. At its core, ScalIT serves as a massively scalable iterative sparse matrix solver, while assisting modules serve to create rovibrational Hamiltonian matrices, and analyze computed energy levels (eigenvalues) and wavefunctions (eigenvectors). Some of the methods incorporated into the package include: phase space optimized discrete variable representation, preconditioned inexact spectral transform, and optimal separable basis preconditioning. ScalIT has previously been implemented successfully for a wide range of chemical applications, allowing even the most state-of-the-art calculations to be computed with relative ease, across a large number of computational cores, in a short amount of time.
Keywords:
Rovibrational Spectroscopy, Iterative Matrix Solver, Lanczos, Quasiminimal Residual, Molecular Bound States, HO2

1. Introduction
ScalIT, in principle, can be applied across a broad range of scientific disciplines; however, recent development and application has been geared toward molecular chemical dynamics, performing exact time-independent quantum dynamics calculations. More specifically, it has been applied to compute bound rovibrational energy levels and wavefunctions. The software suite has been designed at the lowest level to scale across a large number of CPUs, and be as general as possible, allowing the scientific community to “tap” into ScalIT for use with their own algorithms. In this paper we focus on the operation of ScalIT from the non-expert user’s perspective, after a brief description of the underlying numerical methods. If a more detailed analysis is desired, the reader is referred to the literature [1] -[20] . High level modules have been created for performing calculations on systems up to four atoms; for simplicity, we restrict ourselves to discuss only triatomic molecules, although the procedure described is nearly identical for more difficult systems.
2. The “A Matrix” Form, and ScalIT Methodology
We present a broad overview of ScalIT’s core functionality here. The emphasis is to provide the reader with an understanding of where in the science landscape ScalIT lives, as well as how its iterative nature has fueled its success. In order to understand the process of using ScalIT, one must have a basic grasp of its problem scope, as well as the fundamental “nuts and bolts” of the machinery used.
We are solving the time independent Schrödinger equation (TISE) formulated for rovibrational dynamics of molecular systems, which is a symmetric eigenvalue/eigenvector problem. It is solved in a variational way, in which the rovibrational Hamiltonian is represented as a matrix, H, in a “basis” of grid points (we use a discrete variable representation (DVR)) distributed over position space. For a molecule of n atoms, there are 3n − 5 rovibrational degrees of freedom (dofs) that must explicitly be considered, which ScalIT describes using Jacobi coordinates. Therefore, triatomics have 4 dofs (r, R, θ, K), r being the distance between two atoms, typically taken to be the heavier two. R is the distance between the center of mass of r and the third atom, and θ the angle between r and R. K is a dof associated with rotation. Figure 1 shows a model of an AB2 triatomic molecule, meaning two of the atoms are of the same type.
A new Hamiltonian matrix is created and solved for each combination of the symmetry parameters J and ϵ, where J is the total angular momentum, and ϵ is inversion parity. With the coordinate system established, the triatomic Hamiltonian can be expressed as:
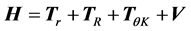 , (1)
, (1)
where  is the potential energy matrix, and
is the potential energy matrix, and 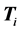 is the ith kinetic energy matrix associated with the ith dof.
is the ith kinetic energy matrix associated with the ith dof.  is a diagonal matrix, and each
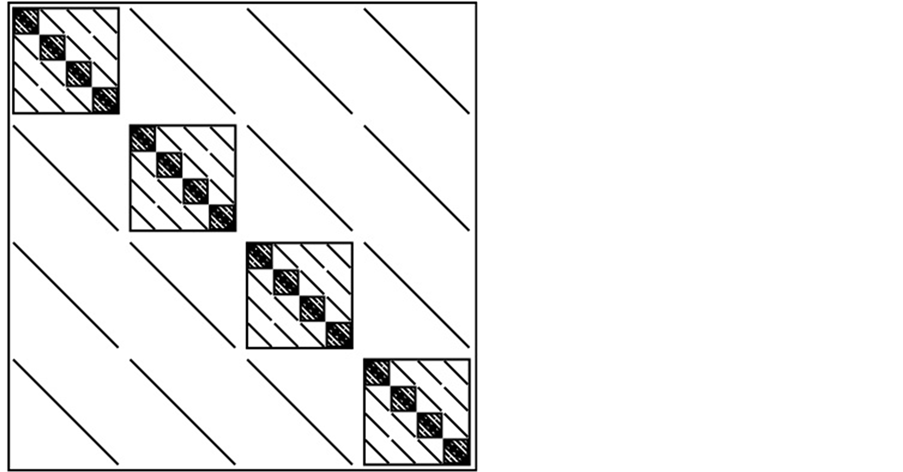
is a diagonal matrix, and each 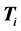 is diagonal with respect to all dofs excluding that of its own subscript(s). This discretized grid-based representation of the molecular Hamiltonian yields a resultant matrix with a highly structured block-form, characterized by diagonal blocks of precisely the same size, and off-diagonal blocks which are themselves diagonal. We term this the “
is diagonal with respect to all dofs excluding that of its own subscript(s). This discretized grid-based representation of the molecular Hamiltonian yields a resultant matrix with a highly structured block-form, characterized by diagonal blocks of precisely the same size, and off-diagonal blocks which are themselves diagonal. We term this the “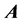 matrix form.” The
matrix form.” The 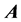 matrix is sparse, meaning that a large number of the matrix elements are zero. As the number of dofs increases, a fractal, self-similar pattern is produced which increases sparsity, while maintaining the same structure at all scales. A pictorial representation can be seen in Figure 2.
matrix is sparse, meaning that a large number of the matrix elements are zero. As the number of dofs increases, a fractal, self-similar pattern is produced which increases sparsity, while maintaining the same structure at all scales. A pictorial representation can be seen in Figure 2.
Sparsity of the 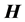 matrix is an important numerical consideration, given that the matrix dimensionality, N, scales exponentially with the number of dofs. Consequently, direct diagonalization routines such as Householder’s algorithm, for which memory requirements scale as N2, and computational effort as N3, can become intractable, even for triatomics. Sparse iterative approaches have shown to be a viable means for solving linear algebra problems with such large matrices [11] [12] [18] [21] -[25] , for matrix-vector products scale with the number of nonzero elements, thus reducing computational effort with increasing sparsity. Furthermore, storage of the entire
matrix is an important numerical consideration, given that the matrix dimensionality, N, scales exponentially with the number of dofs. Consequently, direct diagonalization routines such as Householder’s algorithm, for which memory requirements scale as N2, and computational effort as N3, can become intractable, even for triatomics. Sparse iterative approaches have shown to be a viable means for solving linear algebra problems with such large matrices [11] [12] [18] [21] -[25] , for matrix-vector products scale with the number of nonzero elements, thus reducing computational effort with increasing sparsity. Furthermore, storage of the entire 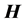 is not necessary, significantly reducing storage requirements. The sparsity and highly structured form of
is not necessary, significantly reducing storage requirements. The sparsity and highly structured form of 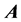 matrices would suggest the use of sparse iterative techniques, yet research has shown the
matrices would suggest the use of sparse iterative techniques, yet research has shown the 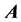 matrix to be a
matrix to be a
Figure 1. AB2 molecule (Model of an AB2 molecule as described by Jacobi coordinates).
Figure 2. A matrix form (A matrix form with greater than two degrees of freedom. This form is characterized by being block diagonal, with off-diagonal blocks being diagonal themselves. Note the self similar pattern of the diagonal blocks).
worst case scenario in many respects, that elicits poor performance from all standard iterative methods [26] -[28] . To this end, the algorithms developed in ScalIT address the shortcomings, and have proven to be effective and highly parallelizable.
ScalIT overcomes the above difficulties in part through the preconditioned inexact spectral transform (PIST) algorithm [12] -[14] . This approach calculates a window of states around a chosen energy by applying the Lanczos algorithm to , where
, where  is the identity, rather than to
is the identity, rather than to 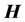 itself. This shift-and-invert strategy extremizes the states close to energy
itself. This shift-and-invert strategy extremizes the states close to energy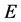
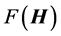
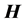
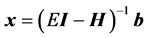
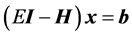
It is well known that when solving a system of linear equations 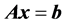
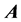
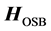
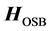
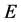
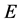
3. Using ScalIT
In the context of bound rovibrational spectroscopy calculations for triatomic molecules, a typical ScalIT calculation will proceed in three (or four) separate stages:
1) Compute 1D phase space optimized (PSO) effective potentials (defined shortly) and basis sets for radial coordinates, r and R.
2) Construct 4D (Coriolis-coupled) rovibrational Hamiltonian matrix for given J and ϵ.
3) Solve the Hamiltonian matrix eigenproblem to compute rovibrational energy levels and (optionally) wavefunctions.
4) (optional) Create plotting data for specified rovibrational wavefunctions.
Each stage has a different high-level ScalIT module (or set of modules) associated with it, as well as its own short input file (typically 6 - 10 lines each).
Stage 1 above is problem—(i.e. potential energy surface (PES)-) specific. For each of a very large number of uniformly-spaced points for a given radial coordinate (e.g. r), the PES is globally minimized with respect to all other coordinates, to determine the value of the radial PSO effective potential at that point [e.g.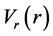
Stage 2 employs one of three standard ScalIT modules—depending on whether the triatomic molecule of interest is of the AB2 form (i.e. two identical nuclei) or not, and if so, whether the even- or odd-permutation symmetry block is desired. In the input file, the user specifies J, ϵ, the PSO DVR basis size for both radial coordinates, r and R, and the maximum j value to use in the basis expansion, jmax. j is the body-fixed analog of J. Radial PSO DVRs of the specified sizes are constructed using the PSO VBR data previously computed in Stage 1. The bend-angle basis functions are automatically combined with the appropriate body-fixed rotational states, with optional application of energy truncation to the combined bend-rotation states (K truncation could also be applied). The various components of the full-dimensional, but sparse, rovibrational Hamiltonian matrix are then stored in separate data files (one for the radial PSO DVR grid point and matrix data, the other for the angular contributions). Stage 2 must be repeated for each separate convergence calculation—i.e., for each distinct set of basis parameters used. However, it is quite fast for triatomic systems, typically requiring only seconds to minutes of CPU time.
Stage 3, the “meat” of the ScalIT package, employs but a single standard module—designed to accommodate calculations of arbitrary symmetry and dimensionality (i.e., tetraatomic and pentaatomic calculations use this same module). The coordinates may also be combined into “layers”, if desired. The first phase of Stage 3 is the OSB preconditioner construction phase for which the default choice is to treat the radial coordinates as separate inner coordinate layers, and the combined bend-rotation states as a single outermost layer. For standard OSB preconditioning, no user parameters are required, although more sophisticated preconditioning schemes do require this (e.g., specification of the Wyatt window center and width, for OSBW preconditioning). In the second phase of Stage 3, the PIST method is used to compute a predetermined number of rovibrational eigenstate energies (and wavefunctions if desired) in the vicinity of a specified central energy, E, to within a predetermined (iterative) error (generally chosen to be far smaller than the basis set convergence error). Note that wavefunction calculations do not require a second PIST calculation. Also, M is small (typically ~2 times the desired number of states) thus rendering explicit reorthogonalization feasible. As for the QMR component of PIST, it is hoped that preconditioning has reduced L to a manageably small value. As input for stage 3, users specify the number of (possibly combined) coordinates, the energy window over which rovibrational states are to be computed, and various other parameters as described above. An output file is generated that lists the computed rovibrational eigenvalues. Also, various optional data files may be written—as may be used, e.g., for wavefunction plotting purposes in Stage 4.
The optional Stage 4 is executed if wavefunction plots are desired. All of the requisite data may be found in the optional output files of Stage 3. However, this data is not presented in a form that would be useful for plotting via standard packages such as Mathematica. It is the purpose of Stage 4 to extract and output such information, for selected wavefunctions. Specifically, this module will output explicit values for the eigenstate wavefunction density, as a function of the four coordinates, R, r, θ, and K. An optional summation over all K values can also be computed, as well as a transformation from Jacobi to hyperspherical coordinate systems.
The four stages described above are logical, and easy to use in practice. To date, even undergraduate and high school students (with some guidance) have been able to converge triatomic rovibrational state calculations using ScalIT as described above.
4. Applications
Although ScalIT can, in general, be used to solve a variety of physical problems, current application and development have been limited to calculating bound rovibrational spectra for triatomic systems. We give here only a few examples of the recent applications.
In a recent publication [30] , the bound states of the hydroperoxl radical, HO2, were calculated up to the highest possible total angular momentum value, 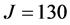
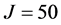
All rovibrational states were converged to an accuracy of 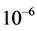
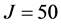
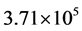
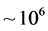
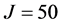
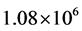
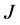
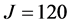
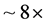
ScalIT has also been applied to a series of rare gas clusters [7] [19] [20] : Ne3, Ne2Ar, Ar2Ne, Ar3, as well as the neon tetramer, Ne4. Study of rare gas clusters in chemical physics gives insight to a variety of phenomena, including Van der Waals interactions, solvation processes, and phase change boundaries. Computationally, rare gas clusters can be fairly accurately described by pair-wise potentials, obviating the development of a PES. Despite this, their inherent long range interactions yield extremely “floppy” behavior, and typically exhibit a high density of states, both contributing to the difficulty in computation. All rovibrational bound states were computed up to dissociation for each of the respective systems. Due to the relatively heavy nature of Ar3, the difficulty of computing high lying states near dissociation is heavily exacerbated, yet was still accomplished with a modest computational allocation and will be the subject for an upcoming publication. The neon tetramer is currently under investigation by the authors and will be, to the authors’ knowledge, the most comprehensive rovibrational bound state calculation of rare gas clusters reported to date.
5. Conclusion
The poor performance exhibited from standard iterative sparse matrix solvers applied to the A matrix has fueled the development of ScalIT. From the ground up, ScalIT has been developed to be a highly parallelizable, robust iterative sparse matrix eigensolver. Furthermore, because parallelization is applied at the level of the matrix- vector product, any level of the software suite can be utilized by the broader community, though we focus here on the high-level use of calculating rovibrational spectra for triatomic molecules. By following the procedure given above, a non-expert user can easily compute such spectra. ScalIT has been applied to many molecular applications, and has proven itself even in high-density-of-states regimes. ScalIT is available free of charge upon request to the authors.
Acknowledgements
This work was largely supported by both a research grant (CHE-1012662) and a CRIF MU instrumentation grant (CHE-0840493) from the National Science Foundation. Additional support from The Robert A. Welch Foundation (D-1523) is also acknowledged, as well as from the Office of Advanced Scientific Computing Research, Mathematical, Information, and Computational Sciences Division of the US Department of Energy under contract DE-FG03-02ER25534. We also gratefully acknowledge the following entities for providing access and technical support for their respective computing clusters: the Texas Tech University High Performance Computing Center, for use of the Hrothgar facility; NSF CHE-0840493 and the Texas Tech University Department of Chemistry and Biochemistry, for use of the Robinson cluster; Carlos Rosales-Fernandez and the Texas Advanced Computing Center, for use of the Lonestar facility. Calculations discussed in this paper were performed using the ScalIT suite of parallel codes.
References
- Chen, W. and Poirier, B. (2010) Quantum Dynamical Calculation of All Rovibrational States of HO2 for Total Angular Momentum J = 0 − 10. Journal of Theoretical and Computational Chemistry, 9, 435-469. http://dx.doi.org/10.1142/S0219633610005815
- Poirier, B. (1998) Quantum Reactive Scattering for Three Body Systems via Optimized Preconditioning, as Applied to the O+HCl Reaction. The Journal of Chemical Physics, 108, 5216-5224. http://dx.doi.org/10.1063/1.475958
- Chen, W. and Poirier, B. (2006) Parallel Implementation of Efficient Preconditioned Linear Solver for Grid-Based Applications in Chemical Physics. I: Block Jacobi Diagonalization. Journal of Computational Physics, 219, 185-197. http://dx.doi.org/10.1016/j.jcp.2006.04.012
- Chen, W. and Poirier, B. (2006) Parallel Implementation of Efficient Preconditioned Linear Solver for Grid-Based Applications in Chemical Physics. II: QMR Linear Solver. Journal of Computational Physics, 219, 198-209. http://dx.doi.org/10.1016/j.jcp.2006.03.03
- Chen, W. and Poirier, B. (2010) Parallel Implementation of an Efficient Preconditioned Linear Solver for Grid-Based Applications in Chemical Physics. III: Improved Parallel Scalability for Sparse Matrix Vector Products. Journal of Parallel and Distributed Computing, 70, 779-782. http://dx.doi.org/10.1016/j.jpdc.2010.03.008
- Chen, W. and Poirier, B. (2010) Quantum Dynamics on Massively Parallel Computers: Efficient Numerical Implementation for Preconditioned Linear Solvers and Eigensolvers. Journal of Theoretical and Computational Chemistry, 9, 825-846. http://dx.doi.org/10.1142/S021963361000602X
- Yang, B., Chen, W. and Poirier, B. (2011) Rovibrational Bound States of Neon Trimer: Quantum Dynamical Calculation of All Eigenstate Energy Levels and Wavefunctions. The Journal of Chemical Physics, 135, Article ID: 094306. http://dx.doi.org/10.1063/1.3630922
- Poirier, B. and Light, J.C. (1999) Phase Space Optimization of Quantum Representations: Direct-Product Basis Sets. The Journal of Chemical Physics, 111, 4869-4885. http://dx.doi.org/10.1063/1.479747
- Poirier, B. and Light, J.C. (2001) Phase Space Optimization of Quantum Representations: Three-Body Systems and the Bound States of HCO. The Journal of Chemical Physics, 114, 6562-6571. http://dx.doi.org/10.1063/1.1354181
- Poirier, B. (2001) Phase Space Optimization of Quantum Representations: Non-Cartesian Coordinate Spaces. Foundations of Physics, 31, 1581-1610. http://dx.doi.org/10.1023/A:1012642832253
- Bian, W. and Poirier, B. (2003) Accurate and Highly Efficient Calculation of the O(1D)HCl Vibrational Bound States Using a Combination of Methods. Journal of Theoretical and Computational Chemistry, 2, 583-597. http://dx.doi.org/10.1142/S0219633603000768
- Huang, S.W. and Carrington Jr., T. (2000) A New Iterative Method for Calculating Energy Levels and Wave Functions. The Journal of Chemical Physics, 112, 8765-8771. http://dx.doi.org/10.1063/1.481492
- Poirier, B. and Carrington Jr., T. (2001) Accelerating the Calculation of Energy Levels and Wave Functions Using an Efficient Preconditioner with the Inexact Spectral Transform Method. The Journal of Chemical Physics, 114, 9254- 9264. http://dx.doi.org/10.1063/1.1367396
- Poirier, B. and Carrington Jr., T. (2002) A Preconditioned Inexact Spectral Transform Method for Calculating Resonance Energies and Widths, as Applied to HCO. The Journal of Chemical Physics, 116, 1215-1227. http://dx.doi.org/10.1063/1.1428752
- Poirier, B. and Miller, W.H. (1997) Optimized Preconditioners for Green Function Evaluation in Quantum Reactive Scattering Calculations. Chemical Physics Letters, 265, 77-83. http://dx.doi.org/10.1016/S0009-2614(96)01408-X
- Poirier, B. (1997) Optimal Separable Bases and Series Expansions. Physical Review A, 56, 120-130. http://dx.doi.org/10.1103/PhysRevA.56.120
- Poirier, B. (2000) Efficient Preconditioning Scheme for Block Partitioned Matrices with Structured Sparsity. Numerical Linear Algebra with Applications, 7, 715-726. http://dx.doi.org/10.1002/1099-1506(200010/12)7:7/8<715::AID-NLA220>3.0.CO;2-R
- Wyatt, R.E. (1995) Matrix Spectroscopy: Computation of Interior Eigenstates of Large Matrices Using Layered Iteration. Physical Review E, 51, 3643-3658. http://dx.doi.org/10.1103/PhysRevE.51.3643
- Yang, B. and Poirier, B. (2012) Quantum Dynamical Calculation of Rovibrational Bound States of Ne2Ar. Journal of Physics B, 45, Article ID: 135102. http://dx.doi.org/10.1088/0953-4075/45/13/135102
- Yang, B. and Poirier, B. (2012) Rovibrational Bound States of the Ar2Ne Complex. Journal of Theoretical and Computational Chemistry, 12, Article ID: 1250107. http://dx.doi.org/10.1142/S0219633612501076
- Lung, C. and Leforestier, C. (1989) Accurate Determination of Potential Energy Surface for CD3H. The Journal of Chemical Physics, 90, 3198-3203. http://dx.doi.org/10.1063/1.455871
- Bentley, J., Brunet, J., Wyatt, R.E., Friesner, R. and Leforestier, C. (1989) Quantum Mechanical Study of the SEP Spectrum for HCN. Chemical Physics Letters, 161, 393-400. http://dx.doi.org/10.1016/0009-2614(89)85104-8
- Bramley, M. and Carrington Jr., T. (1993) A General Dicrete Variable Method to Calculate Vibrational Energy Levels of Three and Four Atom Molecules. The Journal of Chemical Physics, 99, 8519-8541. http://dx.doi.org/10.1063/1.465576
- Bramley, M. and Carrington Jr., T. (1994) Calculation of Triatomic Vibrational Eigenstates: Product or Contracted Basis Sets, Lanczos or Conventional Eigensolvers? What is the Most Efficient Combination? The Journal of Chemical Physics, 101, 8494-8507. http://dx.doi.org/10.1063/1.468110
- Wang, X. and Carrington Jr., T. (2001) A Symmetry-Adapted Lanczos Method for Calculating Energy Levels with Different Symmetries from a Single Set of Iterations. The Journal of Chemical Physics, 114, 1473-1477. http://dx.doi.org/10.1063/1.1331357
- Geus, R. and Röllin, S. (2001) Towards a Fast Parallel Sparse Symmetric Matrix-Vector Multiplication. Parallel Com- puting, 27, 883-896. http://dx.doi.org/10.1016/S0167-8191(01)00073-4
- http://www.mcs.anl.gov/petsc/
- Press, W.H., Flannery, B.P., Teukolsky, S.A. and Vetterling, W.T. (1989) Numerical Recipes. Cambridge University Press, Cambridge.
- Colbert, D.T. and Miller, W.H. (1992) A Novel Discrete Variable Representation for Quantum Mechanical Reactive Scattering via the S-Kohn Method. The Journal of Chemical Physics, 96, 1982-1991. http://dx.doi.org/10.1063/1.462100
- Petty, C. and Poirier, B. (2013) Quantum Dynamical Calculation of Bound Rovibrational States of HO2 up to Largest Possible Total Angular Momentum, J ≤ 130. The Journal of Chemical Physics A, 117, 7280-7297. http://dx.doi.org/10.1021/jp401154m
- Zhang. H. and Smith, S. (2001) Calculation of Product State Distributions from Resonance Decay via Lanczos Subspace Filter Diagonalization: Application to HO2. The Journal of Chemical Physics, 115, 5751-5758. http://dx.doi.org/10.1063/1.1400785
- Zhang, H. and Smith, S. (2003) Calculation of Bound and Resonance States of HO2 for Nonzero Total Angular Momentum. The Journal of Chemical Physics, 118, 10042-10050. http://dx.doi.org/10.1063/1.1572132
- Zhang, H. and Smith, S. (2004) Converged Quantum Calculations of HO2 Bound States and Resonances for J = 6 and 10. The Journal of Chemical Physics, 120, 9583-9593. http://dx.doi.org/10.1063/1.1711811
- Zhang, H. and Smith, S. (2005) Unimolecular Rovibrational Bound and Resonance States for Large Angular Momentum: J = 20 Calculations for HO2. The Journal of Chemical Physics, 123, Article ID: 014308. http://dx.doi.org/10.1063/1.1949609
- Zhang, H. and Smith, S. (2006) HO2 Ro-Vibrational Bound State Calculations for Large Angular Momentum: J = 30; 40 and 50. The Journal of Chemical Physics, 110, 3246-3253. http://dx.doi.org/10.1021/jp0582336