Applied Mathematics
Vol.4 No.10B(2013), Article ID:38061,7 pages DOI:10.4236/am.2013.410A2012
On the Numerical Solutions of One and Two-Stage Model of Carcinogenesis Mutations with Time Delay and Diffusion*
Department of Mathematics, COMSATS Institute of Information Technology, Islamabad, Pakistan
Email: ishtiaqali@comsats.edu.pk
Copyright © 2013 Ishtiaq Ali. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 15, 2013; revised September 15, 2013; accepted September 23, 2013
Keywords: Carcinogenesis Mutations; Delay and Diffusion; Spectral Postprocessing; Numerical Simulations
ABSTRACT
In this paper, we focused on numerical solutions of carcinogenesis mutations models that are based on reaction-diffusion systems and Lotka-Volterra food chains. We consider the case with one and two-stages of mutations with appropriate initial conditions and the zero-flux boundary conditions. The main purpose is to construct a stable discretization scheme, which allows much accuracy than those of a standard approach. To this end, we use the spectral method to postprocess numerical solutions for the proposed model by using some classical methods for solving differential equations. The implementation of the algorithm is simple and it does not need to solve the linear or nonlinear system (in case the model is nonlinear). We simulate the one and two-stage carcinogenesis mutations model and compared the results with previously published ones.
1. Introduction
The struggle for finding an effective and permanent cure for tumor continues to challenge scientists has been made by a lot of progresses in discovering new methodologies which are helpful in successful treatments to reduce and even clear tumors. Mathematical modeling is one of the tools to improve the cancer therapy. Carcinogenesis is a very complicated process and one need a comprehensive study to fully understand it. Tumors are derived from one or more normal cells that have undergone malignant transformation. The immune response to tumors depends on how antigenic the tumor is. A cell that has undergone significant mutation results in a tumor is easier to be recognized as foreign (i.e. more antigenic) than one that differs only slightly from a healthy cell [1]. For different types of cancers, it is possible to divide the process into different number of stages, normally between 4 and 7 stages, which depends on the type of tumor [2].
In this paper, we study a simple model of carcinogenesis mutations of DNA, which originally comes from [3] and was also studied in [4-9], which describe a process of carcinogenesis mutations with n different steps of mutations (from normal to malignant cells). The model is expressed in terms of system of partial differential equation, in which the latest stage of mutation has different forms depending on whether it has growth advantage in favorable or competitive conditions or disadvantage of growth in unfavorable and competitive conditions. For simplicity in this paper, we only consider the latest stage in unfavorable conditions, as in the case of favorable conditions there is no possibility to cure the disease without any treatment. For more details we refer to [10,11].
The current work provides the computational and implementational details needed to study the dynamics of these equations [12]. A detailed analysis of the one-stage model equations was undertaken in [4]. We use spectral methods to postprocess numerical solutions, which use the numerical solutions of a lower order method to serve as starting value of the spectral methods. The iteration uses the Gauss-Seidel type strategy, which can be very useful in terms of improving the accuracy of the numerical solutions. In particular for the problems in which accuracy is the only issue and some conservatives properties are even more important for large time simulation. Also there is no need to solve a linear or nonlinear system of equations as we do need in case of using some other numerical methods [13].
The paper is organized as follows. Section 2 and 3 is used for the description of models in detail. In Section 4 and 5 we describe in detail the spectral postprocessing approximation for the proposed models. Section 6 is used for the numerical simulations and discussions, followed by the concluding remarks in Section 7.
2. Formulation of the Model
Let us consider 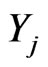 as a density of mutant cells of the j-th stage at position
as a density of mutant cells of the j-th stage at position 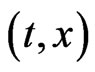 where
where 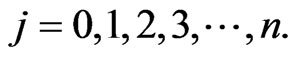 To develop a multistage model for mutant cells densities jY at stage
To develop a multistage model for mutant cells densities jY at stage ,
,  where
where  will be the initial stage,
will be the initial stage,  the density of intermediate stages, and
the density of intermediate stages, and 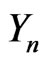 represents the density of the final stage. The system of equations for the density function is given by [2].
represents the density of the final stage. The system of equations for the density function is given by [2].
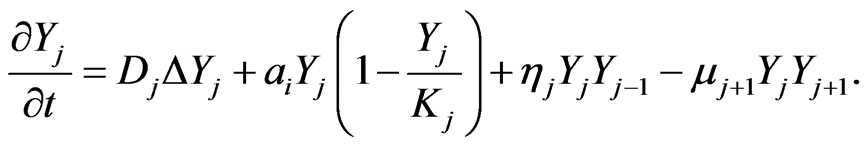 (1)
(1)
The final stage of mutation occurs when cancer cells become malignant and metastasize. We assume that for the malignant mutation in the final stage, the carrying capacity is unlimited; that is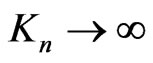 , thus Equation (1) becomes
, thus Equation (1) becomes
 (2)
(2)
3. Formulation of One and Two-Stage Mutation
The full blown developed malignant mutation can be described in the following system of the n-stage model, that is initial, benign, and malignant,
 (3)
(3)
After rescaling Equation (3) it can be written in the following simplified form
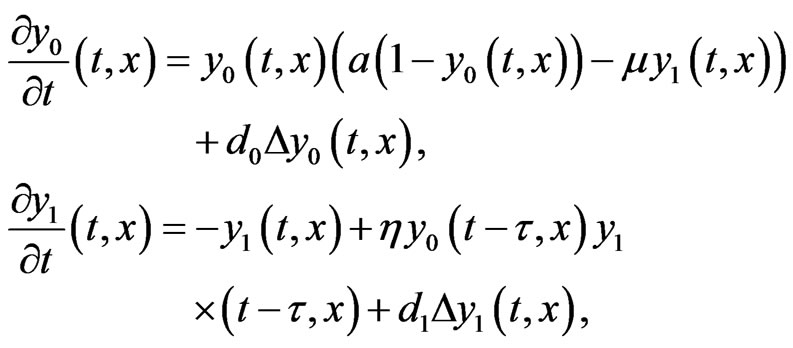 (4)
(4)
where  represents the density of normal cells at time
represents the density of normal cells at time  and position
and position 
 stands for malignant cells, constant
stands for malignant cells, constant

are positive, delay 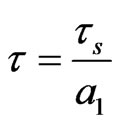 is non-negative and
is non-negative and
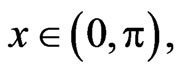 with the Neumann boundary and initial conditions
with the Neumann boundary and initial conditions
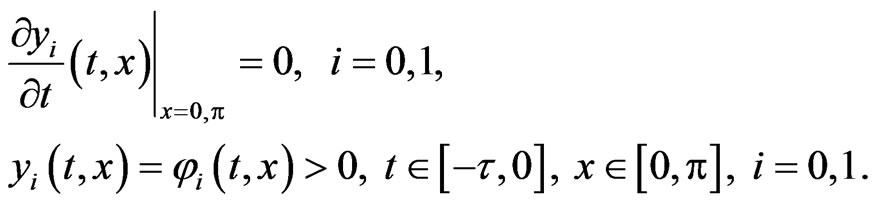
It is reasonable to consider interaction not only between cells on subsequent stages of mutations, and therefore we consider the following two-stage model
 (5)
(5)
subject to

4. Spectral Postprocessing Technique
In this section, we will describe in detail the spectral methods for Equations (4) and (5). We first use a finite difference scheme in time and spectral methods in space.
4.1. Finite Difference Scheme
Let 
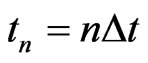 with
with 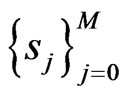 are are Legendre-Gauss-Lobatto points in
are are Legendre-Gauss-Lobatto points in  and
and
 Without losing any generality, we can choose
Without losing any generality, we can choose
 such that
such that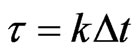 , where
, where 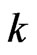 is an integer. Denote by
is an integer. Denote by
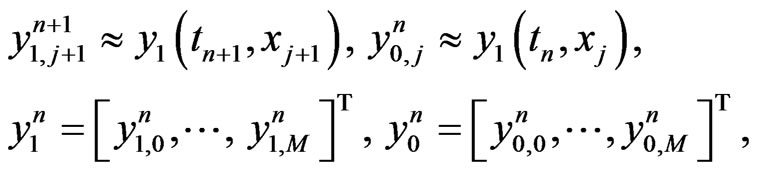
then the implicit difference scheme is given by enforcing Equation (4) at
at 
 (6)
(6)
where 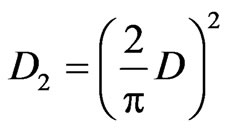 with
with  is the differential ma trix associated with Legendre-Gauss-Lobatto nodes, see [13] for details. Rearranging Equation (6) in terms of matrix form, we have
is the differential ma trix associated with Legendre-Gauss-Lobatto nodes, see [13] for details. Rearranging Equation (6) in terms of matrix form, we have
 (7)
(7)
where  means element-wise multiplication of two vectors. Here we should remark, considering the boundary conditions in Equation (4), that is the first and the last equation in the above equation, that is Equation (7) do not hold any more. Instead, we must replace those two equations by directly discretizing the boundary conditions respectively. Similarly the semi-implicit scheme for
means element-wise multiplication of two vectors. Here we should remark, considering the boundary conditions in Equation (4), that is the first and the last equation in the above equation, that is Equation (7) do not hold any more. Instead, we must replace those two equations by directly discretizing the boundary conditions respectively. Similarly the semi-implicit scheme for 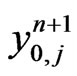 is given by
is given by
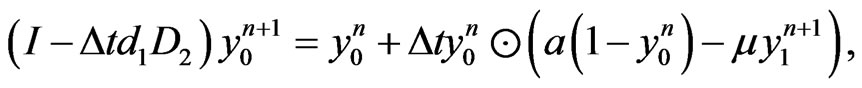 (8)
(8)
where we utilize the updated  in Equation (7). Moreover, to replace the first and the last equations in Equation (8), we also need to enforce the boundary conditions of
in Equation (7). Moreover, to replace the first and the last equations in Equation (8), we also need to enforce the boundary conditions of  that
that

Applying the same implicit and semi-implicit finite difference scheme to the two-stage mutation model, we have the following system
 (9)
(9)
where  are assumed to be integer for simplicity.
are assumed to be integer for simplicity.
In fact, we can deal with any  by interpolation if there is no suitable
by interpolation if there is no suitable  such that
such that 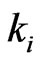 be integers. Moreover, to satisfy the boundary conditions which is similar to one-stage mutation model, we can replace the first and the last equations in each matrix form by
be integers. Moreover, to satisfy the boundary conditions which is similar to one-stage mutation model, we can replace the first and the last equations in each matrix form by
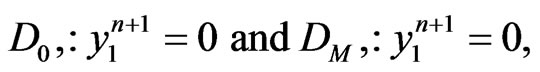
for  respectively.
respectively.
5. Postprocessing
It is well known that backward Euler finite difference scheme in time direction is of the first order accuracy, which is much worse than the spectral accuracy in spatial direction. Therefore, to achieve the balance between the errors in two directions, we use spectral postprocessing in [13] to enhance the accuracy in time direction based upon the backward Euler finite difference scheme.
To describe the time marching scheme clearly, we give some notations as follows. Split the time interval 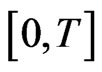 into several subintervals, i.e.,
into several subintervals, i.e., 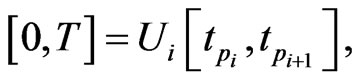 for simplicity we can take
for simplicity we can take  Let
Let
 with
with 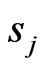 given above as LegendreGauss-Lobatto points in
given above as LegendreGauss-Lobatto points in .
.
Integrating Equation (4) from  to
to 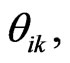 we get
we get
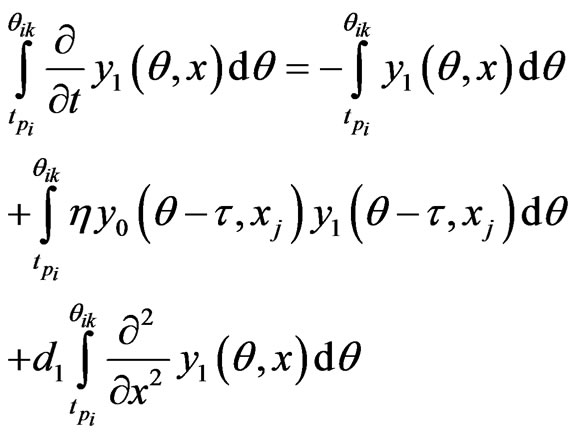 (10)
(10)
using the  -point Legendre Gauss-Lobatto quadrature formula relative to the Legendre weights on the right hand side of Equation (10) gives
-point Legendre Gauss-Lobatto quadrature formula relative to the Legendre weights on the right hand side of Equation (10) gives
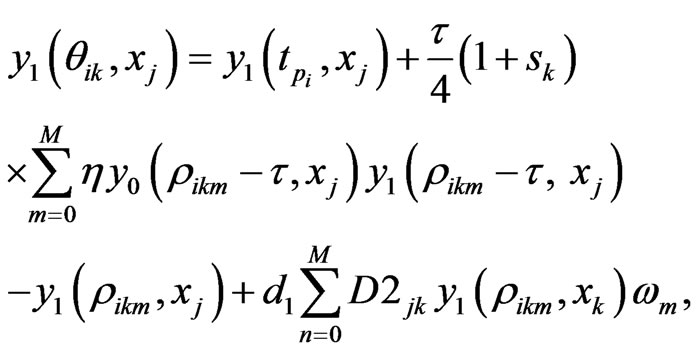 (11)
(11)
where 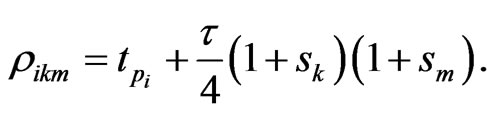 In the above formula, to explicitly update
In the above formula, to explicitly update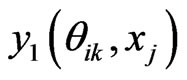 , we need to evaluate
, we need to evaluate  by some approximations. Fortunately, we have the Euler scheme solution (7) as an initial approximation and then interpolation to the LegendreGauss-Lobatto points in
by some approximations. Fortunately, we have the Euler scheme solution (7) as an initial approximation and then interpolation to the LegendreGauss-Lobatto points in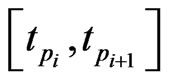 . Denote by
. Denote by 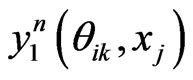 the n-th loop of post-processing solution, whereas for
the n-th loop of post-processing solution, whereas for , it is the linear interpolation of the solution (7). The full numerical scheme for Equation (4) is given by
, it is the linear interpolation of the solution (7). The full numerical scheme for Equation (4) is given by
 (12)
(12)
where  is the e-th Lagrangian interpolation polynomials associated with Legendre-Gauss-Lobatto points. Here we remark that in Equation (12) the updated information of
is the e-th Lagrangian interpolation polynomials associated with Legendre-Gauss-Lobatto points. Here we remark that in Equation (12) the updated information of 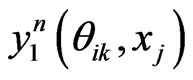 is immediately used to obtain
is immediately used to obtain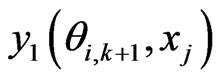 . Similarly, we can get the spectral post processing scheme for
. Similarly, we can get the spectral post processing scheme for  in Equation (4):
in Equation (4):
 (13)
(13)
where
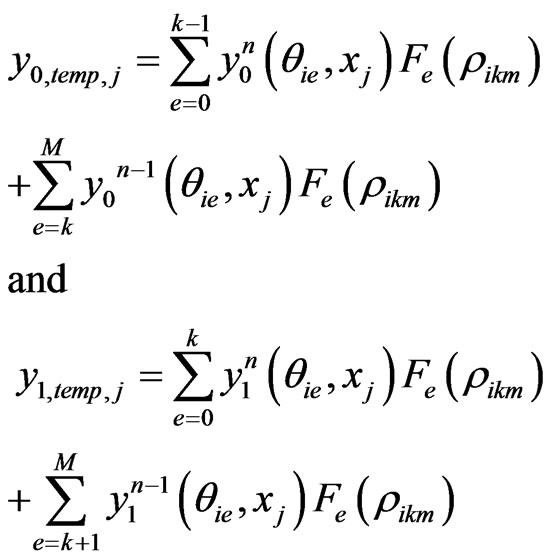
For the sake of compactness, we shall not give the full spectral post processing scheme for the two stage Equation (5) here. However, the idea is same as the one stage model. Instead, we give an algorithm to implement the spectral post processing scheme in detail.
Algorithm 5.1 (Spectral Post-Processing)
1) Initialize  by interpolation from Equations (7) and (8)
by interpolation from Equations (7) and (8)
2) For 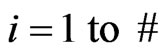 of subintervals
of subintervals
3) For  to # of loops on post processing
to # of loops on post processing
4) For 
5) 
6) Compute  by Equation (12)
by Equation (12)
7) Compute 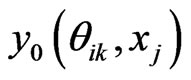 by Equation (13)
by Equation (13)
8) End 
9) End 
10) End 
6. Numerical Simulation and Discussion
In the following, some numerical simulations were carried out. In our computations we use the Legendre-Gauss quadrature with weights

In case of one-stage model the initial functions 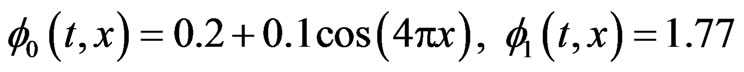 for healthy and cancer cells respectively and the parameters value
for healthy and cancer cells respectively and the parameters value
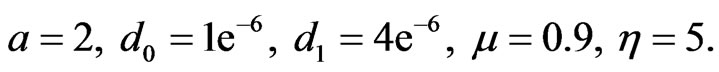 (14)
(14)
and for the two-stage model, we use
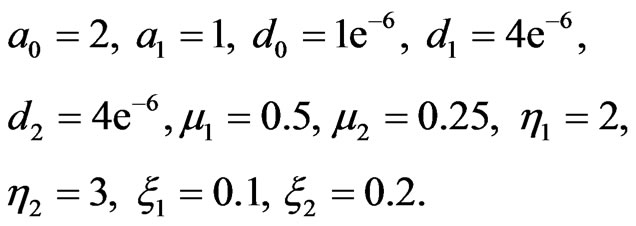 (15)
(15)
with

We start our simulation for the one-stage model, which is system of Equation (4) with small delay in which the steady state is positive; we observe the oscillatory behavior of the system with different mode of frequencies. The oscillation is then smooth because of the steady state (Figures 1 and 2). Increasing the delay term and fixing the other parameters, one can observe a very strong oscillatory behavior of the system. For a very large value of delay term, the solution behaves like traveling waves (Figures 3 and 4). As the dynamics of the system is period, it suggests that traveling wave solutions appear for the system with delay and diffusion. The same was observed for the two-stage model, which is system Equation (5) (Figures 5-10). In conclusion, we can say that the stability switch is only because of the increasing in delay and the diffusion itself cannot destabilize the system.

Figure 1. Simulated solution of system (4) for 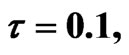 using the parameters values of Equation (14).
using the parameters values of Equation (14).

Figure 2. Simulated solution of system (4) for 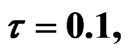 using the parameters values of Equation (14).
using the parameters values of Equation (14).

Figure 3. Simulated solution of system (4) for 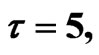 using the parameters values of Equation (14).
using the parameters values of Equation (14).
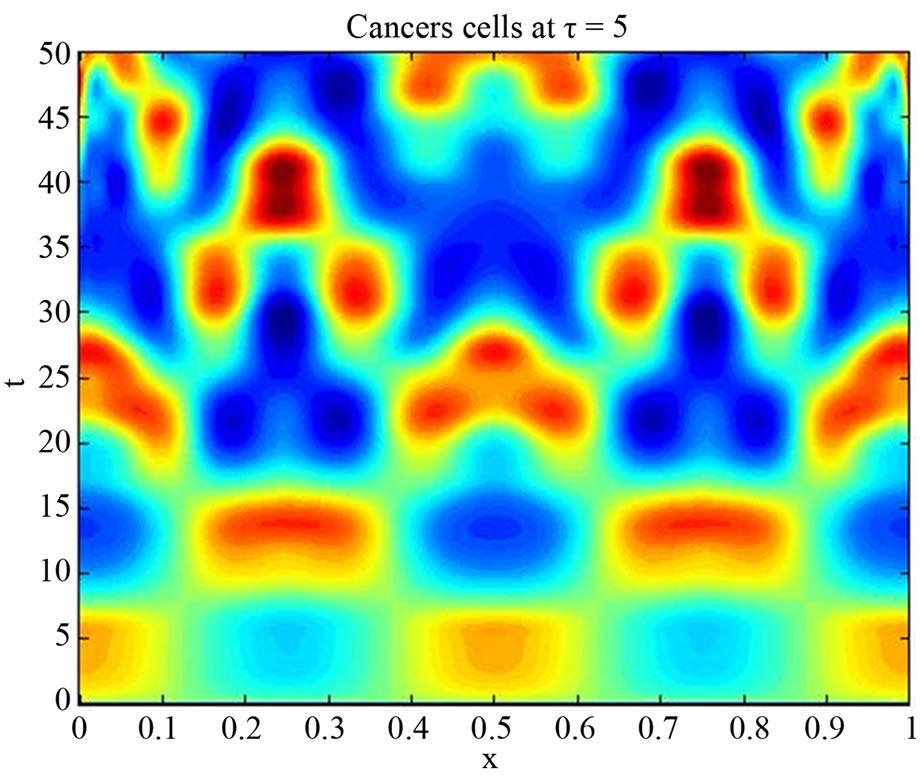
Figure 4. Simulated solution of system (4) for 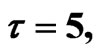 using the parameters values of Equation (14).
using the parameters values of Equation (14).

Figure 5. Simulated solution of system (5) for 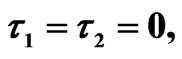 using the parameters values of Equation (15).
using the parameters values of Equation (15).

Figure 6. Simulated solution of system (5) for  using the parameters values of Equation (15).
using the parameters values of Equation (15).

Figure 7. Simulated solution of system (5) for  using the parameters values of Equation (15).
using the parameters values of Equation (15).

Figure 8. Simulated solution of system (5) for 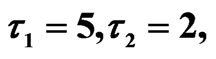 using the parameters value of Equation (15).
using the parameters value of Equation (15).

Figure 9. Simulated solution of system (5) for  using the parameters value of Equation (15).
using the parameters value of Equation (15).
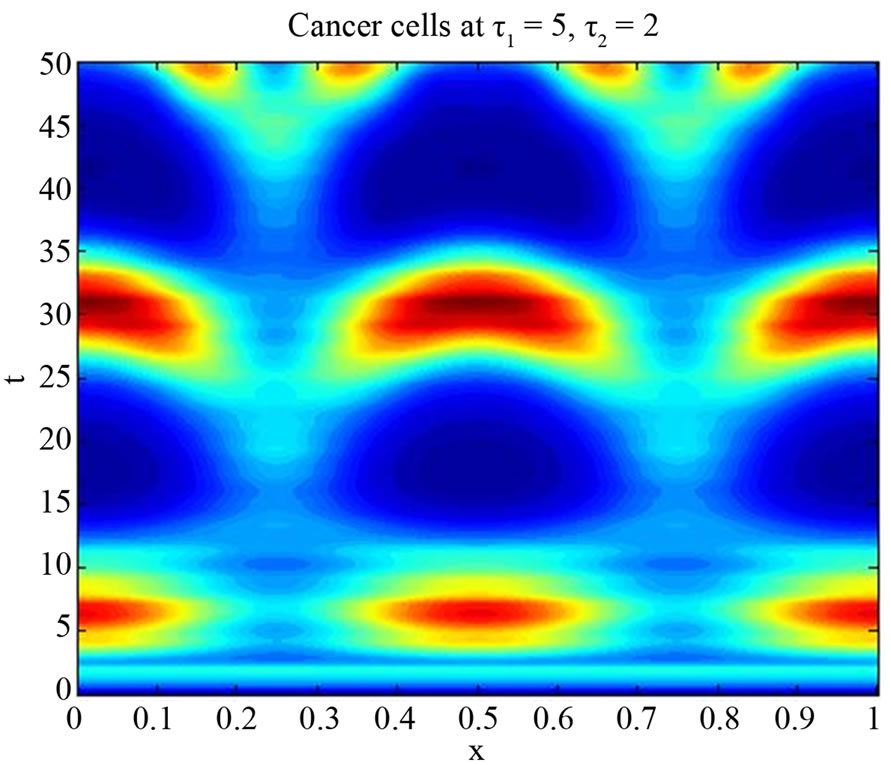
Figure 10. Simulated solution of system (5) for 
 using the parameters value of Equation (15).
using the parameters value of Equation (15).
7. Concluding Remarks It has been the aim of this paper to use a spectral postprocessing technique for the numerical solutions of one and two-stage model of carcinogenesis mutations with time delay and diffusion. The spectral postprocessing with the coarse-mesh symplectic initial guess produces high accurate approximate solution. It also saves a significant amount of computational time over the standard schemes. We compared the results obtained by simulateing the one and two-stage model with the available one and find it with good agreement. The future work includes the theoretical stability analysis of the proposed method and its extension to higher dimensions.
8. Acknowledgements
The author is very grateful to Professor Urszula Forys of the Institute of Applied Mathematics and Mechanics Faculty of Mathematics, Informatics and Mechanics University of Warsaw, Poland for her many discussions and Xu Xiang of MSU for his help in Algorithm.
REFERENCES
- J. C. Arciero, T. L. Jackson and D. E. Kirschner, “A Mathematical Model of Tumor-Immune Evasion and siRNA Treatment,” Discrete and Continuous Dynamical Systems, Series B, Vol. 4, No. 1, 2004, pp. 39-58.
- S. Kruś, “Pathological Anathomy,” PZWL, Warsaw, 2001.
- R. Ahangar and X. B. Lin, “Multistage Evolutionary Model for Carcinogenesis Mutations,” Electronic Journal of Differential Equations, Conference 10, 2003, pp. 33-53.
- M. Bodnar, U. Foryś, M. J. Piotrowska and J. Poleszczuk, “A Simple Model of Carcinogenesis Mutations with Time Delay and Diffusion,” Mathematical Biosciences and Engineering, Vol. 10, No. 3, 2013, pp. 861-872. http://dx.doi.org/10.3934/mbe.2013.10.861
- U. Foryś, “Biological Delay Systems and the Mikhailov Criterion of Stability,” Journal of Biological Systems, Vol. 12, No. 1, 2004, pp. 45-60. http://dx.doi.org/10.1142/S0218339004001014
- U. Foryś, “Stability Analysis and Comparison of the Models for Carcinogenesis Mutations in the Case of TwoStages of Mutations,” Journal of Applied Analysis, Vol. 11, No. 2, 2005, pp. 200-281. http://dx.doi.org/10.1515/JAA.2005.283
- U. Foryś, “Multi-Dimensional Lotka-Volterra System for Carcinogenesis Mutations,” Mathematical Methods in the Applied Sciences, Vol. 32, No. 17, 2009, pp. 2287-2308. http://dx.doi.org/10.1002/mma.1137
- U. Foryś, “Comparison of the Models for Carcinogenesis Mutations—One-Stage Case,” The Proceeding of the 5th National Conference on Mathematics, Applied to Biology and Medicine, Święty Krzyż, 2004.
- J. D. Murry, “Mathematical Biology 1: An Introduction,” Springer, Berlin, 2002.
- J. D. Murry, “Mathematical Biology 11: Special Models and Biochemical Applications, Interdisciplinary Applied Mathematics,” Springer, Berlin, 2003.
- J. D. Murry, “Mathematical Biology 11: Special Models and Biochemical Applications, Interdisciplinary Applied Mathematics,” Springer, Berlin, 2003.
- M. R. Garvie, “Finite-Difference Schemes for ReactionDiffusion Equations Modeling Redator-Prey Interactions in MATLAB,” Bulletin of Mathematical Biology, Vol. 69, No. 3, 2007, pp. 931-956. http://dx.doi.org/10.1007/s11538-006-9062-3
- T. Tang and X. Xu, “Accuracy Enhancement Using Spectral Postprocessing for Differential Equations and Integral Equations,” Communications in Computational Physics, Vol. 5, 2009, pp. 779-792.
NOTES
*Numerical solutions of one and two-stage model.
This work was carried out during the tenure of an ERCIM “Alain Bensoussan” Fellowship Programme. This Programme is supported by the Marie Curie Co-funding of Regional, National and International Programmes (COFUND) of the “European Commission”.

