Applied Mathematics
 Vol.4 No.1A(2013), Article ID:27504,9 pages DOI:10.4236/am.2013.41A038

Simplifying Stochastic Mathematical Models of Biochemical Systems

Silvana Ilie*, Samaneh Gholami

Department of Mathematics, Ryerson University, Toronto, Canada

Email: *silvana@ryerson.ca

Received October 9, 2012; revised November 9, 2012; accepted November 16, 2012

Keywords: Stochastic Modeling; Sensitivity Analysis; Model Reduction Techniques; Chemical Langevin Equation

ABSTRACT

Stochastic modeling of biochemical reactions taking place at the cellular level has become the subject of intense research in recent years. Molecular interactions in a single cell exhibit random fluctuations. These fluctuations may be significant when small populations of some reacting species are present and then a stochastic description of the cellular dynamics is required. Often, the biochemically reacting systems encountered in applications consist of many species interacting through many reaction channels. Also, the dynamics of such systems is typically non-linear and presents multiple time-scales. Consequently, the stochastic mathematical models of biochemical systems can be quite complex and their analysis challenging. In this paper, we present a method to reduce a stochastic continuous model of well-stirred biochemical systems, the Chemical Langevin Equation, while preserving the overall behavior of the system. Several tests of our method on models of practical interest gave excellent results.

1. Introduction

Mathematical modeling of biochemical reactions within a cell is crucial for understanding cellular dynamics [1]. Biological processes are often represented as systems of chemical reactions. In general, such processes involve many reacting species subject to many reaction channels. In systems with some low molecular populations, the random fluctuations associated with molecular interactions may be significant, as was observed experimentally [2,3]. Then, a deterministic model is not appropriate and stochastic models are needed for an accurate description of the reacting system behavior [4]. In many applications, the biochemical reactions evolve on widely different time scales. The presence of the multiple time-scale dynamics leads to mathematical stiffness. Stiffness poses great challenges in the simulation of the system dynamics. Moreover, many biochemical systems are non-linear which makes them more difficult to analyze. Thus, the stochastic mathematical models of biochemically reacting systems can be quite complex and their simulation computationally very demanding [5].

Often the goal is to understand some specific biological process of a complex biochemical network. Then, one needs to identify a reduced system of reactions which gives an accurate description of that process. Model reduction strategies may focus on reducing the number of reactions, the number of parameters or that of molecular species [6]. The existing model reduction schemes for deterministic models of chemical reaction systems may be grouped into sensitivity analysis methods [7], lumping methods [8,9] and time-scale analysis methods [10,11]. Lumping techniques lead to loss of information about particular species or reactions and thus the physical interpretation of the elementary reactions is lost. They may be appropriate when only limited information is available about specific reactions. Time-scale analysis applies to systems with rapid and slow reactions channels and is based on the assumption that the fast components are in a quasi-steady state. The slow dynamics is restricted to the algebraic constraints defining the equilibrium manifold of the fast components. The identification of the fast and slow reactions is required as well as estimations of the orders of magnitude of separation between them. Finally, sensitivity analysis may be employed to eliminate the reactions which are not important, if the parametric sensitivity with respect to their reaction rate constants are small. Then the physical insight offered by the elementary reactions, as opposed to group of reactions, is maintained. Much less work has been dedicated to designing model reduction strategies for the stochastic models of biochemical kinetics (see [12-14] and references therein).

Our contribution in this paper is to provide a novel method for reducing a stochastic continuous model of biochemical systems, the Chemical Langevin Equation.

The Chemical Langevin Equation (CLE) model [15] is an approximation of the discrete stochastic model of well-stirred biochemical kinetics, namely the Chemical Master Equation [16-19]. The CLE model is valid in the regime of large molecular numbers. The CLE is a system of Itô stochastic differential equations (SDE) with multiplicative noise of dimension equal to the number of reacting species. Our method is based on sensitivity analysis, which is a key tool for modeling and analyzing biochemical systems. Sensitivity analysis is widely used in quantifying the characteristics of the system [20], such as robustness with respect to perturbations in its parameters. These parameters include the reaction rate constants or the initial supplies of species. The study of the dependence of the system dynamics on its parameters is a critical problem in modeling biochemical systems, and in particular cellular dynamics, as usually some parameters for the kinetics of interaction are unknown or cannot be measured with accuracy. Also, in cellular environments, the supply of reactants may fluctuate. Sensitivity analysis studies the variation in molecular populations with respect to small changes in parameters. Thus, it enables the identification of the kinetic parameters with a negligible impact on the species of interest. Then, the reactions corresponding to these parameters can be removed from the system. By this procedure, the dynamics of interest in not altered while the system may be significantly reduced. Moreover, the reduced system may provide important physical insight and it is easier to analyze and simulate numerically.

The outline of the paper is as follows. Section 2 gives an introduction to the stochastic continuous modeling of well-stirred biochemical system. In Section 3, a technique for estimating sensitivities of the Chemical Langevin Equation is explored. In Section 4, we provide a model reduction strategy for the Chemical Langevin Equation, and we test this method on several models of interest in Section 5.

2. Chemical Langevin Equation

We present below a brief introduction to the stochastic modeling of chemical kinetics for well-stirred systems, in the regime of large molecular populations. The system is at thermal equilibrium in a constant volume. The chemically reacting system contains N biochemical species subject to M reactions. Under the assumptions above, the system dynamics can be described by the vector of states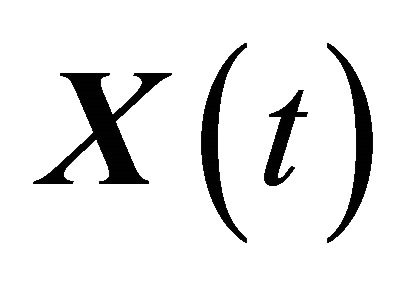, with component 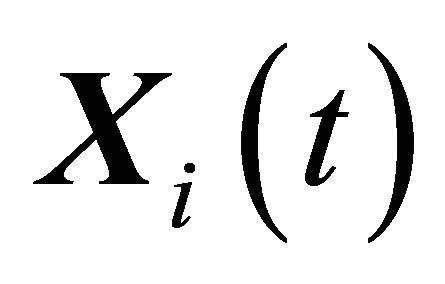being the number of Si molecules available at time t, for each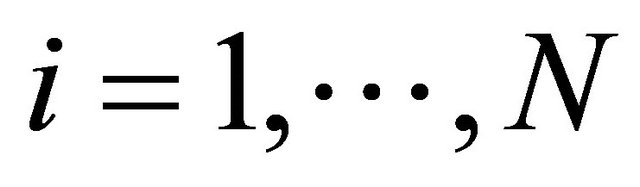. The dynamical state 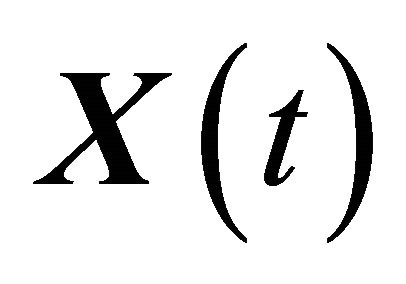is a Markov process.

Let us define 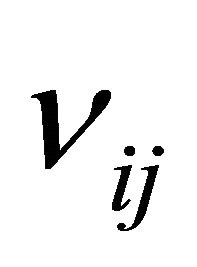to be the change in the number of molecules of species 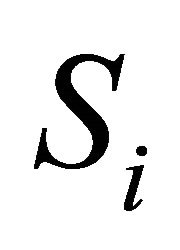caused by one reaction 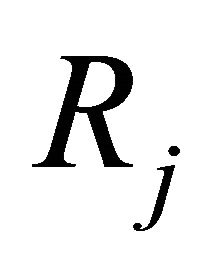and denote by the state-change vector characterizing the reaction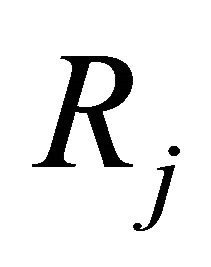. The matrix 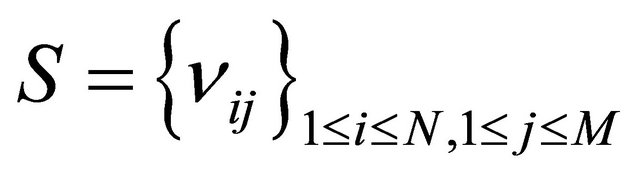is known as the stoichiometric matrix. Remark that each reaction 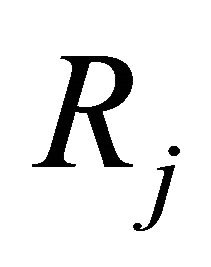produces a change in the system given by. In representing the reaction 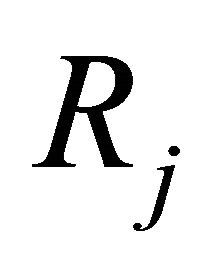an essential role is played by propensity function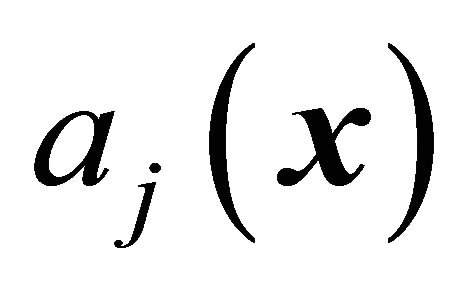. The propensity function is defined by 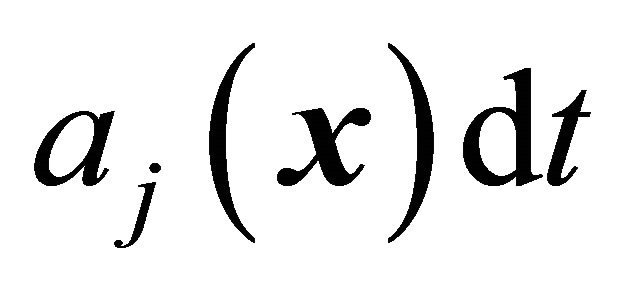at the given state, is the probability that one reaction will happen in the infinitesimal timeinterval. For example, for a reaction the propensity function is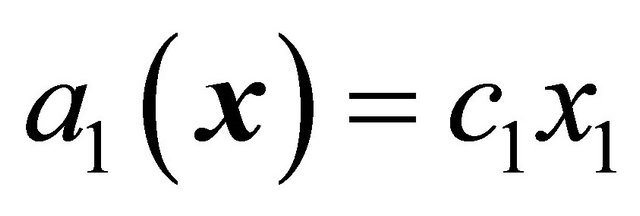, while for a reaction 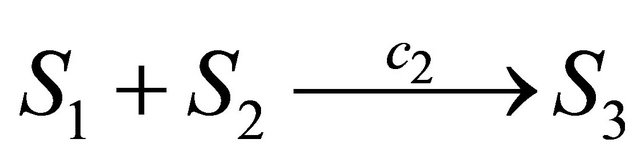the propensity function is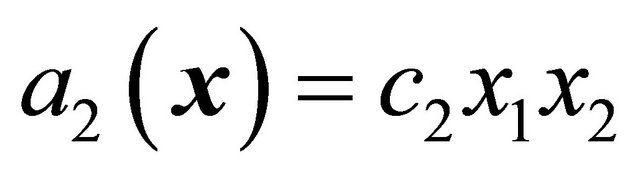. Finally, the associated propensity of the reaction 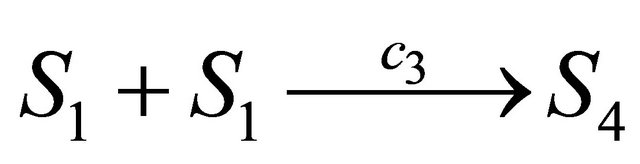is .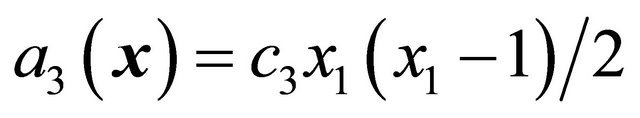

In addition, the following assumptions are made: there exists a time-step 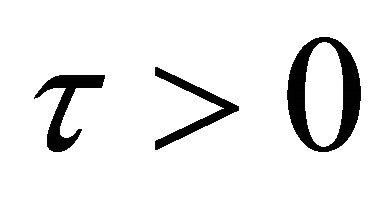such that 1) the step τ is small enough so that there is no significant change in any propensity during the interval,

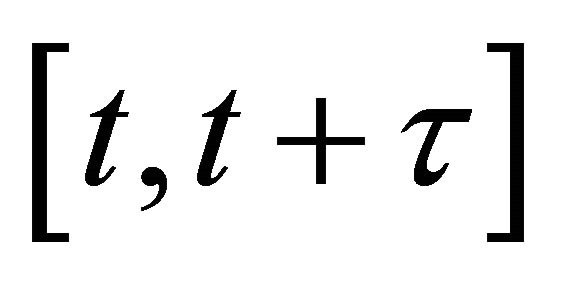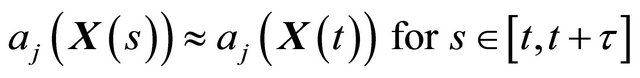(1)

for each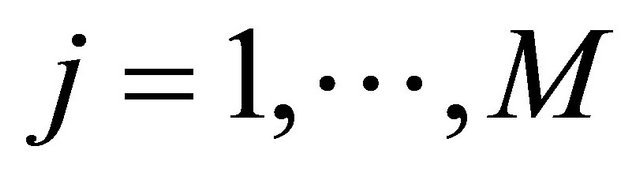, and 2) the step τ is sufficiently large so that the expected number of times each reaction 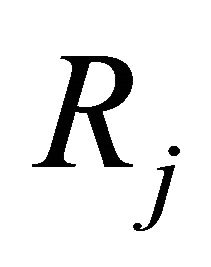fires during 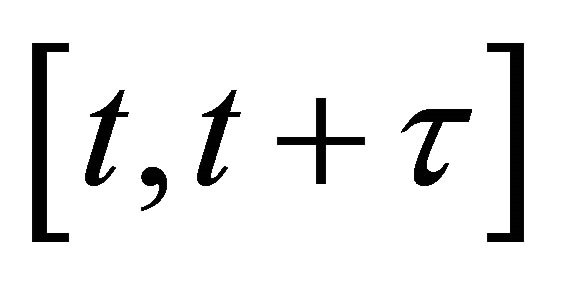is large. That is, each propensity should satisfy

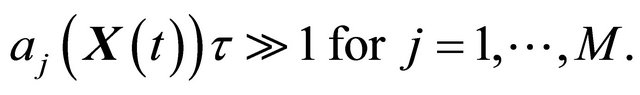(2)

Under the conditions above, the state vector obeys

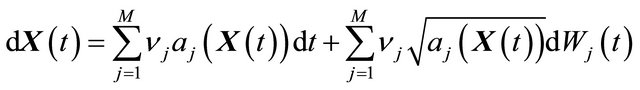(3)

where are independent Wiener processes for 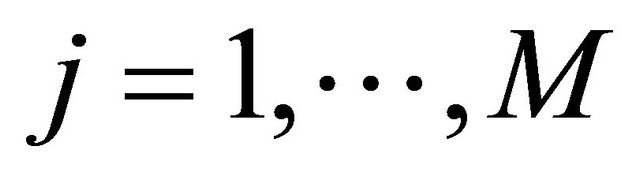. The Equation (3) is known as the Chemical Langevin Equation. This model is obtained when the requirements of 1) and 2) are satisfied. These conditions hold when each species has large molecular populations. The CLE is a system of Itô stochastic differential equations with multiplicative non-commutative noise, having one equation for each reacting species. The solution of the CLE model (3) should satisfy the initial condition

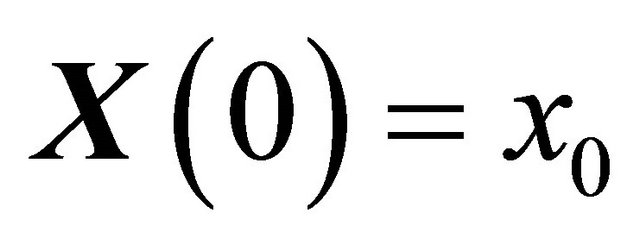(4)

imposed at the initial time.

Applying the expectation (denoted by) to the Chemical Langevin Equation (3) leads to

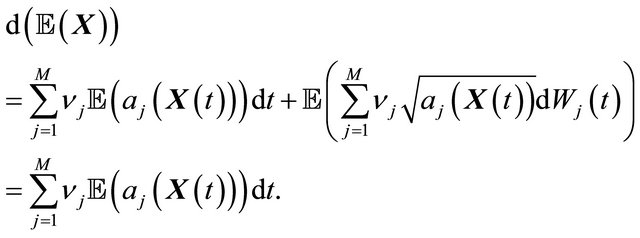
Now, dividing by, yields

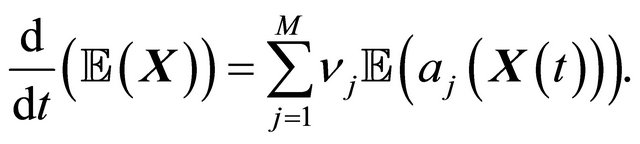
Notice that the CLE model reduces to the classical reaction rate equation model of the chemical kinetics, when all species have very large molecular numbers, in thermodynamic limit,

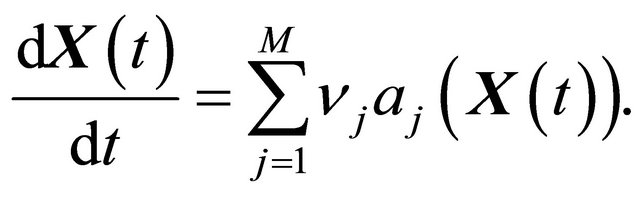(5)

The reaction rate equation is a system of ordinary differential equations of dimension equal to the number of biochemical species in the system. Generally, the reaction rate Equation (5) is written in terms of concentrations rather than in molecular population numbers.

3. Parametric Sensitivity of the Chemical Langevin Equation

Biochemical reaction models may depend on many parameters such as the kinetic rates, the initial amounts for each species or an uncertain environment. Some small changes in the parameters may considerably affect the system behavior. Hence, it is important to determine the influences of such changes. Sensitivity analysis studies the dependence of the system dynamics on the reaction rate parameters or the initial conditions. It is an essential analysis tool in kinetic modeling and it may be used to decide which parts of the model are actively contributing to the system behavior. Therefore, it plays a key role in assessing the accuracy of a model, in analyzing the model and in model reduction. In general, if X is differentiable with respect to a parameter p, the first order sensitivity is defined as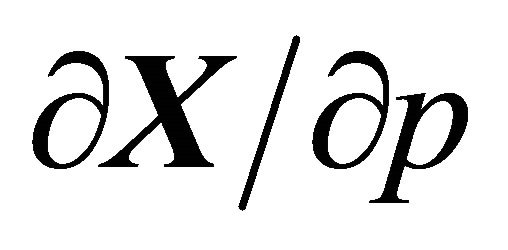. A large sensitivity suggests that the system may change dramatically when that parameter is perturbed. This shows that an accurate measurement of that parameter is necessary. By contrast, a small sensitivity indicates that the system is robust with respect to small variations in that parameter and thus rough estimations of the parameter value will be sufficient.

Below we discuss a numerical technique for computing the pathwise (strong) sensitivities with respect to the kinetic parameters for the Chemical Langevin Equation model. Pathwise derivative estimation of stochastic discrete models was studied for biochemical systems [21,22] as well for other areas of applications [23,24]. Since the CLE is a system of SDEs, then sensitivity analysis tools available for SDEs may apply for the Langevin model. The pathwise sensitivity technique presented here applies to diffusion processes [23].

Let 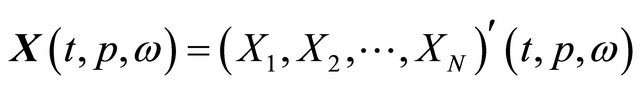be the solution of the CLE model (3) satisfying the initial condition (4). Here ω is a realization of the sample trajectories space Ω and p is a kinetic parameter. The pathwise sensitivity is interpreted as the pathwise derivative of 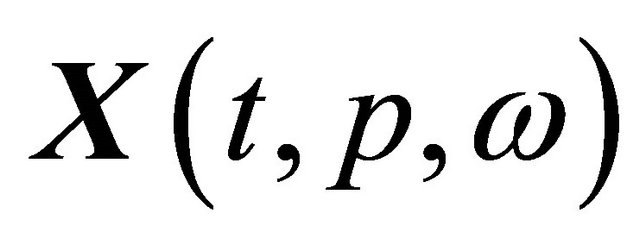with respect to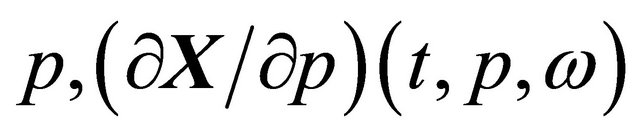, when the realization ω is fixed. The pathwise sensitivities may be obtained by differentiating, on each trajectory, the Chemical Langevin Equation (3) with respect to the parameter of interest, p. If the derivative 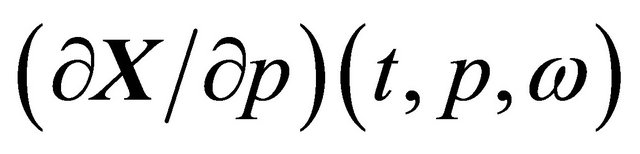exists with probability 1, we derive

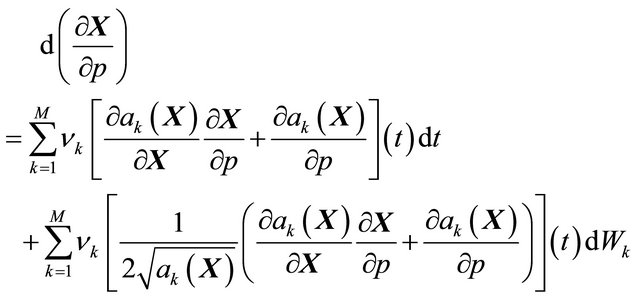(6)

Notice that 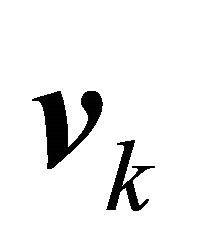does not depend on p for all 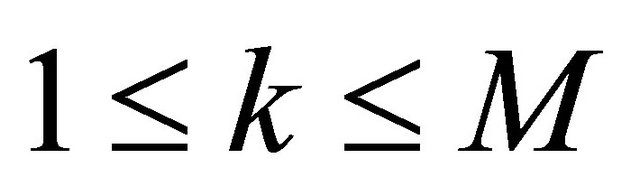, while the propensities are polynomials of degree at most one in the kinetic parameters thus 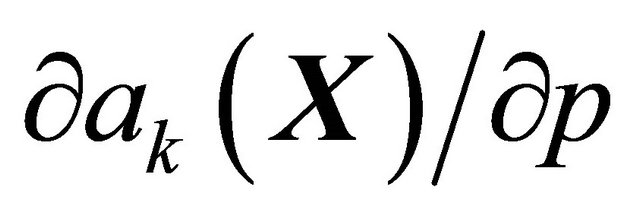does not depend on p explicitly. This approach to computing the pathwise sensitivities may be applied when each molecular species is bounded away from zero, which is true for biochemical systems in the Langevin regime.

In order to calculate the local sensitivities, the coupled system consisting of the CLE (3) and the auxiliary equations for the sensitivities (6) is solved to find the state vector 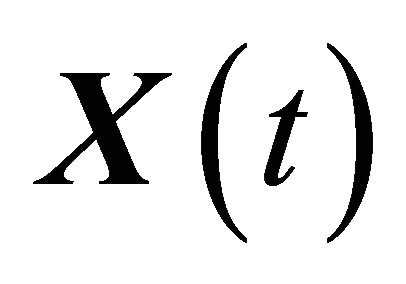and the sensitivities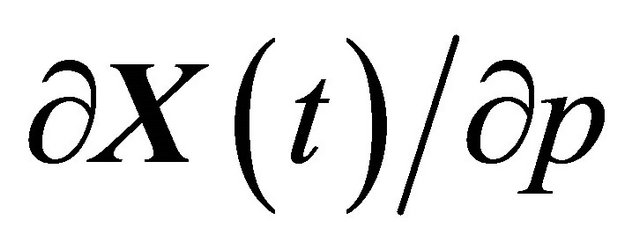. Remark that the combined system (3) and (6) has double size compared to the Chemical Langevin Equation, but has the same number of independent Wiener processes. Hence, it is generally almost twice as expensive to solve numerically as the CLE. The pathwise sensitivity analysis uses the exact derivative with respect to a parameter instead of numerical differentiation, as does a finite-difference scheme. It can be estimated along with the solution of the CLE on each individual Brownian path, independently of the other paths.

Note that we are only interested in the sensitivity with respect to the reaction rate constants. The initial amounts of molecules are independent of the kinetic parameters, and thus the initial conditions for the sensitivities obey

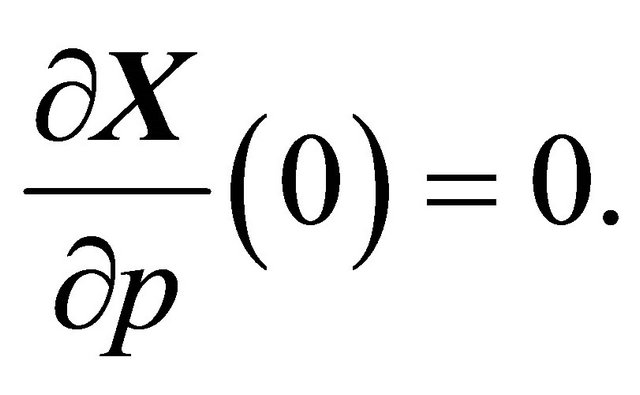(7)

In the following, this analysis will be used to reduce the complexity of the biochemical reaction system. Note that the parametric sensitivity presented here is accurate for choices of the kinetic parameters in some neighborhood of the values for which the analysis was applied, since our analysis focuses on estimating the local sensitivities.

4. A Model Reduction Strategy

We provide below a novel strategy for reducing the complexity of stochastic continuous models of wellstirred biochemical kinetics. The aim is to reduce the original model to a smaller one which preserves the dynamics, the stability properties and the physical relevance of the full system. This approach extends that of a parametric sensitivity for continuous deterministic systems, and in particular for the reaction rate equations [7].

Our method utilizes the pathwise (strong) sensitivity analysis for diffusive processes in the case of the Chemical Langevin Equation. Only the sensitivity with respect to the kinetic parameters is considered. The strategy will help identify the parameters having a strong influence of the system dynamics. The parameters which have an insignificant impact on the overall behavior the biochemical system, or on the species of interest, are then eliminated. Hence, their reactions are deleted, which leads also to the elimination of the unimportant species. This is particulary important, as the Chemical Langevin Equation model has as many equations as reacting species. Since the deleted species are constant in the reduced model, then the associated reduced CLE model becomes lower dimensional. These species are set to their initial value. Moreover, the Wiener processes associated with the deleted reactions are also removed, simplifying the numerical simulation and improving its efficiency.

For the Chemical Langevin model, the non-dimensional pathwise sensitivities depend on the particular Brownian path considered. Denote by 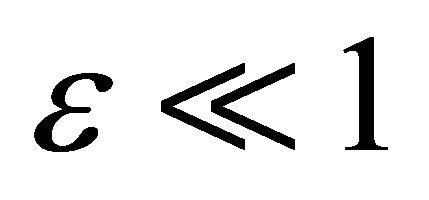the tolerance and by 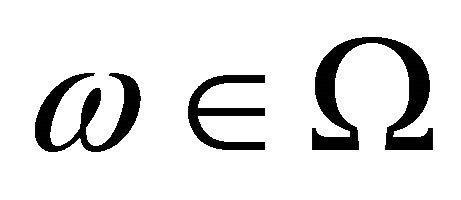a realization in the sample trajectory space. To estimate the pathwise sensitivity of 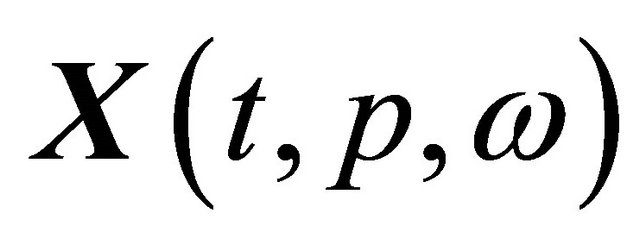with respect to the parameter , for a fixed sample trajectory, we integrate numerically the system (3) and (6), with the initial conditions (4) and (7) on that trajectory. Then, we impose the following strong criterion: the CLE system is robust (not sensitive) with respect to the parameter p if the non-dimensional (scaled) sensitivities satisfy

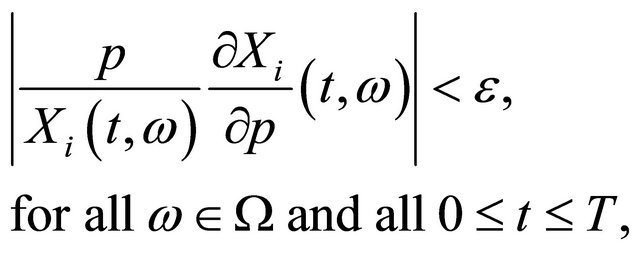(8)

for all 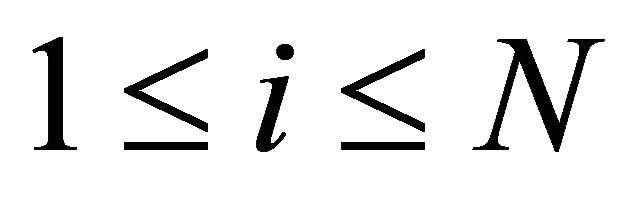or all species of interest. For the purpose of applying the sensitivity analysis to simplify stochastic continuous models of biochemical kinetics, this strong criterion may not be necessary.

We propose the following requirement for the elimination of the unimportant reactions, which is a weaker criterion than (8), but quite useful for simplifying biochemical kinetics. A reaction with reaction rate p may be eliminated, if for a given tolerance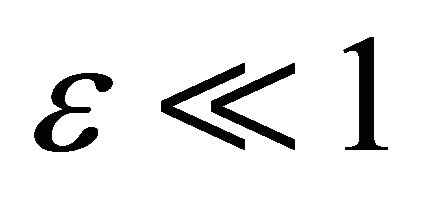, the sensitivities with respect to p obey

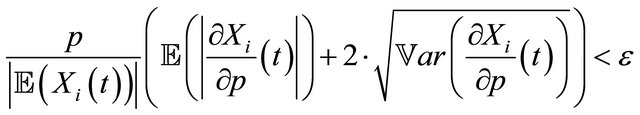(9)

for any 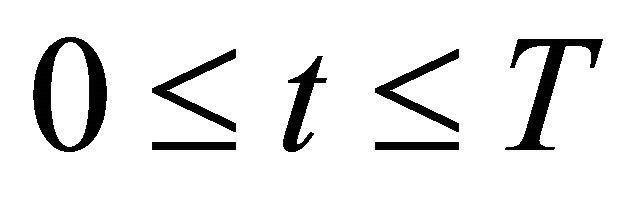and for all species of interest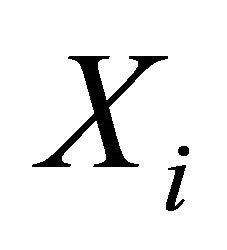. Here 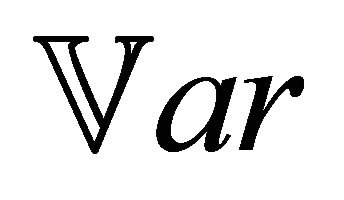denotes the variance.

5. Numerical Results

In this section, our strategy for simplifying the Chemical Langevin Equation model is tested on several examples of practical interest. In our tests, the Chemical Langevin Equation and the associated system of local sensitivities with respect to each kinetic parameter are integrated numerically. The underlying numerical method is the EulerMaruyama scheme. The reaction rates for which the associated sensitivities in the species of interest are very small, that is satisfy the requirement (9) for some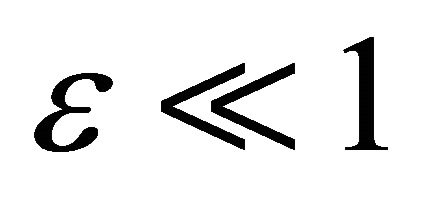, are identified. Then, the reactions corresponding to these kinetic parameters are eliminated. Finally, the relative errors in the mean and standard deviation of the reduced compared to the full system are estimated.

5.1. Modified Cycle Test Model

First, we study a modified cycle biochemical model [25], undergoing the following reaction channels

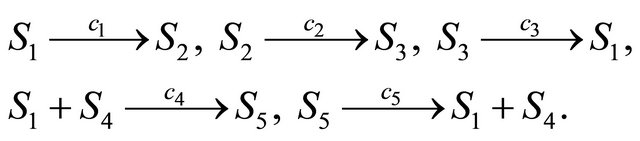
The state change vectors of this biochemical system are

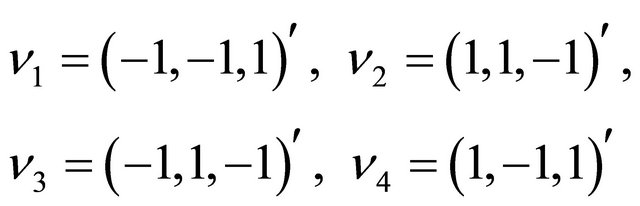
and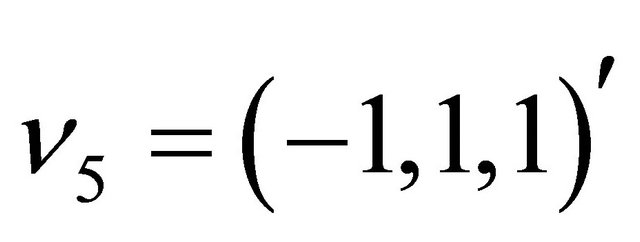. Furthermore, the reaction propensities are given by

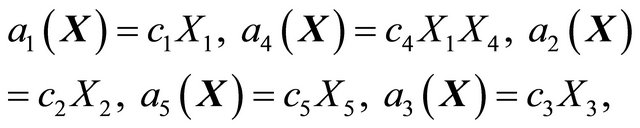
with the values of the kinetic parameters being

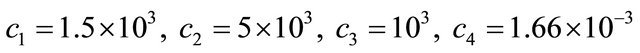
and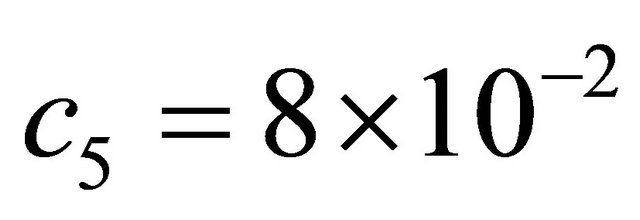. The model is integrated with initial conditions 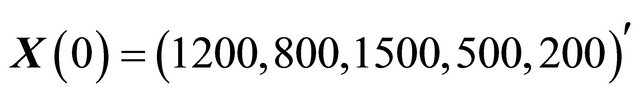on the time-interval [0, 10]. In our tests, the simulations are done over 10,000 trajectories.

We apply the pathwise sensitivity analysis to this model. The plots of the time-evolution of the sensitivities with respect to the species of interests, S1, S2 and S3, are presented in Figure 1. Notice that the non-dimensional sensitivities with respect to the parameters and of the species S1, S2 and S3 are very small, below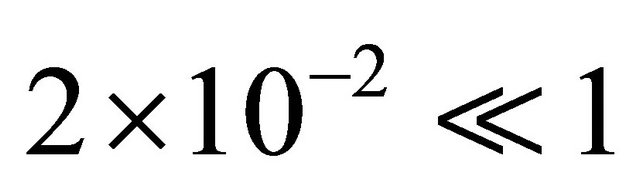, thus the system is robust with respect to

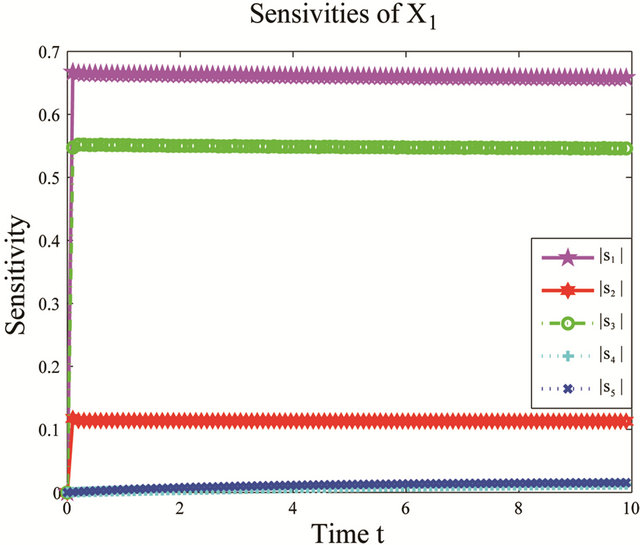
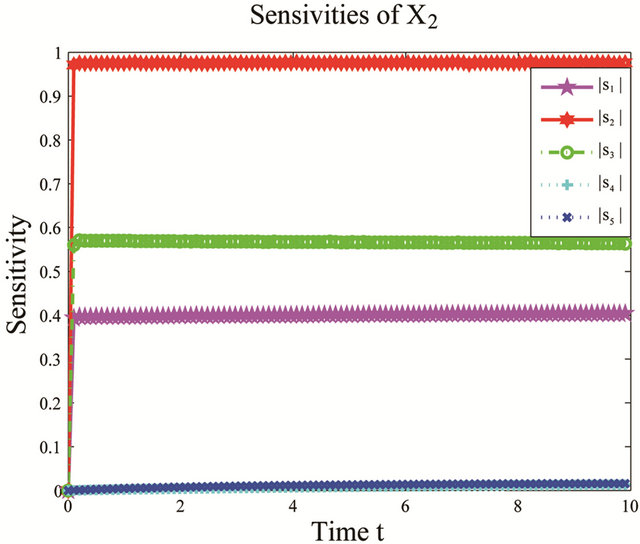
Figure 1. Sensitivity comparison for the cycle test model: the evolution in time of the sensitivities of X1, X2 and X3 with respect to the kinetic parameters, on the interval [0, 10]. The simulation uses 10,000 paths.

variations in these parameters. In addition, this shows that the reactions R4 and R5, together with the unimportant species S4 and S5, can be eliminated from the system, with a negligible effect on the dynamics of the important species, S1, S2 and S3. Figure 2 shows the graphs of the relative error, between the biochemical system without the reactions R4 and R5 and the full reaction system, for the mean and standard deviations in the species S1, S2 and S3. The relative errors in the mean are below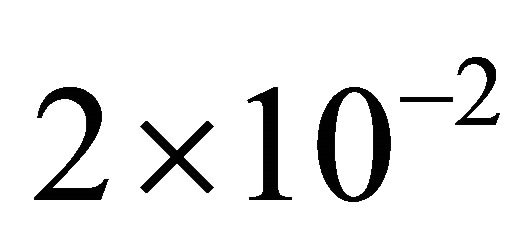, while the relative errors in the standard deviation are at most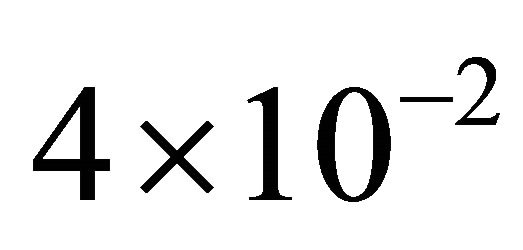. Consequently, the model reduction technique provided, based on pathwise sensitivity analysis, gives a very accurate representation of the statistical properties of interest for the biochemical system under consideration.

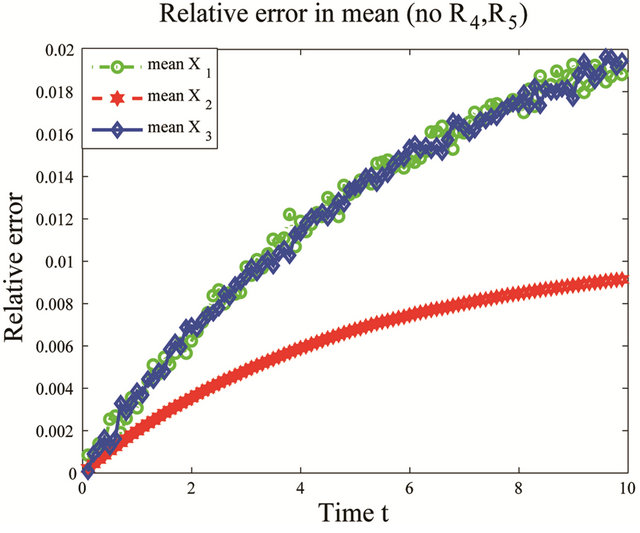
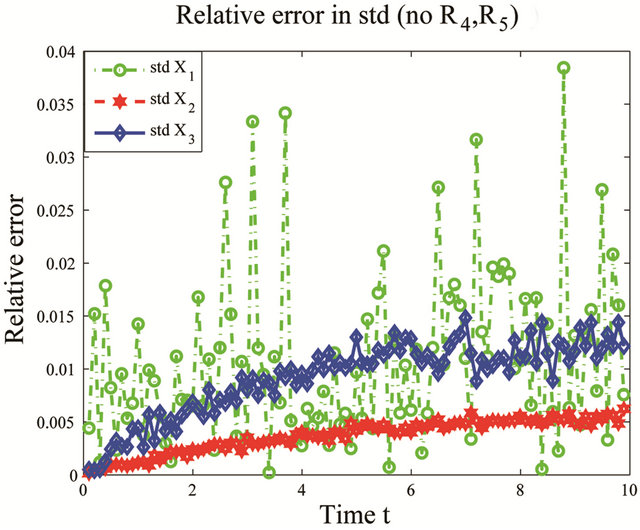
Figure 2. Cycle test model: the evolution in time of the relative errors in means (left) and std (right) of X1, X2 and X3 on the interval [0, 10], when the reactions R4 and R5 are eliminated, compared to the full system. The numerical simulations of the solution of the Chemical Langevin Equation used 10,000 trajectories.

5.2. Infectious Disease Model

Now, let us consider an infectious disease model [26] involving two components, the species S1 which caries the infectious disease and the species S2, which may become infected. The species are subject to the following reactions

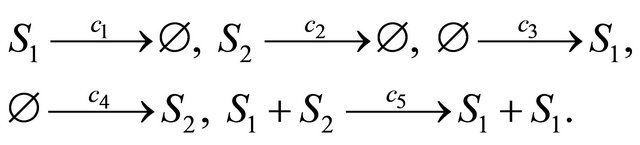
The reactions have state-change vectors given by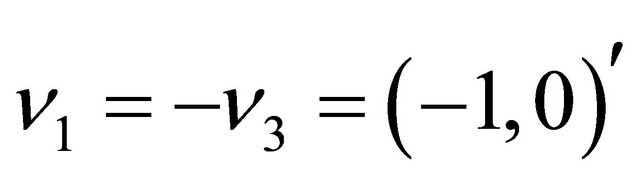, 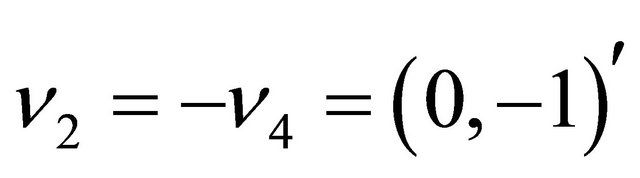and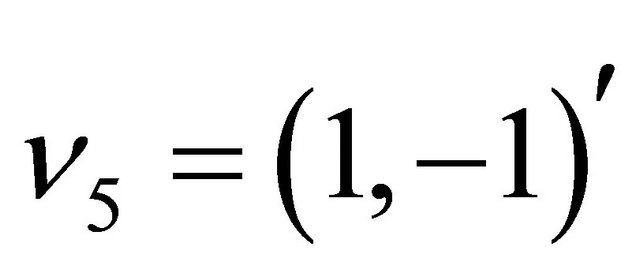. Each reactions is characterized by a propensity, expressed as

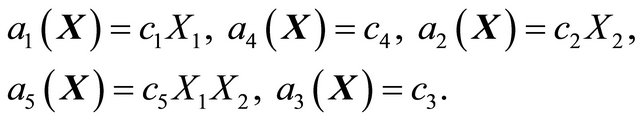
For this model, the kinetic parameters are 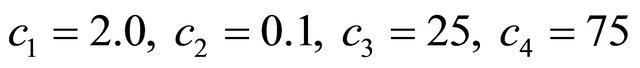and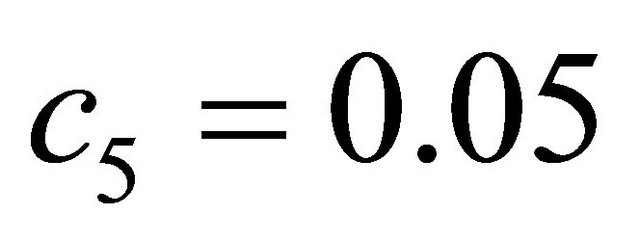. Integration is performed on the time interval [0, 10], with the initial conditions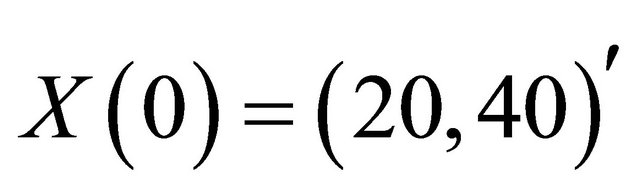. For our simulations, we approximate the exact solution of the Chemical Langevin Equation on 10,000 trajectories.

The pathwise sensitivity method for the Chemical Langevin Equation model is employed for this model. Figure 3 depicts the evolution of the non-dimensional sensitivities of the species S1 and S2 with respect to the kinetic parameters. Remark that the sensitivities with respect to c2 are quite small, less than 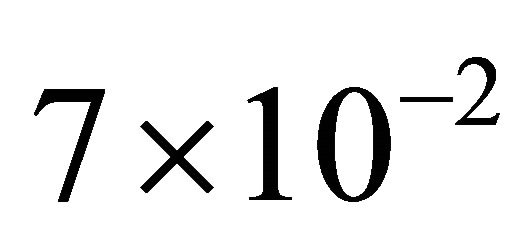for species S1 and S2. This indicates that the reaction R2 is unimportant, and thus can be deleted, with negligible influence on the overall behavior of the system. Figure 4 presents the evolution of the relative errors in the mean and standard deviation, between the reduced system (with the reaction R2 removed) and the full system, for the species S1 and S2, respectively. The relative errors are below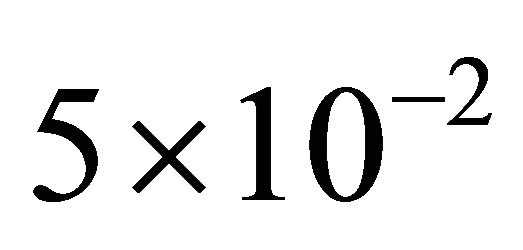, with the error in the mean being slightly larger than that in the standard deviation. We conclude that the model reduction techniques described above gives very good results on the infectious disease model with the set of parameters considered above.

5.3. A Multiscale Biochemical Model

Our final example is a biochemical model [27] undergoing the following reaction channels

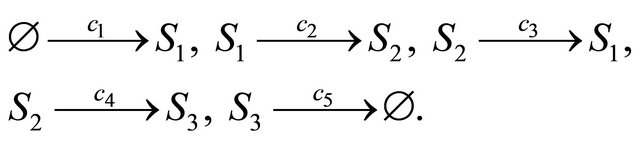
The propensities associated with the reactions above are

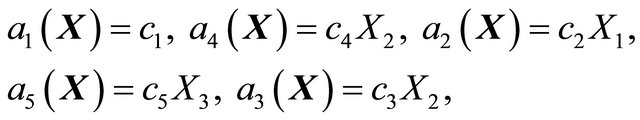
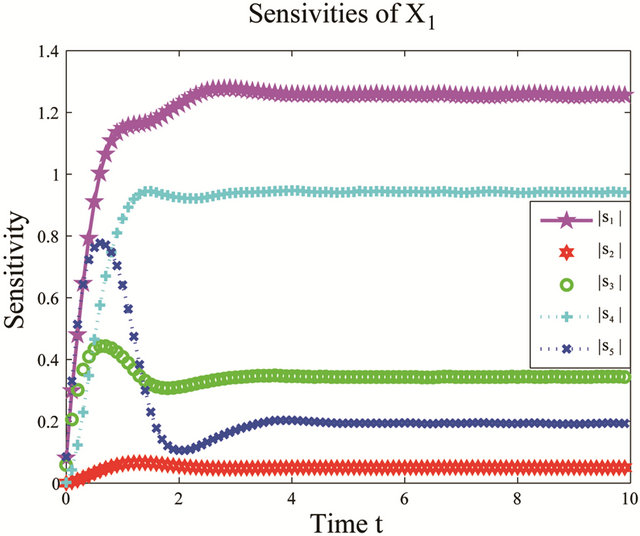
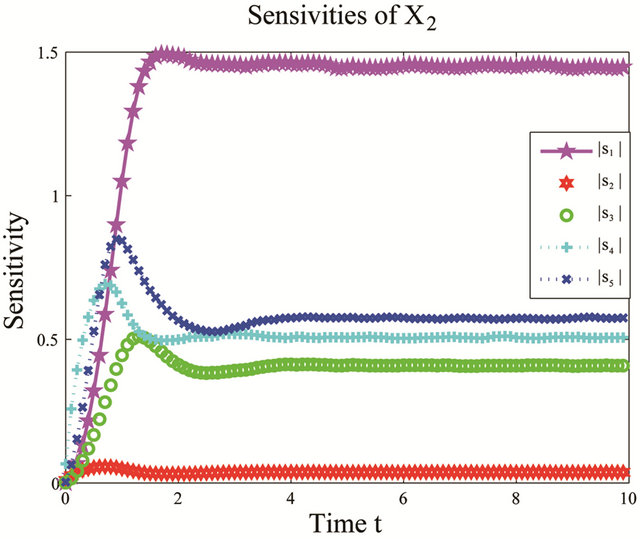
Figure 3. Sensitivity comparison for the infectious disease model: the evolution in time of the non-dimensional sensitivities of X1 and X2 with respect to the kinetic parameters, on the interval [0,10]. The simulations are over 10,000 trajectories.

while the state-change vectors are

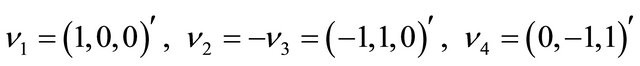
and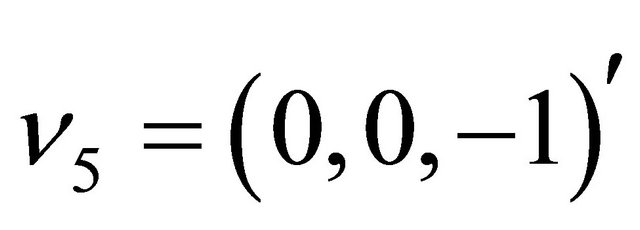. The kinetic parameters take the values 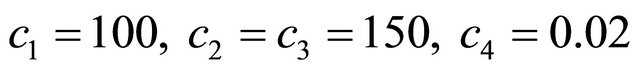and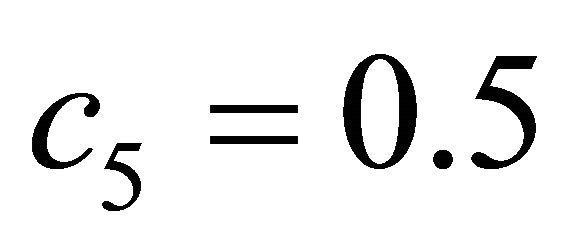. The system, integrated on the interval 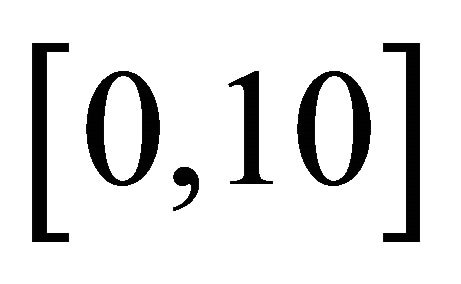with initial conditions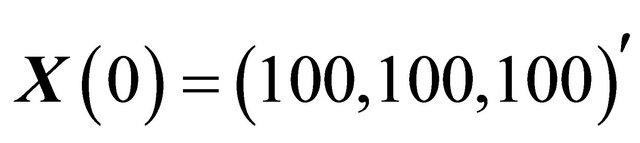, presents multiple scales in time.

We start by employing the sensitivity analysis method described above. The evolution of the non-dimensional sensitivities of the species of interest, S1 and S2, with respect to all parameters is depicted in Figure 5. Figure 5 shows that these species are robust with respect to variations in the parameters c4 and c5. Indeed, their sensitivities are below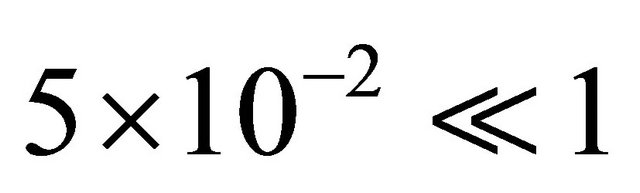. Thus, we can eliminate

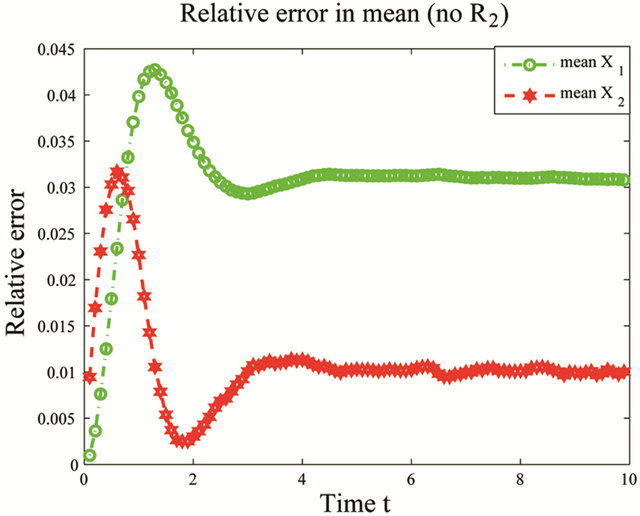
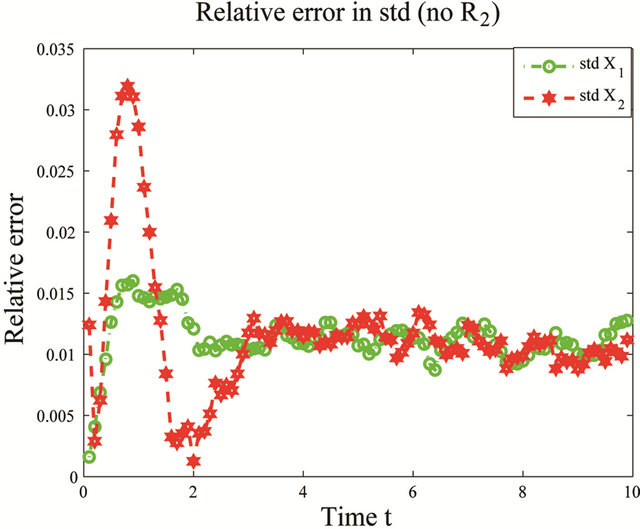
Figure 4. Infectious disease model: the evolution in time of the relative errors in mean and std of X1 and X2 in the interval [0,10], when the reaction R2 is eliminated, compared to the full system. The numerical solution of the Chemical Langevin Equation is computed on 10,000 trajectories.

the reactions R4 and R5 and the unimportant species X3. To estimate the changes in the important species dynamics, produced by the deletion of the unimportant reactions R4 and R5, we compute the relative error between the biochemical system with the reactions R4 and R5 removed and the full reaction system. The time-evolution of the relative errors in the mean and the standard deviation for the species of interest X1 and X2 is plotted in Figure 6. The relative errors in the mean for the species X1 and X2 are below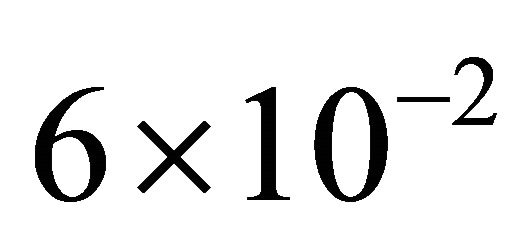, while the relative errors in the standard deviation are below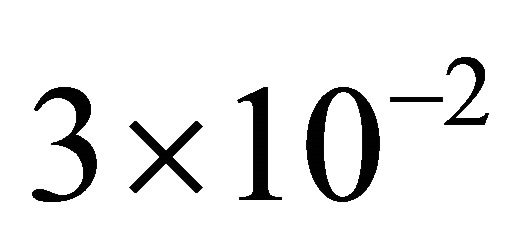. The CLE system was reduced from a model with 3 species subject to 5 reactions to a system of 2 species undergoing 3 reactions. We note that our model reduction strategy works very well for this biochemical model with multiple scales in time.

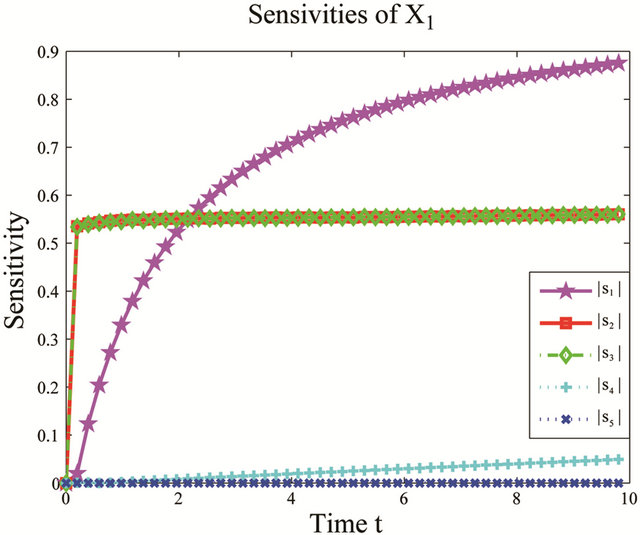
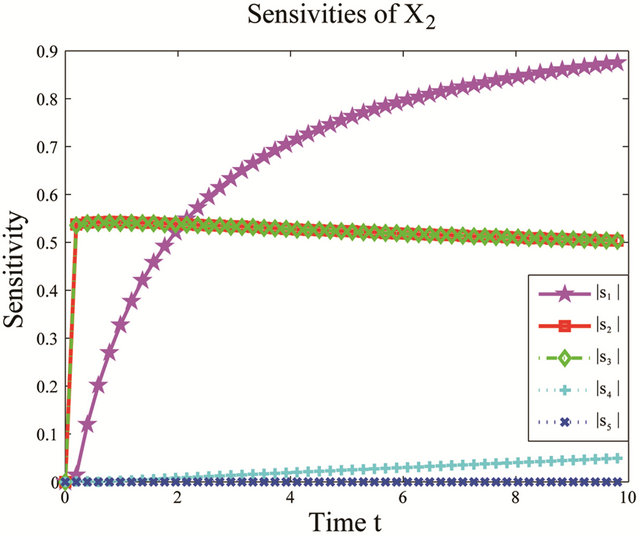
Figure 5. Sensitivity comparison for the multiscale biochemical model: the evolution in time of the non-dimensional sensitivities of X1 and X2 with respect to the kinetic parameters, on the interval [0,10]. The simulations are done on 10,000 trajectories.

6. Conclusion

In this paper, we developed a method to reduce biochemical systems modeled with the Chemical Langevin Equation. The Chemical Langevin Equation is a system of stochastic differential equations with multiplicative and non-commutative noise. Generally, the biochemical systems arising in applications are quite complex, involving many species and many reactions, and thus are difficult to simulate numerically and to analyze. The model reduction strategy provided utilizes the pathwise sensitivity analysis of stochastic differential equations to identify the parameters with an insignificant influence on the biochemical system dynamics. These parameters are eliminated together with the unimportant species, leading to a smaller model which maintains the characteristics of

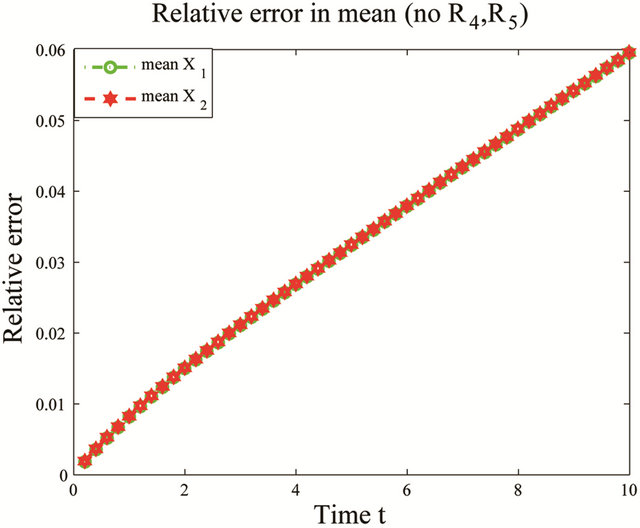
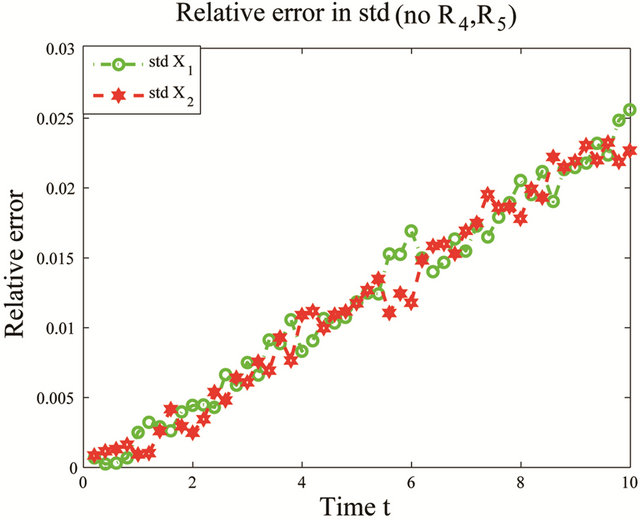
Figure 6. Multiscale biochemical model: the evolution in time of the relative errors in mean (left) and std (right) of X1 and X2 in the interval [0,10], when the reactions R4 and R5 are eliminated, compared to the full system. The solution of the Chemical Langevin Equation is approximated over 10,000 trajectories.

the full system, but is easier to analyze. The proposed model reduction technique has a simple implementation and may be used for a large class of biochemical reaction models, in the Langevin regime. We tested our method on several realistic models of biochemical kinetics and found an excellent agreement between the dynamics of the full and reduced models.

7. Acknowledgements

This research was supported by a grant from the Natural Sciences and Engineering Research Council of Canada (NSERC).

REFERENCES

  1. H. de Jong, “Modeling and Simulation of Genetic Regulatory Systems,” Journal of Computational Biology, Vol. 9, No. 1, 2002, pp. 67-103. doi:10.1089/10665270252833208
  2. M. B. Elowitz, A. J. Levine, E. D. Siggia and P. S. Swain, “Stochastic Gene Expression in a Single Cell,” Science, Vol. 297, No. 5584, 2002, pp. 1183-1186. doi:10.1126/science.1070919
  3. J. M. Raser and E. K. O’Shea, “Control of Stochasticity in Eukaryotic Gene Expression,” Science, Vol. 304, No. 5678, 2004, pp. 1811-1814. doi:10.1126/science.1098641
  4. D. J. Wilkinson, “Stochastic Modelling for Systems Biology,” Chapman & Hall/CRC, Leiden, 2006.
  5. S. Ilie and A. Teslya, “An Adaptive Stepsize Method for the Chemical Langevin Equation,” The Journal of Chemical Physics, Vol. 136, No. 18, 2012, pp. 184101- 184115. doi:10.1063/1.4711143
  6. M. S. Okino and M. L. Mavrovouniotis, “Simplification of Mathematical Models of Chemical Reactions,” Chemical Reviews, Vol. 98, No. 2, 1998, pp. 391-408. doi:10.1021/cr950223l
  7. L. R. Petzold and W. J. Zhu, “Model Reduction for Chemical Kinetics: An Optimization Approach,” AICHE Journal, Vol. 44, No. 4, 1999, pp. 869-886. doi:10.1002/aic.690450418
  8. H. Huang, M. Fairweather, J. F. Griffiths, A. S. Tomlin and R. B. Brad, “A Systematic Lumping Approach for the Reduction of Comprehensive Kinetic Models,” Proceedings of the Combustion Institute, Vol. 30, No.1, 2004, pp. 1309-1316. doi:10.1016/j.proci.2004.08.001
  9. G. Li and H. Rabitz, “A General Analysis of Exact Lumping in Chemical Kinetics,” Chemical Engineering Science, Vol. 44, No. 6, 1989, pp. 1413-1430.
  10. A. Kumar, P. D. Christofides and P. Daoutidis, “Singular Perturbation Modeling of Non-Linear Processes with Non-Explicit Time-Scale Separation,” Chemical Engineering Science, Vol. 53, No. 8, 1998, pp. 1491-1504. doi:10.1016/S0009-2509(98)00006-2
  11. N. Vora and P. Daoutidis, “Nonlinear Model Reduction of Chemical Reaction System,” AICHE Journal, Vol. 47, No. 10, 2001, pp. 2320-2332. doi:10.1002/aic.690471016
  12. Y. Cao, D. T. Gillespie and L. Petzold, “The Slow-Scale Stochastic Simulation Algorithm,” The Journal of Chemical Physics, Vol. 122, No. 1, 2005, pp. 014116-014134. doi:10.1063/1.1824902
  13. C. V. Rao and A. P. Arkin, “Stochastic Chemical Kinetics and the Quasi-Steady-State Assumption: Application to the Gillespie Algorithm,” The Journal of Chemical Physics, Vol. 118, No. 11, 2003, pp. 4999-5010. doi:10.1063/1.1545446
  14. A. Samant and D. Vlachos, “Overcoming Stiffness in Stochastic Simulation Stemming from Partial Equilibrium: A Multiscale Monte-Carlo Algorithm,” The Journal of Chemical Physics, Vol. 123, No. 14, 2005, pp. 144114- 144122. doi:10.1063/1.2046628
  15. D. T. Gillespie, “The Chemical Langevin Equations,” The Journal of Chemical Physics, Vol. 113, No. 1, 2000, pp. 297-306. doi:10.1063/1.481811
  16. D. T. Gillespie, “Exact Stochastic Simulation of Coupled Chemical Reactions,” The Journal of Physical Chemistry, Vol. 81, No. 25, 1977, pp. 2340-2361. doi:10.1021/j100540a008
  17. D. T. Gillespie, “A General Method for Numerically Simulating the Stochastic Time Evolution of Coupled Chemical Reactions”, The Journal of Computational Physics, Vol. 22, No. 4, 1976, pp. 403-434. doi:10.1016/0021-9991(76)90041-3
  18. D. T. Gillespie, “A Rigorous Derivation of the Chemical Master Equation,” Physica A, Vol. 188, No. 1-3, 1992, pp. 402-425. doi:10.1016/0378-4371(92)90283-V
  19. N. G. van Kampen, “Stochastic Processes in Physics and Chemistry,” Elsevier, Amsterdam, 2007.
  20. A. Varma, M. Morbidelli and H. Wu, “Parametric Sensitivity in Chemical Systems,” Cambridge University Press, Cambridge, 1999. doi:10.1017/CBO9780511721779
  21. M. Rathinam, P. W. Sheppard and M. Khammash, “Efficient Computation of Parameter Sensitivities of Discrete Stochastic Chemical Reaction Networks,” The Journal of Chemical Physics, Vol. 132, No. 3, 2010, pp. 034103- 034116. doi:10.1063/1.3280166
  22. P. W. Sheppard, M. Rathinam and M. Khammash, “A Pathwise Derivative Approach to the Computation of Parameter Sensitivities in Discrete Stochastic Chemical Systems,” The Journal of Chemical Physics, Vol. 136, No. 3, 2012, pp. 034115-034128. doi:10.1063/1.3677230
  23. Y. C. Ho and X. R. Cao, “Optimization and Perturbation Analysis and Queueing Networks,” Journal of Optimization Theory and Applications, Vol. 40, No. 4, 1983, pp. 559-582. doi:10.1007/BF00933971
  24. R. Suri and M. Zazanis, “Perturbation Analysis Gives Strongly Consistent Sensitivity Estimates for M/G/1 Queue,” Management Science, Vol. 34, No. 1, 1988, pp. 39-64. doi:10.1287/mnsc.34.1.39
  25. V. Sotiropoulos, M. N. Contou-Carrere, P. Daoutidis and Y. N. Kaznessis, “Model Reduction of Multiscale Chemical Langevin Equations: A Numerical Case Study,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, Vol. 6, No. 3, 2009, pp. 470-482. doi:10.1109/TCBB.2009.23
  26. T. Jahnke, “On Reduced Models for Chemical Master Equation,” Multiscale Modeling and Simulation, Vol. 9, No. 4, 2011, pp. 1646-1676.
  27. S. L. Cotter, K. C. Zygalakis, I. G. Kevrekidis and R. Erban, “A Constrained Approach to Multiscale Stochastic Simulation of Chemically Reacting Systems,” The Journal of Chemical Physics, Vol. 135, No. 9, 2011, pp. 094102-094114. doi:10.1063/1.3624333

NOTES

*Corresponding author.

Journal Menu >>