Applied Mathematics
Vol.3 No.8(2012), Article ID:21492,4 pages DOI:10.4236/am.2012.38133
The Theory of Vector-Valued Function in Locally Convex Space
Department of Mathematics, Dezhou University, Dezhou, China
Email: 735363648@qq.com
Received June 17, 2012; revised July 17, 2012; accepted July 24, 2012
Keywords: Locally Convex Space; Regular Function; Residue
ABSTRACT
In this paper, the vector-valued regular functions are extended to the locally convex space. The residues theory of the functions in the locally convex space is achieved. Thereby the Cauchy theory and Cauchy integral formula are extended to the locally convex space.
1. Introduction
The properties of analytic functions have been given in references [1,2]. The theory of analytic functions was extended to vector valued function in reference [3].
In this paper, we extended the theory of vector valued function to locally convex space.
Let 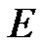 be a complete Hausdorff locally convex space on the real or complex domain
be a complete Hausdorff locally convex space on the real or complex domain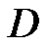 , and
, and  be the sufficient directed set of semi norms which generates the topology of
be the sufficient directed set of semi norms which generates the topology of . We denote the ad joint space of
. We denote the ad joint space of 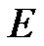 by
by , i.e.
, i.e. 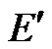 is the set of linear bounded functions on
is the set of linear bounded functions on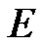 .
.
Definition 1 Let 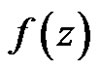 be a vector function defined on a domain
be a vector function defined on a domain 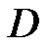 with values in
with values in . If there is an element
. If there is an element 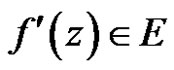 such that the difference quotient
such that the difference quotient
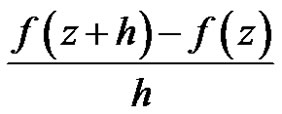 tends weakly(strongly) to
tends weakly(strongly) to  as
as
 , we call
, we call 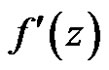 the weakly (strongly) derivative of
the weakly (strongly) derivative of 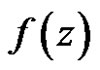 at
at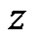 . We also say that
. We also say that 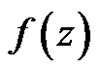 is weakly (strongly) derivative at
is weakly (strongly) derivative at 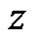 in
in . We call
. We call 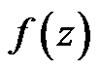 weakly (strongly) derivative in
weakly (strongly) derivative in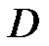 .
.
Definition 2 A vector function  is
is
1) weakly continuous at 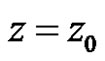 if
if
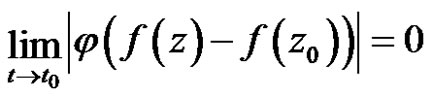 for each
for each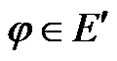 .
.
2) strongly continuous at  if
if
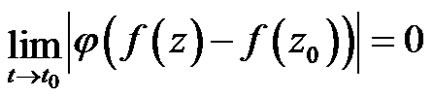 for each
for each .
.
Definition 3 A vector function 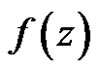 is said to be regular in
is said to be regular in 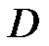 if
if 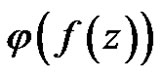 is regular for every
is regular for every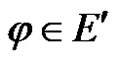 , where range of
, where range of 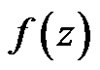 is in
is in . If a vector valued function
. If a vector valued function 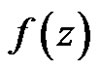 is regular in
is regular in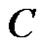 , then
, then 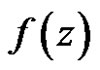 is called an entire function or said to be entire.
is called an entire function or said to be entire.
Theorem 1 [4] (Cauchy) If 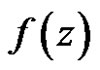 is a regular vector-valued function on the domain
is a regular vector-valued function on the domain 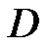 with values in the locally convex space
with values in the locally convex space . Let
. Let 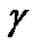 be a closed path in
be a closed path in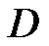 , and assume that
, and assume that 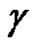 is homologous to zero in
is homologous to zero in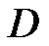 , then
, then
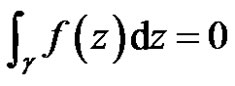
where c is a circle.
Proof For any linear bounded functional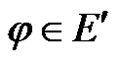 , we have
, we have
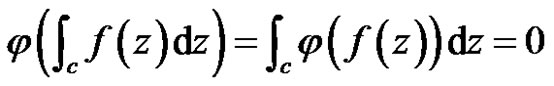 Hence
Hence
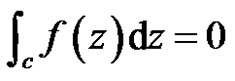
Theorem 2 [5] (Cauchy integral formula) Let 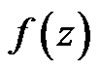 be a regular vector-valued function on the domain
be a regular vector-valued function on the domain 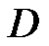 with values in the locally convex space
with values in the locally convex space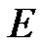 . Let
. Let 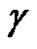 be a closed path in
be a closed path in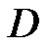 , and assume that
, and assume that 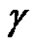 is homologous to zero in
is homologous to zero in , and let
, and let 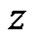 be in
be in 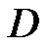 and not on
and not on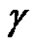 . Then
. Then
 (1)
(1)
where  is the index of the point
is the index of the point 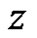 with respect to the curve
with respect to the curve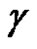 .
.
Proof For any linear bounded functional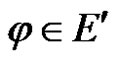 , we have
, we have
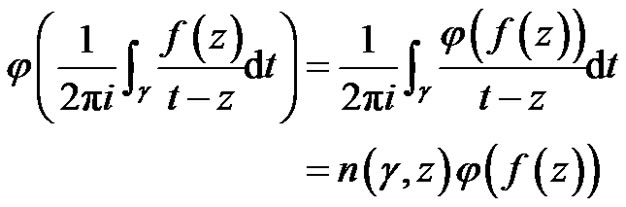 .
.
Then

2. The Main Conclusions
Theorem 3 Given the power series
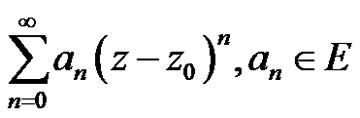 . (2)
. (2)
Set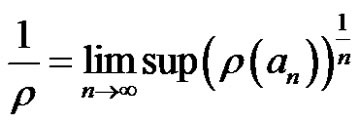 . Then the power series (2)
. Then the power series (2)
is absolutely convergent for 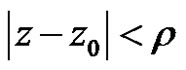 and divergent for
and divergent for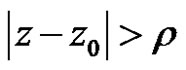 . The power series (2) convergence to a regular function on
. The power series (2) convergence to a regular function on 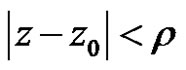 with values in
with values in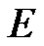 , the convergence being uniform in every circle of radius less than
, the convergence being uniform in every circle of radius less than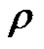 .
.
Proof First, we will prove the power series (2) is absolutely convergent for 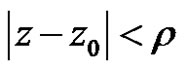 and divergent for
and divergent for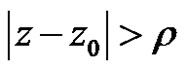 .
.
By Theorem 1, for any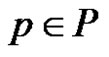 , we have
, we have
 where
where .
.
Let , then
, then
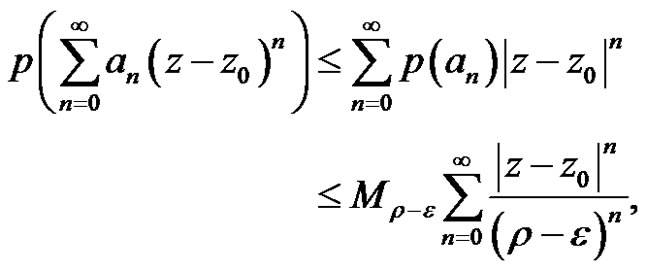
where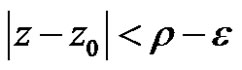 . Thus the power series (2) is absolutely convergence. But for
. Thus the power series (2) is absolutely convergence. But for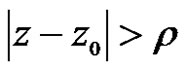 , if we suppose the power series (2) is convergence, it is contradict with the radius is
, if we suppose the power series (2) is convergence, it is contradict with the radius is . So the power series (2) is absolutely convergent for
. So the power series (2) is absolutely convergent for 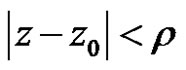 and divergent for
and divergent for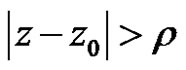 .
.
Secondly, for any linear bounded functional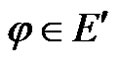 , we have
, we have
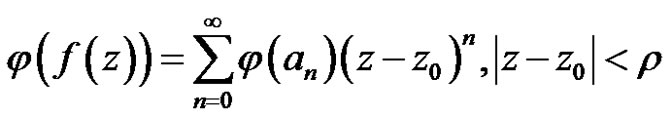 .
.
The right side series convergence to a regular function on 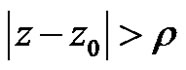 with values in
with values in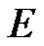 . So
. So 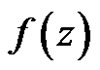 is regular in the circle and the convergence being uniform.
is regular in the circle and the convergence being uniform.
Definition 4 Let 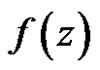 have an isolated singularity at
have an isolated singularity at  and let
and let
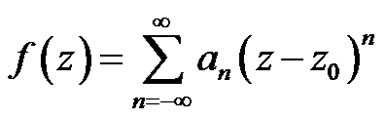 (3)
(3)
where
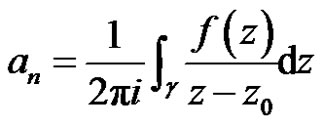 (4)
(4)
be its Laurent Expansions about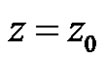 . The residue of
. The residue of 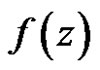 at
at 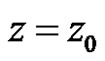 is the coefficient
is the coefficient . Denote this by
. Denote this by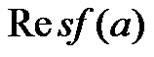 .
.
Theorem 4 Let 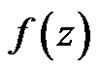 be a regular vector-valued function except for a finite number of points
be a regular vector-valued function except for a finite number of points  in the domain
in the domain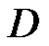 . Let
. Let 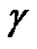 be a closed path in
be a closed path in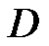 , and assume that
, and assume that 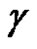 is homologous to zero in
is homologous to zero in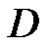 , and let
, and let 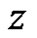 be in
be in 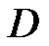 and not on
and not on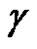 . Then
. Then
 (5)
(5)
Proof For any linear bounded functional , we have
, we have
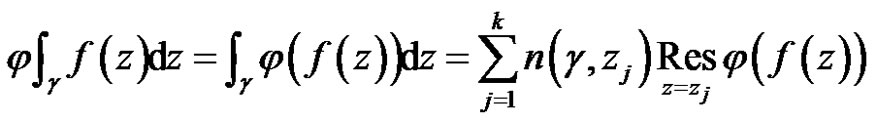 .
.
Then
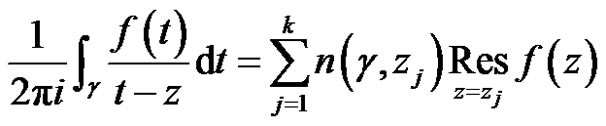
Theorem 5
1) If 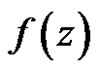 has a pole of order one at a point
has a pole of order one at a point 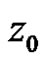
then
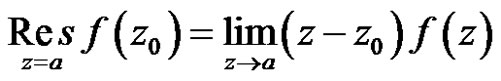 (6)
(6)
2) If 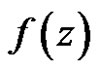 has a pole of order
has a pole of order ![]() at a point
at a point  then
then
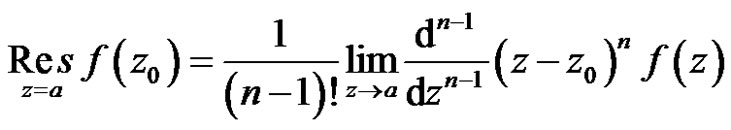 (7)
(7)
Proof Because  has a pole of order
has a pole of order ![]() at a point
at a point , then
, then  can be written in the form
can be written in the form
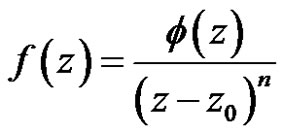
where 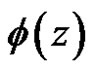 is regular and nonzero at
is regular and nonzero at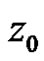 .
.
So 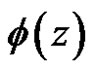 has a power series representation
has a power series representation

in some neighborhood of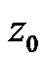 . It follows that
. It follows that
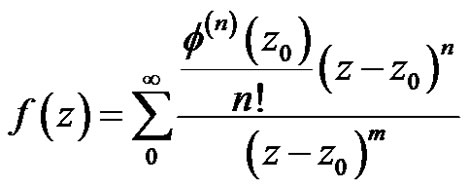
in some neighborhood of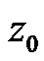 . Then we have formula (7)
. Then we have formula (7)
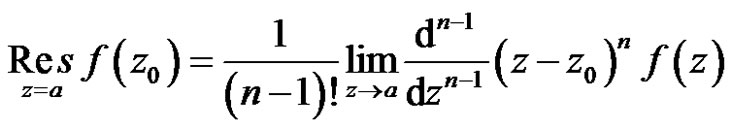
Obviously, when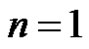 , the formula (7) is formula (6).
, the formula (7) is formula (6).
Theorem 6 If
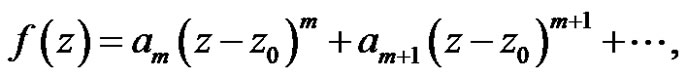
where 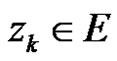 for
for 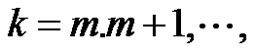 and if
and if 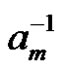 exists, then
exists, then 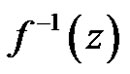 exist and has a pole with order
exist and has a pole with order ![]() at
at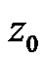 .
.
Proof Since
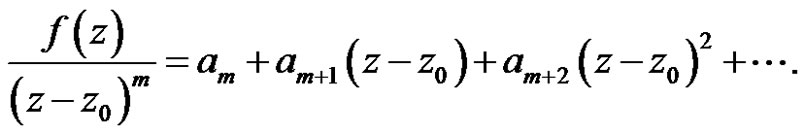
For any linear bounded functional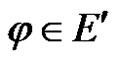 , we have
, we have
 as
as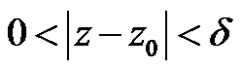 where
where ![]() is sufficiently small. Thus
is sufficiently small. Thus
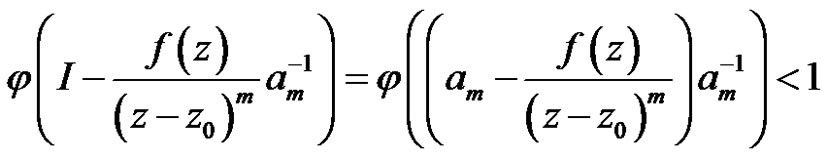 .
.
It follows that
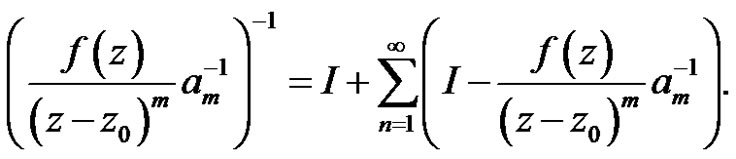
Therefore
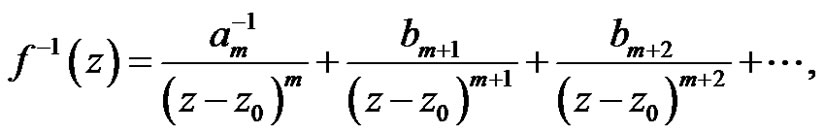
where 
Remark:  exist, this condition is important.
exist, this condition is important.
For example, in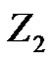 , we define
, we define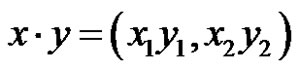 , where
, where 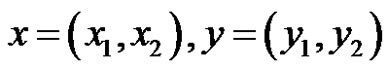 and For any linear bounded functional
and For any linear bounded functional 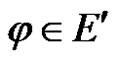
 .
.
Thus 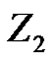 is a B-algebra, and
is a B-algebra, and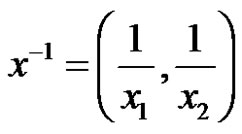 . We set
. We set
 where
where 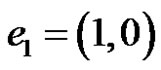 and
and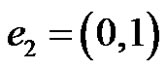 . It follows that
. It follows that 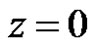 is zero with order one, but
is zero with order one, but
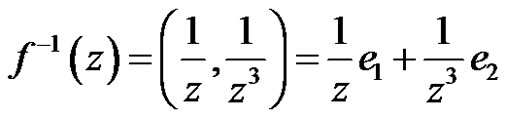
With order three.
Theorem 7 If 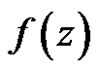 and
and 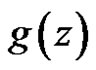 are regular in
are regular in 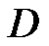 with values in
with values in 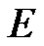 and if
and if ,
, 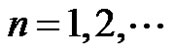 , the points
, the points 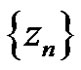 having a limit point in
having a limit point in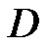 , then
, then 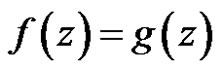 in
in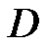 .
.
Proof For any linear bounded functional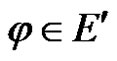 , we have
, we have
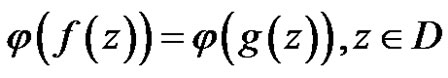
So
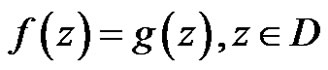 .
.
Theorem 8 Let  be defined in a domain
be defined in a domain 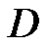 of the extended plane and on its boundary
of the extended plane and on its boundary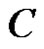 , regular in
, regular in 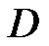 and strongly continuous in
and strongly continuous in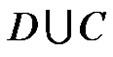 . If
. If
 then either
then either 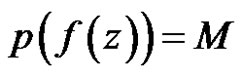 or
or  in
in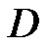 .
.
Proof For any linear bounded functional , we have
, we have
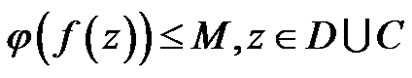 .
.
But except 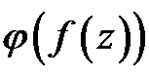 is constant,
is constant,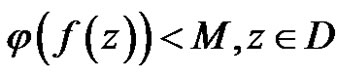 . So either
. So either 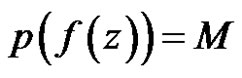 or
or 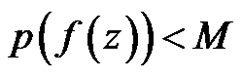 in
in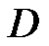 .
.
Remark: Unlike the classical case, 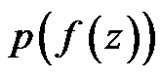 may have a minimum other zero in
may have a minimum other zero in 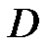 as the following example shows.
as the following example shows.
For example, Let 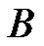 be a Banach space of complex pairs,
be a Banach space of complex pairs, 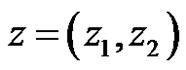 , where
, where .
.
Set
 Then
Then
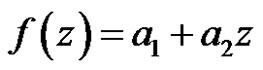 ,
, 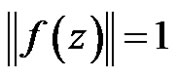 for
for 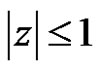
and
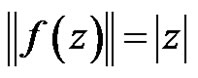 for
for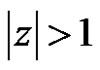 .
.
Theorem 9 If 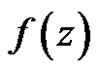 is regular in
is regular in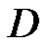 , and if
, and if 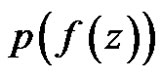 is bounded in
is bounded in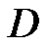 , then
, then 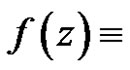 constant element.
constant element.
Proof For any linear bounded functional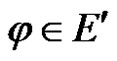 , we have
, we have
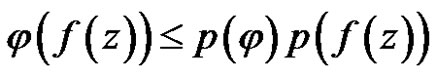 .
.
So  is bounded in
is bounded in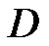 , then
, then 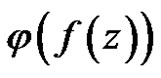 is constant.
is constant.
Suppose 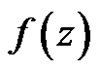 is not constant, then exist two point
is not constant, then exist two point 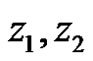 such that
such that
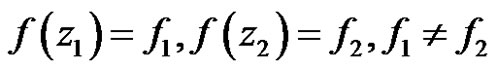 .
.
Thus exist  satisfy
satisfy
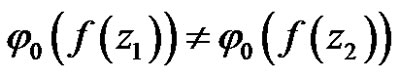 .
.
This is contradict with 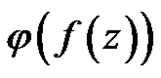 is constant. So
is constant. So 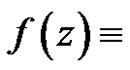 constant element.
constant element.
Theorem 10 If 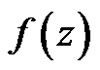 is regular in the unit circle, satisfy the condition
is regular in the unit circle, satisfy the condition 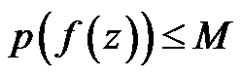 and
and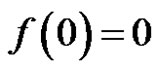 . Then
. Then
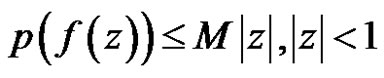 .
.
Proof For any linear bounded functional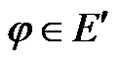 , we have
, we have
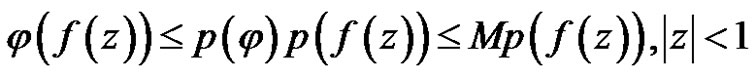 .
.
Since every point , their exist a bounded function
, their exist a bounded function ![]() such that
such that
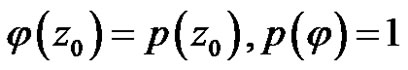 .
.
So
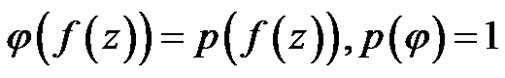 .
.
Then
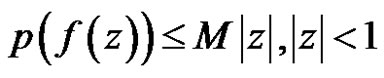 .
.
REFERENCES
- L. V. Ahlfors, “Complex Analysis,” McGraw-Hill, New York, 2004.
- S. Lang, “Complex Analysis,” Springer-Verlag, New York, 2003.
- C. G. Hu, “Vector-Valued Function and Its Applications,” Kluwer Academic Publishers, Dordrecht, Boston, London, 1992.
- C. P. Xie and Y. S. Zhao, “Basic Boundary Value Problem for Complex Harmonic Functions,” Beijing Math, Vol. 3, No. 1, 1997, pp. 20-35.
- Z. Zhen, “Schwarz’s Problems for Some Complex Partial Differential Equations of Second Order,” Beijing Math, Vol. 2, No. 1, 1996, pp. 131-137.

