Applied Mathematics
Vol. 3 No. 7 (2012) , Article ID: 19885 , 5 pages DOI:10.4236/am.2012.37112
An Approach for the Construction of Systems That Self-Generate Chaotic Solitons
Department of Applied Mathematics, Guangdong University of Technology, Guangzhou, China
Email: sunnycby@126.com
Received April 28, 2012; revised May 28, 2012; accepted June 5, 2012
Keywords: Chaotic Solitons; Partial Differential Equation; Homoclinic Orbit
ABSTRACT
This paper proposes a method for constructing partial differential equation (PDE) systems with chaotic solitons by using truncated normal forms of an ordinary differential equation (ODE). The construction is based mainly on the fact that the existence of a soliton in a PDE system is equal to that of a homoclinic orbit in a related ODE system, and that chaos of Ši’lnikov homoclinic type in the ODE imply that the soliton in the PDE changes its profile chaotically along propagation direction. It is guaranteed that the constructed systems can self-generate chaotic solitons without any external perturbation but with constrained wave velocities in a rigorously mathematical sense.
1. Introduction
Chaotic solitons have been a subject of many theoretical papers over the last decades of years. They have been experimentally observed in several physical systems [1- 4]. Despite this large amount of effort, many key issues remain open. The central question addressed in this paper is: How can one construct a partial differential equation (PDE) system that self-generates a chaotic solitary-wave pulse that exists in a rigorous sense? There are few rigorous results that addresses this question. In most cases, rigorous results for the generation of chaotic solitons are obtained through perturbations to a known system, e.g., Schrödinger equation and Ginzburg-Landau equation [5- 8], that can generate solitons. Unfortunately, this method is not regular since, in practice, it can be applied only to particular examples. Another rigorous approach is that of C. L. Zheng [9]. In this approach one must find variable separation solutions to a generalized (2 + 1)-dimensional Kotewege de-Vries equation by using Bäcklund transformations [10]. The approach can be in nature categorized to perturbation method. A third approach, by Wu et al. in [3] and Ricketts et al. in [4], is an experimental scheme. The former described a related system that deliberately provokes inherently nonlinear dynamics to produce chaotic soliton oscillations. The latter showed that the cancellation does more than simply allow the faithful propagation of digital pulses: in fact, it can be used as part of electrical oscillator to produce pulses in the first place. Both of these systems are purely electronic; their relative ease of manufacture gives them many advantages over the “photonic” devices, involving light waves, that currently dominate soliton research. As defined in [8], a chaotic soliton means that the soliton changes its profile chaotically in time or along propagation direction. From the view of mathematics, a soliton of a PDE system corresponds to a special solution of the PDE, or equally, a soliton corresponds to a homoclinic orbit in a related ordinary differential equation (ODE). Furthermore, if such an orbit is of Shilnikov’s type [11], that is, some Shilnikov’s inequalities are satisfied, then the ODE system definitely has chaos of Shilnikov’s type. It is not difficult to imagine that the corresponding soliton in the original PDE system should be a chaotic soliton since its profile impossibly behaves regularly in time. Such a relation between some solutions of ODE and PDE systems is the basis of our constructing PDE systems that self-generate chaotic solitons. On the other hand, from an ODE system with homoclinic orbits, one may construct many PDE systems such that they can self-generate solitons corresponding to the homoclinic orbits in the ODE system. Therefore, the construction must be treated carefully so that the resulting systems via the construction are as desired.
In this paper, we propose a method for constructing a PDE system self-generating chaotic solitons. The construction is based on the truncated normal forms of an autonomous ODE and on the relationship between ODEs and PDEs when solitary waves are under consideration. The constructed system can self-generate a chaotic solitary-wave pulse without any external perturbation. Moreover, the existence of the solitary-wave pulse in the PDE system is ensured by that of one homoclinic orbit of an ODE system whereas its chaotic behavior (i.e., the soliton changes its profile chaotically along propagation direction) results from the chaos property of the ODE system which is guaranteed by Ši’lnikov’s homoclinic theorem [11].
2. A Candidate Class of ODE Systems and Their Principle Homoclinic Orbits
Since finding a soliton in a PDE system can be changed into proving the existence of a homoclinic orbit in a related ODE system, in this section we will introduce a class of autonomous ODE systems as candidates for the construction of PDE systems that can self-generate chaotic solitons. The introduction of the candidate ODE systems is based on amplitude equations which are derived from normal form theory. Then, we discuss the existence of homoclinic orbits in the ODE systems. We do not prove the existence of the homoclinic orbit, and instead obtain some so-called principle homoclinic orbits by applying perturbation theory. Furthermore, we show that such homoclinic orbits are of Ši’lnikov’s type, implying that the ODE systems have chaos of Ši’lnikov’s type.
We begin by a general theory about the standard form of nonlinear ODE systems. In the analysis of the stability of static states of autonomous nonlinear ODE systems, linear theory produces normal modes that vary like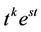 , where t is time, k is an integer, and
, where t is time, k is an integer, and 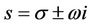 is a root of the characteristic value equation of the linear theory. Consider an autonomous nonlinear ODE system having a polycritical state in which
is a root of the characteristic value equation of the linear theory. Consider an autonomous nonlinear ODE system having a polycritical state in which 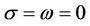 for l roots and
for l roots and 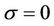 with
with  for m pairs of complex conjugate roots. Suppose that, for this state,
for m pairs of complex conjugate roots. Suppose that, for this state, 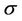 is bounded away from zero for all the other roots of the characteristic equation. By using normal form theory, we can obtain amplitude equations of the form:
is bounded away from zero for all the other roots of the characteristic equation. By using normal form theory, we can obtain amplitude equations of the form:
 (1)
(1)
where 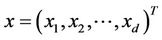 with
with 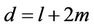 is the amplitude vector,
is the amplitude vector, 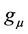 is a strictly nonlinear vector-valued function, and
is a strictly nonlinear vector-valued function, and 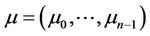 is a set of parameters. We restrict ourselves to cases where the number of parameters in the characteristic polynomial for
is a set of parameters. We restrict ourselves to cases where the number of parameters in the characteristic polynomial for 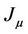 is equal to n (called criticality). In this case, the characteristic equation (called the critical polynomial) for matrix
is equal to n (called criticality). In this case, the characteristic equation (called the critical polynomial) for matrix 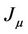 may be expressed as
may be expressed as
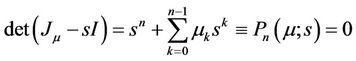 (2)
(2)
We are interested here in the leading-order terms in , e.g., for
, e.g., for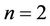 , they are of order
, they are of order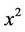 . These leading terms in
. These leading terms in 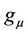 are dictated by
are dictated by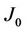 . For the critical condition,
. For the critical condition, 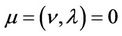 in the case of
in the case of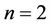 , the characteristic equation has zero as a double root. We refer to this case as
, the characteristic equation has zero as a double root. We refer to this case as  when
when  is an irreducible
is an irreducible 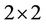 matrix. Similarly, we have other
matrix. Similarly, we have other 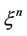 (see [12]). In addition, when
(see [12]). In addition, when 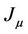 is in Jordan-Arnold form [12,13], we rewrite Equation (1) as
is in Jordan-Arnold form [12,13], we rewrite Equation (1) as
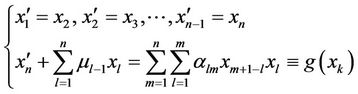 (3)
(3)
where the 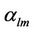 are constants which can be analytically calculated [14].
are constants which can be analytically calculated [14].
Let  be a small positive number and introduce the scaled variables
be a small positive number and introduce the scaled variables
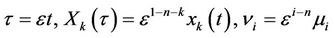 (4)
(4)
where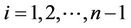 . If we arrange matters so that the
. If we arrange matters so that the 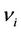 are of order unity, the values of
are of order unity, the values of  are near to the critical condition
are near to the critical condition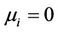 . That is, we position the system in that part of parameter space where, for
. That is, we position the system in that part of parameter space where, for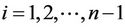 ,
,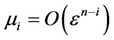 . Then Equation (3) becomes
. Then Equation (3) becomes
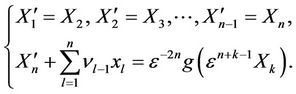 (5)
(5)
If we keep only the leading order terms in g, we may reduce Equation (5) to
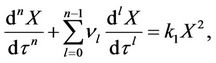 (6)
(6)
where 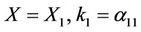 and we are ignoring terms
and we are ignoring terms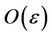 . Once we are within the region of parameter space delimited by
. Once we are within the region of parameter space delimited by , we may use Equation (6) as the amplitude equation for the configuration
, we may use Equation (6) as the amplitude equation for the configuration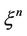 , for any n, with the error of order
, for any n, with the error of order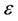 .
.
We are interested especially in the case of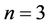 . In this case, we have the following truncated normal form as the amplitude equation for
. In this case, we have the following truncated normal form as the amplitude equation for 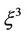 (see [13,14]):
(see [13,14]):
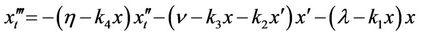 (7)
(7)
where 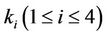 and
and 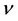 are constants. Equation (7) has two singular points
are constants. Equation (7) has two singular points  and
and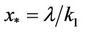 . We look for solutions of the form
. We look for solutions of the form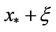 . If
. If 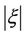 is small,
is small, 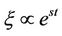 , and we obtain
, and we obtain
 (8)
(8)
The parameter 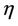 is a measure of the dissipation, and assumed to be positive. A change in the sign of
is a measure of the dissipation, and assumed to be positive. A change in the sign of 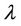 essentially interchanges the rules of the two singular points, so we need consider only
essentially interchanges the rules of the two singular points, so we need consider only . When
. When 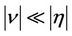 and
and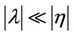 , we can obtain some principle homoclinic orbits by applying perturbation theory [12], e.g., for fixed
, we can obtain some principle homoclinic orbits by applying perturbation theory [12], e.g., for fixed , there is a principle homoclinic orbit for
, there is a principle homoclinic orbit for  when
when 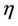 is small and the Ši’lnikov condition
is small and the Ši’lnikov condition 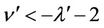 and
and  is satisfied with
is satisfied with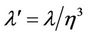 ,
,  (refer Figure 1). The region for existence of principle homoclinic orbits constitutes a cusp in shape, which is given by
(refer Figure 1). The region for existence of principle homoclinic orbits constitutes a cusp in shape, which is given by  and the cusp has a vertex at
and the cusp has a vertex at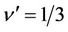 ,
, 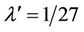 (see Figure 1). Besides these principle homoclinic orbits, there are many other homoclinic orbits in the problem (see [15]). Such a homoclinic orbit will imply the existence of chaos of Ši’lnikov type for an ODE system and ensure the existence of a chaotic soliton for a related PDE (see details in the next section).
(see Figure 1). Besides these principle homoclinic orbits, there are many other homoclinic orbits in the problem (see [15]). Such a homoclinic orbit will imply the existence of chaos of Ši’lnikov type for an ODE system and ensure the existence of a chaotic soliton for a related PDE (see details in the next section).
3. Constructing a PDE System That Self-Generates a Chaotic Soliton
A particular example is the asymptotic normal form for 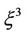 which is of the form:
which is of the form:
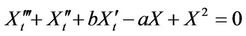 (9)
(9)
where X has been scaled to give a convenient coefficient to . Based on such an ODE and inspired by the relation between ODE and PDE when the travelling waves are considered, we construct the following model:
. Based on such an ODE and inspired by the relation between ODE and PDE when the travelling waves are considered, we construct the following model:
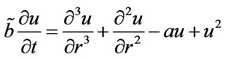 (10)
(10)
where a and 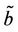 are positive constants. Assume that
are positive constants. Assume that

Figure 1. The principle homoclinic conditions for the case k1 = −1, k2 = k3 = 0, k4 = 1 of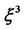 . The different curves are labelled by the values of
. The different curves are labelled by the values of 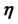 to which they correspond. The dotted curve corresponds to the location of the principle homoclinic orbit of the asymptotic form for
to which they correspond. The dotted curve corresponds to the location of the principle homoclinic orbit of the asymptotic form for 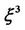 (see Equation (1)). Outside the cusp-shaped region R given by
(see Equation (1)). Outside the cusp-shaped region R given by![]() , the origin is a saddle-focus. To the right of the red curve marked by Sh, the Ši’lnikov condition
, the origin is a saddle-focus. To the right of the red curve marked by Sh, the Ši’lnikov condition 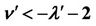 and
and 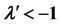 satisfied.
satisfied.
Equation (10) has travelling waves of the standard form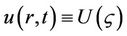 , where
, where 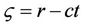 and c represents travelling wave speed (assume c > 0). Then, U satisfies Equation (9) with
and c represents travelling wave speed (assume c > 0). Then, U satisfies Equation (9) with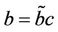 . Similarly, we can construct the classical Korteweg-de Vries (KdV) equation which has been applied to the optical fibers communication field if we set
. Similarly, we can construct the classical Korteweg-de Vries (KdV) equation which has been applied to the optical fibers communication field if we set ,
,  ,
, 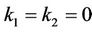 and
and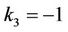 ,
, 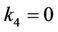 , based on the ODE (8). Now, we seek a solitary wave solution, that is, we find the solution of the following equation
, based on the ODE (8). Now, we seek a solitary wave solution, that is, we find the solution of the following equation 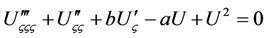 subjective to the constrain
subjective to the constrain 
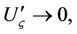
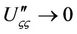 as
as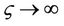 where the subscript stands for derivatives of function U with respect to the argument
where the subscript stands for derivatives of function U with respect to the argument . For this, we rewrite Equation (9) into an ODE
. For this, we rewrite Equation (9) into an ODE
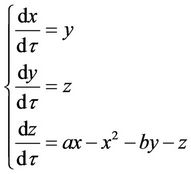 (11)
(11)
with the condition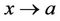 ,
, 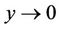 and
and 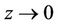 as
as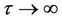 , where
, where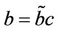 . Note that finding a soliton solution of Equation (10) satisfying the condition is currently changed into finding a homoclinic orbit of Equation (11) based at the equilibrium point
. Note that finding a soliton solution of Equation (10) satisfying the condition is currently changed into finding a homoclinic orbit of Equation (11) based at the equilibrium point .
.
Fourth-order Rounge-Kutta method is used to solve the system (11) with time step size equal to 0.01, the absolute and relative error equal to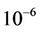 . Numerical simulation shows that the system (11) is chaotic when
. Numerical simulation shows that the system (11) is chaotic when 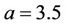 and
and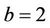 , as shown in Figure 2. Now, let us fix
, as shown in Figure 2. Now, let us fix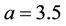 . The numerical simulation also shows that the existence interval of chaos reaches
. The numerical simulation also shows that the existence interval of chaos reaches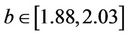 . Thus, we can determine the range of the solitary-wave velocity for fixed
. Thus, we can determine the range of the solitary-wave velocity for fixed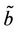 .
.
We can verify analytically that Equation (10) indeed has a Ši’lnikov homoclinic orbit and further chaos of Ši’lnikov type from a theorem of Ši’lnikov [11]. In fact, we have shown the existence of a homoclinic orbit (e.g., the principle homoclinic orbit) of Ši’lnikov type. Figure 3 shows the numerical soliton of Equation (10) according to the homoclinic orbit.
In addition, the characteristic polynomial of Jacobian matrix of Equation (10) evaluated at 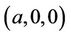 is
is 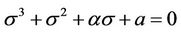 which has three roots: one negative
which has three roots: one negative 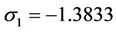 and a conjugate pair of complex
and a conjugate pair of complex 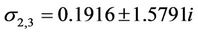 with the positive real part for
with the positive real part for 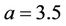 and
and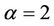 . A rigorously theoretical proof for the existence of chaos of Ši’lnikov type may be referred to a standard treatment in [16]. A chaotic soliton of Equation (10) with parameter
. A rigorously theoretical proof for the existence of chaos of Ši’lnikov type may be referred to a standard treatment in [16]. A chaotic soliton of Equation (10) with parameter 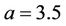 and
and 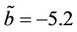 is shown in Figure 4 (the numerical simulation is performed for
is shown in Figure 4 (the numerical simulation is performed for  iterations with a time step of 0.001).
iterations with a time step of 0.001).
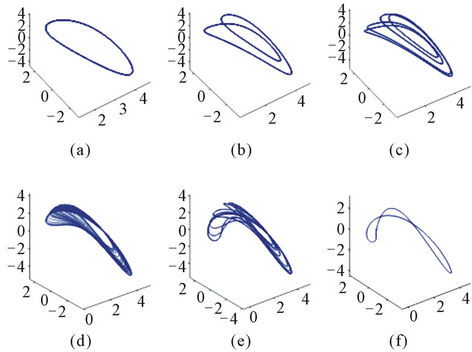
Figure 2. Evolution of the attractor of the asymptotic form for 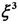 described by Equation (9) or (11) when the parameter b is (a) 2.5; (b) 2.1; (c) 2.05; (d) 2.0; (e) 1.88; (f) 1.419 for fixed a = 3.5. Here (a), (b), (c) illustrate the period-doubling cascade leading to the numerical strange attractor shown in (d) and (e). The principle homoclinic orbit is represented in (f): it is unstable. Transients are suppressed.
described by Equation (9) or (11) when the parameter b is (a) 2.5; (b) 2.1; (c) 2.05; (d) 2.0; (e) 1.88; (f) 1.419 for fixed a = 3.5. Here (a), (b), (c) illustrate the period-doubling cascade leading to the numerical strange attractor shown in (d) and (e). The principle homoclinic orbit is represented in (f): it is unstable. Transients are suppressed.
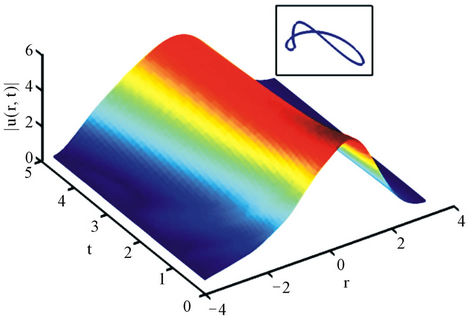
Figure 3. The numerical soliton, where parameter a = 3.5, 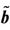 = −3.7.
= −3.7.
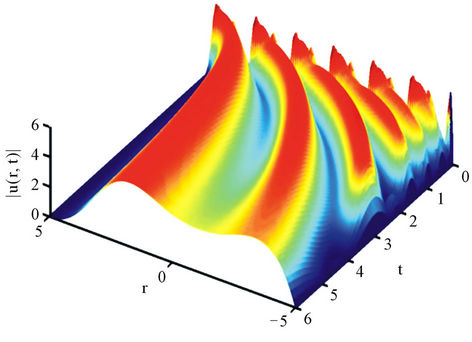
Figure 4. A numerical chaotic soliton, where parameter a = 3.5 and 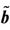 = −5.2.
= −5.2.
4. Conclusion
Based on normal form theory of ODEs, we have proposed a general method of constructing systems that selfgenerate chaotic solitons. By adjusting some system parameters in truncated normal forms of ODEs (e.g., Equation (8)), one can construct many systems with chaotic solitons. Note that the constructed system (10) is conservative. It seems the first example that self-generates chaotic solitons.
REFERENCES
- T. H. Lee, “Electrical Solitons Come of Age,” Nature, Vol. 440, 2006, pp. 36-37. doi:10.1038/440036a
- A. Argyris, et al., “Chaos-Based Communications at High Bit Rates Using Commercial Fibre-Optic Links,” Nature, Vol. 438, 2005, pp. 343-346. doi:10.1038/nature04275
- M. Z. Wu, B. A. Kalinikos and C. E. Patton, “Self-Generation of Chaotic Solitary Spin Wave Pulses in Magnetic Film Active Feedback Rings,” Physical Review Letters, Vol. 95, No. 23, 2005, 237202. doi:10.1103/PhysRevLett.95.237202
- D. S. Riketts, X. Li and D. Ham, “Electrical Soliton Oscillator,” IEEE Transactions on Microwave Theory and Techniques, Vol. 54, No. 1, 2006, pp. 373-382. doi:10.1109/TMTT.2005.861652
- S. V. Dmitriev, et al., “Chaotic Character of Two-Soliton Collisions in the Weakly Perturbed Nonlinear Schrö- dinger Equation,” Physical Review E, Vol. 66, No. 4, 2002, 046609. doi:10.1103/PhysRevE.66.046609
- S. V. Dmitriev and T. Shigenari, “Short-Lived TwoSoliton Bound States in Weakly Perturbed Nonlinear Schrödinger Equation,” Chaos, Vol. 12, No. 2, 2002, pp. 324-332. doi:10.1063/1.1476951
- F. Benvenuto, et al., “Manifestations of Classical and Quantum Chaos in Nonlinear Wave Propagation,” Physical Review A, Vol. 44, No. 6, 1991, R3423. doi:10.1103/PhysRevA.44.R3423
- N. Akhmediev, et al., “Pulsating Solitons, Chaotic Solitons, Period Doubling, and Pulse Coexistence in ModeLocking Lasers: Complex Ginzburg-Landau Equation Approach,” Physical Review E, Vol. 63, No. 5, 2001, Article ID: 056602. doi:10.1103/PhysRevE.63.056602
- C. L. Zheng, “Coherent Soliton Structures with Chaotic and Fractal Behaviors in a Generalized (2+1)-Dimensional Korteweg de-Vries System,” Chinese Journal of Physics, Vol. 41, 2003, pp. 442-456.
- S. P. Novikov and A. P. Veselov, “Two-Dimensional Schrödinger Operator: Inverse Scattering Transform and Evolutional Equations,” Physica D: Nonlinear Phenomena, Vol. 18, No. 1-3, 1986, pp. 267-273. doi:10.1016/0167-2789(86)90187-9
- F. C. P. Silva, “Ši'l'nikov Theorem—A Tutorial,” IEEE Transactions on Circuits and Systems, Vol. 40, 1993, pp. 675-682.
- V. I. Arnold, “Lectures in Bifurcation in Versal Families,” Russian Mathematical Surveys, Vol. 27, No. 5, 1972, pp. 54-123. doi:10.1070/RM1972v027n05ABEH001385
- A. Arneodo, et al., “Asymptotic Chaos,” Physica D: Nonlinear Phenomena, Vol. 14, No. 3, 1985, pp. 327-347. doi:10.1016/0167-2789(85)90093-4
- P. H. Coullet and E. A. Spiegel, “Amplitude Equations for Systems with Competing Instabilities,” SIAM Journal on Applied Mathematics, Vol. 43, No. 4, 1983, pp. 776- 821. doi:10.1137/0143052
- A. Arneodo, et al., “Oscillators with Chaotic Behavior: An Illustration of a Theorem by Shilnikov,” Journal of Statistical Physics, Vol. 27, 1982, pp. 171-182. doi:10.1007/BF01011745
- S. Wiggins, “Global Bifurcation and Chaos,” SpringerVerlag, New York, 1988. doi:10.1007/978-1-4612-1042-9

