Applied Mathematics
Vol. 3 No. 3 (2012) , Article ID: 18106 , 9 pages DOI:10.4236/am.2012.33042
Further Results on Pair Sum Graphs
1Department of Mathematics, Sri Paramakalyani College, Alwarkurichi, India
2Department of Mathematics, St. John’s College, Palayamcottai, India
3Department of Mathematics, Manonmaniam Sundaranar University, Tirunelveli, India
Email: ponrajmaths@indiatimes.com, parthi68@rediffmail.com, karthipyi91@yahoo.co.in
Received January 3, 2012; revised February 9, 2012; accepted February 16, 2012
Keywords: Path; Cycle; Ladder; Triangular Snake; Quadrilateral Snake
ABSTRACT
Let G be a  graph. An injective map
graph. An injective map  is called a pair sum labeling if the induced edge function,
is called a pair sum labeling if the induced edge function,  defined by
defined by  is one-one and
is one-one and 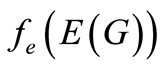 is either of the form
is either of the form 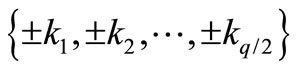 or
or  according as q is even or odd. A graph with a pair sum labeling is called a pair sum graph. In this paper we investigate the pair sum labeling behavior of subdivision of some standard graphs.
according as q is even or odd. A graph with a pair sum labeling is called a pair sum graph. In this paper we investigate the pair sum labeling behavior of subdivision of some standard graphs.
1. Introduction
The graphs considered here will be finite, undirected and simple. 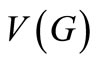 and
and 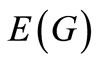 will denote the vertex set and edge set of a graph G. The cardinality of the vertex set of a graph G is denoted by p and the cardinality of its edge set is denoted by q. The corona
will denote the vertex set and edge set of a graph G. The cardinality of the vertex set of a graph G is denoted by p and the cardinality of its edge set is denoted by q. The corona 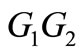 of two graphs
of two graphs 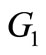 and
and 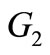 is defined as the graph obtained by taking one copy of
is defined as the graph obtained by taking one copy of  (with
(with 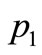 vertices) and
vertices) and 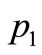 copies of
copies of 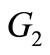 and then joining the ith vertex of
and then joining the ith vertex of 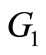 to all the vertices in the ith copy of
to all the vertices in the ith copy of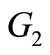 . If e = uv is an edge of G and w is a vertex not in G then e is said to be subdivided when it is replaced by the edges uw and wv. The graph obtained by subdividing each edge of a graph G is called the subdivision graph of G and it is denoted by
. If e = uv is an edge of G and w is a vertex not in G then e is said to be subdivided when it is replaced by the edges uw and wv. The graph obtained by subdividing each edge of a graph G is called the subdivision graph of G and it is denoted by . The graph
. The graph 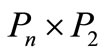 is called the ladder. A dragon is a graph formed by joining an end vertex of a path
is called the ladder. A dragon is a graph formed by joining an end vertex of a path 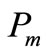 to a vertex of the cycle
to a vertex of the cycle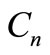 . It is denoted as
. It is denoted as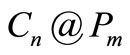 . The triangular snake
. The triangular snake 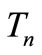 is obtained from the path
is obtained from the path  by replacing every edge of a path by a triangle
by replacing every edge of a path by a triangle . The quadrilateral snake
. The quadrilateral snake 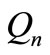 is obtained from the path
is obtained from the path 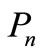 by every edge of a path is replaced by a cycle
by every edge of a path is replaced by a cycle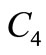 . The concept of pair sum labeling has been introduced in [1]. The Pair sum labeling behavior of some standard graphs like complete graph, cycle, path, bistar, and some more standard graphs are investigated in [1-3]. That all the trees of order ≤9 are pair sum have been proved in [4]. Terms not defined here are used in the sense of Harary [5]. Let x be any real number. Then
. The concept of pair sum labeling has been introduced in [1]. The Pair sum labeling behavior of some standard graphs like complete graph, cycle, path, bistar, and some more standard graphs are investigated in [1-3]. That all the trees of order ≤9 are pair sum have been proved in [4]. Terms not defined here are used in the sense of Harary [5]. Let x be any real number. Then 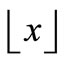 stands for the largest integer less than or equal to x and
stands for the largest integer less than or equal to x and  stands for the smallest integer greater than or equal to x. Here we investigate the pair sum labeling behavior of
stands for the smallest integer greater than or equal to x. Here we investigate the pair sum labeling behavior of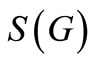 , for some standard graphs G.
, for some standard graphs G.
2. Pair Sum Labeling
Definition 2.1. Let G be a 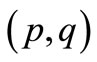 graph. An injective map
graph. An injective map  is called a pair sum labeling if the induced edge function,
is called a pair sum labeling if the induced edge function, 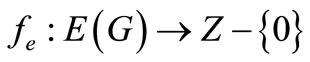 defined by
defined by 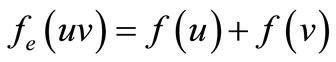 is one-one and
is one-one and 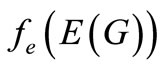 is either of the form
is either of the form
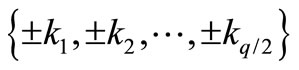
or
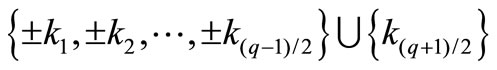
according as q is even or odd. A graph with a pair sum labeling defined on it is called a pair sum graph.
Theorem 2.2 [1]. Any path is a pair sum graph.
Theorem 2.3 [1]. Any cycle is a pair sum graph.
3. On Standard Graphs
Here we investigate pair sum labeling behavior of 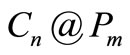 and
and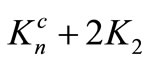 .
.
Theorem 3.1. If n is even, 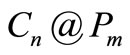 is a pair sum graph.
is a pair sum graph.
Proof. Let 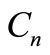 be the cycle
be the cycle 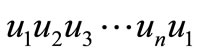 and let
and let 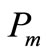 be the path
be the path .
.
Case 1. 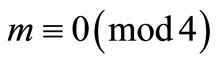
Define
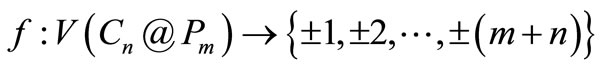
by
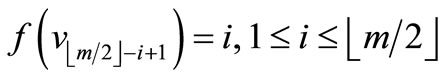
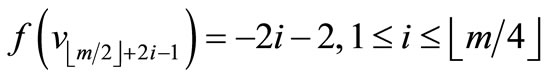
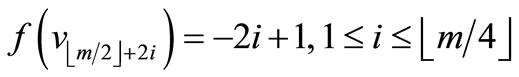

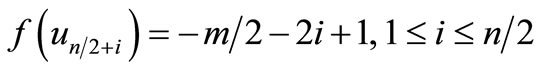 .
.
Here
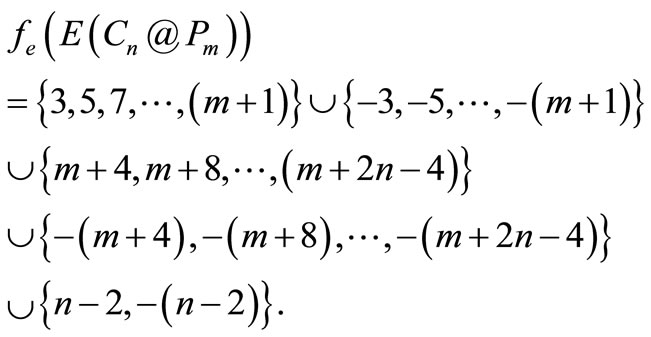
Therefore f is a pair sum labeling.
Case 2. 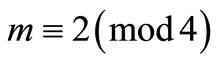
Define
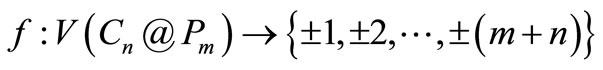
by
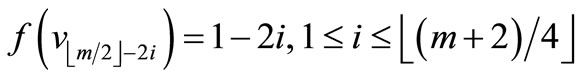
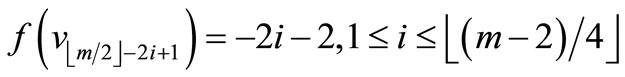
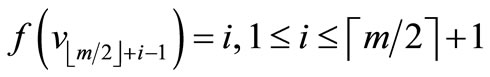
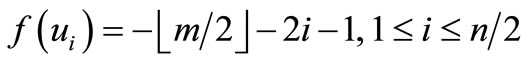

Here
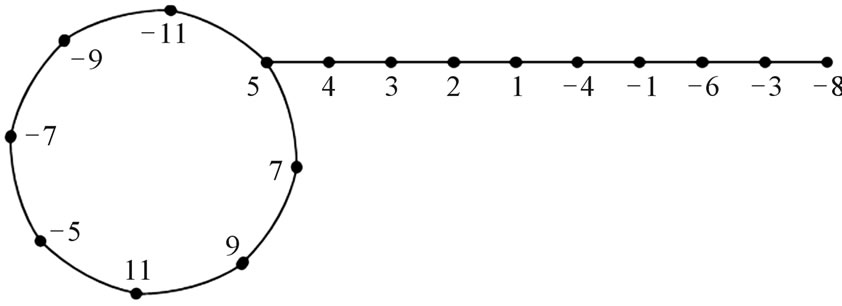
Figure 1. A pair sum labeling of .
.
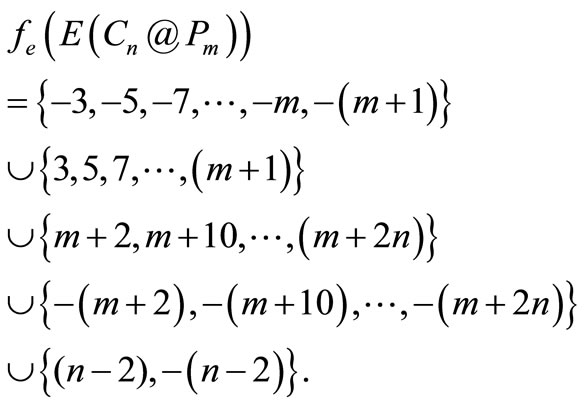
Hence f is a pair sum labeling.
Case 3. 
Label the vertex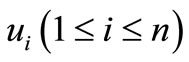 ,
, 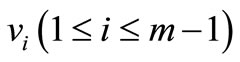 as in Case 1. Then label
as in Case 1. Then label 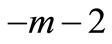 to
to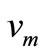 .
.
Case 4. 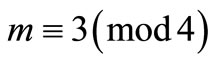
Assign the label 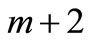 to
to 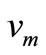 and assign the label to the remaining vertices as in Case 2.
and assign the label to the remaining vertices as in Case 2.
Illustration 1. A pair sum labeling of  is shown in Figure 1.
is shown in Figure 1.
Theorem 3.2. 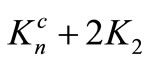 is pair sum graph if n is even.
is pair sum graph if n is even.
Proof: Let 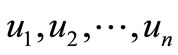 be the vertices of
be the vertices of  and u, v, w, z. be the vertices in
and u, v, w, z. be the vertices in 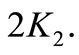 Let
Let
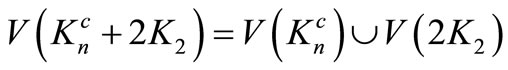
and

Define
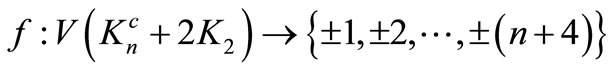
by
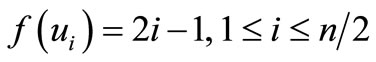

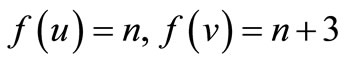
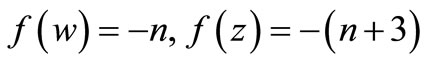
Here

Therefore f is a pair sum labeling.
Illustration 2. A pair sum labeling of 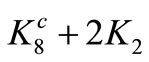
 is shown in Figure 2.
is shown in Figure 2.
4. On Subdivision Graph
Here we investigate the pair sum labeling behavior of 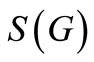 for some standard graphs G.
for some standard graphs G.
Theorem 4.1. 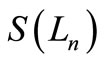 is a pair sum graph, where
is a pair sum graph, where 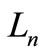 is a ladder on n vertices.
is a ladder on n vertices.
Proof. Let
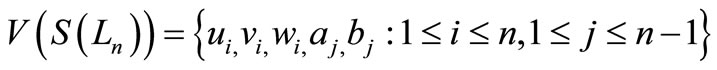
Let
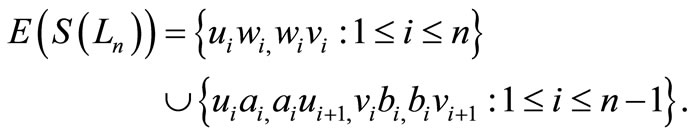
Case 1: n is even.
When n = 2, the proof follows from the Theorem 2.3. For n > 2Define
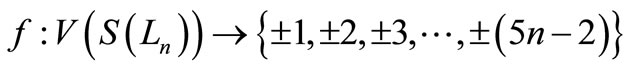
by
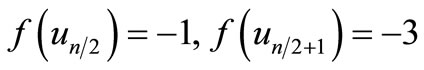
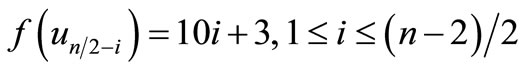
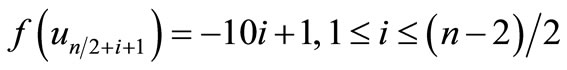
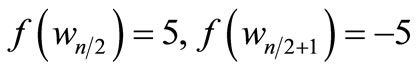
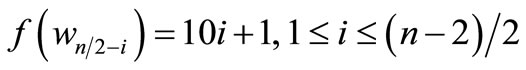

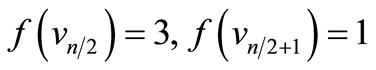

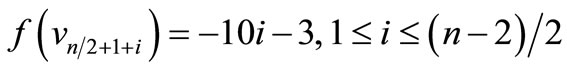
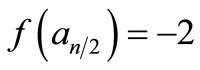
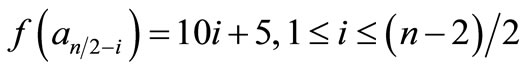
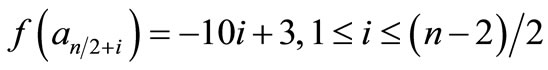
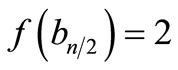
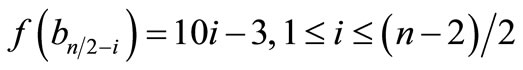
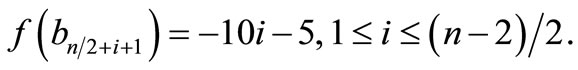
When n = 4,

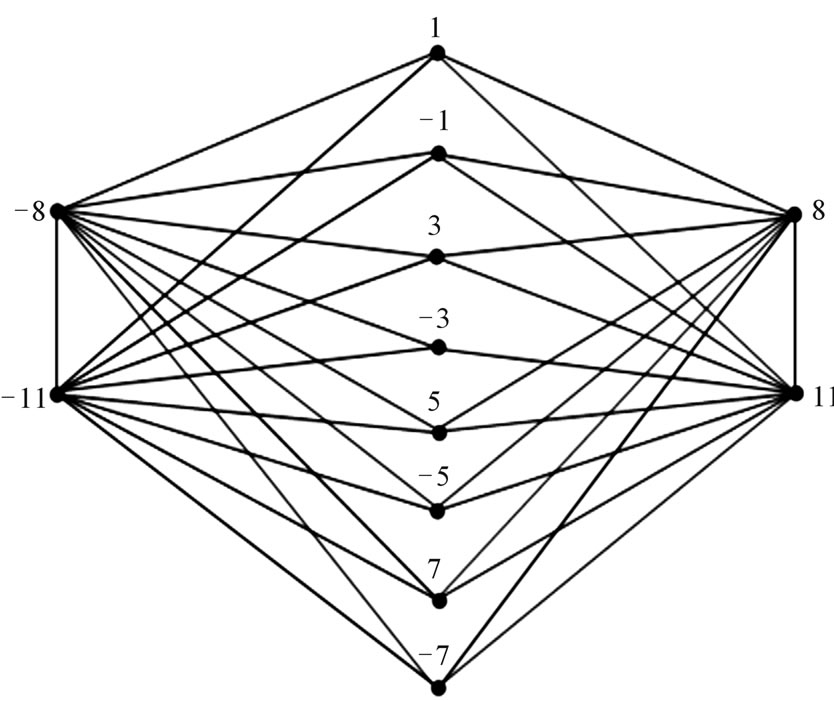
Figure 2. A pair sum labeling of .
.
For n > 4,

Therefore f is a pair sum labeling.
Case 2. n is odd.
Clearly  and hence
and hence  is a pair sum graph by Theorem 2.2. For n > 1Define
is a pair sum graph by Theorem 2.2. For n > 1Define
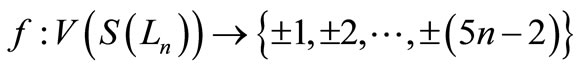
by
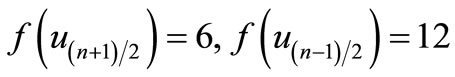
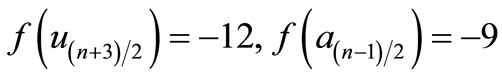

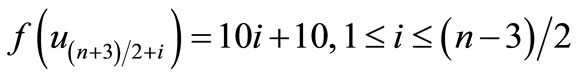
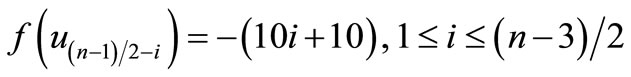
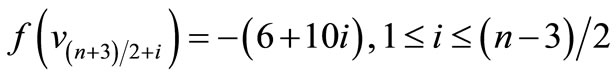


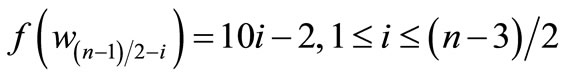
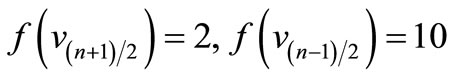
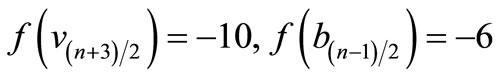
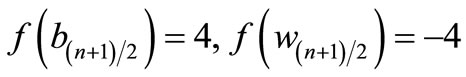
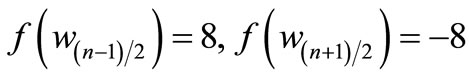
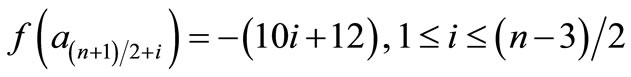
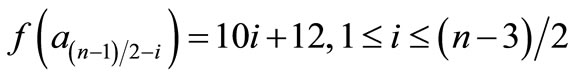

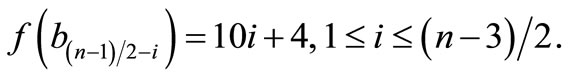
Therefore
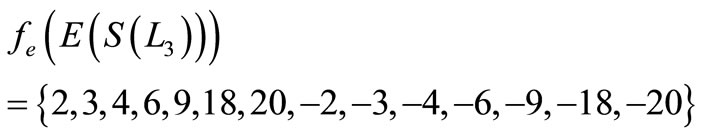
and
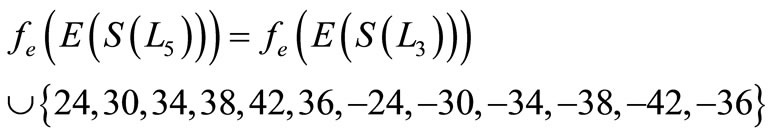
when n > 5,

Then f is a pair sum labeling.
Illustration 3. A pair sum labeling of 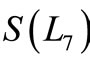 is shown in Figure 3.
is shown in Figure 3.
Theorem 4.2. 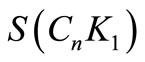 is a pair sum graph Proof. Let
is a pair sum graph Proof. Let
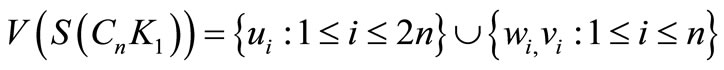

Figure 3. A pair sum labeling of .
.
Let
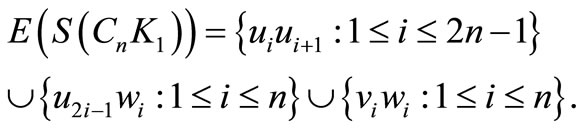
Case 1. n is even.
Define

by

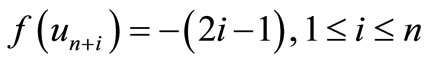

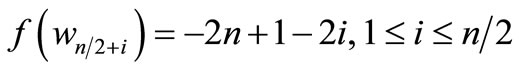
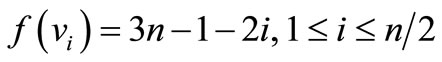
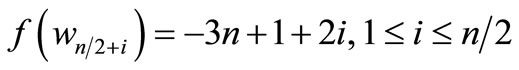
Here

Then f is pair sum labeling.
Case 2. n is odd.
Define
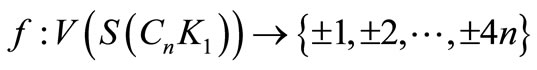
by
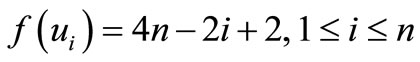


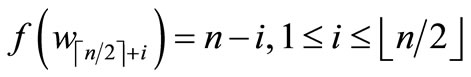

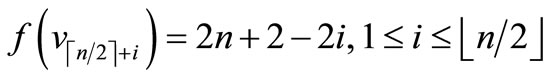
Here
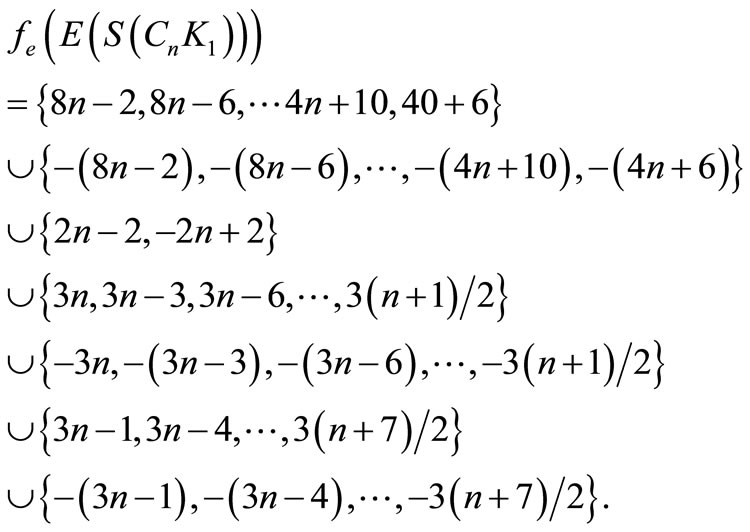
Then f is pair sum labeling.
Illustration 4. A pair sum labeling of  is shown in Figure 4.
is shown in Figure 4.

Figure 4. A pair sum labeling of .
.
Theorem 4.3. 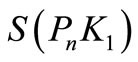 is a pair sum graph.
is a pair sum graph.
Proof. Let
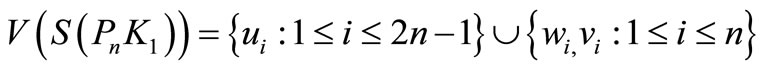
Let
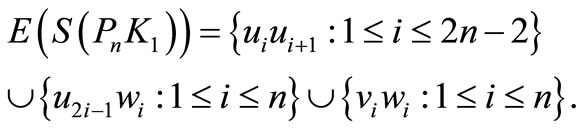
Case 1. n is even.
When n = 2, the proof follows from Theorem 2.2. For n > 2, Define
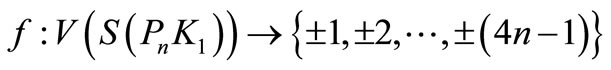
by
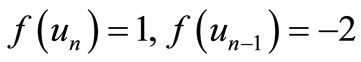
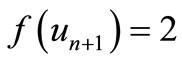
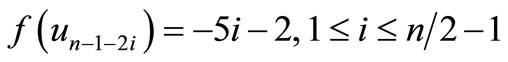
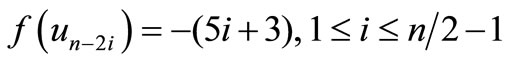
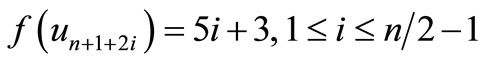
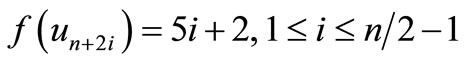
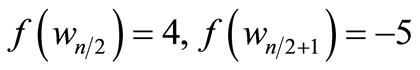
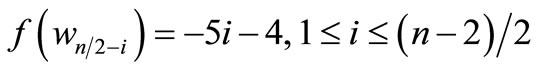
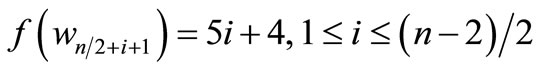
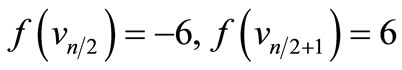


Here

For n > 4,
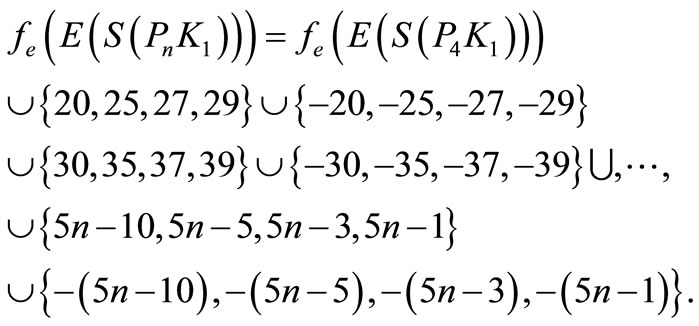
Then f is pair sum labeling.
Case 2. n is odd.
Since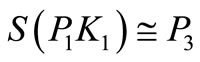 , which is a pair sum graph by Theorem 2.3. For n > 1, Define
, which is a pair sum graph by Theorem 2.3. For n > 1, Define

by
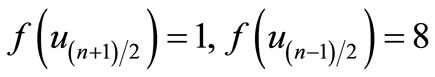
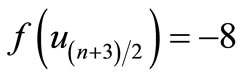
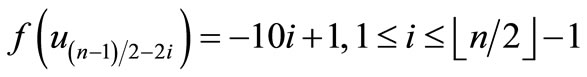

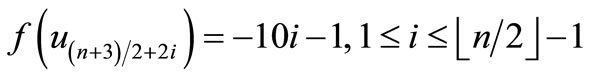
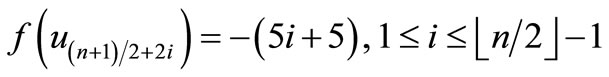

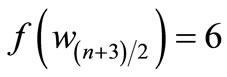
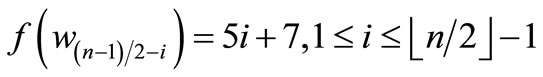
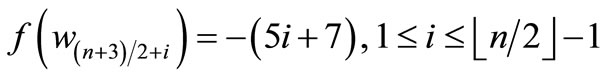
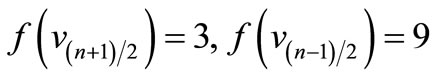
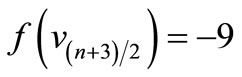
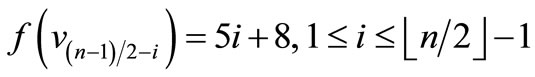
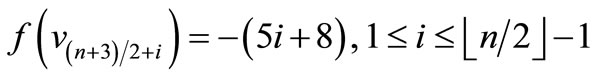
Here
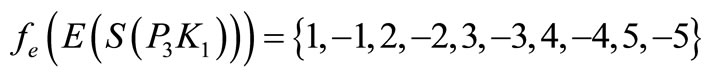
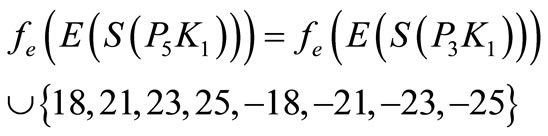
When n > 5,
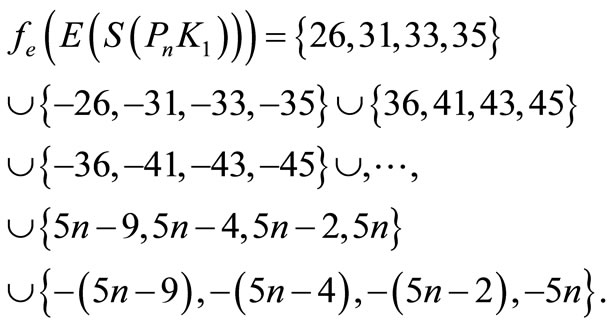
Then f is pair sum labeling.
Illustration 5. A pair sum labeling of 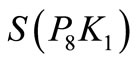 is shown in Figure 5.
is shown in Figure 5.

Figure 5. A pair sum labeling of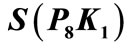 .
.
Theorem 4.4. 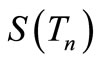 is a pair sum graph where
is a pair sum graph where 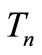 is a triangular snake with n triangle.
is a triangular snake with n triangle.
Proof. Let
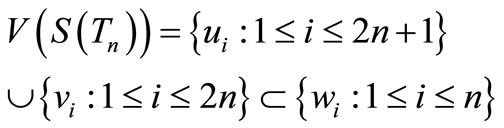
and
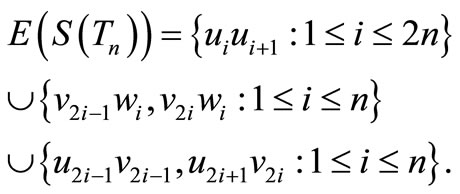
Case 1. n is even.
When n = 2, Define f(u1) = 7, f(u2) = 6, f(u3) = 1, f(u4) = –6, f(u5) = –7, f(v1) = 5, f(v2) = 2, f(v3) = –4, f(v4) = –5, f(w1) = 3, f(w2) = –3. When n > 2, Define
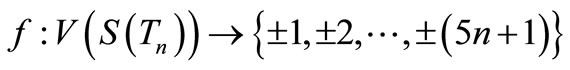
by


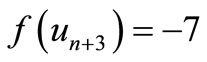
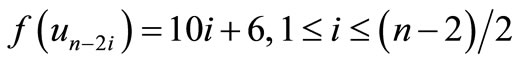
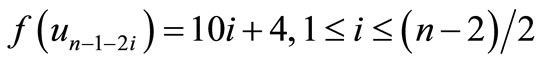
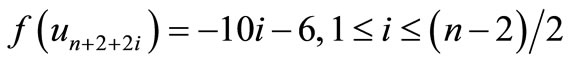
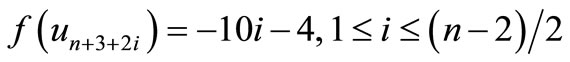
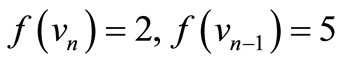
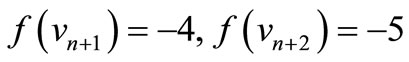

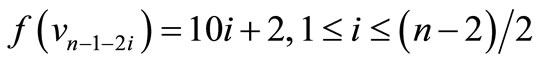
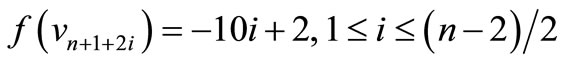
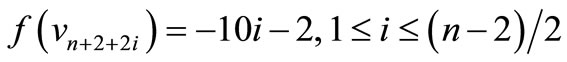
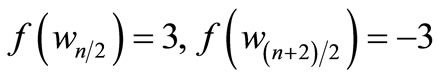
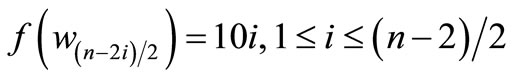
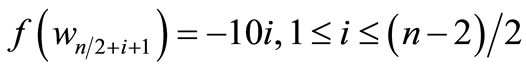
For n = 4,
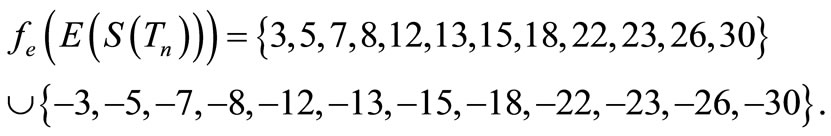
For n > 4
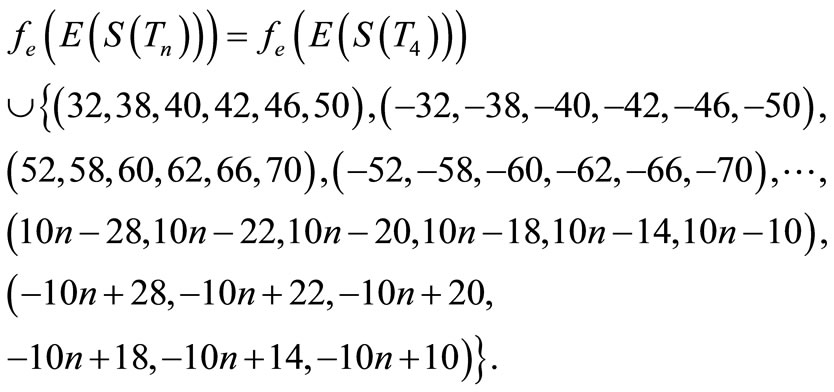
Then f is pair sum labeling.
Case 2. n is odd.
Clearly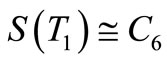 , and hence
, and hence 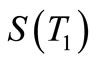 is a pair sum graph by Theorem 2.3.
is a pair sum graph by Theorem 2.3.
For > 1, Define
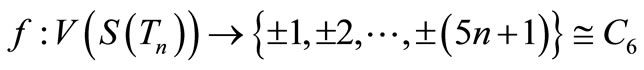
by
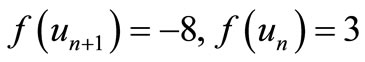
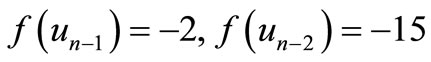


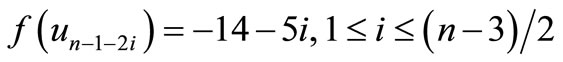

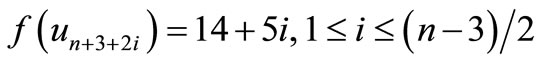
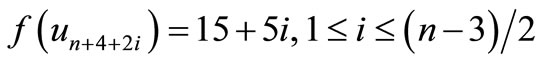
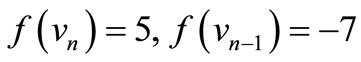

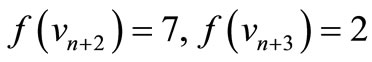

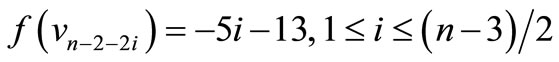
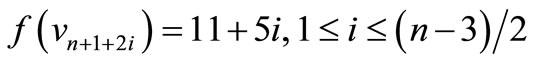
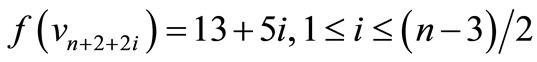
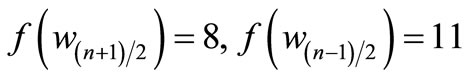
 ,
,
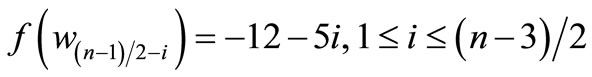
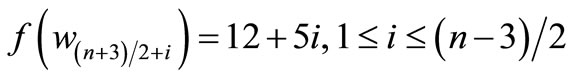
Here n = 3,
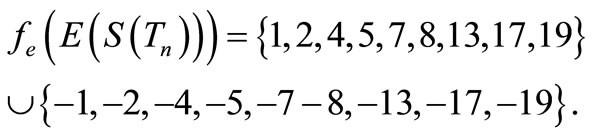
For n > 3,
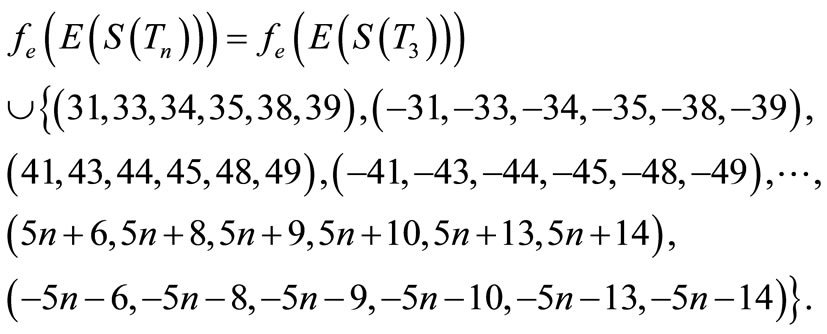
Then f is pair sum labeling.
Illustration 6. A pair sum labeling of  is shown in Figure 6.
is shown in Figure 6.
Theorem 4.5.  is a pair sum graph.
is a pair sum graph.
Proof. Let

and
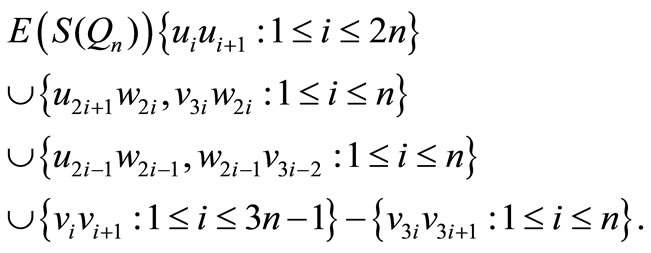
Case 1. n is even.
When n = 2, Define f(u1) = 11, f(u2) = 6, f(u3) = 1, f(u4) = –6, f(u5) = –11, f(w1) = 9, f(w2) = 2, f(w3) = –4, f(w4) = –9, f(v1) = 7, f(v2) = 5, f(v3) = 3, f(v4) = –3, f(v5) = –5, f(v6) = –7. When > 2, Define
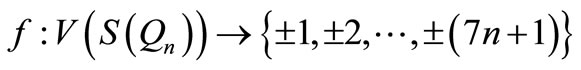
by
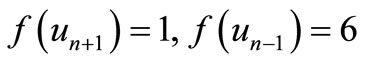
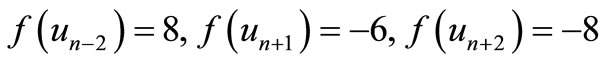
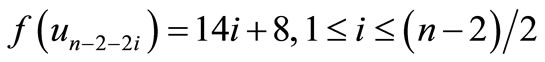
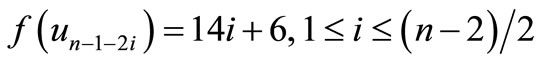
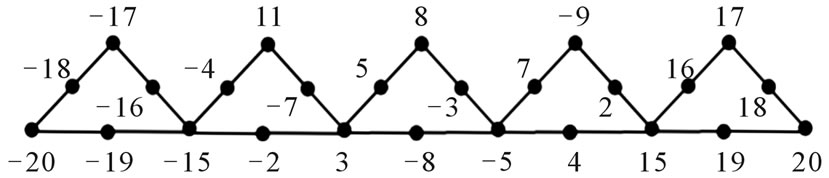
Figure 6. A pair sum labeling of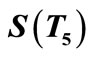 .
.
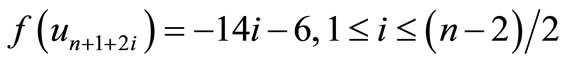
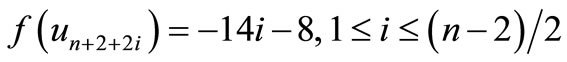

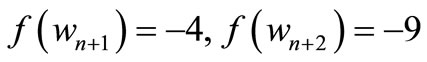
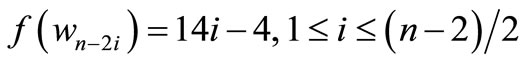

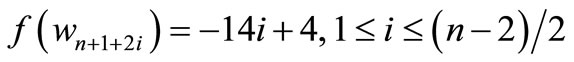


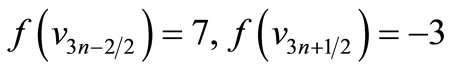
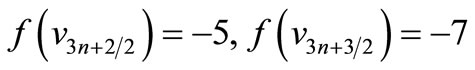
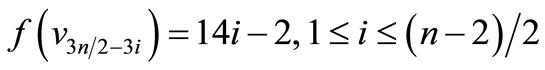
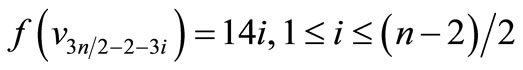


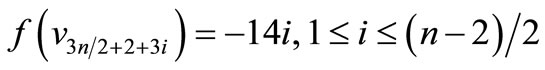
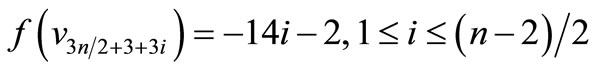
Here

Then f is pair sum labeling.
Case 2. n is odd.
 is a pair sum graph follows from Theorem 2.3.When n > 1. Define
is a pair sum graph follows from Theorem 2.3.When n > 1. Define

by
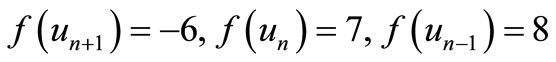


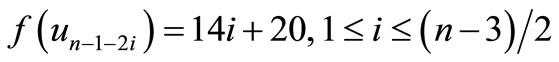
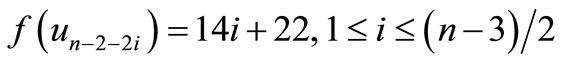
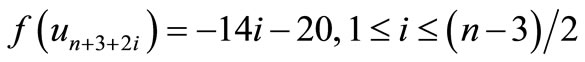
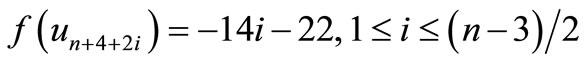

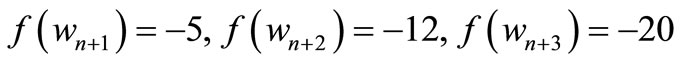
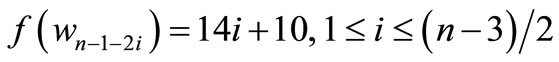
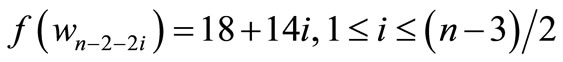
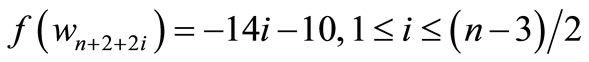

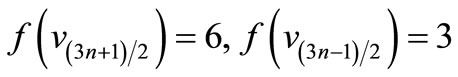
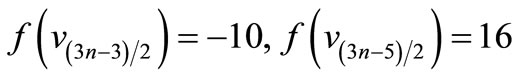

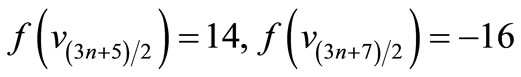
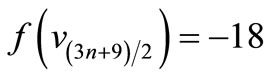
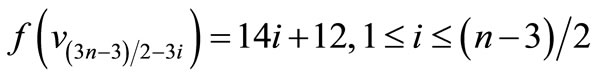
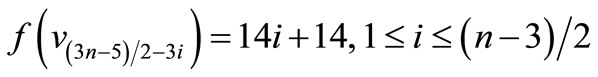
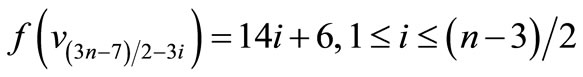
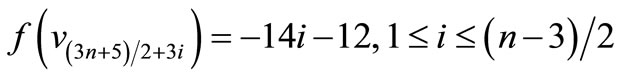
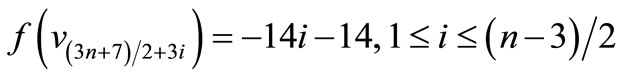
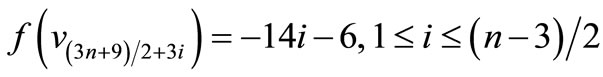
For n = 3,
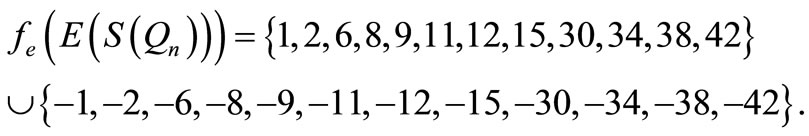
n > 3,
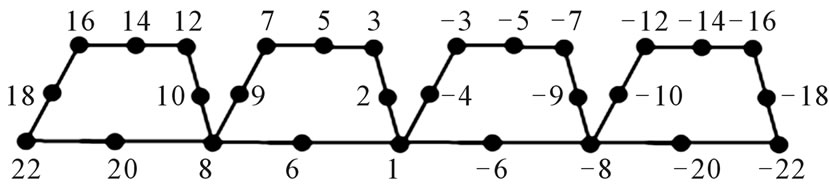
Figure 7. A pair sum labeling of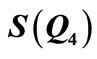 .
.

Then f is pair sum labeling Illustration 7. A pair sum labeling of 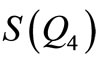 is shown in Figure 7.
is shown in Figure 7.
5. Acknowledgements
We thank the referees for their valuable comments and suggestions.
REFERENCES
- R. Ponraj and J. V. X. Parthipan, “Pair Sum Labeling of Graphs,” The Journal of Indian Academy of Mathematics, Vol. 32, No. 2, 2010, pp. 587-595.
- R. Ponraj, J. V. X. Parthipan and R. Kala, “Some Results on Pair Sum Labeling,” International Journal of Mathematical Combinatorics, Vol. 4, 2010, pp. 53-61.
- R. Ponraj, J. V. X. Parthipan and R. Kala, “A Note on Pair Sum Graphs,” Journal of Scientific Research, Vol. 3, No. 2, 2011, pp. 321-329.
- R. Ponraj and J. V. X. Parthipan, “Further Results on Pair Sum Labeling of Trees,” Applied Mathematics, Vol. 2, No. 10, 2011, pp. 1270-1278. doi:10.4236/am.2011.210177
- F. Harary, “Graph Theory,” Narosa Publishing House, New Delhi, 1998.

