Applied Mathematics
Vol. 3 No. 2 (2012) , Article ID: 17397 , 3 pages DOI:10.4236/am.2012.32029
On a Population Model of Systems 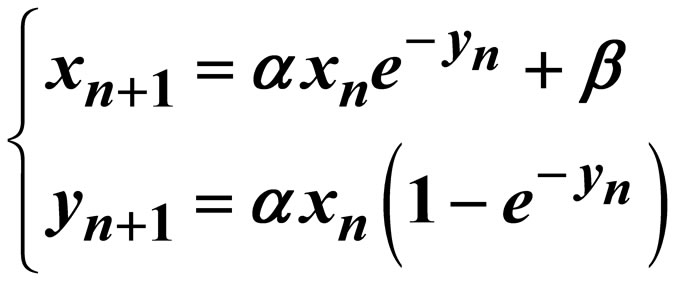 *
*
Institute of Applied Mathematics, Naval Aeronautical and Astronautical University, Yantai, China
Email: dczhang1967@tom.com, ytliyingwang@163.com
Received November 26, 2011; revised February 2, 2012; accepted February 10, 2012
Keywords: Population Model; Global Attractor; Difference Equations
ABSTRACT
In this paper, we investigate the global character of all positive solutions of a population model of systems. Some interesting convergence properties of the solution are given, and lastly, we obtain that the solution is permanent under some conditions.
1. Introduction
In the recent monograph [1, p.129], Kulenovic and Glass give an open problem as follows:
Open problem 6.10.16 (A population model).
Assume that 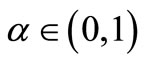 and
and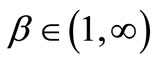 . Investigate the global character of all positive solutions of the systems:
. Investigate the global character of all positive solutions of the systems:
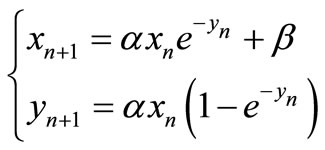 (1)
(1)
where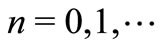 , which may be viewed as a population model.
, which may be viewed as a population model.
To this end, we consider Equation (1) and obtain some interesting results about the positive solutions of Equation (1).
2. Basic Lemma
Lemma 1 Assume that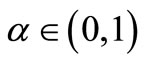 ,
,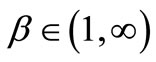 . Then the following statements are true:
. Then the following statements are true:
1) If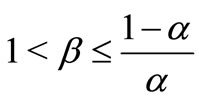 , then Equation (1) has a unique nonegative equilibrium solution as follows:
, then Equation (1) has a unique nonegative equilibrium solution as follows:
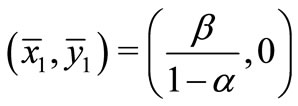
2) If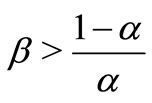 , then Equation (1) has two no-negative equilibrium solutions as follows:
, then Equation (1) has two no-negative equilibrium solutions as follows:
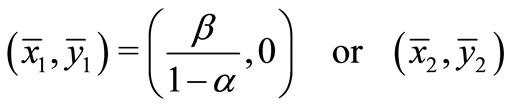
where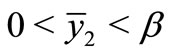 ,
, 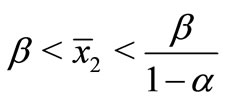 such that
such that
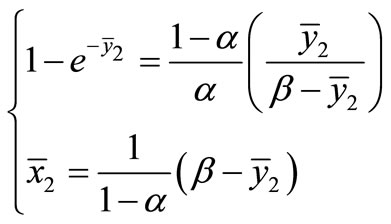 (2)
(2)
Proof: The equilibrium equations about Equation (1) can be written as follows:
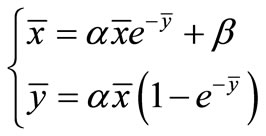 (3)
(3)
It is easy to see that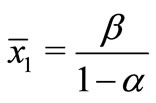 ,
, 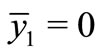 is a group solutions of Equation (3).
is a group solutions of Equation (3).
By (3) we obtain
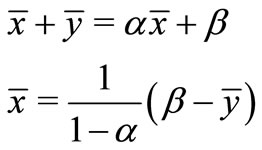 (4)
(4)
Thus
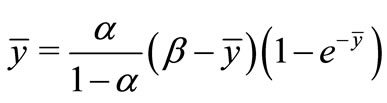 (5)
(5)
Noting that (3) and (4) we get:
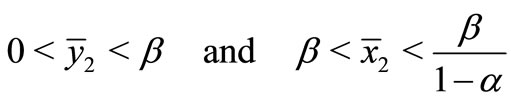
Changing (5) to (6)
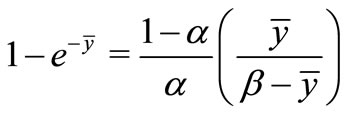 (6)
(6)
Set
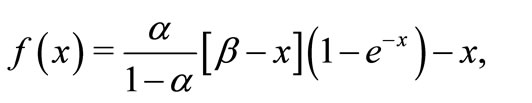
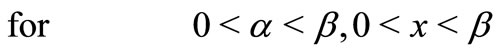
Observing that
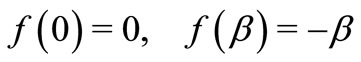
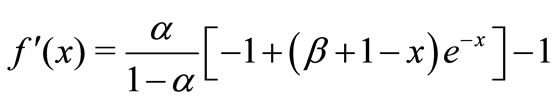
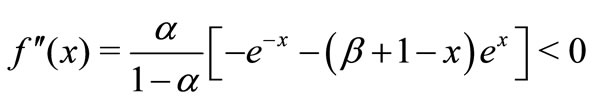
So, by the convex functions properties, if
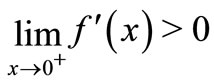 , then we can obtain Equation (6) has a unique positive solution
, then we can obtain Equation (6) has a unique positive solution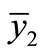 .
.
In fact, by the continuous of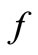 , we can get
, we can get
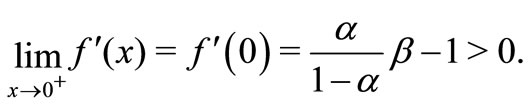
Hence, we complete the proof.
3. Main Results
Theorem 3.1 Assume that 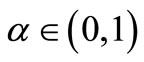 and
and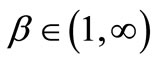 .
.
Then every positive solutions 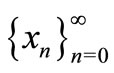 and
and 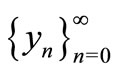 of Equation (1) have the following properties:
of Equation (1) have the following properties:
1)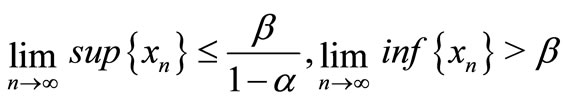 ;
;
2)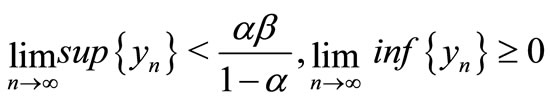 .
.
Proof: By Equation (1) we have
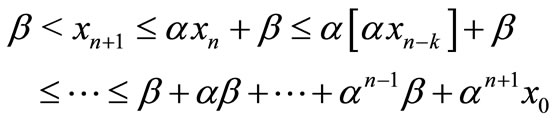
It is to say that 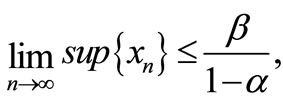
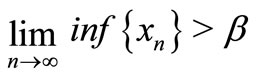 .
.
By Equation (1) we also get
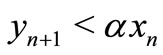
Thus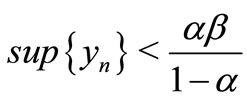 ,
,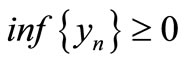 .
.
This completes the proof.
Theorem 3.2 Assume that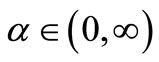 ,
, 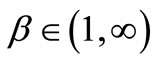
and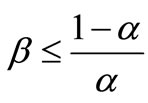 . Then every positive solutions of Equation (1) convergences to the unique no-negative equilibrium solution
. Then every positive solutions of Equation (1) convergences to the unique no-negative equilibrium solution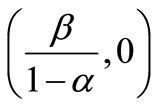 .
.
Proof: By Theorem 3.1, we have that there exists a nature number n0 such that 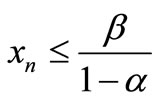 for
for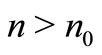 .
.
Hence, by Equation (1) we get
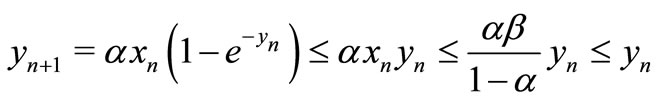
Thus 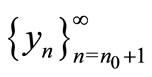 is decreasing.
is decreasing.
Suppose that
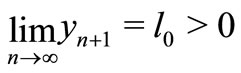 (7)
(7)
Then by Equation (1) we have
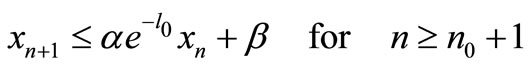
By induction we obtain
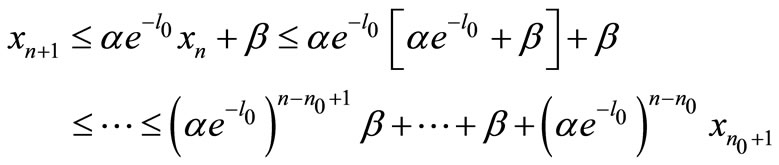
Thus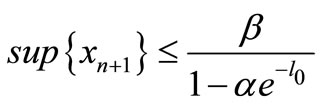 . Hence there exists a
. Hence there exists a 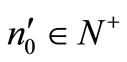 such that
such that 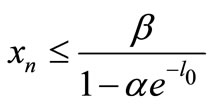 for
for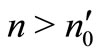 .
.
Noting that Equation (1)
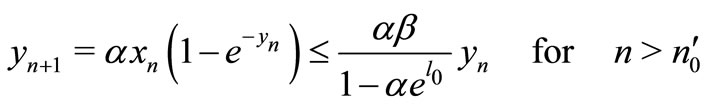
By induction,
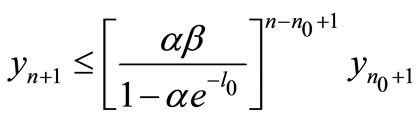
It is to see that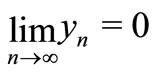 . This is a contradiction with (7), then
. This is a contradiction with (7), then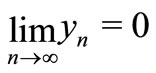 .
.
Noting that Equation (1) we have
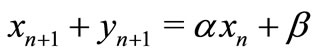
i.e.
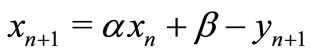
Let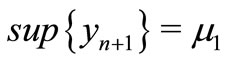 ,
,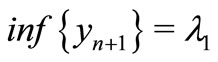 . Then
. Then
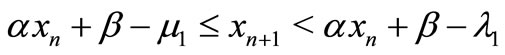
By induction we obtain
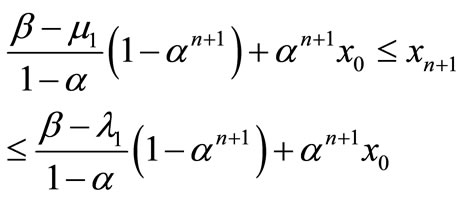
as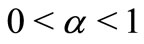 , then
, then
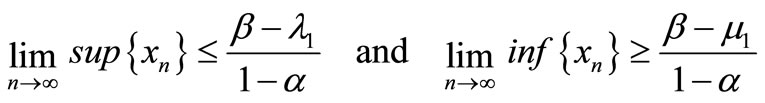 (8)
(8)
Because of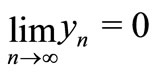 , we obtain that
, we obtain that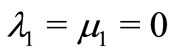 .
.
Hence
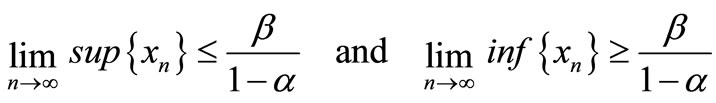 (9)
(9)
By (9) we get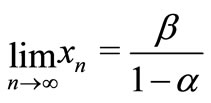 .
.
We complete the proof.
Theorem 3.3 Assume that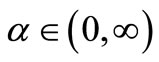 ,
, 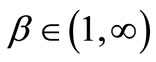 and
and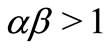 . Then Equation (1) is permanent.
. Then Equation (1) is permanent.
Proof: By Equation (1) we obtain
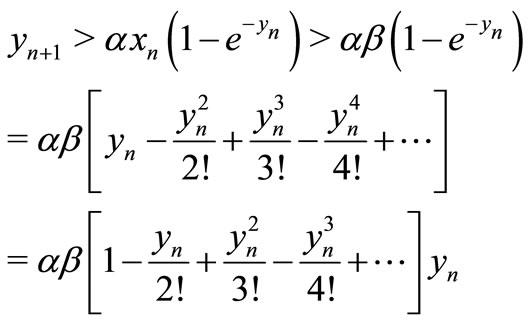
There exists two positive constants 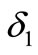 and
and 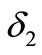 such that
such that
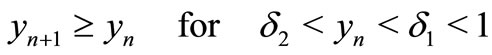
Hence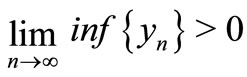 .
.
Using Theorem 3.1, we complete the proof.
REFERENCES
- M. R. S. Kulenovic and G. Ladas, “Dynamics of Second Order Rational Difference Equations,” Chapman & Hall/ CRC, Boca Raton, 2002.
NOTES
*Research supported by Distinguished Expert Foundation and Youth Science Foundation of Naval Aeronautical and Astronautical University.

