Applied Mathematics
Vol. 3 No. 1 (2012) , Article ID: 16766 , 5 pages DOI:10.4236/am.2012.31012
Uniqueness of Common Fixed Points for a Family of Mappings with 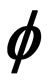 -Contractive Condition in 2-Metric Spaces*
-Contractive Condition in 2-Metric Spaces*
Department of Mathematics, College of Science, Yanbian University, Yanji, China
Email: pyj6216@hotmail.com
Received November 4, 2011; revised December 14, 2011; accepted December 22, 2011
Keywords: 2-metric space; 5-dimensional functions ;
; 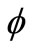 -contractive condition; Cauchy sequence; common fixed point
-contractive condition; Cauchy sequence; common fixed point
ABSTRACT
In this paper, we will introduce a class of 5-dimensional functions 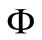 and prove that a family of self-mappings
and prove that a family of self-mappings  in 2-metric space have an unique common fixed point if 1)
in 2-metric space have an unique common fixed point if 1)  satisfies
satisfies 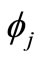 -contractive condition, where
-contractive condition, where , for each
, for each ; 2)
; 2) 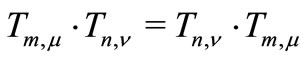 for all
for all 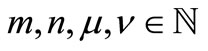 with
with . Our main result generalizes and unifies many known unique common fixed point theorems in 2-metric spaces.
. Our main result generalizes and unifies many known unique common fixed point theorems in 2-metric spaces.
1. Introduction and Preliminaries
There have appeared many unique common fixed point theorems for self-maps 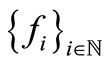 with some contractive condition on 2-metric spaces. But most of them held under subsidiary conditions [1-4], for examples: commutativity of
with some contractive condition on 2-metric spaces. But most of them held under subsidiary conditions [1-4], for examples: commutativity of  or uniform boudedness of
or uniform boudedness of 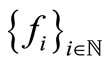 at some point, and so on. In [5], the author obtained similar results under removing the above subsidiary conditions. The result generalized and improved many same type unique common fixed point theorems. Recently, the author discussed unique common fixed point theorems for a family of contractive or quasi-contractive type mappings on 2-metric spaces, see [6-8], these results improve the above known common fixed point theorems.
at some point, and so on. In [5], the author obtained similar results under removing the above subsidiary conditions. The result generalized and improved many same type unique common fixed point theorems. Recently, the author discussed unique common fixed point theorems for a family of contractive or quasi-contractive type mappings on 2-metric spaces, see [6-8], these results improve the above known common fixed point theorems.
In this paper, in order to generalize and unify further these results, we will prove that a family of self-maps 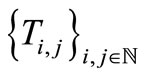 satisfying
satisfying 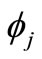 -contractive condition on 2-metric spaces have an unique common fixed point if
-contractive condition on 2-metric spaces have an unique common fixed point if 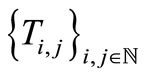 satisfy the condition 2.
satisfy the condition 2.
The following definitions are well known results.
Definition 1.1. [4] 2-metric space 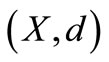 consists of a nonempty set
consists of a nonempty set  and a function
and a function  such that 1) for distant elements
such that 1) for distant elements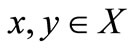 , there exists an
, there exists an 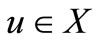 such that
such that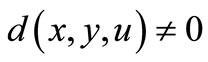 ;
;
2) 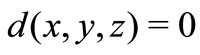 if and only if at least two elements in
if and only if at least two elements in 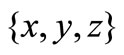 are equal;
are equal;
3)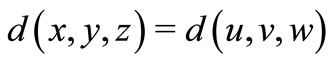 , where
, where 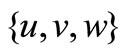 is any permutation of
is any permutation of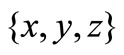 ;
;
4)  for all
for all .
.
Definition 1.2. [4] A sequence 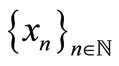 in 2-metric space
in 2-metric space 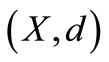 is said to be cauchy sequence, if for each
is said to be cauchy sequence, if for each  there exists a positive integer
there exists a positive integer 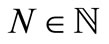 such that
such that  for all
for all 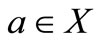 and
and .
.
Definition 1.3. [4,5] A sequence 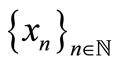 is said to be convergent to
is said to be convergent to , if for each
, if for each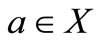 ,
, 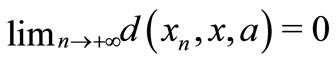 . And write
. And write  and call
and call 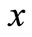 the limit of
the limit of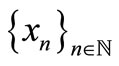 .
.
Definition 1.4. [4,5] 2-metric space 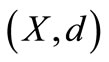 is said to be complete, if every cauchy sequence in
is said to be complete, if every cauchy sequence in  is convergent.
is convergent.
Let 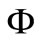 denotes a family of mappings such that each
denotes a family of mappings such that each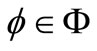 ,
, 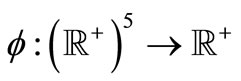 is continuous and increasing in each coordinate variable, and
is continuous and increasing in each coordinate variable, and 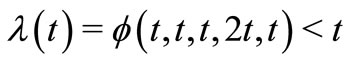 for all
for all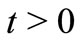 .
.
There are many functions 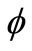 which belongs to
which belongs to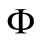 :
:
Example 1.5. Let 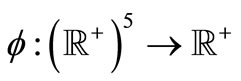 be defined by
be defined by

Then obviously, 
Example 1.6. Let 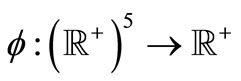 be defined by
be defined by
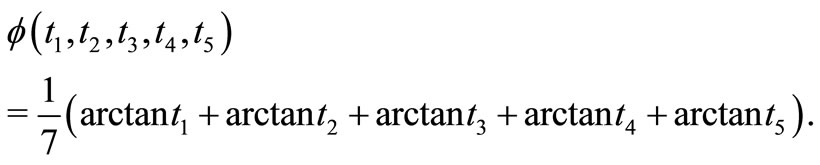
Then obviously, 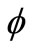 is continuous and increasing in each coordinate variable, and
is continuous and increasing in each coordinate variable, and

Hence 
The following two lemmas are known.
Lemma 1.7. [1-4] Let  be a 2-metric space and
be a 2-metric space and  a sequence. If there exists
a sequence. If there exists 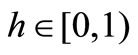 such that
such that 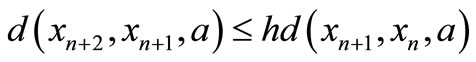 for all
for all 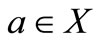 and
and
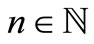 , then
, then  for all
for all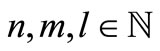 , and
, and
 is a cauchy sequence Lemma 1.8. [1-4] If
is a cauchy sequence Lemma 1.8. [1-4] If  is a 2-metric space and sequence
is a 2-metric space and sequence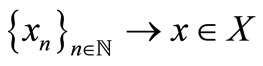 , then
, then 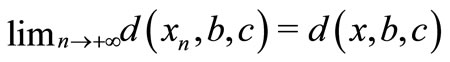 for each
for each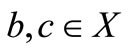 .
.
2. Main Result
The following theorem is the main result in this present paper.
Theorem 2.1. Let 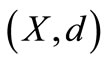 be a complete 2-metric space,
be a complete 2-metric space, 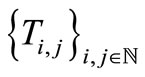 a family of maps from
a family of maps from 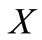 into itself,
into itself, 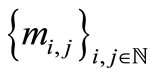 a family of positive integers, and
a family of positive integers, and 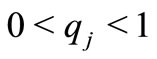 and
and 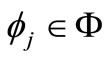 for each
for each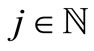 . If the following
. If the following  - contractive conditions hold
- contractive conditions hold
 (1)
(1)
and 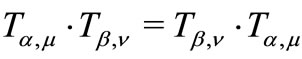 for all
for all  with
with . Then
. Then 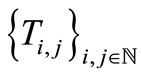 have an unique common fixed point in X.
have an unique common fixed point in X.
Proof Fix 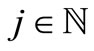 and let
and let  for each
for each , then (1) becomes the following
, then (1) becomes the following
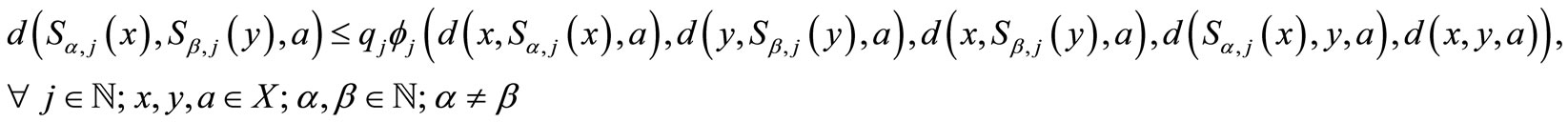 (2)
(2)
Take an 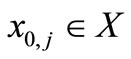 and define a sequence as follows
and define a sequence as follows
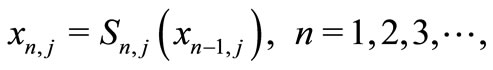
Then
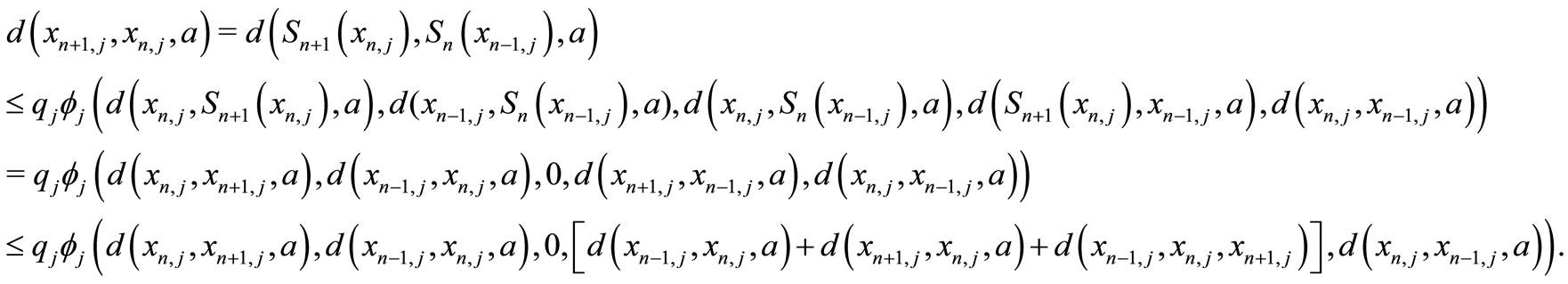 (3)
(3)
If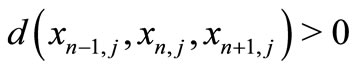 , then
, then
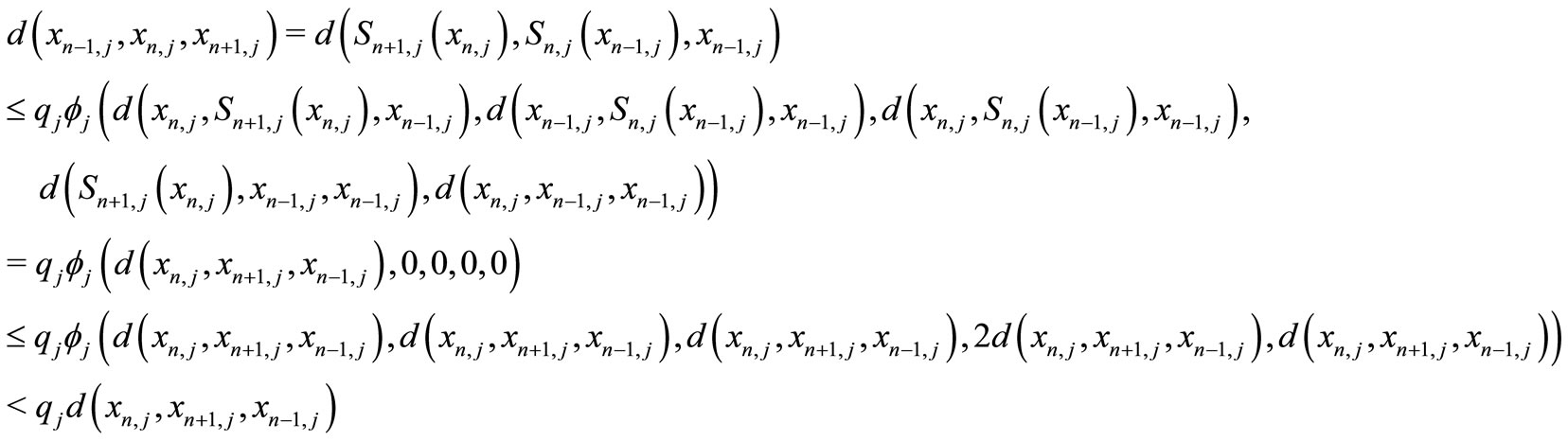 (4)
(4)
which is a contradiction since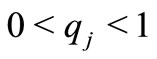 , hence
, hence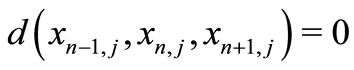 . And therefore, (3) becomes
. And therefore, (3) becomes
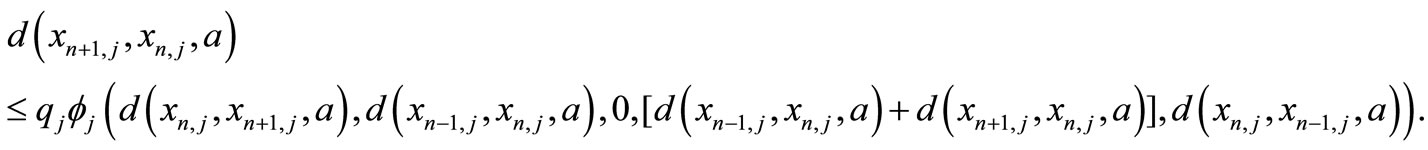 (5)
(5)
If there exists an  such that
such that , then (5) becomes
, then (5) becomes
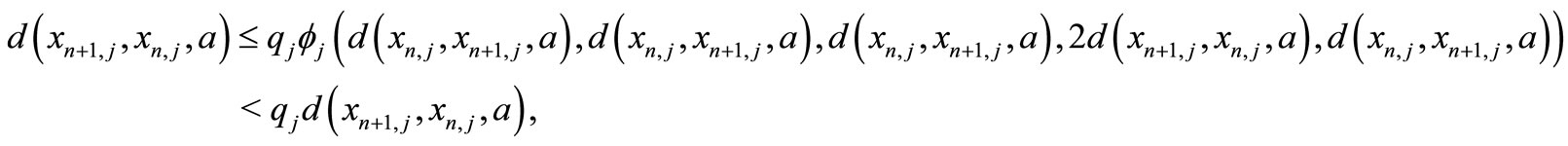
which is a contradiction since  and
and 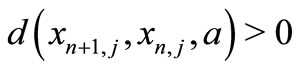 , hence he have that
, hence he have that 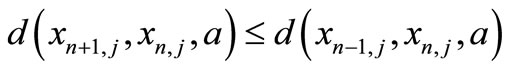 for all
for all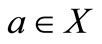 . In this case, (5) becomes
. In this case, (5) becomes
 (6)
(6)
(6) implies that  is a cauchy sequence by Lemma 1, hence by the completeness of
is a cauchy sequence by Lemma 1, hence by the completeness of ,
,  converges to some element
converges to some element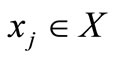 . (7)
. (7)
Now, we prove that  is the unique common fixed point of
is the unique common fixed point of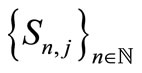 . In fact, for any fixed
. In fact, for any fixed  and any
and any  with
with  and any
and any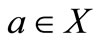 ,
,
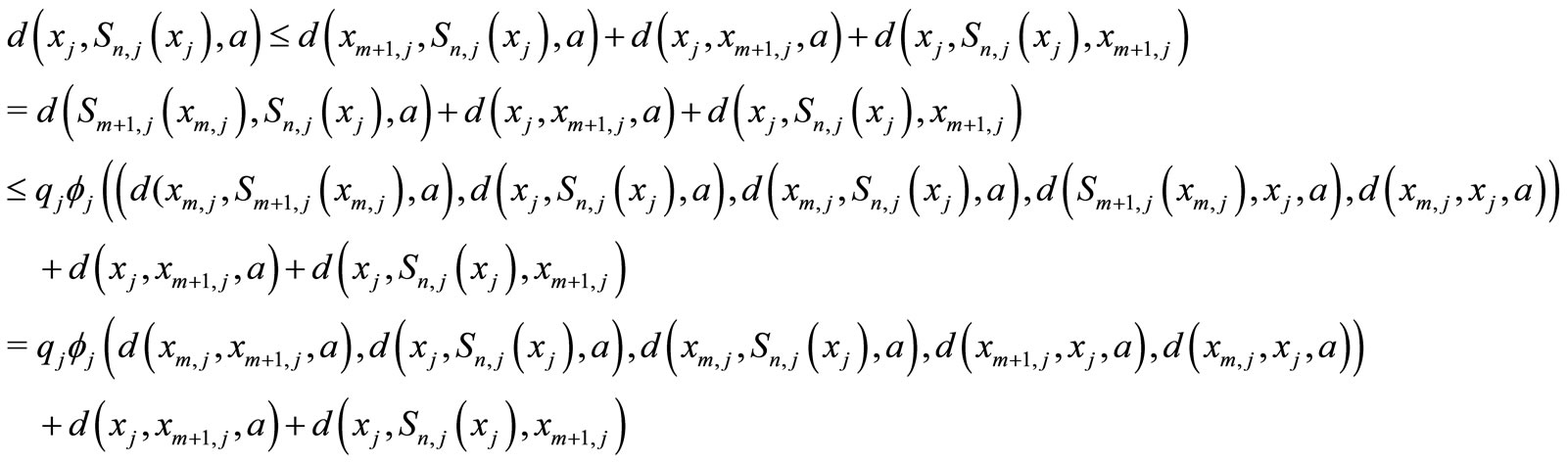
Let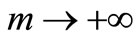 , then by Lemma 2, the continuity of
, then by Lemma 2, the continuity of 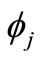 and (7), the above becomes
and (7), the above becomes
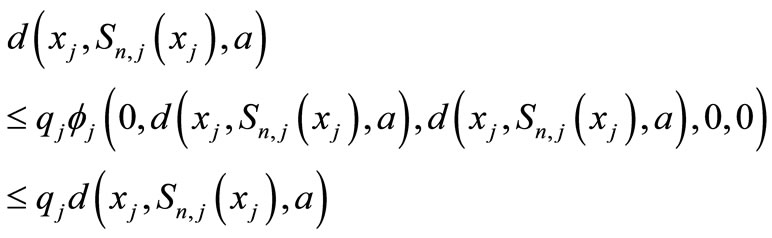 .
.
But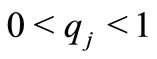 , hence
, hence 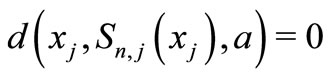 for all
for all
 , and therefore,
, and therefore, 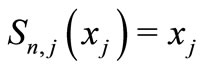 for all
for all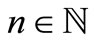 .
.
This completes that 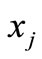 is a common fixed point of
is a common fixed point of
 .
.
Let 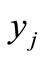 be a common fixed point of
be a common fixed point of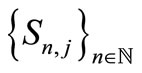 , If there exists an
, If there exists an 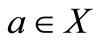 such that
such that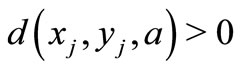 , then
, then
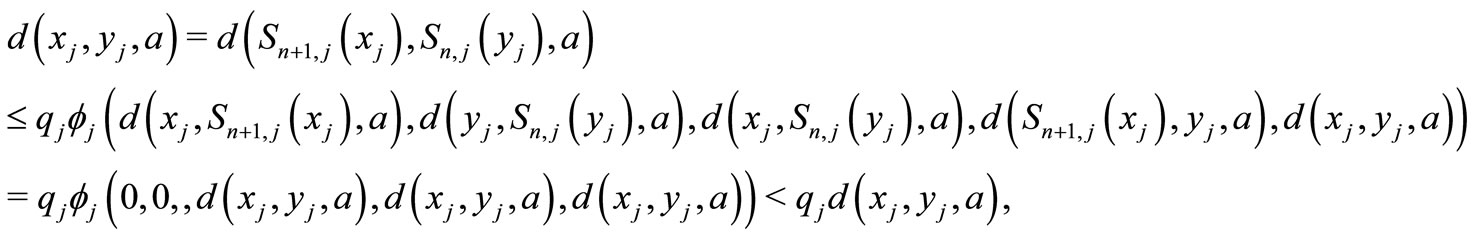
which is a contradiction since , hence
, hence  for all
for all , and therefore
, and therefore . This completes that
. This completes that  has an unique common fixed point
has an unique common fixed point  for all
for all .
.
Next, we will prove that  is the unique common fixed point of
is the unique common fixed point of  for each fixed
for each fixed . Indeed, for fixed
. Indeed, for fixed , Since
, Since 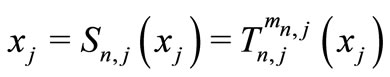 for each
for each , hence
, hence
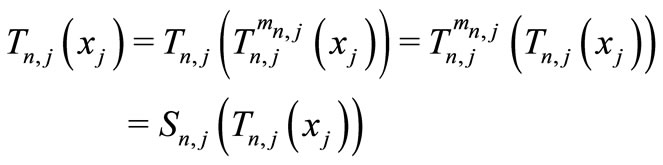
for each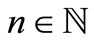 , which means that
, which means that  is a fixed point of
is a fixed point of 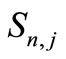 for each
for each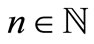 . Now, fix
. Now, fix 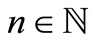 and let
and let 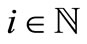 with
with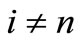 , if there exists an
, if there exists an 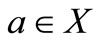 such that
such that  , then
, then
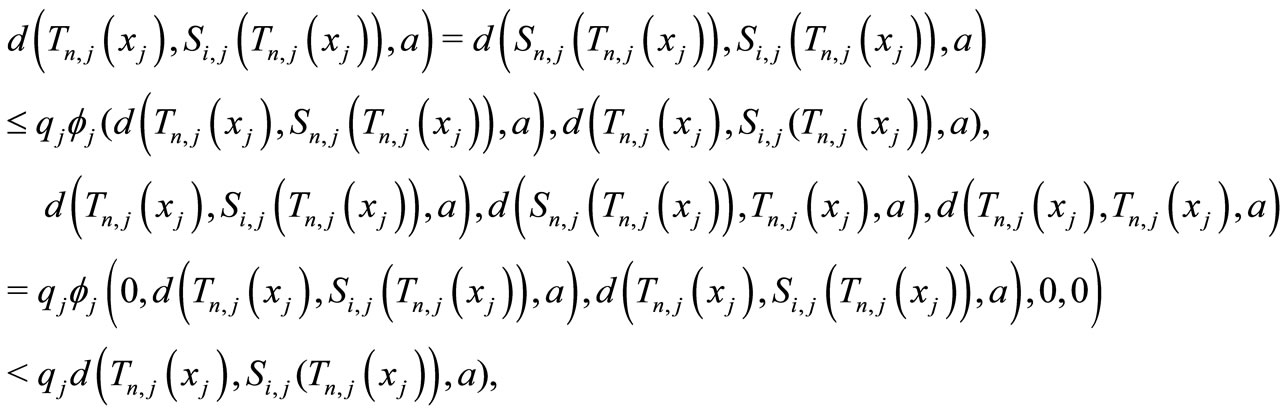
which is a contradiction since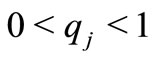 , hence
, hence
 for all
for all , and therefore
, and therefore . This means that
. This means that
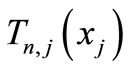 is a common fixed point of
is a common fixed point of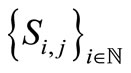 . But
. But 
is the unique common fixed point of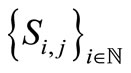 , hence
, hence
 for all
for all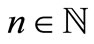 , which means that
, which means that 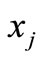 is a common fixed point of
is a common fixed point of 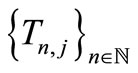 for all
for all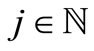 .
.
If 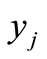 is a common fixed point of
is a common fixed point of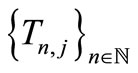 , then
, then 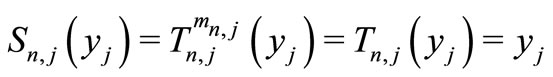 for all
for all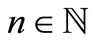 , which means that
, which means that 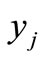 is a common fixed point of
is a common fixed point of
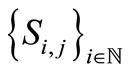 . But
. But 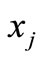 is the unique common fixed point of
is the unique common fixed point of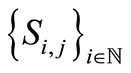 , hence
, hence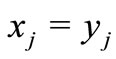 . This completes that
. This completes that 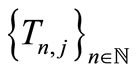
has the unique common fixed point 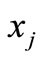 for each
for each .
.
Finally, we will prove that 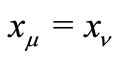 for all
for all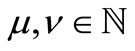 . In fact, for any fixed
. In fact, for any fixed 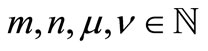 with
with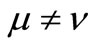 , since
, since 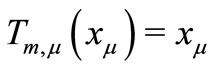 and
and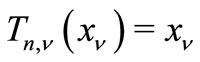 , hence
, hence
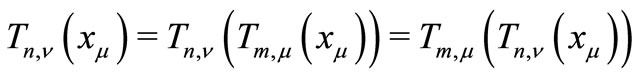 by condition 2). Which means that
by condition 2). Which means that 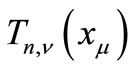 is a common fixed point of
is a common fixed point of 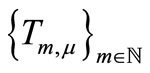 for all
for all . But the unique common fixed point of
. But the unique common fixed point of 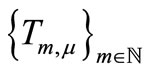 is
is , hence
, hence
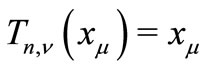 for all
for all , this means that
, this means that  is a common fixed point of
is a common fixed point of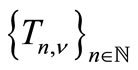 , and therefore
, and therefore
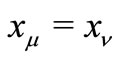 since
since 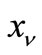 is the unique common fixed point of
is the unique common fixed point of . Let
. Let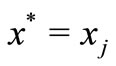 , then
, then  is the unique common fixed point of
is the unique common fixed point of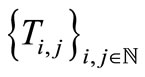 .
.
The following is a particular form of Theorem 2.1:
Theorem 2.2. Let 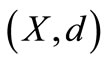 be a complete 2-metric space,
be a complete 2-metric space, 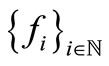 a family of maps from
a family of maps from 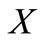 into itself and
into itself and  and
and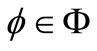 . If the following
. If the following  -contractive condition holds
-contractive condition holds
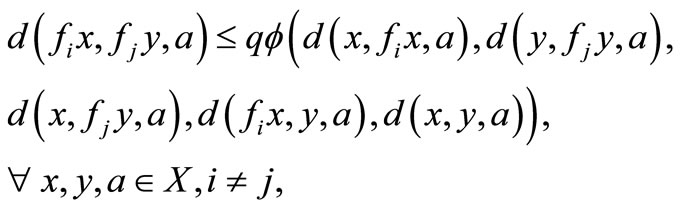
then 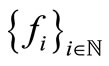 has an unique common fixed point in
has an unique common fixed point in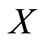 .
.
Next theorem is the main result in [5].
Theorem 2.3. Let 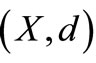 be a complete 2-metric space,
be a complete 2-metric space,  a family of maps from
a family of maps from 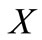 into itself. If there exist a family non-negative integers
into itself. If there exist a family non-negative integers 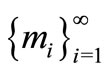 and nonnegative real numbers
and nonnegative real numbers 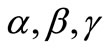 with
with 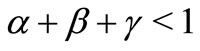 such that for all
such that for all 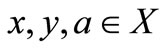 and all natural numbers
and all natural numbers 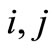 with
with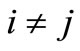 , the following holds
, the following holds
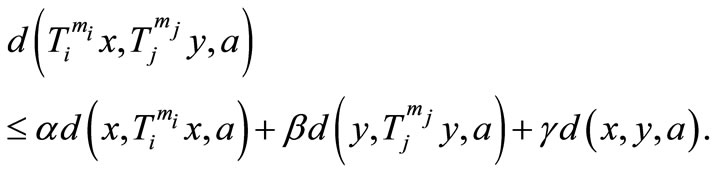
Then  have an unique common fixed point in
have an unique common fixed point in .
.
Remark. Obviously, Theorem 2.3 is a very particular form of Theorem 2.1. In fact, Let
 , and take
, and take
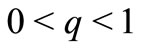 satisfying
satisfying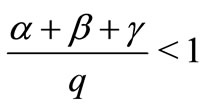 , then
, then  and
and  satisfy all conditions of Theorem 2.1. Hence we sure that our main result generalized and improve many corresponding common fixed point theorems in 2-metric spaces.
satisfy all conditions of Theorem 2.1. Hence we sure that our main result generalized and improve many corresponding common fixed point theorems in 2-metric spaces.
REFERENCES
- Y. J. Piao, G. Z. Jin and B. J. Zhang, “A family of selfmaps having an unique common fixed point in 2-metric spaces,” Yanbian University (Natural Science), Vol. 28, No. 1, 2002, pp. 1-5.
- H. S. Yang and D. S. Xiong, “A common fixed point theorem on p-metric spaces,” Journal of Yunnan Normal University (Science Edition), Vol. 21, No. 1, 2001, pp. 9- 12.
- S. L. Singh, “Some contractive type principles on 2-Metric spaces and applications,” Mathematics Seminar Notes (Kobe University), Vol. 7, No. 1, 1979, pp. 1-11.
- I. S. Kim, “Common fixed point theorems in 2-metric spaces,” Master’s Thesis, Korea Soongsil University, Seoul, 1994.
- Y. J. Piao and Y. F. Jin, “Unique common fixed point theorem for a family of contractive type non-commuting selfmaps in 2-metric spaces,” Journal of Yanbian University (Science Edition), Vol. 32, No. 1, 2006, pp. 1-3.
- Y. J. Piao, “A family of quasi-contractive type noncommutative self-maps having an unique common fixed point in 2-metric spaces,” Journal of Heilongjiang University (Science Edition), Vol. 23, No. 5, 2006, pp. 655- 657.
- Y. J. Piao, “Unique common fixed point for a family of self-maps with same type contractive condition in 2- Metric spaces,” Analysis in Theory and Applications, Vol. 24, No. 4, 2008, pp. 316-320. doi:10.1007/s10496-008-0316-9
- Y. J. Piao, “Unique common fixed point for a family of self-maps with same quasi-contractive type condition in 2-metric space,” Journal of Nanjing University (Mathematical Biquarterly), Vol. 27, No.1, 2010, pp. 82-87.
NOTES
*This paper is Supported by the Foundation of Education Ministry, Jilin Province, China (No: 2011[434]).

