Wireless Engineering and Technology
Vol.2 No.3(2011), Article ID:5832,12 pages DOI:10.4236/wet.2011.23028
Processor for Measuring Radio Network Design Quality
![]()
1Department of Technologies of Computers and Communications, Polytechnic School, University of Extremadura, Cáceres, Spain; 2School of Technology and Management, Polytechnic Institute of Leiria, Leiria, Portugal.
Email: jangomez@unex.es
Received October 30th, 2010, revised December 27th, 2010; accepted February 9th, 2011.
Keywords: Radio Networks, Reconfigurable Computing, Optimization, Parallelism
ABSTRACT
In this paper we present the design and prototyping of an arithmetic processor based on reconfigurable technology, whose purpose is to determine in a parallel manner the quality of the solution in a radio network design optimization problem. This problem consists in the search for an optimal set of locations in which to place radio antennas in order to obtain the maximum possible coverage, for a given terrain and antenna characteristics. The original computational contribution of this work is to use programmable logic devices to avoid the high cost of computing the evolutionary algorithms required to tackle this optimization problem. This is achieved by means of reconfigurable processors working in parallel. On the basis of the results obtained from the prototype, it may be considered a parallel architecture capable of achieving a great acceleration in the calculations.
1. Introduction
The Radio Network Design Problem (RND) originated in the context of wireless communication technologies. An efficient design of a radio transmitting network is a relevant issue due to the continuous increase in the user population of the radio-communications-associated services which demand more efficient coverage in wide geographic areas. The RND problem is an optimization problem belonging to NP-Hard class: there are a great number of possible solutions, prohibiting the determination of the optimal one through their sequential evaluation. That is why several optimization algorithms are normally used instead.
In short, the RND problem consists of minimizing the number of transmitting base stations (referred to from here on as antennas) and establishing their optimal locations, with the goal of obtaining the maximum coverage area and providing services to a larger number of terminals.
An antenna transmits a radio signal according to its type of coverage. In this work we consider propagation models of simplified waves such as the omni-directional and squared, with variable radius. In addition we have defined a digital model of the ground, in which the area is divided into sectors and locations that act as nuclear units of information. Thus, the area consists of a rectangular network, where each coordinate (x, y) represents a possible antenna location. The assumption is that there is a fixed amount of valid locations to place antennas.
Figure 1 presents a simple example of the problem, wherein we search for a set of antennas which can reach the maximum coverage area in a terrain of 257 × 257 points, with 349 predefined valid locations for antennas with omni-directional coverage of 35-point radius. Depending on the choice of the antenna locations, the resulting coverage can be completely different.
If some antennas are close enough to one another, their coverage areas overlap, so the locations inside these areas can have different degrees of coverage. For this reason, the information stored in each position of the network must reflect the following data:
• Degree of coverage.
• Whether it is a predefined position available for the placement of an antenna.
• Whether or not an antenna is placed there.
• Antenna propagation type (square or omni-directional).
A fitness function (F) can be used to measure the quality
 (a) (b)
(a) (b)
Figure 1. (a) 61% coverage; (b) 74% coverage.
of a set of antennas placed in any given manner in the network. This fitness function can be obtained from the coverage rate and the number of antennas [1,2], as shown in Equation (1):
 (1)
(1)
In a real study of this problem we have to determine in the first place the set of available localizations for the antennas, excluding those where they cannot be placed (public areas, certain roofs, rivers, etc.). Afterwards the goal is to achieve the maximum level of coverage for the smallest number of antennas. This is a NP-Hard optimization problem for which some evolutionary algorithms (EA) have been successfully tested [3,4].
One important consideration in evolutionary computing is the speed with which the optimal solution is achieved, because of the high computational cost even when it is running on a high-performance machine. Taking into account that many optimization problems can be tackled by parallel methodologies [5,6], we have developed a specific-purpose processor that runs a fitness function in a stand-alone way, so as to implement a set of fitness processors working in parallel on the same chip, using reconfigurable hardware. By this means the computer, besides monitoring and controlling the EA, can be used for any other task with the whole potential of its resources, because it is released from the EA computation effort. The combination of parallelism and hardware implementation allows an increase in the speed of the system as compared with an algorithm implemented by software and performed on a general purpose computer, as explained in Figure 2.
The radio network design quality is here intended for the best deployment of antennas on a determined terrain, minimizing the number of base station transmitters and maximizing the covered area by means of evolutionary algorithms, where the quality of the solution is given by the fitness function. Nevertheless, many other works have considered using network simulators to measure the radio network design quality. Two basic examples are quickly commented representing this kind of studies. Ivanov et al. [7] present the validation of one wireless network model built with ns-2 done by comparing the network characteristics of a simulated, an emulated, and a real wireless network; and Laiho et al. [8] use different simulators (static prediction and dynamic analysis) in order to improve the capacity and Quality of Service of the radio network.
2. Fitness Processor Prototype
The reconfiguration of circuitry at runtime to suit the application at hand has created a promising paradigm of computing that blurs traditional frontiers between software and hardware. This powerful computing paradigm, named reconfigurable computing (RC) [9,10], is based on the use of programmable logic devices, mainly field programmable gate arrays (FPGAs) [11] incorporated in board-level systems. FPGAs have the benefits of hardware speed and software flexibility, hence being a good option for many real scientific and engineering applications [12].
The interest of a hardware solution based on FPGAs is to determine whether it is profitable to run an evolutionary algorithm accelerating some of its calculations. Since the biggest resource consumption comes from the arithmetical computation of the fitness, we have designed and implemented an arithmetical processor to relieve the main processor from this task, introducing the largest possible degree of parallelism. This way, the processor here described is not designed for simulating purposes, but for accelerating the evaluation of the quality of a determined radio deployment solution, inside a wide real radio network design framework. The prototype designed carries out a coverage evaluation for simple configurations of the problem. The aim was to evaluate its performance and to acquire knowledge and experience in the architecture. The architecture design is conditioned by the FPGA characteristics and the prototyping board. For this reason we opted for several boards (Digilent XUPV2P, Enterpoint Broaddown2 and PLDA PCIXSYSV5) with FPGAs of different technologies, as shown in Figure 3. The characteristics of the FPGAs on these boards in relation to the general purpose processors are listed in Table 1.
The problem used for this fitness processor has the following characteristics:
• 287 × 287-point network.
• 349 allowed positions (predefined).
• 49 antennas.
This processor allows configuration of the antenna type (square-shaped or omni-directional coverage) and its maximum propagation radius. To select any configuration, it is enough to modify the value of certain registers

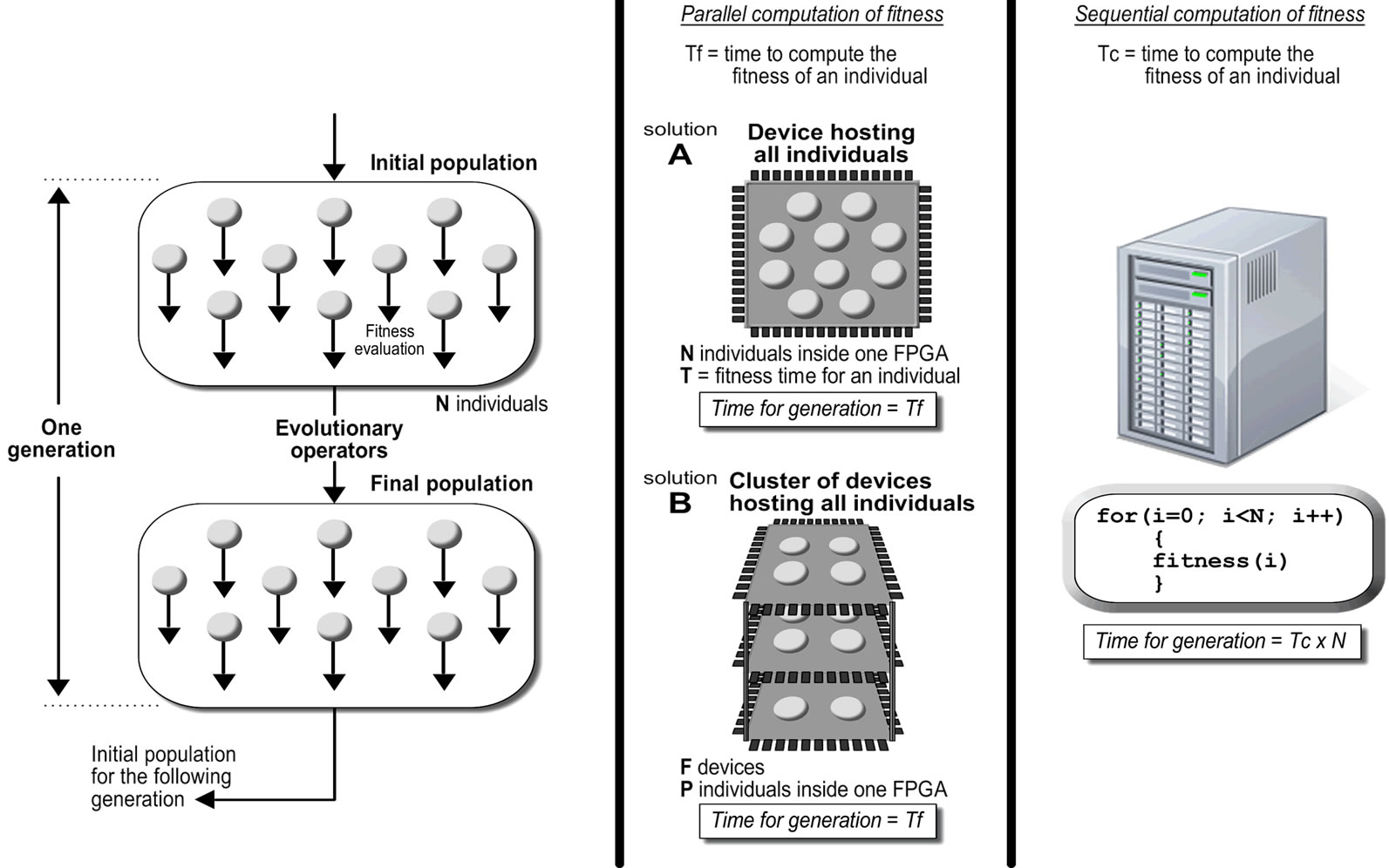
Figure 2. When computing an EA, the fitness of all individuals in a population must be evaluated. We can take advantage of FPGAs where (in contrast with CPUs) parallel computation of the fitness can be realized.

Figure 3. Prototyping boards used in this work.

Table 1. Hardware resources used in this work, arranged by reconfigurable versus general-purpose hardware with similar technology in order to make an effective comparison of results.
through board switches. In order to measure the board execution time and determine its efficiency, the processor carries out 1000 fitness evaluations in a sequential manner. Then the average time of an evaluation is obtained.
Figure 4 presents the top-level architecture of the prototyped processor. The processor uses an on-chip memory where the characteristics of the terrain are stored, so each network point is linked to a 2-byte memory word in a 82,369 address map to represent the 287 × 287 network. Each memory word stores the information as shown in Figure 5.
The controller is the most important unit in the processor. It was programmed in Handel-C [13] and compiled to VHDL. This controller processes the main operations of the coverage calculation, with the exception of the floating-point arithmetic operations, which are carried out by other units. In addition, the controller manages the initialization, evolution and ending of the process, the input/output communication and the accomplishment of the memory writes and reads.
The mathematical operations for the omni-directional coverage and for the fitness function require floatingpoint arithmetic, such as addition, multiplication, power and square root. For this purpose we have designed two co-processors that carry out the necessary operations. The results from these floating-point co-processors are sent to the controller, which uses them for the final coverage processing.
The fitness processor was implemented using the synthesis tool Xilinx ISE 9.1i with the default options for synthesis and implementation steps. The results are shown in Table 2. The occupation of the area (number of occupied FPGA slices) gives us the basis on which to calculate the maximum number of fitness processors able to work in parallel in the same FPGA device. Also, the maximum reported operation frequency is used to select the proper frequency for the on-board oscillator. After generating and loading the configuration bit stream onto the FPGA, the processor gave the results with an elapsed time measured using the existing displays on the board. The results obtained (fitness and coverage) were stored
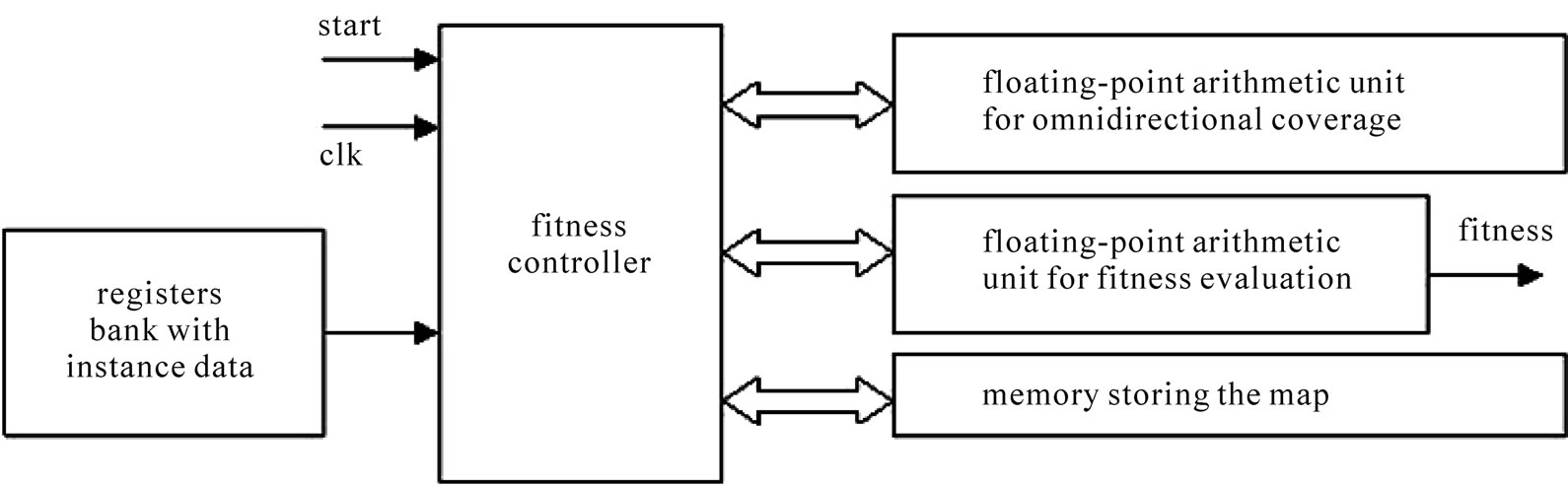
Figure 4. Processor RND fitness processor diagram.

Figure 5. A two-bytes memory word stores the needed data of a point on the map: coverage degree, availability and location.
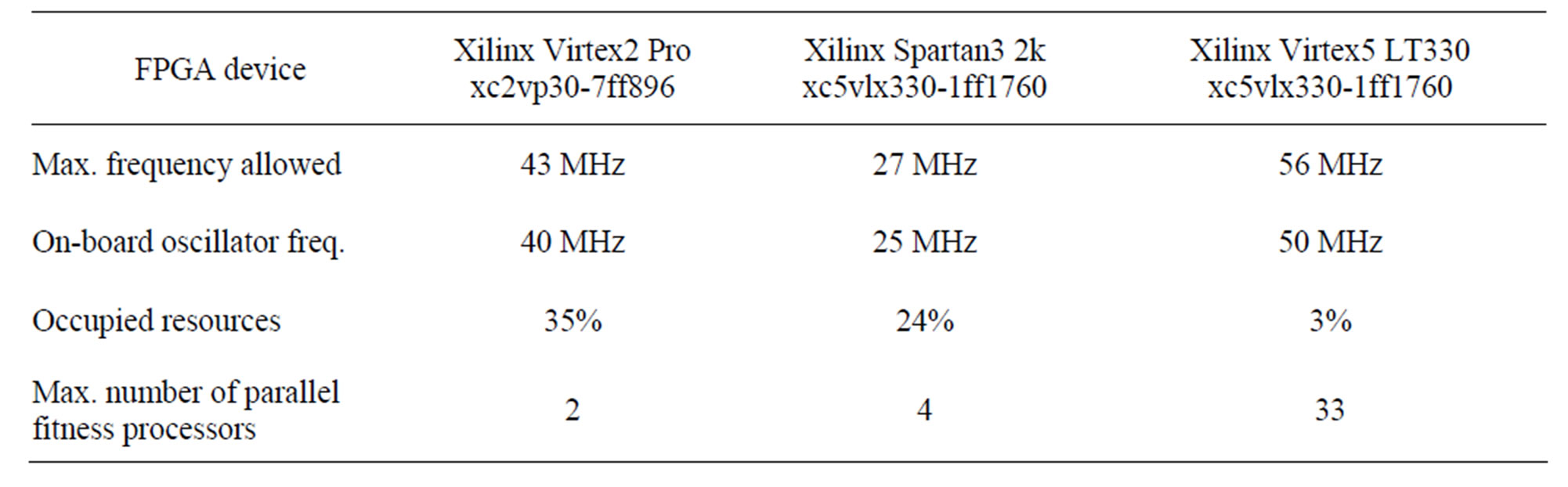
Table 2. Information related to the synthesis of the fitness processor.
in the memory so they could be read in order to validate their values. The processor guarantees accurate measures because it was designed following the IEEE 754 standard for the floating-point operations and the VHDL P1076 standard for the hardware description language. This accuracy was validated examining the fitness and coverage values stored in the on-chip memory.
3. Performance Study
We considered two additional terrain maps to analyze, that require different computational efforts:
• Map “mcity”. This concerns a real map, based on the city of Málaga, in Spain (Figure 6), where 1000 predefined localizations were determined for the placing of 100 antennas. The territory, of 4,25 km × 6,4 km, was codified into a network of 300 × 450 cells (135,000 points in the grid), where each one represents a terrain of approximately 15 m × 15 m. Taking into account the presence of the sea, mountains, public areas and other prohibited zones, the maximum possible coverage is 95.52%.
• Map “ccity”. This concerns a theoretical case where the computational cost is the highest: 724 × 724 grid points, with 2000 predefined available localizations for placing 300 antennas.
It is important to compare these hardware results with the ones obtained from custom software running on a general-purpose processor, in order to analyze the efficiency of the FPGA processor [14,15]. (We mention here that we do not know of any other FPGAor ASIC-based solution for the RND problem, with which to make a performance comparison). Thus, we have developed software (optimized to reach the maximum possible speed) for implementing the same operations as were performed on the FPGA. This software was run on different platforms (see Table 1) in order to make effective comparisons with the FPGAs of similar technologies and ages.
The result of the time analysis for both implementations (hardware and software) establishes the real performance and the effectiveness of the hardware implementation. In Figure 7 the summary of the time analysis is shown, for the test map (from this point onwards, all the results correspond to this case as representative of the different maps). Analyzing the graph we can see that the software solution is slightly better, due mainly by one reason: the FPGA processor design does not enclose a high level of parallelism in its arithmetical operations.
When considering the case of more than one fitness processor running in parallel, we calculate the maximum number of processors able to fit into the FPGA device, according to the reported occupied resources during the synthesis phase. In this case, in order to make a realistic

Figure 6. Map of high computational cost, codified with a 300 × 450 grid where 100 antennas must be placed on a predefined set of 1000 available locations. The shadowed areas show the maximum possible coverage.
comparison, the software version executes the 1000 iterations of the fitness function multiplied by the number of parallel processors in the FPGA device. The results of the new time analysis are shown in Figure 8. Analyzing the graphs we can see that the hardware solution is more advantageous in all the cases, especially for the newest FPGA.
4. Increasing the Performance
An increase in processor performance can be achieved by increasing the clock frequency of the overall operation of the circuit. This requires a set of timing closure techniques that include efficient design, synthesis adjustments, implementation constraints, etc. Using these techniques we can get a greater frequency but only by a small percentage.
The most effective way to increase significantly the performance of the hardware system is to distribute many parallel fitness processors in more than one FPGA device. The boards containing the FPGAs could be arranged in a cluster (Figure 9 shows two examples), using a master-slave based control system. Pursuing this idea, the performance increases in a linear manner.
For example, if we consider only two prototyping boards each containing a Xilinx Virtex5 LT330 device, we can put to work 33 processors in each one, so the whole system could have up to 66 fitness processors running in parallel. The computation times for the 1,000 fitness evaluations were 28 seconds for the fitness processor, and 21.78 seconds for the contemporary computer. The 66 fitness processors running in parallel spend the same 28 seconds, but the computer needs 21.78 seconds multiplied by 66, in other words, 24 minutes! We understand as performance the inverted computing time [15]. To compare the performance between FPGAs and CPUs,
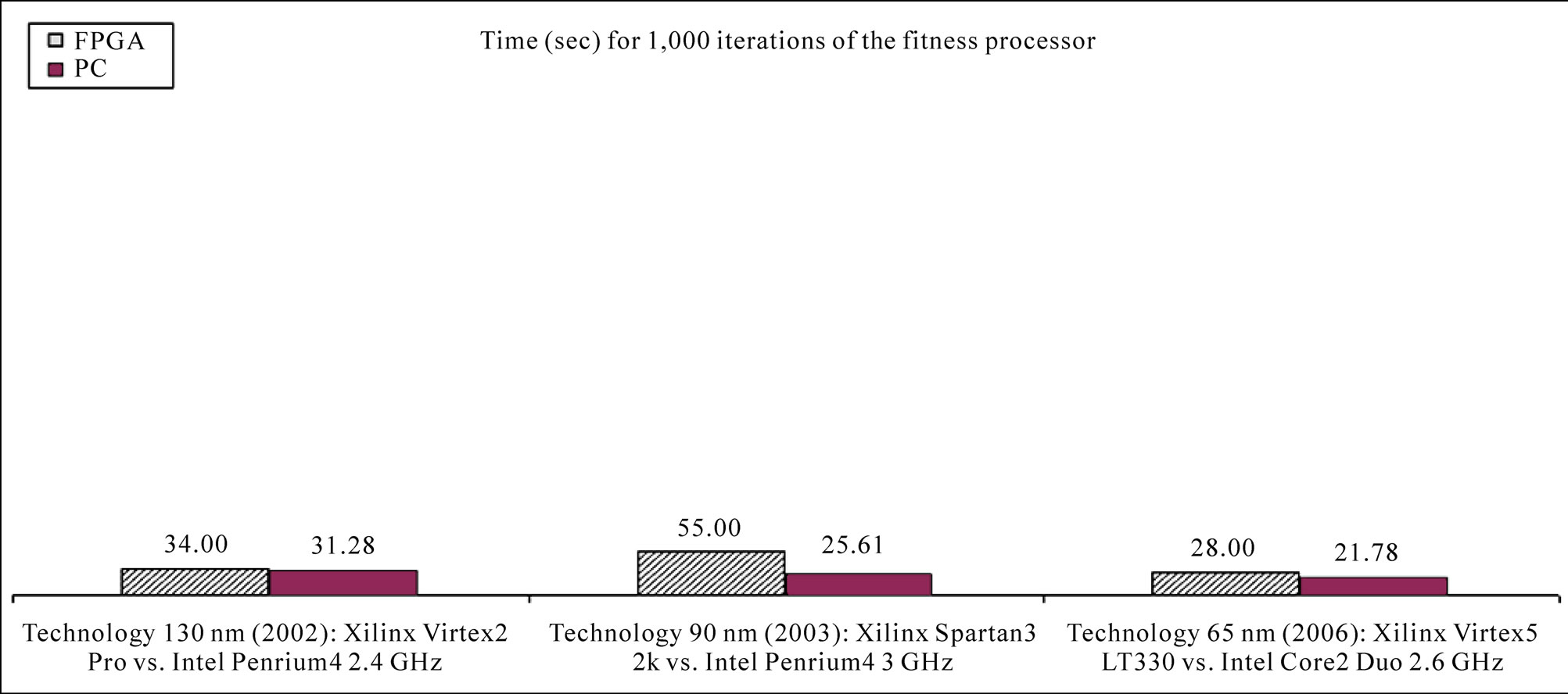
Figure 7. Computation times of 1000 evaluations of the fitness processor for the test map, obtained from different FPGA devices and general purpose computers.
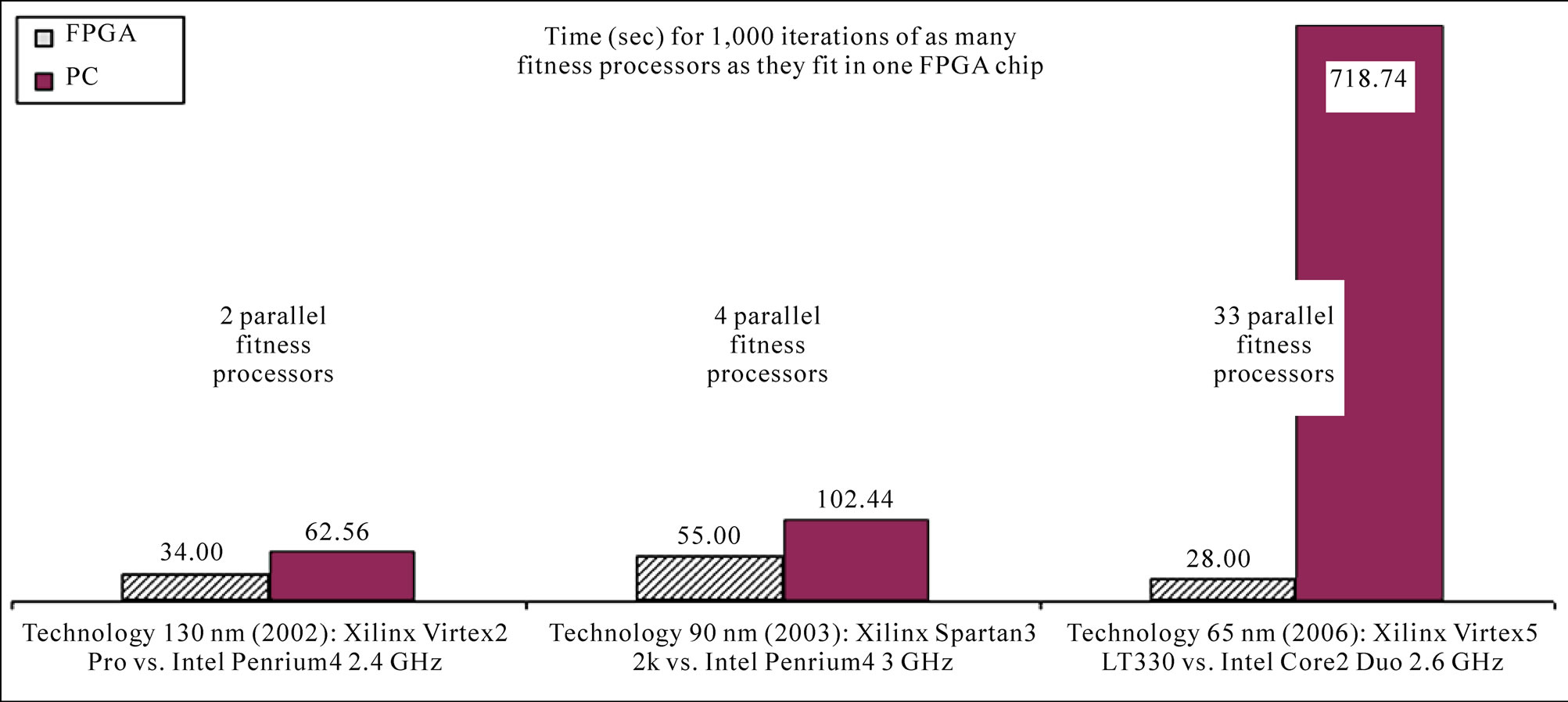
Figure 8. Computation times of some fitness processors working in parallel inside the FPGA, where each processor performs 1,000 fitness evaluations; the computer emulates the parallel calculus by multiplying the time for 1000 fitness evaluations by the specified number of reconfigurable processors.
we say that the FPGA is TCPU/TFPGA times faster than the CPU if TFPGA < TCPU. According to this definition, Figure 10 shows the large time improvement achieved in such clusters, using only two boards with only one FPGA device each board. The more boards we use, the more time improvement we will obtain, giving us unquestionable gains.
Taking into account the very low power consumption of the FPGA devices (less than 1 watt) in comparison to the general-purpose processors (around 100 watts), a FPGA cluster solution emerges as a very low-cost and very high-performance computing platform for running fitness processors in intensive computing scenarios.
5. Conclusions and Future Works
The interest of a hardware solution based on FPGAs to solve RND problems lies in the possibility of accelerating the calculations by means of the parallel processors working inside FPGA devices and the possibility of freeing computer resources, which otherwise would be

Figure 9. Two examples of clusters based on FPGA to compute parallel processors distributed in several devices.
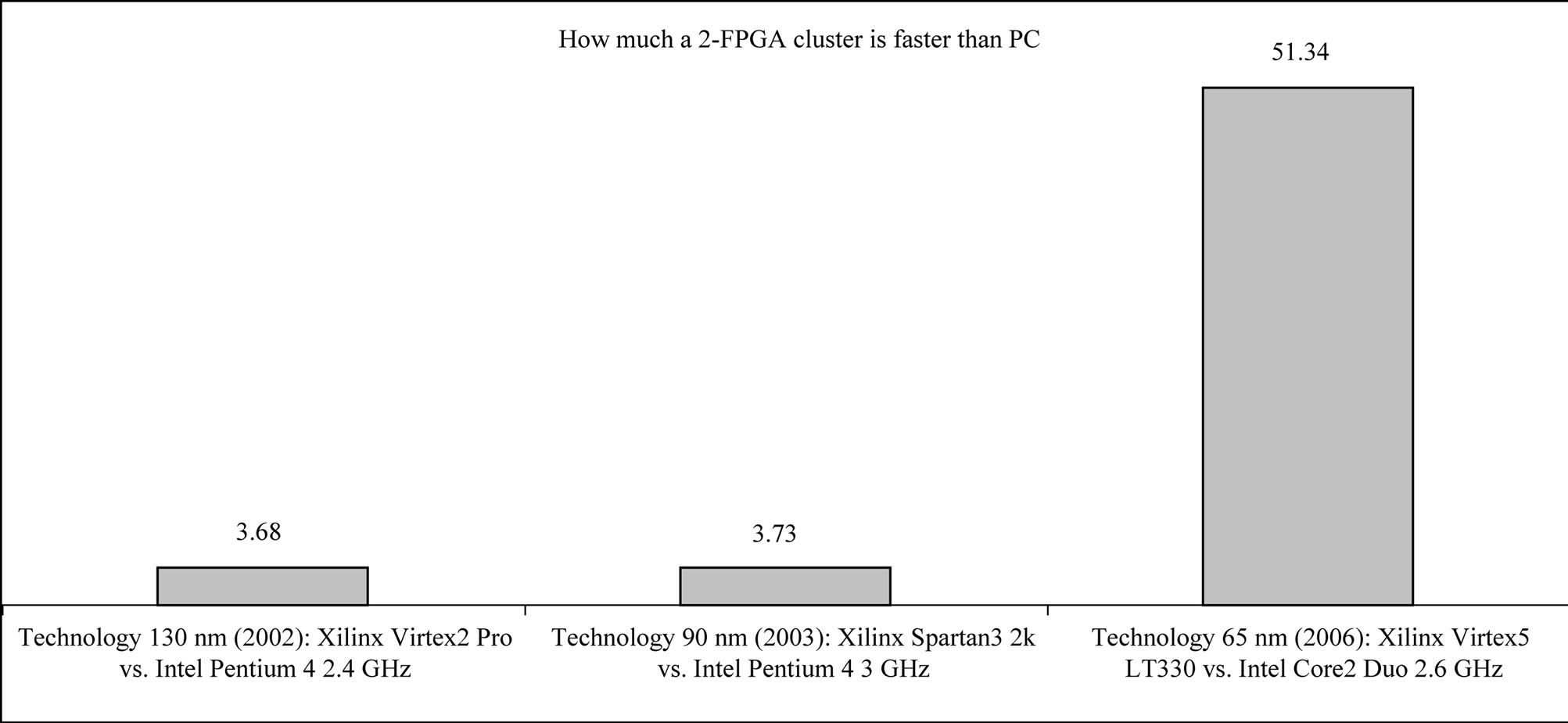
Figure 10. Time improvement; in other words, how much faster the FPGA cluster is compared to the computer.
dedicated almost exclusively to computing the solution to the problem over a great period of time and with a high cost in power consumption.
For this reason, the possibility of doing fitness processing by means of a specifically designed reconfigurable processor for evolutionary algorithms is sufficiently interesting to merit in-depth exploration of this computational alternative, which can offer better performance results clearly surpassing those of the computer.
One interesting future research line is to include the processor into an environment useful for designing real radio network deployments, where a practical combination of network simulators (such as NS-2 [16], to define cases of study) and evolutionary algorithms (to find their better solutions) would give the researchers the necessary tools for their works.
6. Acknowledgements
This work was partially funded by the Spanish Ministry of Science and Innovation and ERDF (the European Regional Development Fund), under the contract TIN2008- 06491-C04-04 (the MSTAR project).
REFERENCES
- P. Calegari, F. Guidec, P. Kuonen and D. Kobler, “Parallel Island-Based Genetic Algorithm for Radio Network Design,” Journal of Parallel and Distributed Computing, Vol. 47, No. 1, 1997, pp. 86-90. doi:10.1006/jpdc.1997.1397
- P. Calegari, F. Guidec and P. Kuonen, “Combinatorial Optimization Algorithms for Radio Network Planning,” Journal of Theoretical Computer Science, Vol. 263, No. 1-2, 2001, pp. 235-265. doi:10.1016/S0304-3975(00)00245-0
- E. Alba, “Evolutionary Algorithms for Optimal Placement of Antennae in Radio Network Design,” Proceedings of the 18th IEEE International Parallel and Distributed Processing Symposium, 26-30 April 2004, pp. 168- 174.
- S. Khuri and T. Chiu, “Heuristic Algorithms for the Terminal Assignment Problem,” Proceedings of ACM Symposium on Applied Computing, New York, 1997, pp. 245- 251. doi:10.1145/331697.331748
- E. Alba, “Parallel Metaheuristics: A New Class of Algorithms,” Wiley, New York, 2005. doi:10.1002/0471739383
- E. Alba and F. Chicano, “On the Behaviour of Parallel Genetic Algorithms for Optimal Placement of Antennae in Telecommunications,” International Journal of Foundations of Computer Science, Vol. 16, No. 2, 2005, pp. 86-90.
- S. Ivanov, A. Herms and G. Lukas, “Experimental Validation of the Ns-2 Wireless Model Using Simulation, Emulation, and Real Network,” Proceedings of the 4th Workshop on Mobile Ad-Hoc Networks, Bern, 26 February-2 March 2007, pp. 433-444.
- J. Laiho, A. Wacker, T. Novosad and A. Hämäläinen, “Verification of WCDMA Radio Network Planning Prediction Methods with Fully Dynamic Network Simulator,” Proceedings of the IEEE 54th Vehicular Technology, Vol. 1, 2001, pp. 526-530.
- S. Hauck and A. DeHon, “Reconfigurable Computing, the Theory and Practice of FPGA-Based Computation,” Morgan Kaufmann, San Fransisco, 2008.
- N. Nedjah and L. M. Mourelle, “Co-Design for System Acceleration: A Quantitative Approach,” Springer, Berlin, 2007.
- C. Maxfield, “The Design Warrior’s Guide to FPGAs: Devices, Tools and Flows,” Elsevier, Oxford, 2004.
- M. Gokhale and P. Graham, “Reconfigurable Computing: Accelerating Computation with Field-Programmable Gate Arrays,” Springer, Berlin, 2005.
- K. Ramamritham and K. Arya, “System Software for Embedded Applications,” Proceedings of the 17th IEEE International Conference on VLSI Design, 2004, pp. 12-14.
- K. Underwood and K. Hemmert, “Closing the Gap: CPU and FPGA Trends in Sustainable Floating-Point BLAS Performance,” Proceedings of the 12th IEEE Symposium on Field-Programmable Custom Computing Machines, 20-23 April 2004, pp. 219-228. doi:10.1109/FCCM.2004.21
- D. A. Patterson and J. L. Hennessy, “Computer Organization and Design—The Hardware/Software Interface,” Morgan Kaufmann, San Fransisco, 2009.
- T. Issariyakul and E. Hossain, “Introduction to Network Simulator NS2,” Springer, Berlin, 2008.

