Creative Education
Vol.5 No.11(2014), Article
ID:47178,6
pages
DOI:10.4236/ce.2014.511110
Solving Equations with Parameters
Bat-Sheva Ilany1, Dina Hassidov2
1Beit-Berl College, Kfar Saba, Israel
2Western Galilee College, Akko, Israel
Email: bat77i@gmail.com, hasidov@netvision.net.il
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()


Received 23 April 2014; revised 16 May 2014; accepted 6 June 2014
ABSTRACT
This study examines how high school pupils and student teachers tackle equations that are presented in various ways. Some presentations are non-standard, for example having to express “a” (usually perceived as a parameter) in terms of “x” (usually perceived as a variable). We investigate how subjects solve those equations as well as the differences between pupils and student teachers. Our findings suggest that equations containing parameters are more difficult to solve than equations without parameters. The difficulties are associated with the letters that should be expressed and in the arrangement of the equation. The results of this study may expand the knowledge of teachers on the subject of equations with parameters and on the specific difficulties encountered by students during the solution process.
Keywords:Equations, Parameters, High School Pupils, Student Teachers, Mathematics Education, Mathematics Knowledge, Cognition and Mathematics

1. Theoretical Framework
“Problems with parameters test the solver’s knowledge of mathematics deeply and detect his weak points” (Sedivy, 1976). Sedivy also claims that pupils encounter more difficulties with equations with parameters than with numerical coefficient equations. Algebraic equations containing parameters represent larger classes of equations and more general forms of quantitative relationships compared to equations without parameters.
Davis & Henkin (1978) wrote on the importance of quadratic equations in general and with parametric coefficients in particular. They describe how they interpret understanding of quadratic equations. They provide a long list of skills as well as the mathematical knowledge which are required in order to understand and solve quadratic equations. Davis and Henkin argue that understanding and solving equations with parameters improve students’ understanding of equations in general.
Skemp (1987) argues that learning rules without reasons allows the pupil to function only within a narrow framework, and to deal merely with standard problems. However, this approach limits the students’ understanding and they would not be able to cope with more complex tasks. Understanding enables the pupil to handle non-standard problems which cannot be solved by mechanical application of formulas. Fischbein and Muzicant (2002) indicate that pupils learned primarily in procedural manner and that hence they often fail to distinguish between conceptual and procedural knowledge. Many pupils find it difficult to recognize that a letter represents a number and do not know how to work with symbolic values (Kieran, 1992, 2014).
It is widely agreed that it is important for teachers to recognize how their students perceive the mathematical topics, in particular the specific reasons for making errors (Almog & Ilany, 2012).
In elementary courses students get used to x (and later on y and z) being variables, and letters such as a, b, c being constants or parameters. However, in more advanced courses they come across questions where the letters are used differently, and they find it very confusing. For example, integration problems where x is fixed and y is the variable. Or volume questions where a, b, c are used as variables.
Pupils solve at school countless exercises of equations in which the letter x represents a variable that should be expressed in terms of the letters a, b, c etc… In this study, subjects were given a variety of equations with non-standard presentation, as mentioned above.
2. Purpose
The study objectives are to examine and identify the difficulties of high school pupils and pre-service student teachers in solving equations with parameters. In addition, to find out if there are significant differences between pupils and student teachers in regards to solving such equations. Which procedures are used and which difficulties are encountered in solving equations with parameters.
3. Research Questions
1) How do the subjects solve equations with parameters where they have to express various letters in terms of other letters and parameters? In particular when the equations are not arranged in a standard manner.
2) Are there differences between pupils and student teachers in regards to the way they solve such equations. And if so, what are the differences.
Examples of equations investigated in the article (the numbering of the questions follows that of the questionnaire):
• Question 16: Find x (in terms of a) in 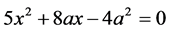 (fairly standard equation, with variable x and parameter a).
(fairly standard equation, with variable x and parameter a).
• Question 1: Find c (in terms of x) in  (less standard as it is required to express c in terms of x).
(less standard as it is required to express c in terms of x).
• Question 9: Find b (in terms of x) in 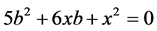 (less standard as it is enquired to rearrange the equation “properly” and then to express b in terms of x).
(less standard as it is enquired to rearrange the equation “properly” and then to express b in terms of x).
• Question 21: The following equation is linear in x, though might mistakenly appear to be a quadratic equation in terms of a:![]() .
.
We refer to the necessary knowledge needed for solving simple equations as a procedural knowledge. Equations with non-standard presentations call for more flexible approach.
4. Method
The study sample consisted of 115 mathematics student teachers in their third and fourth year of studies, and 133 twelfth grade pupils of high mathematics level (5 unit mathematics stream) in four secondary schools.
Instruments: A questionnaire was designed for the study and administered to both groups. Part of the questionnaire consists of six questions which include equations with parameters. This study reports the findings of two questions of first degree equations (questions (5) and (21)) and three questions of second degree equations (questions 16, 1 and 9). The questions are listed in Table 1 and Table3
Procedure: To understand the subjects’ solution process, five pupils and six student teachers were interviewed. The interview questions were designed after the questionnaire was filled out and analysed. The purpose was to clarify and prod further the findings of the questionnaire. In addition, open observations were made in order to examine closely the subjects’ responses.
Table 1. Questions 5 and 21, analysis of the results (first degree equations with parameters).
Note: (P = Pupils, S.T. = Student Teachers). *The subjects expressed x correctly but some of them failed to specify valid domain and then to simplify the expression. See Table 2 for details.
Data Analysis: Quantitative analysis was carried out via descriptive statistics (tables that list percentage of success), c2 tests and t-tests. Qualitative analysis was carried out by observations and interviews as mentioned above. The results were then analysed according to the emerging criteria.
5. Results
The results of the first degree equations5 and 21 are presented in Table1
Table 1 shows that a large percentage of high school pupils (22%) did not answer question 21. A very small percentage of the subjects who expressed correctly x in terms of a also specified the correct domain of the solution. Some of the subjects coped only with standard questions which required straightforward approach. Overall, only 36% of pupils and 73% of the student teachers gave a complete solution to question 21.
In question 5, subjects were asked to express the letter min terms of x. m is a letter that is usually perceived as a parameter (Ilany, 1997, 1998). In this question we have a first degree equation for which the solution process should be simple, but only 67% of pupils gave the correct answer and 29% erred. We posit that the mistakes stem from the confusion associated with non-standard use of parameters and variables (Examples are given below). For the student teachers the situation was better, 88% solved correctly and 10% made errors associated with the non-standard presentation.
In question 21, the equation ![]() is of first degree in x and x had to be expressed in terms of a. This presentation of the equation was associated with various mistakes in the solution process of the subjects as x is usually perceived as a variable (Ilany, 1997). It is worth noting that equation 21 is actually linear in x, as x is the variable of degree one. However, due to the a2 in the equation, some students were confused and perceived the equation as quadratic.
is of first degree in x and x had to be expressed in terms of a. This presentation of the equation was associated with various mistakes in the solution process of the subjects as x is usually perceived as a variable (Ilany, 1997). It is worth noting that equation 21 is actually linear in x, as x is the variable of degree one. However, due to the a2 in the equation, some students were confused and perceived the equation as quadratic.
In order to solve the above equation it is required to open parenthesis, gather similar expressions and rearrange the equation. There is a restriction on a (a ≠ −1), and several algebraic operations are required to solve the equation. Numerous mistakes were made by the subjects who attempted to solve this question, especially the pupils. Only 36% of the pupils expressed x in terms of a correctly. That is, they found that:
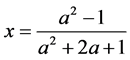
However, most of the students who expressed x correctly failed to specify the valid domain and to simplify the resulting equation (see Table 2).
For the student teachers, the situation was better: 73% of them answered question 21 correctly. An analysis of the errors revealed that 41% of pupils compared to 14% of student-teachers made errors associated with the “non-standard” letters (see Table 1).
We chose to explore three second degree equations in this study. In each equation it is required to express a given letter by another one. Errors were divided into two types: mistakes in calculation and errors resulting from confusion associated with the non-familiar usage of letters: ignoring letters, finding the wrong letter and circular expression of letters. (Examples will be cited in Table 3: questions 16, 1, and 9).
According to Table 3, high percentage of pupils (16%) did not answer question 9. There was a significant difference between student teachers and high school pupils in all of the three questions. The three equations have a similar structure (Table 3). The difference between them is that in question 16 (5x2 + 8ax + 4a2 = 0), x has to be found, a letter perceived as a variable according to Ilany (1997, 1998), while in the other equations the
Table 2 . Question 21—Subjects who expressed x correctly, (some of them did not complete the process).
Note: (P=Pupils, S.T. = Student Teachers).
Table 3. Questions 16, 1, and 9, analysis of the results.
Note: (P = Pupils, S.T. = Student Teachers).
letters that should be found are b or c. These letters are usually perceived as parameters, hence they caused confusion.
The results show that more students answered question 16 correctly compared to questions 1 and 9 (see Table 3), which addresses Research Question 1. (That is, that solvers tend to get confused when required to express a, b, c or m (normally function as parameters) in terms of x (which usually stands for a variable).
A significant difference was found between student teachers and pupils in two respects. To begin with, the student teachers scored better on all questions. In addition, a smaller proportion of student teachers seems to have been confused by the change and rearrangement of variables (70% of pupils answered question 16 correctly versus 28% for question 9; the corresponding figures for student teachers are 88% vs. 43%).
Table 3 presents three questions of similar structure. The first question (16) is fairly standard (Expressing x in terms of other parameters).
In the second question (1), we have a non-standard use of letters (expressing x in terms of c).
The third question also involves a non-standard use of variables, as b has to be expressed in terms of x. Moreover, you have to rearrange the equation in order to solve it.
Comparing the results of questions 9 and 1 highlights the significance of the arrangement of the equation. In question 9 the equation (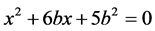 ) resembles the equation in question 1 (
) resembles the equation in question 1 (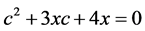 ), but is not arranged in the usual order, that is, higher exponents written first. Here we received the lowest results (only 28% of pupils and 43% of student teachers solved the equation correctly). The reasons for these results are attributed to the difficulty in arranging the equation and finding the non-standard letter b in terms of x.
), but is not arranged in the usual order, that is, higher exponents written first. Here we received the lowest results (only 28% of pupils and 43% of student teachers solved the equation correctly). The reasons for these results are attributed to the difficulty in arranging the equation and finding the non-standard letter b in terms of x.
Question 1 was also discussed in the interview. The interviewer emphasized that b or c has to be expressed in terms of x. In spite of this fact most respondents expressed x in terms of b or c. One interviewee that made that mistake said: ”Even though you do not want x, you want b, I automatically find x, because this is a quadratic equation”. She made an attempt to express b saying: “I cannot find b, I know that there are two solutions because D > 0, but I cannot find it, I think that it is impossible”. At the end of the interview, we went back to the question. This time we rearranged the equation as: , and the interviewee expressed b in terms of x without any difficulty. In other words, it was difficult for the student to even start the solution process when faced with non-standard arrangement and letters, although she had no technical difficulty solving such equations once rearranged properly. The same student teacher managed to rearrange and successfully solve an “untidy” equation where x had to be expressed in terms of b, that is, standard use of letters. After the interview she said:”From now on I will ask my pupils to express different letters, not necessarily in the usual order”.
, and the interviewee expressed b in terms of x without any difficulty. In other words, it was difficult for the student to even start the solution process when faced with non-standard arrangement and letters, although she had no technical difficulty solving such equations once rearranged properly. The same student teacher managed to rearrange and successfully solve an “untidy” equation where x had to be expressed in terms of b, that is, standard use of letters. After the interview she said:”From now on I will ask my pupils to express different letters, not necessarily in the usual order”.
It is interesting to note that rearranging the equation in question 9 is one way to solve it. Another way is to interchange letters, that is, to swap x and b, solve for x, then swap the letters again. None of the subjects applied this method.
Examples of errors resulting from using non-standard letters in the above questions:
In question 1 the correct answer is: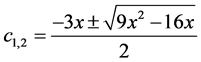 . In this case it was difficult for some participants to accept an “unfinished solution”, even though this expression cannot be simplified further, except that the domain ought to be specified.
. In this case it was difficult for some participants to accept an “unfinished solution”, even though this expression cannot be simplified further, except that the domain ought to be specified.
Consequently, some subjects who solved the question correctly were not satisfied with their answer and crossed it. However, we did consider the crossed solutions to be correct.
A related mistake was expressing x instead of c (2% of student teachers).
“You cannot find c as it is a parameter” (5% of student teachers).
“c is a parameter and therefore can be any number.”
An interesting error in question 16 was getting the correct answers then omitting “a” from those answers. That is, the student wrote:
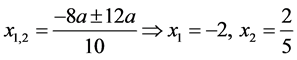
A similar mistake was mixing up “x” and “a”:
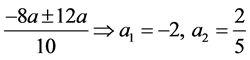
Examples of errors in question 9: Finding x instead of b (11% of pupils, 5% of student teachers).
Expressing b in terms of b. (6% of pupils, 10% of student teachers):
Similarly, in question 21, 4% of the high school students expressed x in terms of x, for example:
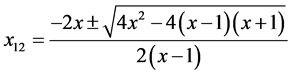
Examples of mistakes that took place while attempting to solve:
![]()
“Impossible to express x on its own.”
“Don’t know” (32% of students, 5% of student teachers).
Turn x into x2 (6% of students, 2% of student teachers).
Expressed a instead of x (3% of students).
Examples of mistakes that took place while attempting to solve question 5: Find m in: 
Found x (3% of students).
“Impossible” (10% of students, 7% of student teachers).
Turned the equation into a quadratic equation for m (3% of students).
6. Discussion
The results of this study indicate that for equations with parameters, a large percentage of student teachers, and even larger proportion of pupils, erred due to confusion associated with non-standard use of letters, (for example, having to express a in terms of x). Being faced with equations where the parameters and variables were not arranged in a standard manner made it even more difficult for the subjects to solve those equations.
In general, equations containing parameters are more difficult to solve than equations without parameters. Subjects tend to solve equations mechanically, and hence they make numerous mistakes when they come across non-standard questions which call for deeper understanding.
Key factors that are often problematic for students are the type of the letter that has to be expressed, the arrangement of the equation to be solved, the power of the variable, the power of the parameter and the type of the algebraic techniques required.
Implications for teaching how to solve equations with parameters The findings of this study, in particular the large number of mistakes, raise questions in regards to the efficacy of the teaching of this topic. Hence, in order to improve students’ understanding of equations with parameters, it is recommended to improve students’ understanding concerning the use of letters in such equations. For example, by careful reading of what is required in the question, by adopting a more flexible approach in regards to which letters can be expressed in terms of other letters, by making sure that the expression is simplified properly, and by being aware of the differences and similarities between equations with or without parameters.
We recommend including in the school mathematics curriculum more equations with various parameters and variables, as well as equations which are not presented in the usual order. Doing so will encourage students to think more deeply about the topic and to gain deeper understanding.
References
- Almog, N., & Ilany, B.-S. (2012). Absolute Value Inequalities: High School Students’ Solutions and Misconceptions. Educational Studies in Mathematics, 81, 347-364. http://dx.doi.org/10.1007/s10649-012-9404-z
- Davis, R. B., & Henkin, L. (1978). Inadequately Tested Aspects of Mathematics Learning—Testing, Teaching and Learning. Report of a Conference on Research on Testing, National Institute of Education, 49-63.
- Fischbein, E., & Muzicant, B. (2002). Richard Skemp and His Conception of Relational and Instrumental Understanding: Open Sentences and Open Phrases. In D. Tall, & M. Thomas (Eds.), Intelligence, Learning and Understanding in Mathematics: A Tribute to Richard Skemp (pp. 49-77). Flaxton, QLD: Post Pressed Publishers.
- Ilany, B. (1998). The Elusive Parameter. In The 23rd Annual Meeting of the International Group for the Psychology of Mathematics Education (Vol. 4, p. 265). Stellenbosch: University of Stellenbosch.
- Ilany, B. (1997). The Concepts of Variable and Parameter of Pre-Service Teachers and High School Students. Doctoral Dissertation, Tel Aviv: Tel Aviv University. (in Hebrew)
- Kieran, C. (1992). The Learning and Teaching of School Algebra. In D. A. Grouws (Ed.), Handbook of Research on Mathematics Teaching and Learning (pp. 390-419).
- Kieran, C. (2014). Algebra Teaching and Learning. Encyclopedia of Mathematics Education (pp. 27-32). Springer: Springer Reference.
- Sedivy, J. (1976). A Note on the Role of Parameters in Mathematics Teaching. Educational Studies in Mathematics, 7, 121-126. http://dx.doi.org/10.1007/BF00144365
- Skemp, R. (1987). The Psychology of Learning Mathematics. Hillsdale, NJ: Lawrence Erlbaum Associates.


