Journal of Sustainable Bioenergy Systems
Vol.3 No.1(2013), Article ID:29579,7 pages DOI:10.4236/jsbs.2013.31012
Numerical Simulation of Partial Combustion for Biomass Tar Elimination in Two-Stage Gasifier
Institute of Thermal Energy Engineering, Shanghai Jiao Tong University, Shanghai, China
Email: *yhluo@sjtu.edu.cn
Received February 2, 2013; revised March 5, 2013; accepted March 15, 2013
Keywords: Biomass Tar; Partial Combustion; Numerical; ER
ABSTRACT
Biomass tar is an obstacle in biomass gasification. Partial combustion is a potential method for tar elimination. To better study the tar conversion conditions and design reasonable partial combustion reactor, 2D/3D throat models are establish to calculate the tar reduction during partial combustion using numerical method. Different number of nozzles, injection directions and injection velocities were investigated. SIMPLE algorithm was used in this calculation. The results indicated that the best performance of partial combustion was obtained when ER (equivalent ratio) = 0.34. A performance of 3 nozzles, perpendicular injection and 20 m/s injection velocity could reach lowest tar content of 3.09 wt%.
1. Introduction
Biomass gasification is a potential way for the usage of biomass energy. Tar contained in the fuel gas is the main obstacle for the usage of biomass widely. There are quite a lot of methods to reduce tar content [1]. Considering the economy and environment-friendly, Partial oxidative/ (combustion) is a attracting way , for it’s no need for expensive mechanical equipment and can lead to a very high tar reduction. Partial combustion is kind of combustion process that ER is no more than 1. Some scholars have conducted a series of research on this area. Brandt et al. [2] did some work on a 100-kW two-stage gasifier, and the tar content after char bed could be as low as 10 - 40 mg/kg dry wood. X. Guo et al. [3] did research on air-steam gasification of biomass micron fuel (BMF) in a cyclone gasifier. The experimental results showed that the gasification performance was best with ER being 0.37 and S/B being 0.31. Two-stage downdraft gasifier is a kind of low-tar method for biomass conversion. The throat in the gasifier is a crucial part for tar elimination.
The design of throat and choice of reaction condition is crucial. Numerical calculation is a good way to solve this problem, for it’s cheap and high efficient [4]. But there are still very few researches on this area especially on the designing of the throat for partial combustion of biomass tar. This paper gives a detail simulation that will optimize the operation of gasification and the designing of gasifier. A 2D laminar flow reaction was calculated and compared to experiment results to test and verify our model. 3D model of throat combustion area was established to optimize partial oxidation for tar destruction.
2. The Physics and Mathematic Model
Partial combustion is a complex process that contains several parts: fluid flow, mass transfer, heat transfer and chemical reaction. These four parts couple with each other in a particular reactor and it’s nearly impossible to obtain its analytic solution. Numerical calculation is a considerable method to solve it. To use numerical calculation, we first need to establish the physic and mathematic model.
2.1. Flow and Heat Transfer
Fluid flow equations:
 (GE-1)
(GE-1)
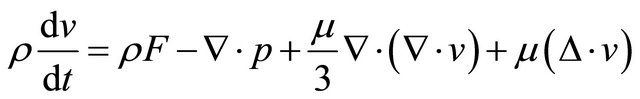 (GE-2)
(GE-2)
Heat transfer equation:
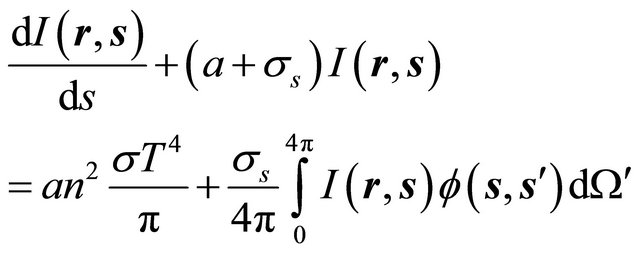 (GE-3)
(GE-3)
Turbulence k-e equation:
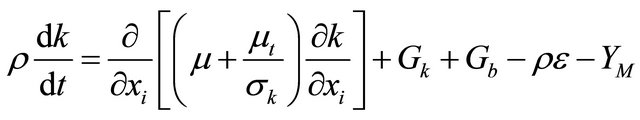 (GE-4)
(GE-4)
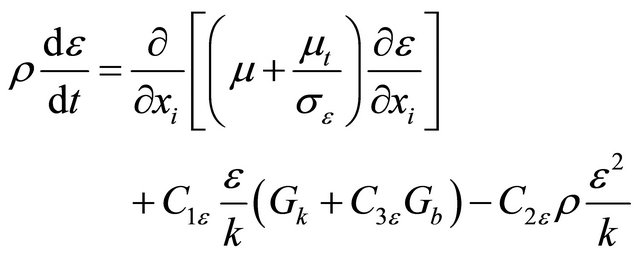 (GE-5)
(GE-5)
Special transport reaction:
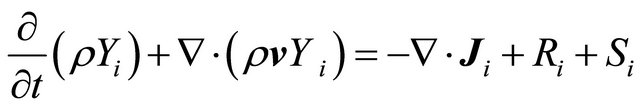 (GE-6)
(GE-6)
 (GE-7)
(GE-7)
2.2. Chemical Mechanism
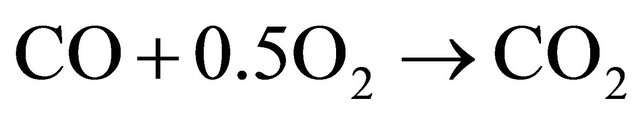 (1)
(1)
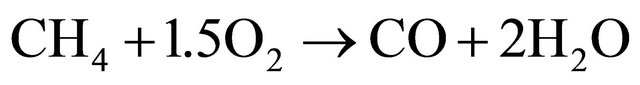 (2)
(2)
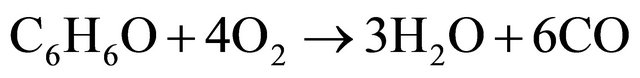 (3)
(3)
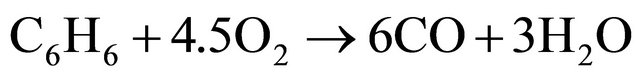 (4)
(4)
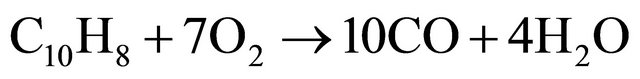 (5)
(5)
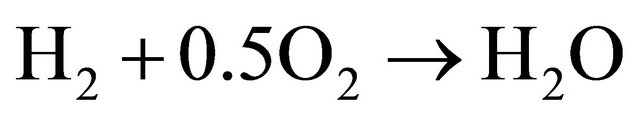 (6)
(6)
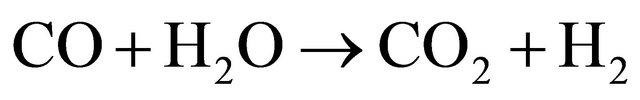 (7)
(7)
 (8)
(8)
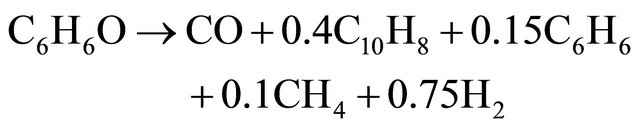 (9)
(9)
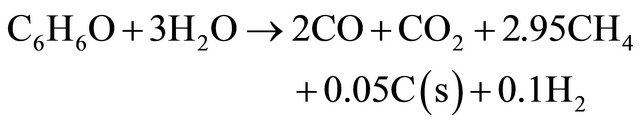 (10)
(10)
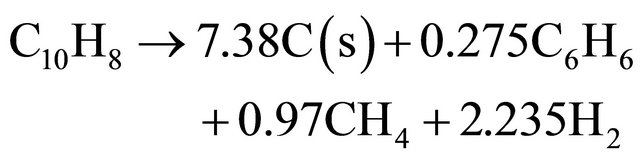 (11)
(11)
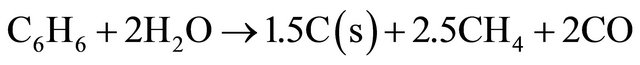 (12)
(12)
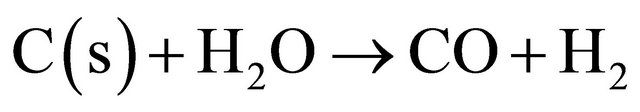 (13)
(13)
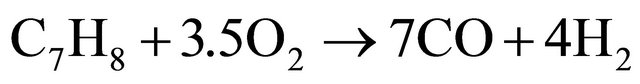 (14)
(14)
 (15)
(15)
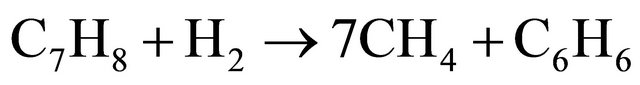 (16)
(16)
Table 1 is the kinetic parameters used in this model. All this parameters are from references.
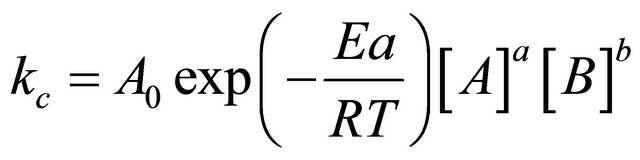 (17)
(17)
Arrhenius reaction rate was calculated from Equation (17).
2.3. Boundary Condition and Solutions
Commercial CFD software FLUENT was used to stimulate this model. Standard 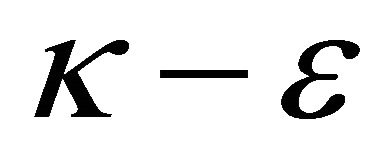 model was chosen to calculate turbulent flow. SIMPLE (Semi-Implicit Method for Pressure Linked Equations) algorithm couples velocity and pressure. EDC model can couple turbulent flow and chemical reaction very precisely. Total mesh grid is
model was chosen to calculate turbulent flow. SIMPLE (Semi-Implicit Method for Pressure Linked Equations) algorithm couples velocity and pressure. EDC model can couple turbulent flow and chemical reaction very precisely. Total mesh grid is
Table 1. Kinetic constants used in this model.
about 30,000 and mesh dependence test has been conducted. Calculation was done on a 3.0 GHz computer for 10 hours.
Verification mechanism experiments were conducted on the Laminar flow reactor in Biomass Research Center in SJTU as introduced in our formal works [15].
Figure 1 shows the boundary of the reactor. Boundary conditions: As phenol is the main pyrolysis products of wood, we choose phenol as the tar. Composition and flow rate of the inlet gases: C6H6O (0.45478), CO (0.0303), CO2 (0.14078), CH4 (0.0063), H2 (0.00037), H2O (0.36747); Inlet temperature: 500˚C, Inlet turbulence intensity: 10%, Inlet turbulence length: 0.035 m, Air inlet temperature: 27˚C, Wall temperature: 900˚C.
3. Results and Analysis
3.1. Mechanism Verification Model
This part was to test and verify our model in a Pipe flow reactor. Compared to the experiments in different conditions (ER = 0, 0.029, 0.1, 0.153, 0.2, 0.278, 0.34, 0.4), we can have a clear idea whether this model is reasonable and optimize the ER for our next research.
Figure 2 shows that the temperature increases with the increase of ER. Partial oxidation is an exothermal process. The more oxygen, the more sufficient the reaction will be. But more oxygen will decrease the calorific value of product gas. At the same time, temperature distribution may have an influence on the soot production because high temperature without oxygen may lead PAHs converted into soot.
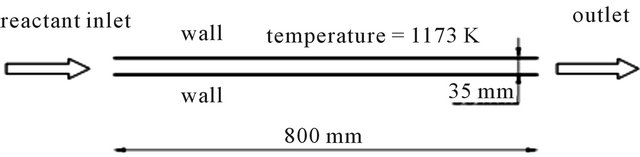
Figure 1. Geometry scale.

ER = 0.029 ER = 0.153
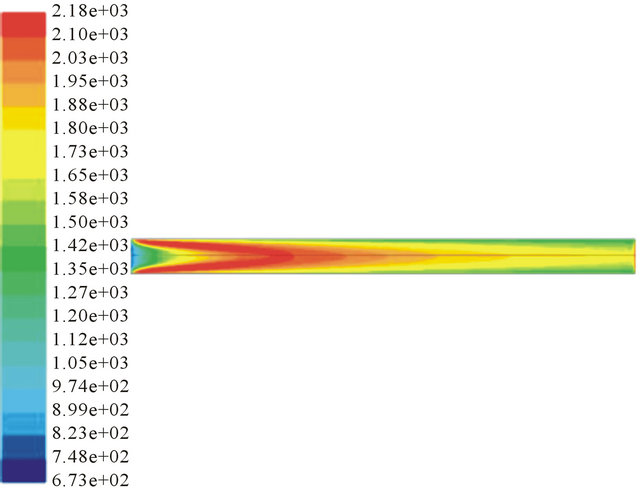
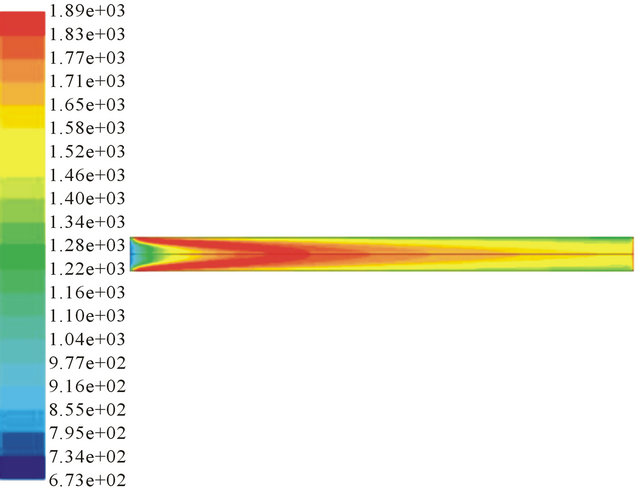
ER = 0.34 ER = 0.4
Figure 2. Temperature profile in different ER condition.
Figure 3 shows that the soot production can reach a lowest level when ER = 0.34 in the experiment. Figure 4 shows that the flow rate of total tar in modeling agrees with the experimental results conducted in the plunger flow reactor generally. The experimental result is lower than the modeling results. The reason is that the tar produced in the experiment cannot be collected very completely, especially in the case that the tar production is large.
Experiment and modeling results show that the partial oxidation can achieve an optimal effect when ER = 0.34. In our later research, we choose ER = 0.34 as the unified air injected.
3.2. The Design and Modeling of Throat Partial Combustion
The design of combustion room for partial oxidative is very important. The different styles of air velocities, the injection directions and the number of air nozzles can lead to the different mixability of gases, the residual

Figure 3. Effect of ER on soot.

Figure 4. Flow rate of total tar in modeling and experimental results (kg/h).
times, and the temperature distribution. In the follow part, we’ll model several of these influencing factors and guide the operation and design of real gasifier.
The inlet gases composition is the same as the 2D model.
Figure 5 shows the 3D geometry model of the throat part. The structured grid is composed of 113,000 cells. Meshing test has been conducted. There is nearly no difference when grid cells are more than 110,000. Calculation was done on a 3.0 GHz computer for 36 hours.
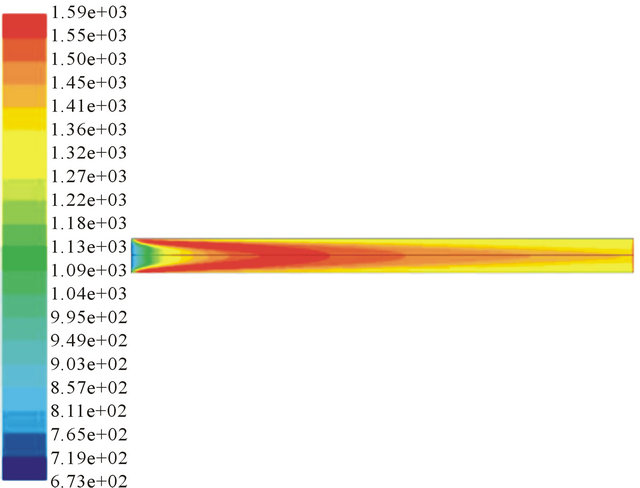
Figure 6 shows that 3 air nozzles can create highest temperature in the throat. The temperature is as high as 2030 K and the high-temperature area is the largest. High temperature benefits for the conversion of biomass tar. The counter flow and eddies in the throat can mix reactants fully and improve the residence time.
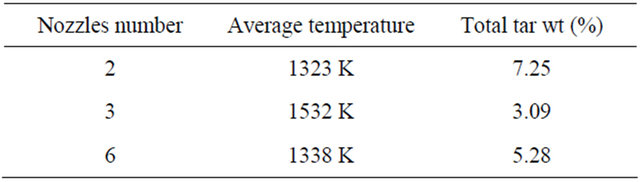
Table 2 shows the average temperature and total tar content in the outlet of the throat with different nozzle number. The tar quantity in outlet of throat reaches the lowest level when the nozzle is 3. As analyzed before, high temperature and mixing effect are the main effects on the tar conversion.
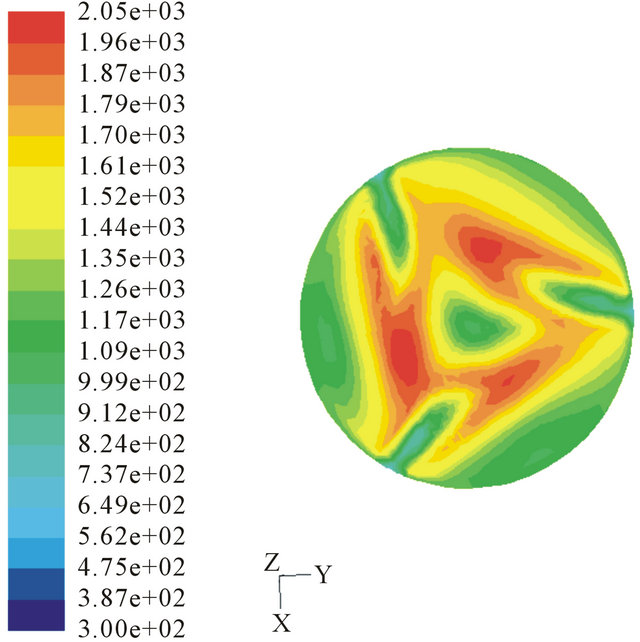
We choose injection angers as 15˚, 30˚ and 60˚ to calculate. The temperature profiles are shown in Figure 7. The tar quality in the outlet is 3.54%, 3.82% and 7.63% separately. And compared to perpendicular injection (3.09%), we can confirm that the annular combustion can’t benefit the tar conversion. Because annular combustion will lead to form cold channel to bypass tar gas and the counter flow up the throat is weaken largely. Different velocities of the injection air are also learned. Velocities of 10 m/s and 20 m/s were chosen to simulate
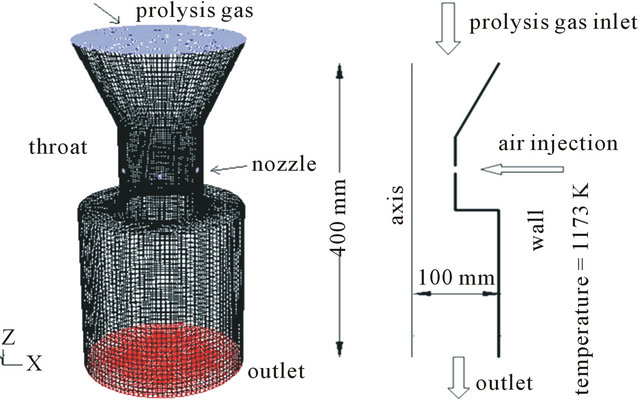
Figure 5. Computational geometry model.
Table 2. Highest temperature and tar quantity in outlet.
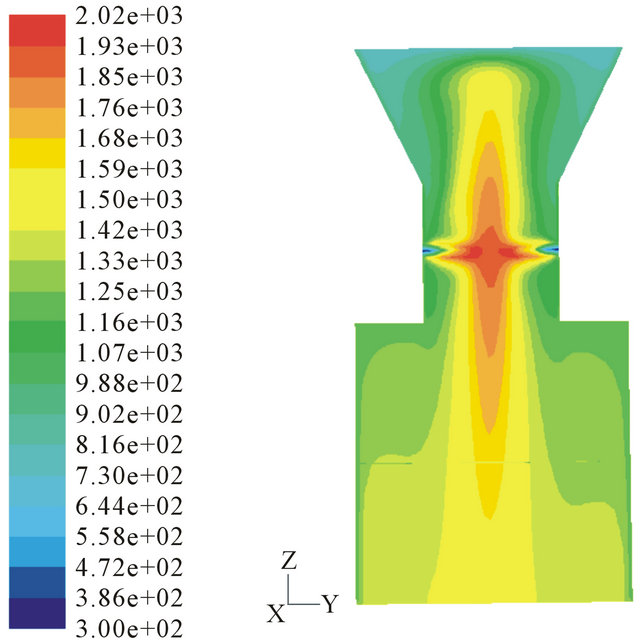 (a)
(a)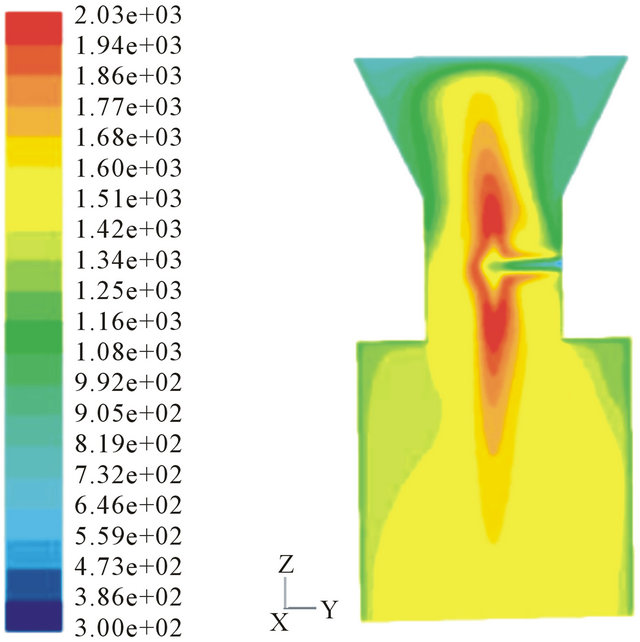 (b)
(b)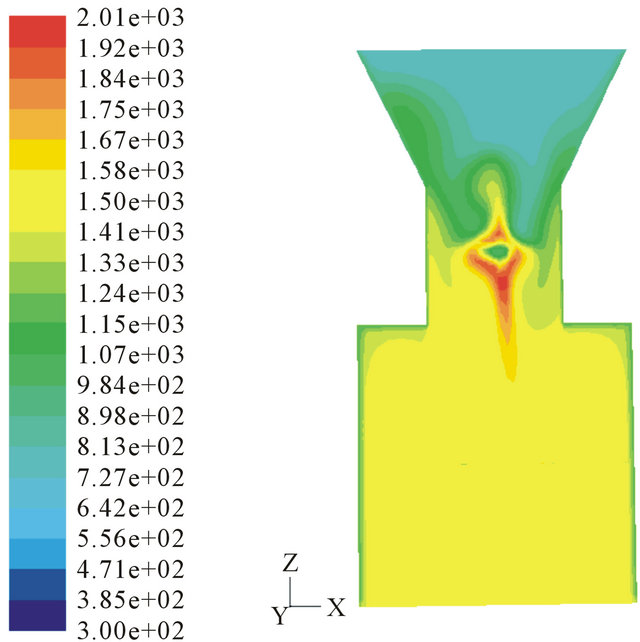 (c)
(c)
Figure 6. Temperature profile in different air nozzles. (a) 6 air nozzles; (b) 3 air nozzles; (c) 2 air nozzles;
 (a)
(a)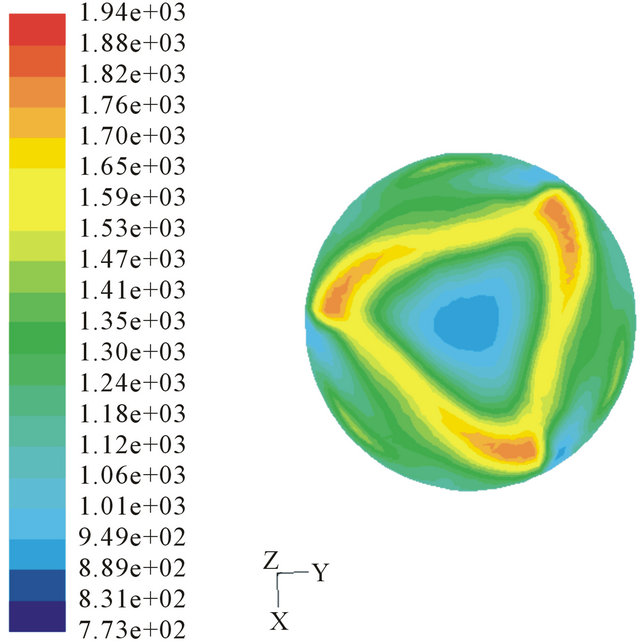 (b)
(b)
Figure 7. Temperature profile of different inject angles. (a) 15˚ injected; (b) 30˚ injected.
the combustion. The tar quality in the outlet is 3.24% and 3.09% separately.
4. Conclusion
The performance of partial combustion for tar conversion was investigated both by experiment and numerical method. In the laminar flow reactor, different ER values were modeled. Experiments and numerical calculation both confirmed that ER = 0.34 was an optimized value for tar conversion. Different number of nozzles, injection angles and injection velocities were investigated by CFD software in the design of real combustion throat for tar conversion. Results showed that 3 nozzles, perpendicular injection and injection velocity of 20 m/s performed best and reached the lowest tar content in outlet of throat. Method and Results from this numerical simulation may be useful for development of a real partial combustion throat in the future.
5. Acknowledgements
The authors are grateful to the Science and Technology Commission of Shanghai Municipality for its financial support (under Grant 05dzl2010) and appreciate the financial support of National Nature Science Foundation of China (51176120/E0607)
REFERENCES
- S. Anis and Z. A. Zainal, “Tar Reduction in Biomass Producer Gas via Mechanical, Catalytic and Thermal Methods: A Review,” Renewable and Sustainable Energy Reviews, Vol. 15, No. 5, 2011, pp. 2355-2377. doi:10.1016/j.rser.2011.02.018
- P. Brandt, E. Larsen and U. Henriksen, “High Tar Reduction in a Two-Stage Gasifier,” Energy & Fuels, Vol. 14, No. 4, 2011, pp. 816-819.
- X. J. Guo, B. Xiao, X. L. Zhang, S. Y. Luo and M. Y. He, “Experimental Study on Air-Stream Gasification of Biomass Micron Fuel (BMF) in a Cyclone Gasifier,” Bioresource Technology, Vol. 100, No. 2, 2009, pp. 1003-1006. doi:10.1016/j.biortech.2008.07.007
- L. Gerun, M. Paraschiv, R. Vijeu, J. Bellettre, M. Tazerout, B. Gøbel and U. Henriksen, “Numerical Investigation of the Partial Oxidation in a Two-Stage Downdraft Gasifier,” Fuel, Vol. 87, No. 7, 2008, pp. 1383-1393. doi:10.1016/j.fuel.2007.07.009
- D. Shin and S. Choi, “The Combustion of Simulated Waste Particles in a Fixed Bed,” Combustion and Flame, Vol. 121, No. 1, 2000, pp. 167-180. doi:10.1016/S0010-2180(99)00124-8
- W. P. Jones and R. P. Lindstedt, “Global Reaction Shcemes for Hydrocarbon Combustion,” Combustion and Flame, Vol. 73, No. 3, 1988, pp. 233-249. doi:10.1016/0010-2180(88)90021-1
- K. M. Bryden and K. W. Ragland, “Numerical Modeling of a Deep, Fixed Bed Combustor,” Energy & Fuels, Vol. 10, No. 2, 1996, pp. 269-275.
- C. K. Westbrook and F. L. Dryer, “Chemical Kinetic Modeling of Hydrocarbon Combustion,” Progress in Energy and Combustion Science, Vol. 10, No. 1, 1984, pp. 1-57. doi:10.1016/0360-1285(84)90118-7
- C. D. Blasi, “Dynamic Behaviour of Stratified Downdraft Gasifiers,” Chemical Engineering Science, Vol. 55, No. 15, 2000, pp. 2931-2944. doi:10.1016/S0009-2509(99)00562-X
- J. Macak and J. Malecha, “Mathematical Model for the Gasification of Coal under Pressure,” Industrial & Engineering Chemistry Process Design and Development, Vol. 17, No. 1, 1978, pp. 92-98.
- A. Jess, “Reaktionskinetische Untersuchungen zur thermischen Zersetzung von Modellkohlenwasserstoffen,” Erdol Erdgas Kohle, Vol. 111, 1995, pp. 479-484.
- P. Morf, P. Hasler and T. Nussbaumer, “Mechanisms and Kinetics of Homogeneous Secondary Reactions of Tar from Continuous Pyrolysis of Wood Chips,” Fuel, Vol. 81, No. 7, 2002, pp. 843-853. doi:10.1016/S0016-2361(01)00216-2
- J. Andreas, “Mechanisms and Kinetics of Thermal Reactions of Aromatic Hydrocarbons from Pyrolysis of Solid Fuels,” Fuel, Vol. 75, No. 12, 1996, pp. 1441-1448. doi:10.1016/0016-2361(96)00136-6
- X. Li, J. Xu, F. Wang, J. Gao, L. Zhou and G. Yang, “Direct Oxidation of Toluene to Benzoic Acid with Molecular Oxygen over Manganese Oxides,” Catalysis Letters, Vol. 108, No. 3, 2006, pp. 137-140. doi:10.1007/s10562-006-0034-x
- Y. Su, Y. Luo, Y. Chen, W. Wu and Y. Zhang, “Experimental and Numerical Investigation of Tar Destruction under Partial Oxidation Environment,” Fuel Processing Technology, Vol. 92, No. 8, 2011, pp. 1513-1524.
Nomenclature
CP Heat capacity at constant pressure (J/kg ˚C)
D Mass diffusion coefficient (m2/s)
E Standard enthalpy (J/kg)
I Radiation intensity k Thermal conductivity kc Arrhenius kinetic rate (k mol/m3s)
A0 Frequency factor p Pressure (Pa)
Pr Prandtl number R gas constant s Special entropy(J/kg mol˚C)
T Temperature u Velocity magnitude (m/s)
v Velocity vector Y Mass fraction
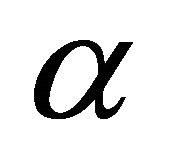 Thermal diffusivity (m2/s)
Thermal diffusivity (m2/s)
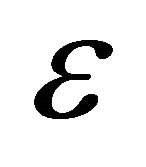 Turbulent dissipation rate (m2/s3)
Turbulent dissipation rate (m2/s3)
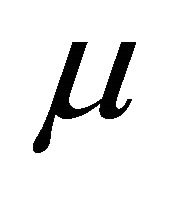 Dynamic viscosity (Pa S)
Dynamic viscosity (Pa S)
 Kinematic viscosity (m2/s)
Kinematic viscosity (m2/s)
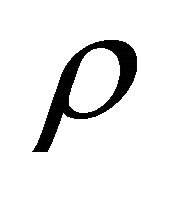 Density (kg/m3)
Density (kg/m3)
Subscripts
i Species i
NOTES
*Corresponding author.

