Energy and Power Engineering
Vol. 4 No. 4 (2012) , Article ID: 20798 , 10 pages DOI:10.4236/epe.2012.44036
CH4/NOx Reduced Mechanisms Used for Modeling Premixed Combustion
1Department of Physics, Faculty of Sciences, Moulay Ismaïl University, Meknès, Morocco
2Laboratory of Heat Transfer and Mass, FST of Mohammadia, Hassan II University, Mohammadia, Morocco
Email: abdobel@yahoo.fr
Received April 20, 2012; revised May 29, 2012; accepted June 10, 2012
Keywords: CSP Method; S-STEP Algorithm; Reduced Mechanism; Methane and Premixed Laminar Flame
ABSTRACT
This study has identify useful reduced mechanisms that can be used in computational fluid dynamics (CFD) simulation of the flow field, combustion and emissions of gas turbine engine combustors. Reduced mechanisms lessen computational cost and possess the ability to accurately predict the overall flame structure, including gas temperature and species as CH4, CO and NOx. The S-STEP algorithm which based on computational singular perturbation method (CSP) is performed for reduced the detailed mechanism GRI-3.0. This algorithm required as input: the detailed mechanism, a numerical solution of the problem and the desired number of steps in the reduced mechanism. In this work, we present a 10-Step reduced mechanism obtained through S-STEP algorithm. The rate of each reaction in the reduced mechanism depends on all species, steady-state and non-steady state. The former are calculated from the solution of a system of steady-state algebraic relations with the point relaxation algorithm. Based on premixed code calculations, The numeric results which were obtained for 1 atm £ Pressure £ 30 atm and 1.4 £ f £ 0.6 on the basis of the ten steps global mechanism, were compared with those computed on the basis of the detailed mechanism GRI-3.0. The 10-step reduced mechanism predicts with accuracy the similar results obtained by the full GRI-3.0 mechanism for both NOx and CH4 chemistry.
1. Introduction
The simulation of combustion in internal combustion engines is important in order to make computer-aided design possible, and also to be able to predict pollutant formation and gain a better understanding of the coupling between the various physical and chemical processes. Accurate simulations of Diesel engines require models for the various processes, such as spray dynamics, ignition, chemistry, heat transfer, etc. as well as the interactions between them, such as chemistry-turbulence interactions, etc. This simulation by using detailed mechanism required very long CPU times and reaching the limits of available memory [1]. Thus, the usefulness of reduced mechanisms ranges from decreasing the computational time all the way to making the simulations feasible. These reduced mechanisms consist of a few steps, which involves only a small number of chemical species and the corresponding rates are linear relations among the elementary rates.
Techniques are now available to create simplified chemical schemes that faithfully represent detailed chemical descriptions over as appropriate range of conditions using many fewer species or progress variables. Among them are: computational singular perturbation (CSP) [2,3], intrinsic low-dimensional manifold methods (ILDM) [4,5], rate-controlled constrained equilibrium (RCCE) [6], repro modeling [7], flame generated manifolds methods (FGM) [8], and Roussel & Fraser algorithm (RF) [9]. While each of these approaches can claim some success, and several have been extensively applied, none of these have achieved the level of applicability and universality of reduced mechanism methods based on steady-state assumption for a number of the chemical species (QSSA) [10,11].
Given a detailed mechanism, the construction of a reduced mechanism requires 1) the identification of the steady state species and the linearly independent elementary reactions that consume the fastest of these species and 2) simple linear algebra calculations. In the past, constructing a validated reduced mechanism was a tedious and time consuming process, made a little easier with the appearance of computer codes being able to handle the linear algebra calculations. These difficulties were surpassed with the development of the algorithmic procedure implemented in the S-STEP algorithm, which is based on CSP and produces reduced mechanisms of arbitrary size [12,13]. The algorithm is fully automatic, identifies the steady state species and fast elementary reactions, requiring as input simply the detailed kinetic mechanism, a reference numerical solution of the flame and the desired number of global steps in the reduced mechanism.
In this work, we reduced the detailed mechanism of the methane combustion in air (GRI-3.0) [14] by using the CSP method. The methodology shall then be applied to methane-air laminar premixed flame for the construction of a ten-step global mechanism. The range of validity of this mechanism will be examined by comparing numerical results thus obtained with those calculated on the basis of the detailed mechanism GRI-3.0 for a wide range of operating conditions.
2. Objectives and Approach
The GRI-3.0 mechanism [14] developed by the Gas Research Institute is considered one of the best mechanisms that accurately describes CH4/NOx chemistry for natural gas combustion. This mechanism involves 325 reactions, 53 species and 5 elements (i.e. K = 325, N = 53, E = 5), included C2 species, prompt and thermal NO, and nitrous oxide chemistry.
The objective of this work was to find a reduced mechanism based on the GRI-3.0 that would describe premixed CH4/air Combustion systems. The full GRI-3.0 mechanism was reduced using a S-STEP algorithm that first identified steady-state species and the fast elementary reactions, requiring as input simply the detailed kinetic mechanism, a reference numerical solution of the flame and the desired number of global steps in the reduced mechanism. This resulted in ten-step reduced mechanism of CH4 combustion coupled with NOx chemistry. The GRI-3.0 mechanism was then used as a benchmark to test the global mechanism using a premixed code. Predictions of this global mechanism were also compared with prediction of CH4 chemistry obtained using the seven-step reduced mechanism [15].
S-STEP code is as interactive program that runs in conjunction with CHEMKIN-II [16] and flame code such as the premixed code. The PREMIX code [17] is more commonly used due to its simplicity, and also because it provides solutions to flame problems more quickly. Figure 1 shows the schematic diagram that explains the interaction between the S-STEP code, CHEMKIN, and a flame code such as the PREMIX code.
As shown in Figure 1, the detailed GRI-3.0 mechanism 1) is first provided to the CHEMKIN interpreter. This produces a linking file 2) that is utilized by the PREMIX code 3) to solve the required problem. The solution from the PREMIX code is stored in a save file 4) which is read by the S-STEP program 5). The save file contains important information related to species concentrations, sensitivity coefficients, and other variables.
3. Construction of 10-Step Reduced Mechanism by Using S-STEP Algorithm
After having a numerical solution obtained by the code PREMIX code for a definite richness, the S-STEP code produces a reduced mechanism with ten global reactions (S = 10) as shown by the following steps.
3.1. Steady State Species Identification
Given the desired number of global steps (S = 10), M = N-S-E = 38 steady-state species must be identified, where N = 53 is the total number of species in the detailed mechanism and E = 5 is the number of elements. For this reason, CSP analysis is performed at each grid point providing the CSP pointer Pi(x) of each species i, which is a function of space and takes a value between zero and unity. After computing, at each grid point, the CSP basis vectors Ar and Br (Ar = [A1, A2, ∙∙∙, AM], Br = [B1, B2, ∙∙∙, BM]T), AS and BS (Ar = [AM+1, ∙∙∙, AN], Br = [BM+1, ∙∙∙, BN]T), which describe the fast and slow subspace, the N diagonal elements Pi of the CSP-pointer:
 (1)
(1)
are recorded, where P is N-dimensional vector. Pi are its elements, the superscript refers to the ith species in the detailed mechanism and their sum equals M. In physical terms, the CSP pointer is measured of the influence of M fastest chemical time scales on each of the species. When
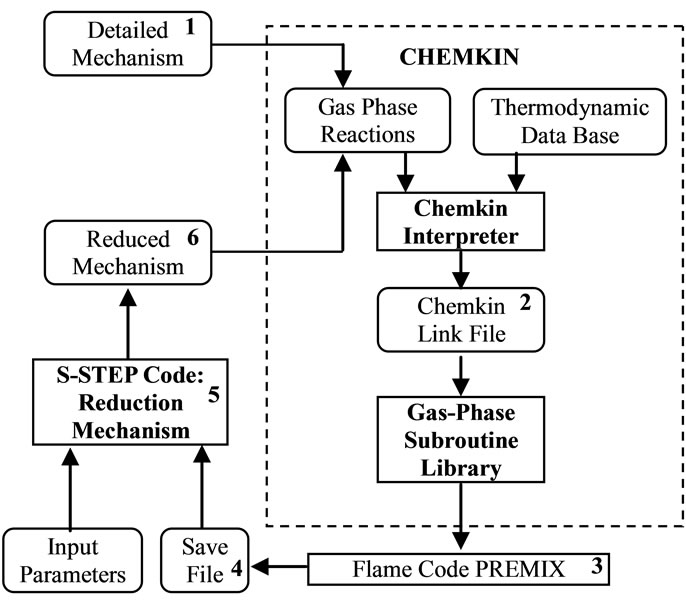
Figure 1. Flow diagram illustrating the relations ship between the S-STEP code, the flame code and CHEMKIN preprocessor package.
Pi(x) = 1.0, the ith species are completely influenced by the fastest scales and are the best candidates to be steady state. In contrast, when Pi(x) = 0.0, the fast time scales have no effect on the ith species and cannot be identified as steady state.
From the results discussed in [12], the CSP-pointer should not be considered alone when selecting the steady state species but the integration of CSP-pointer is used for identify the global steady-state species. The integrated CSP-pointer for each species is defined by the following expression:
 (2)
(2)
where 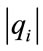 is the net species production rate,
is the net species production rate, 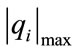 is the corresponding maximum inside the calculation domain of length L and Xi is the species mole fraction. In contrast to the CSP pointers, the scalars Ii can take any value between zero and infinity. The quantities Ii for each species are ordered (see Table 1) and the N − M = 15 species with the lowest values are taken as major (nonsteady-state) species. The M = 38 species with the largest values are identified as steady-state species.
is the corresponding maximum inside the calculation domain of length L and Xi is the species mole fraction. In contrast to the CSP pointers, the scalars Ii can take any value between zero and infinity. The quantities Ii for each species are ordered (see Table 1) and the N − M = 15 species with the lowest values are taken as major (nonsteady-state) species. The M = 38 species with the largest values are identified as steady-state species.
According to this table, the 15-species (CH4, CH3, C2H2, CO, CO2, H2O, H2, O2, OH, H, N2O, HCN, NO, N2 and AR) that produce the smallest value are considered as major species. The remaining species are the steadystate species.
3.2. Fast Reactions Identification
Having selected the M = 38 steady-state species on the basis of the integrate pointer Ii, the corresponding fast elementary reactions are identified as follows. The rate of each elementary reaction is integrated along the flame [12]:
 (3)
(3)
where the subscript k denotes the elementary reactions consuming the ith species. The reactions that consume the steady-state species and exhibit the largest integrated rate are selected and deemed the fast reactions (the rest are slow). For M = 38 steady-state species, M = 38 fast reactions selected.
3.3. 10-Step Reduced Mechanism of Methane
In this section we present and discuss the reduced mechanism constructed for methane flame. We discuss aspects of the reduction procedure by examining the methane mechanisms. The ten-step methane mechanism developed here is compared here with the seven-step methane mechanism taken from [15].
The 10-step mechanism was constructed on the basis of the ordering of Table 1, for f = 1.2, chosen so that a C2 species appears in the major species set which is anticipated to improved predictions for rich flames. The resulting mechanism still consists of 7 steps and 12 species (excluding Ar and considering N2 as an inert), and is given by:
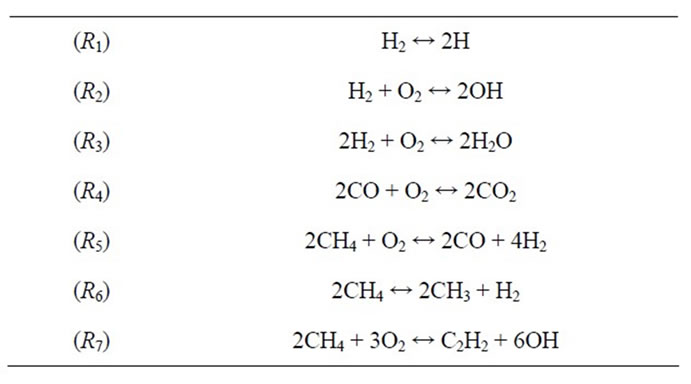
The reactions R1 and R2 describe respectively the formation of the hydrogen (H) and the oxyhydrogen (OH), while reactions R3 and R4 describe the hydrogen to water and carbon monoxide conversions. Reactions R5 and R6 represent the conversion of CH4 → CH3 → H2 and CO, R7 account for the formation of C2 species, such as C2H2.
We further note in the present study that the species O is identified as steady-state species. In fact, extensive validation [18-20] appears to support the validity of this assumption in methane oxidation over a wide range of combustion phenomena and under extensive thermodynamical parametric variations.
With the additional consideration of NO, N2O and HCN, S-STEP yielded a 10-step mechanism by including the following tree global reactions:
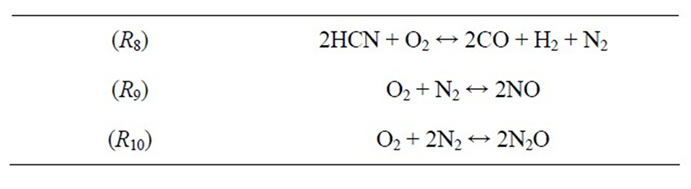
Note that R8 involves the prompt and reburning reactions. Moreover, R9 describes the thermal NO pathway, which is the dominant NO formation path due to the high temperatures involved. R10 describes the formation of the nitrous oxide pathway.
A comparison between seven-step mechanism, the 10-step mechanism contains the additional species C2H2, CH3 and HCN. Those species should appear in a reduced mechanism valid for rich flames. Finally, note that N2O appears in both mechanisms as major species, in contrast to other reduced mechanisms.
From this mechanism, it is shown that the 7-step reduced mechanism [15] is a subset of the 10-step one. The reactions R1-R5 and R9-R10 of the 10-step one contain the seven-step mechanism [15]. The first six global reactions
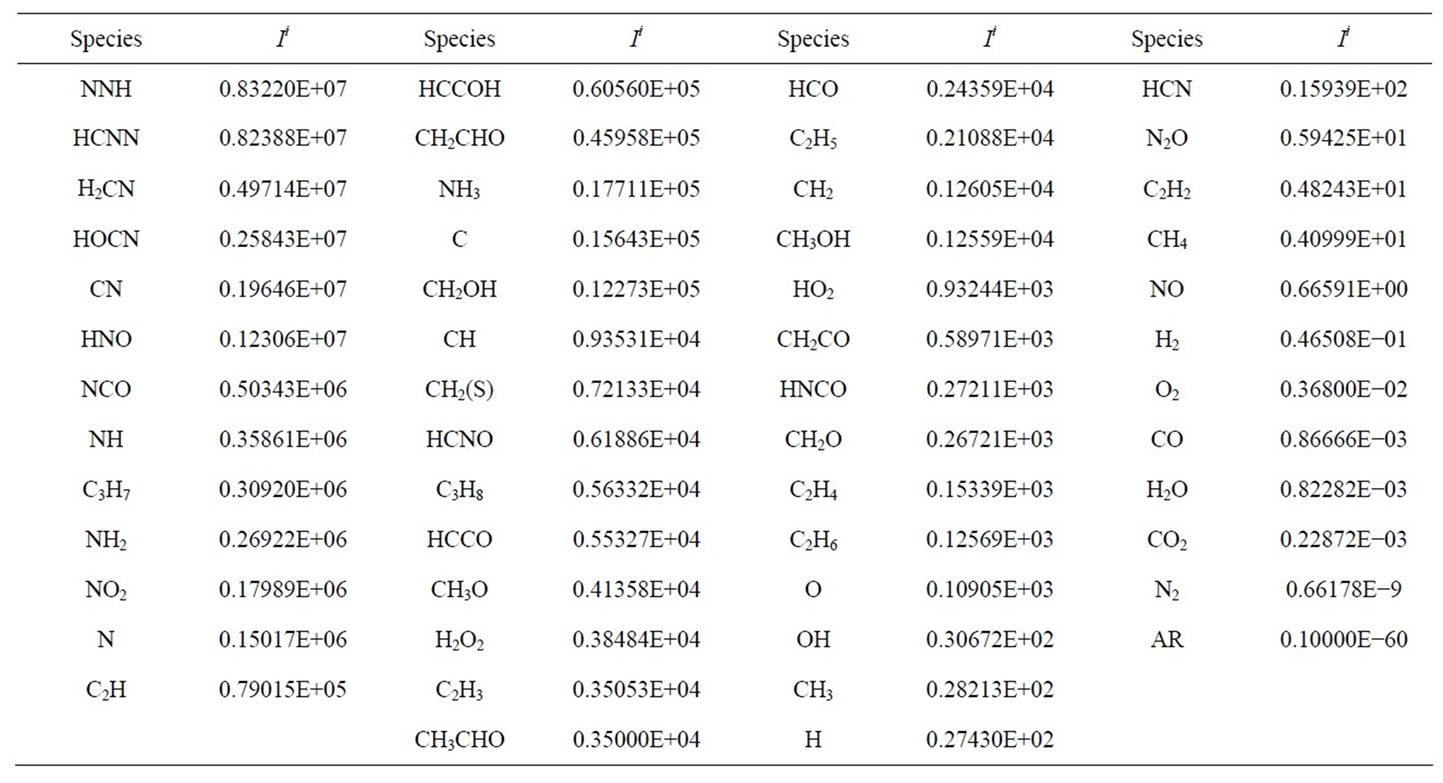
Table 1. Integrate CSP-pointer.
in the 10-step mechanism describe methane combustion and the rest nitrogen chemistry.
The global rates Rwj (j = 1 to 10) of this mechanism are a linear combination of elementary rates wi (i = 1 to 325) in the detailed mechanism GRI-3.0 and are listed in Appendix A. These rates depend, of course, on all species, steady state and non-steady state. The former are calculated from the solution of a system of steady-state algebraic relations with the inner iteration procedure.
4. Results and Discussion
The numerical which were obtained for 1 atm £ Pressure £ 40 atm and 0.6 £ f £ 1.4 on the basis of the ten steps global mechanism, were compared with those computed on the basis of the detailed mechanism GRI-3.0 and 7-step reduced mechanism.
Using the reduced mechanism (R1-R10) it was shown that numerical solutions were obtained about 3.5 times faster than when using the detailed mechanism. This decease of CPU time is in agreement with the reasoning of Somers and Go Goey [21].
4.1. Flame Propagating Velocity
An important characteristic of laminar premixed flames, often used as a global performance test for reduced mechanisms, is the flame propagation velocity, Sl. With the 10-step reduced mechanism developed here, the calculation of planar flames results in errors in Sl typically smaller than 15% for varying conditions of mixture composition and pressure. This is illustrated in Figures 2 and 3, where the of Sl obtained with the reduced mechanisms (10-step and 7-step is compared with that obtained with detailed chemistry (GRI-3.0).
Figure 3 shown the comparison of flame propagation velocity Sl = ru/ru (r is the mixture density, u is the gas velocity and ru is unburned gas density), as a function of mixture pressure for CH4-air flames for different mixtures (f = 0.6, 1.0 and 1.4). Observation of this figure indicates that the reduced mechanisms produce the accurate values for this intrinsic parameter in particular for the lean and rich mixtures. A similar agreement is found for the dependence of the flame propagation velocity on the mixture composition. This is investigated in Figure 4, where we plot the variation of Sl with equivalence ratio (f).
4.2. Structure Flame
The characteristic flame structure corresponding to the reduced mechanism is shown in Figures 4 and 5, along with the results of the detailed chemistry and 7-step reduced mechanism. In Figure 4, calculated mole fraction profiles for CH4, CO2, CO, O2, H2, H2O, O, H and OH are compared with those computed using GRI-3.0 and 7-step reduced mechanism.
From those Figures 4(a)-(c), it is seen that the two reduced mechanisms (10-step and 7-step) show a excellent prediction of the carbon monoxide profile along the flame. The agreement for all other major species is at least as good as for the monoxide, to the point that most
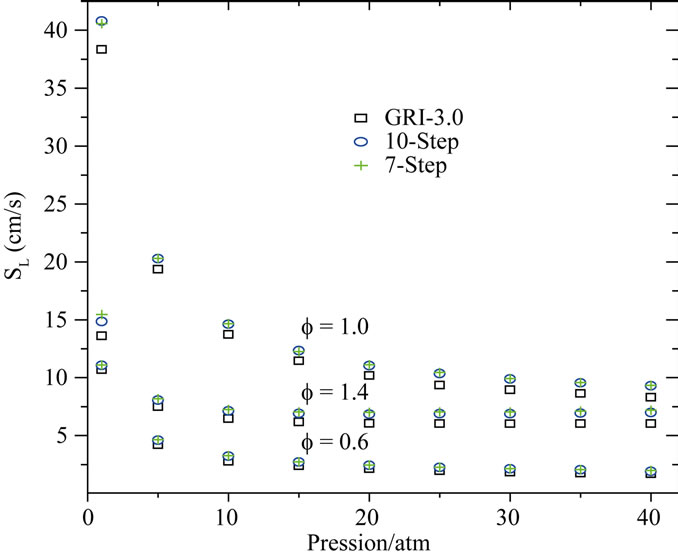
Figure 2. The flame propagation velocity as a function of the pressure for different equivalence ratios (f = 0.6, 1.0 and 1.4) and Tu = 300 K.

Figure 3. The flame propagation velocity as a function of the equivalence ratio for P = 1 bar and Tu = 300 K.
curves are indistinguishable on the graphs. The Figure 4(c) shown that the developed reduced mechanism have a better prediction of the species CO, H, OH, O2 and CH4 in comparison with 7-step reduced mechanism.
The following Figure 5 shows the predictions of the final temperature at the point x = 3.0 cm as a function of the equivalence ratio (f).
In Figure 6, we present the final mole fraction of NO according to the richness at the point x = 3.0.
It is shown from this figure that the NO at the end of the computational domain is produced correctly by the seven-step mechanism for equivalence ratio lower than 1 (lean mixtures), while the 10-step mechanism gives excellent prediction even for very rich flame. The peak NO occurs at stoichiometry and the error between the reduced and detailed mechanisms is around 6.5%, which is
 (a)
(a)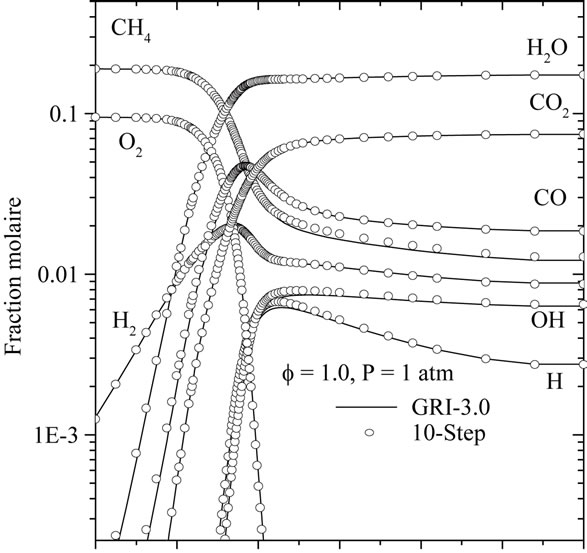 (b)
(b)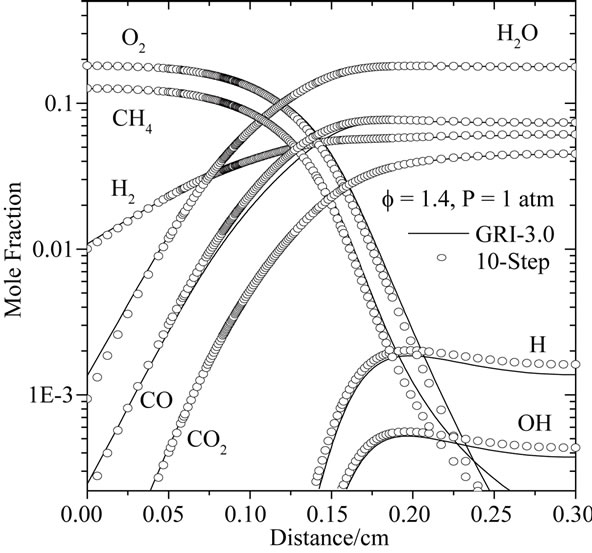 (c)
(c)
Figure 4. Comparison of predicted profiles of CH4, CO2, CO, O2, H2, H2O, O, H and OH for atmospheric, freelypropagating, CH4-air mixtures with Tu = 300 K: (a) f = 0.6; (b) f = 1.0; and (c) f = 1.4.
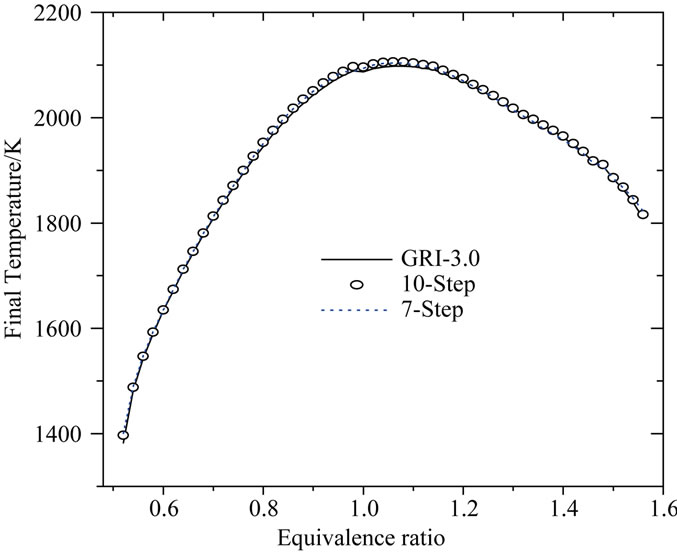
Figure 5. Final temperature at the point x = 3.0 as a function of equivalence ratio.
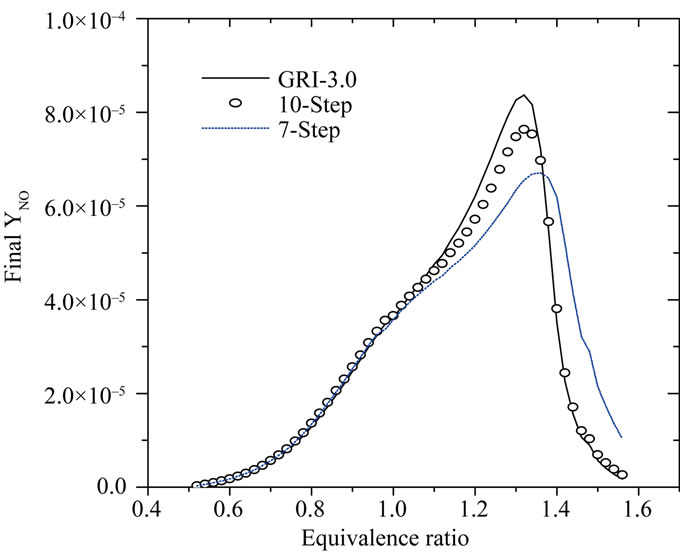
Figure 6. NO mole fraction at x = 3.0 cm as a function of the equivalence ratio for methane premixed flames.
considered small.
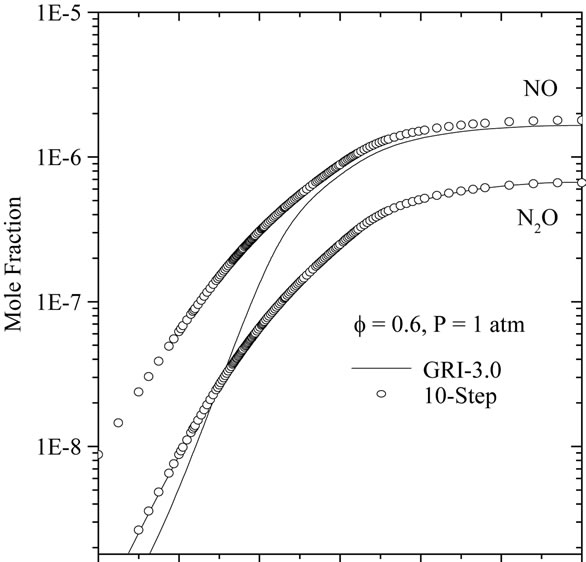
Figures 7(a)-(c) compares the spatially resolved species profiles of NO and N2O for atmospheric, freely propagating methane/air flames at equivalence ratios (f) of 0.6, 1.0, and 1.4, respectively.
According to Figures 7(a) and (b), we can note the existence of an initial region of rapid NO growth associated with equilibrium radical concentrations, followed by a region of slow growth (small slope). The reduced mechanisms over predicts the nitric oxide in the reaction zone. This difference between the two results becomes clearly distinguished in the case of a lean flame (see Figure 4(a)). In Figure 4(c), it is shown clearly that the developed mechanism (10-step) better predict the mole fraction relating to the species NO and N2O in comparison with 7-step reduced mechanism. This is due to the presence of C2-chemistry in 10-step reduced mechanism.
 (a)
(a) (b)
(b)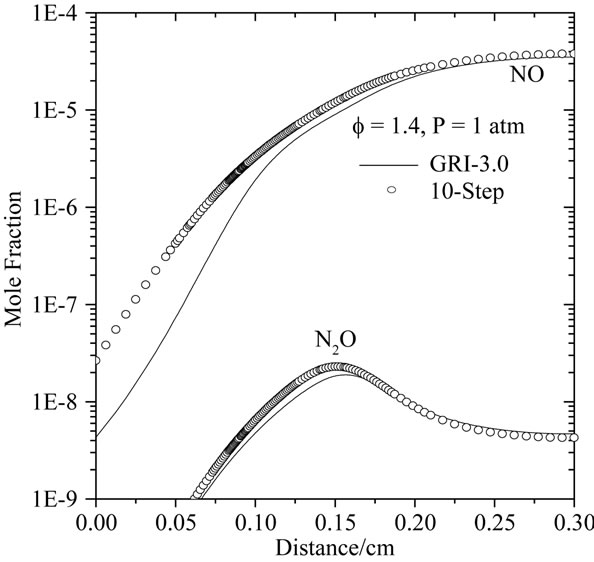 (c)
(c)
Figure 7. Comparison of predicted profiles of NO and N2O for atmospheric, freely-propagating, CH4-air mixtures with Tu = 300 K: (a) f = 0.6; (b) f = 1.0; and (c) f = 1.4.
For P = 30 atm: Figures 8 and 9 show the numerical calculation of the major species and radical concentrations profiles of the stoiciometric mixture of methane/air.
As in the case of atmospheric pressure (P = 1 atm), predictions of the mole fractions of CH4, CO2, CO, O2, H2, H2O, O, H and OH are presented on the Figure 8 for f = 1. Consequently, the combustion rates predicted by the two reduced mechanisms with ten and seven steps are similar to detailed mechanism GRI-3.0 for a pressure of 30 atm. The peak CO concentrations are reproduced accurately by two reduced mechanism. The CO2 formation rate is similar for the reduced and full mechanisms at all conditions shown, included the effect of pressure.
Figure 9 shows predicted NO and N2O mole fractions as a function of distance along the premixed flame. The NO formation is largely dependent on the other conditions within the reactor (i.e. temperature, major and minor species concentrations). Figure 9 shows that at 30 atm and f = 1.0, the peak NO mole fraction is predicted reasonably well by the ten-step and seven-step reduced mechanisms.
It is obvious from the presented figures that the agreement between the two reduced mechanisms (ten-step and seven-step) and the detailed mechanism is reasonable. This shows that the principal characteristics of the flame are described reasonably by the two reduced mechanisms for different richness and pressures. In fact, it is seen that the two reduced mechanisms produce correct evolutions of the important parameters such as the flame propagation velocity the temperature and the mole fractions of the major species.
5. Conclusion
A major subject or this work was to develop mechanism
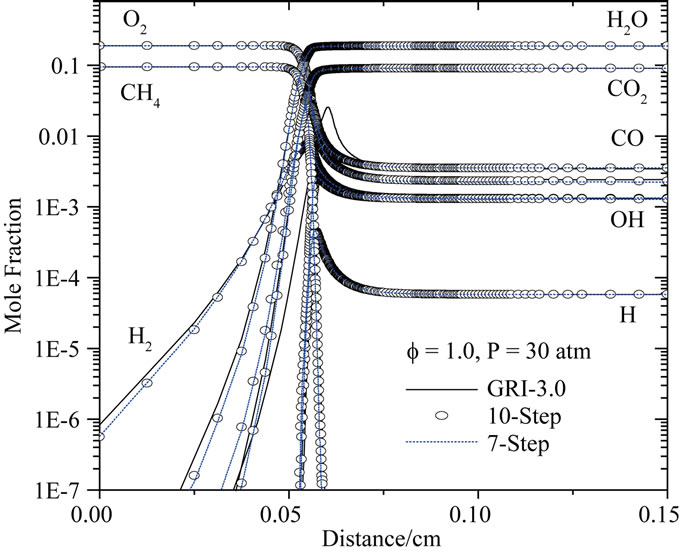
Figure 8. Comparison of predicted profiles of CH4, CO2, CO, O2, H2, H2O, O, H and OH for P = 30 atm, Tu = 300 K and f = 1.0.

Figure 9. Comparison of predicted profiles of NO and N2O for P = 30 atm, Tu = 300 K and f = 1.0.
of CH4 combustion and NOx formation that describe premixed combustion of methane.
A reduced mechanism for methane-air combustion with NO formation has been constructed with the computational singular perturbation method using a S-STEP automatic algorithm. The analysis was made on solution of adiabatic premixed flame with detailed kinetics described by GRI-3.0 for methane that includes NOx formation. A ten-step methane mechanism has been constructed which reproduces accurately flame speeds, flame temperatures and mole fraction distributions of major species for whole flammability range. Many steady-state species are also predicted satisfactory. It uses CH4, O2, H2O, CO2, CO, H2, OH, H, NO, N2O, HCN, CH3 and C2H2 as major species and it has been derived from a CP analysis at f = 1.2. Comparison with our previous sevenstep mechanism, which was derived at f = 1.0, shows that the improved accuracy in the calculation of C2-species and HCN results in much better predictions for prompt NO, especially for very rich mixtures. This mechanism performs well for the whole flammable range of equivalence ration and for pressures up to 30 atm.
REFERENCES
- E. F. Christos and B. Konstantinos, “Analysis and Reduction of the CH4-Air Mechanism at Lean Conditions,” Combustion Science and Technology, Vol. 159, 2000, pp. 281-303. doi:10.1080/00102200008935787
- S. H. Lam and D. A. Goussis, “Understanding Complex Chemical Kinetics with Computational Singular Perturbation,” 22nd Symposium on Combustion, The Combustion Institute, Pittsburgh, 1988, p. 931.
- S. H. Lam and D. A. Goussis, “Reduced Kinetic Mechanisms and Asymptotic Approximations for Methane-Air flames,” In: M. Smooke, Ed., Springer Lecture Notes 384, 1991, p. 227.
- U. Maas and S. B. Pope, “Implementation of Simplified Chemical Kinetics Based on Intrinsic Low-Dimensional Manifolds,” 24th Symposium (International) on Combustion, The Combustion Institute, Pittsburgh, 1992, pp. 103-112.
- U. Maas and S. B. Pope, “Simplifying Chemical Kinetics: Intrinsic Low-Dimensional Manifolds in Composition Space,” Combustion and Flame, Vol. 88, No. 3-4, 1992, pp. 239-264. doi:10.1016/0010-2180(92)90034-M
- J. C. Keck, “Rate-Controlled Constrained Equilibrium Theory of Chemical Reactions in Complex Systems,” Progress in Energy and Combustion Science, Vol. 16, No. 2, 1990, pp. 125-154. doi:10.1016/0360-1285(90)90046-6
- T. Turanyi, “Parameterization of Reaction Mechanisms Using Orthogonal Polynomials,” Computational Chemistry, Vol. 18, 1994, pp. 45-54. doi:10.1016/0097-8485(94)80022-7
- J. A. Van Oijen and L. P. H. de Geoy, “Modelling of Premixed Laminar Flames Using Flamelet-Generated Manifolds,” Combustion Science and Technology, Vol. 161, 2000, pp. 113-137. doi:10.1080/00102200008935814
- M. R. Roussel and S. J. Fraser, “Geometry of the Steady- State Approximation, Perturbation and Accelerated Convergence Methods,” Journal of Physics Chemistry, Vol. 97, 1993, pp. 8316-8327. doi:10.1021/j100133a031
- M. D. Smooke, Eds., “Reduced Kinetic Mechanisms and Asymptotic Approximations for Methane-Air Flames,” Springer-Verlag, Berlin, 1991.
- N. Peters and B. Rogg, Eds., “Reduced Kinetic Mechanisms for Application in Combustion Systems,” SpringerVerlag, Berlin, 1993.
- A. Massias, D. Diamantis, E. Mastorakos and D. A. Goussis, “An Algorithm for the Construction of Global Reduced Mechanisms with CSP Data,” Combustion and Flame, Vol. 117, 1999, pp. 117-685. doi:10.1016/S0010-2180(98)00132-1
- G. Skevis, D. A. Goussis and E. Mastorakos, “Understanding Flame Kinetics from CSP Generated Reduced Mechanisms,” European Combustion Meeting, Paper 008, Orleans, 2003.
- C. Bowman, R. Hanson, D. Davidson, W. J. Gardiner, V. Lissianski, G. Smith, D. Golden, M. Frenklach and M. Goldenberrg, “GRI-3.0 Detailed Mechanism,” Berkeley, 2004. http//www.me.berkeley.edu/gri\_mech/
- A. Belcadi, E. Chatri, E. Affad and M. Assou, “7-Step Reduced Mechanism of the Detailed Mechanism GRI-3.0 by Using the CSP Method,” Physical and Chemical News, Vol. 31, 2006, pp. 61-69.
- R. J. Kee, J. F. Grcar, M. D. Smooke and J. A. Miller, “A Fortran Program for Modelling Steady Laminar OneDimensional Premixed Flame,” Report, SAND85-8240. UC-401, Sandia Natinal Laboratories, New Mexico, 1992.
- R. J. Kee, F. M. Rupley and J. A. Miller, “CHEMKIN II: A Fortran Chemical Kinetics Package for the Analysis of Gas-Phase Chemical Kinetics,” Report, SAND85-8240. UC-706, Sandia Natinal Laboratories, New Mexico, 1992.
- C. J. Sung, C. K. Law and J.-Y. Chen, “An Augmented Reduced Mechanism for Methane Oxidation with Comprehensive Global Parametric Validation,” Proceedings of the Combustion Institute, Vol. 27, 1998, pp. 295-304.
- C. J. Sung, C. K. Law and J.-Y. Chen, “Further Validation of an Augmented Reduced Mechanism for Methane Oxidation: Comparison of Global Parameters and Detailed Structure,” Combustion Science and Technology, Vol. 156, 2000, pp. 201-220. doi:10.1080/00102200008947303
- C. J. Sung, C. K. Law and J.-Y. Chen, “Augmented Reduced Mechanism for NO Emission in Methane Oxidation,” Combustion and Flame, Vol. 125, 2001, pp. 906- 919. doi:10.1016/S0010-2180(00)00248-0
- L. M. T. Somers and L. P. H. De Goey, “Analysis of a Systematical Reduction Technique,” 25th Symposium on Combustion, The Combustion Institute, Pittsburgh, 1994, p. 975. doi:10.1115/1.2818457
Appendix A: The Global Rates
Rw1 = −2w1 − 2w2 − 2w4 − w5 − w6 + w7 − w8 + w9 − w11 − w12 − 2w13 − w14 − 2w16 − 2w17 − w22 − w23 − 2w24 + 2w25 − 2w27 +2w29 + 2w30 + w31 + 2w32 − 2w39 − 2w40 − 2w41 − 2w42 − w43 − w44 − 2w45 − 2w46 − w47 − 2w48 − w50 − w52 − w53 − 2w54 − 2w55 − 2w59 − 2w60 − 2w61 − 2w62 − 2w63 − 2w65 − 2w66 − 2w67 − w70 − 2w71 − 2w72 − 2w77 − 2w78 − w79 + 2w80 + 2w81 − 2w82 + w84 + w85 + w86 − w87 − w90 + w91 + w92 + w93 + w94 + w99 − w100 + w101 − w102 − w103 + w104 + w105 + w106 − 2w107 + w111 + w112 − w113 + 3w114 − w115 − w116 − w117 − w118 − w120 + w121 − w122 − w123 − w124 + w125 − w129 − 2w130 − w131 − 3w133 − w134 + w135 + w136 − w138 − 3w140 − w141 + w144 + w146 − w149 − w154 + 2w155 − w160 + w161 + w162 + w163 + w164 − w165 + w171 + w172 + 2w173 + 2w174 − w181 − w182 − w183 + w184 + w185 − 2w186 − 2w187 − w190 − w191 − w192 − w194 − w195 − w196 − 2w197 − w198 − w201 + w203 − 2w207 − w208 − 2w209 − w210 − w211 − 2w212 + w215 + 2w216 − w217 − w219 − w222 + w224 − w225 + w227 + 2w230 − 2w238 + w242 + w243 − w245 + w248 + w256 − w257 − 2w258 + w259 + w260 − 2w261 + w262 − w263 + w267 + w268 + 2w269 − w274 + w275 − w276 + w278 − 2w280 + w282 − w283 − w287 − w289 + 2w290 + w291 + 2w292 + 2w295 − 2w296 + 2w298 − 2w299 + w301 + w302 + w303 + 2w305 + 2w306 + 5w307 + 2w308 − 2w309 − w310 + 5w311 − 2w313 − 2w314 − w315 + w316 − w317 + 2w322
Rw2 = + 2w1 + 2w2 + 2w3 + 3w4 + 3w5 − w7 − w9 + 2w11 + w12 + 3w13 + 2w14 + 2w15 + 3w16 + 3w17 + 2w18 + 2w19 + 7w20 + 3w22 + 8w23 + 2w24 + 2w27 + 8w28 − 6w29 + w30 − w31 − w32 − w33 − w34 − w35 − w36 − w37 − w43 + w45 + 3w46 + w47 + 3w48 − w50 + w55 − w56 − w57 + w60 + 3w61 + 3w62 + w65 + 3w66 + 3w67 − w70 + 6w71 − 6w73 + 8w79 − 8w80 − w81 + 6w82 − w83 − w84 − 5w85 − 3w86 − 2w90 − 3w91 − 3w92 − w93 − 3w94 − 3w95 − w98 − w99 − w101 − w104 − w105 − 3w106 + 6w107 + 5w110 − 7w111 − w112 − w113 − 9w114 + w118 + 2w120 − w121 − 2w122 − 7w123 − 7w124 − 3w125 − 2w127 − 8w128 − w129 − w130 − 8w131 − 2w132 + w133 − w136 − 8w137 − w138 − w139 + 6w141 − w145 − w146 − 3w147 − w149 − w150 − 2w153 − w154 − 3w155 + w157 + w160 + w166 + w167 + 5w171 − w172 − 2w173 − 6w174 − w175 + 8w176 + 8w177 − 2w178 − 2w179 − 2w180 + w181 + w182 + w183 − 2w184 − w185 + 3w186 + 2w187 + 2w190 + 2w191 + w193 + 2w195 + w197 + 2w198 + w199 − 2w202 − 3w203 − w206 + 2w207 − w210 + 2w213 − w215 − w216 + 2w217 − 2w218 + w219 − 2w220 + 2w222 + w226 + 2w227 + w228 + w229 + 2w233 − 2w242 − 2w243 − 2w244 − 2w246 − 2w247 − w248 + w256 − 3w259 − 3w260 − w262 − 2w266 − 3w267 − w268 − 2w269 + 8w274 − w275 − w276 − w278 + 2w279 + w280 − 2w281 − w283 + w284 + 2w285 − 2w288 − w289 − w290 − 3w291 − 8w292 − 2w293 − 7w295 + 5w296 + 3w297 + 2w299 + w300 + w303 + w305 − w306 − 2w307 − 2w308 − w310 − 5w311 + 2w313 − w315 + w316 − 3w322 + w323 + w324
Rw3 = − w5 + w6 + w7 + w8 + w9 − w22 − w23 − w30 + w43 + w44 − w47 + w50 + w70 − w79 + w84 + w85 + w86 + w87 + w90 + w91 + w92 + w93 + w94 + w98 + w100 + w101 + w102 + w103 + w104 + w105 + w106 + w111 + w112 + w113 + w114 + w115 + w116 + w117 + w121 + w122 + w123 + w124 + w125 + 2w128 + w129 + w130 + w131 + w132 + w133 + w134 + w135 + w136 + 2w137 + w138 + w139 + w140 + w141 + w0+ 2w145 + w146 + w149 + w150 + w153 + w154 − w157 + w171 + w172 + w178 + w179 + w180 − w191 + w196 − w197 + w200 + w201 + w202 + 2w203 + w210 + w215 − w217 − w219 + w225 − w227 − w235 − w236 + w242 + w243 + w244 + w246 + w247 + w250 + w253 + w255 + w257 + w258 + w259 + w260 + w262 + w263 + w264 + w266 + 2w267 + w269 + w271 − w273 − w274 + w275 + w276 + w278 + w283 + w287 + w289 + w290 + w291 + 2w292 + w301 + w302 − w305 + w310 + w315 − w316
Rw4 = + w12 + w14 + w30 + w31 + w99 + w120 − w132 − w153 + w226 + w229 + w262 + w268 − w280 + w282 − w283 + w290 + w305
Rw5 = + 2w4 + 2w6 + 2w8 − w11 + 2w13 + 2w14 + 2w16 + 2w17 + 2w28 + 2w29 + 2w30 − 2w32 − 2w33 − 2w34 − 2w35 − 2w36 − 2w37 + 2w44 + 2w45 + 2w46 + 2w48 + w52 − w53 + 2w55 − 2w56 − 2w57 + 2w60 + 2w61 + 2w62 + 2w65 + 2w66 + 2w67 − 2w71 + 2w73 + 2w80 + 2w81 − 2w82 − 2w83 − 2w85 + 2w87 + 2w90 − 2w95 − w98 + 2w100 + 2w102 + 2w103 − 2w107 + 2w111 + 2w114 + 2w115 + 2w116 + 2w117 + 3w118 + 2w120 + 2w122 + 2w123 + 2w124 + 2w128 − w130 + 2w134 + 2w135 + 2w137 − w139 − 2w140 + 2w144 + 2w145 − 2w147 − w150 − 2w155 + w157 + 3w160 + w161 + w162 + w163 + w164 + w165 + 2w166 + 2w167 + 2w174 − 2w175 + 2w176 + 2w177 + 2w178 + 2w179 + 2w180 − 2w184 + 2w186 − 2w191 − 2w193 + 2w196 + 2w200 + 2w201 + 2w202 + 2w203 − 2w206 + w211 − 2w216 − 2w217 + 2w225 − 2w227 − 2w235 − 2w236 + 2w242 + 2w243 + 2w244 + 2w246 + 2w247 − 2w248 + 2w250 + 2w253 + 2w255 + 2w256 + 2w257 + 2w258 + 2w262 + 2w263 + 2w264 + 2w266 + 2w267 + 2w269 + 2w271 − 2w273 + 5w275 + 5w276 + 2w283 + 2w284 + 2w287 + 2w290 + 2w292 + 2w297 + 2w300 + 2w301 + 2w302 + 3w303 + 2w305 + 2w306 − 2w311 + w317 − 2w322 + 2w323 + 2w324
Rw6 = − w4 − w6 − w8 + w11 − w13 − w14 − w16 − w17 + w20 + w23 − 2w29 − w30 + w32 + w33 + w34 + w35 + w36 + w37 − w44 − w45 − w46 − w48 − w52 + w53 − w55 + w56 + w57 − w60 − w61 − w62 − w65 − w66 − w67 + 2w71 − 2w73 + w79 − 2w80 − w81 + 2w82 + w83 + w85 − w87 − w90 + w95 + w98 − w100 − w102 − w103 + 2w107 + w110 − 2w111 − 2w114 − w115 − w116 − w117 − 2w118 − w120 − w122 − 2w123 − 2w124 − 2w128 + w130 − w131 − w134 − w135 − 2w137 + w139 + w140 + w141 − w144 − w145 + w147 + w150 + w155 − w157 − 2w160 − w161 − w162 − w163 − w164 − w165 − w166 − w167 + w171 − 2w174 + w175 − w178 − w179 − w180 + w184 − w186 + w191 + w193 − w196 − w200 − w201 − w202 − w203 + w206 − w211 + w216 + w217 − w225 + w227 + w235 + w236 − w242 − w243 − w244 − w246 − w247 + w248 − w250 − w253 − w255 − w256 − w257 − w258 − w262 − w263 − w264 − w266 − w267 − w269 − w271 + w273 + w274 − 2w275 − 2w276 − w283 − w284 − w287 − w290 − 2w292 − w295 − w297 − w300 − w301 − w302 − 2w303 − w305 − w306 + w311 − w317 + w322 − w323 − w324
Rw7 =− w20 − w23 − w28 + w29 − w71 + w73 − w79 + w80 − w82 − w107 − w110 + w111 + w114 + w123 + w124 + w128 + w131 + w137 − w141 − w171 + w17 4 − w176 − w177 − w274 + w292 + w295
Rw8 = − w178 − w179 − w180 + w190 + 2w191 + w192 + 2w193 + w194 + w195 + w197 + w198 + w199 − w200 − w202 − w203 − w208 + 2w217 + w222 + w224 + w226 + 2w227 + w228 + w229 + w235 + w236 − 2w242 − 2w243 − w244 + w245 − w246 − w247 + w248 − w250 − w253 − w255 − w256 − w258 − w262 − w264 − w266 − w267 − w269 − w271 + w273 − 2w275 − 2w276 + w280 + w282 − w283
Rw9 = − w178 + w179 + w180 + 2w182 + w190 + w192 + w194 + w195 + w197 − w198 − w199 − w200 − w202 − w203 + w208 + w222 + w224 + w226 − w228 − w229 + w235 + w236 − w244 − w245 − w246 − w247 − w248 − w250 − w253 − w255 − w256 + w258 − w262 − w264 − w266 − w267 − w269 − w271 + w273 + w280 − w282 + w283
Rw10 = − w181 − w182 − w183 − w184 − w185 + w199 + w228 + w282

