Advances in Pure Mathematics
Vol.3 No.1A(2013), Article ID:27572,8 pages DOI:10.4236/apm.2013.31A032
Oscillation Theorems for a Class of Nonlinear Second Order Differential Equations with Damping
School of Science, Beijing University of Civil Engineering and Architecture, Beijing, China
Email: xjwang@bucea.edu.cn
Received November 8, 2012; revised December 7, 2012; accepted December 14, 2012
Keywords: Nonlinear Differential Equations; Damping Equations; Second Order; Oscillation Solutions
ABSTRACT
The oscillatory behavior of solutions of a class of second order nonlinear differential equations with damping is studied and some new sufficient conditions are obtained by using the refined integral averaging technique. Some well known results in the literature are extended. Moreover, two examples are given to illustrate the theoretical analysis.
1. Introduction
In this paper, we are concerned with the oscillatory behavior of solutions of the second-order nonlinear differential equations with damping
 (1.1)
(1.1)
where 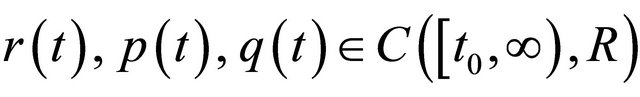 and
and 
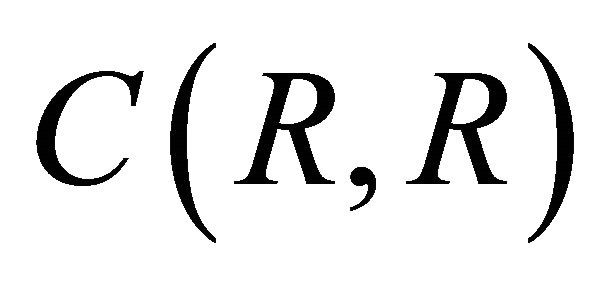 .
.
In what follows with respect to Equation (1.1), we shall assume that there are positive constants 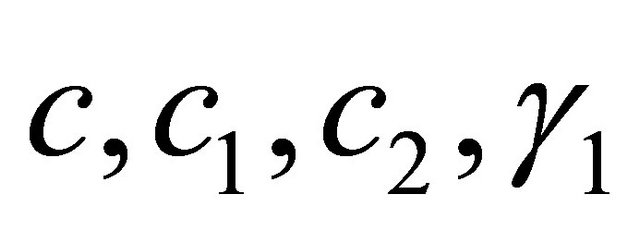 and
and 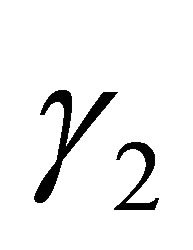 satisfying
satisfying
(A1) 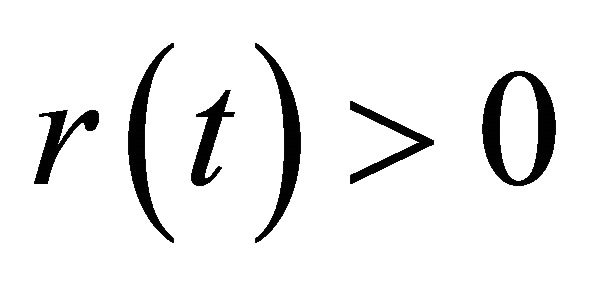 and
and 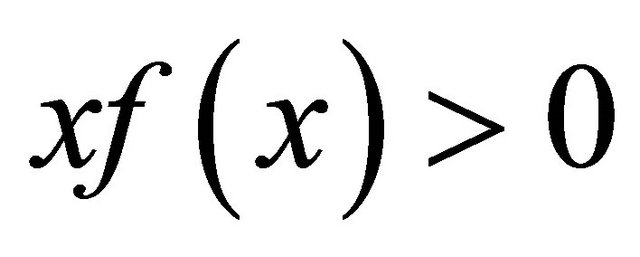 for all
for all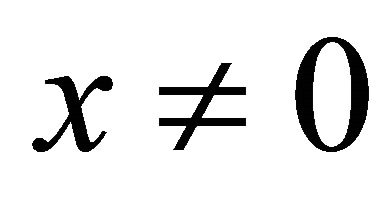 ;
;
(A2)  for all
for all ;
;
(A3) 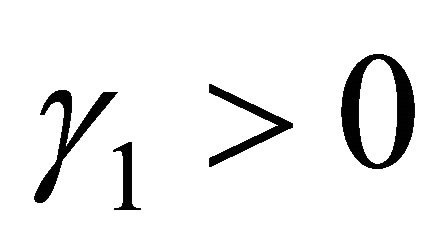 and
and  for all
for all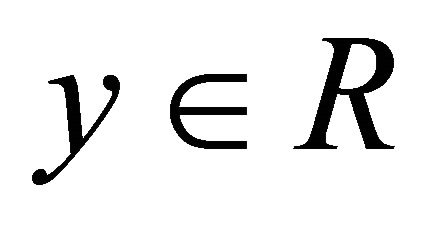 ;
;
(A4)  and
and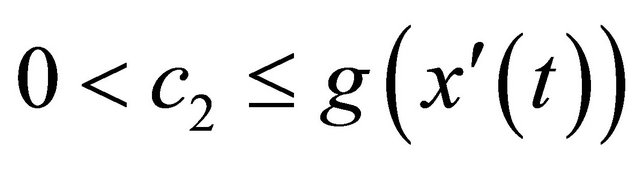 ;
;
(A5)  for all
for all .
.
We shall consider only nontrivial solutions of Equation (1.1) which are defined for all large t. A solution of Equation (1.1) is said to be oscillatory if it has arbitrarily large zeros, otherwise it is said to be nonoscillatory. Equation (1.1) is called oscillatory if all its solutions are oscillatory.
The oscillation problem for various particular cases of Equation (1.1) such as the nonlinear differential equation
 , (1.2)
, (1.2)
the nonlinear damped differential equation
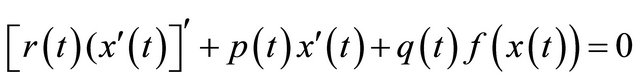 (1.3)
(1.3)
and
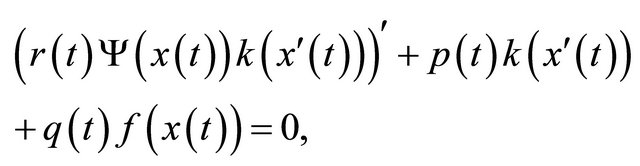 (1.4)
(1.4)
have been studied extensively in recent years, see e.g. [1-21] and the references quoted therein. Moreover, in 2011, Wang [22] established some oscillation criteria for Equation (1.1) firstly, some new sharper results are obtained in the present paper.
An important method in the study of oscillatory behaviour for Equations (1.1)-(1.4) is the averaging technique which comes from the classical results of Wintner [19] and Hartman [18]. Using the generalized Riccati technique and the refined integral averaging technique introduced by Rogovchenko and Tuncay [20,21], several new oscillation criteria for Equation (1.1) are established in Section 2, we also show some examples to explain the application of our oscillation theorems in Section 2. Our results strengthen and improve the recent results of [1] and [21,22].
2. The Main Results
Following Philos [10], let us introduce now the class of functions  which will be extensively used in the sequel. Let
which will be extensively used in the sequel. Let
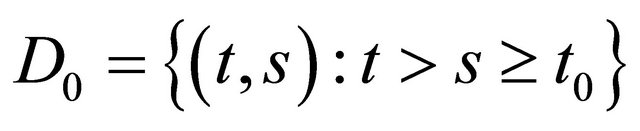 and
and .
.
The function 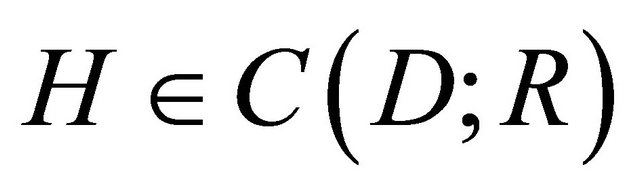 is said to belong to the class
is said to belong to the class  if 1)
if 1) 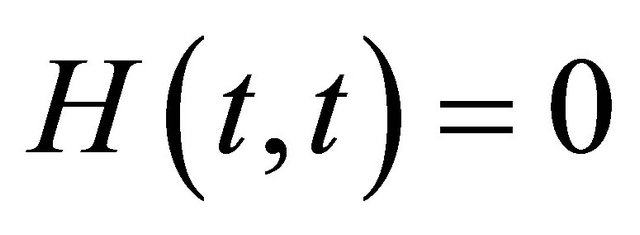 for
for ;
; 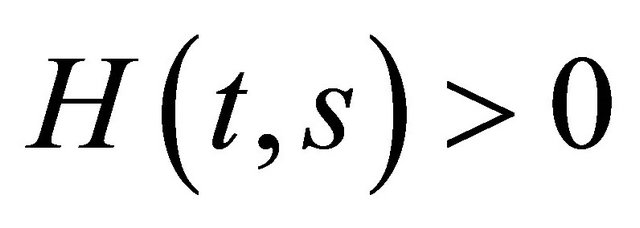 on
on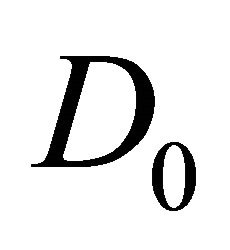 ;
;
2)  has a continuous and nonpositive partial derivative on
has a continuous and nonpositive partial derivative on 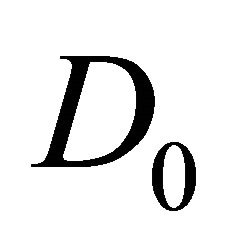 with respect to the second variable;
with respect to the second variable;
3) There exists a function  such that
such that
 .
.
In this section, several oscillation criteria for Equation (1.1) are established under the assumptions (A1)-(A5). The first result is the following theorem.
Theorem 2.1. Let assumption (A1)-(A5) be fulfilled and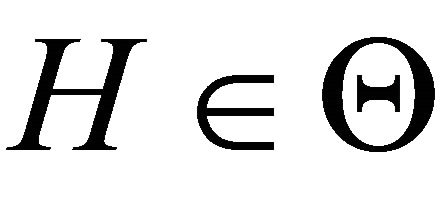 . If there exists functions
. If there exists functions 
such that 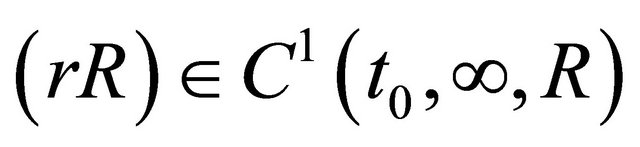 and
and
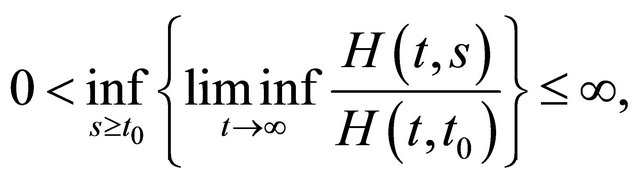 (2.1)
(2.1)
 (2.2)
(2.2)
and for any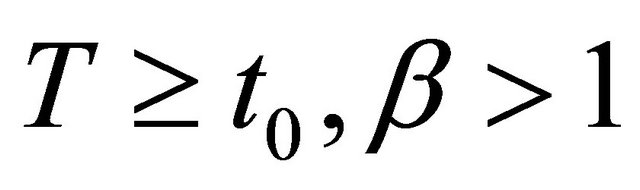 ,
,
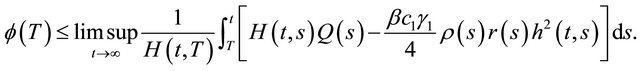 (2.3)
(2.3)
where
 (2.4)
(2.4)
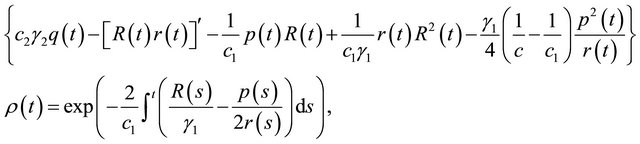 (2.5)
(2.5)
and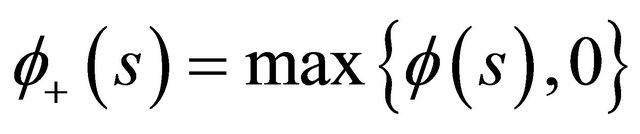 , then Equation (1.1) is oscillatory.
, then Equation (1.1) is oscillatory.
Proof. Let 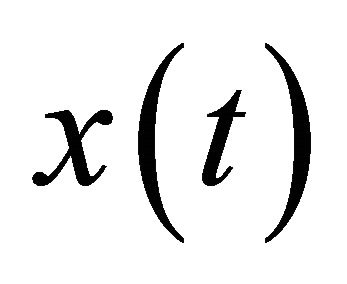 be a nonoscillatory solution of Equation (1.1). Then there exists a
be a nonoscillatory solution of Equation (1.1). Then there exists a  such that
such that  for all
for all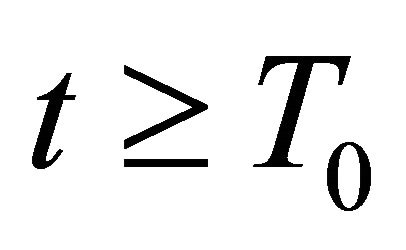 . Without loss of generality, we may assume that
. Without loss of generality, we may assume that  on interval
on interval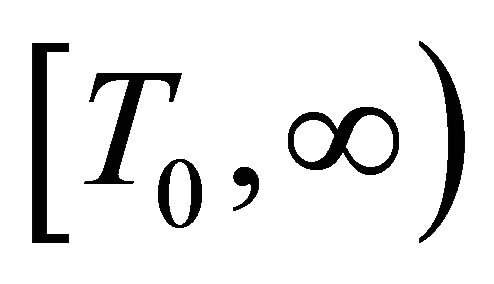 . A similar argument holds also for the case when
. A similar argument holds also for the case when 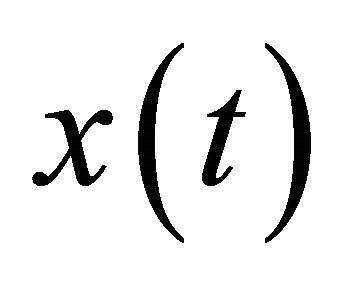 is eventually negative. As in [1], define a generalized Riccati transformation by
is eventually negative. As in [1], define a generalized Riccati transformation by
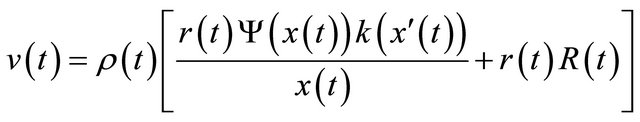 (2.6)
(2.6)
for all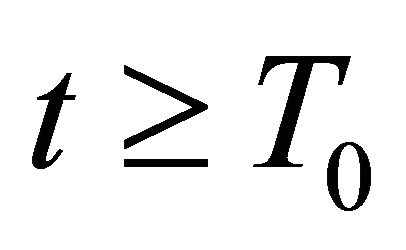 , then differentiating Equation (2.6) and using Equation (1.1), we obtain
, then differentiating Equation (2.6) and using Equation (1.1), we obtain
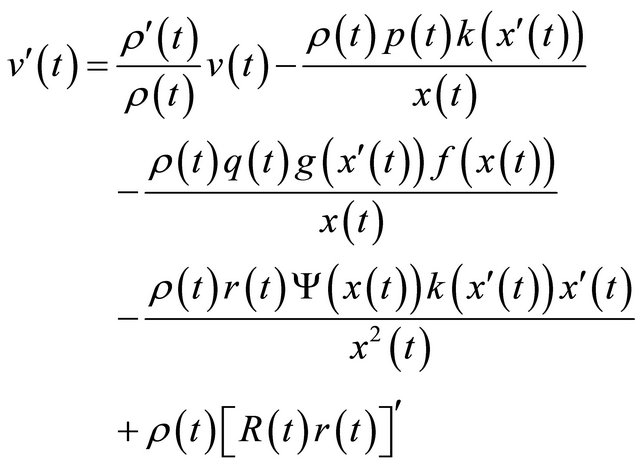 (2.7)
(2.7)
In view of (A1)-(A5), we get
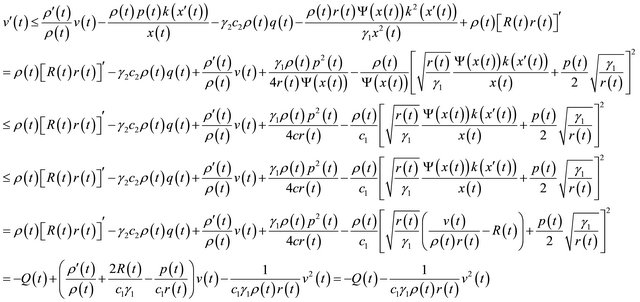
for all  with
with 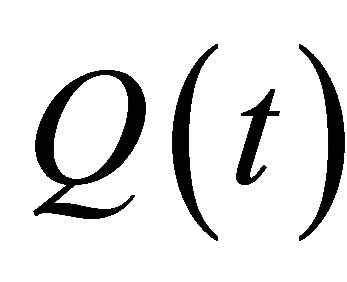 defined as above. Then we obtain
defined as above. Then we obtain
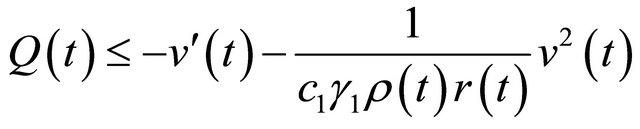 . (2.8)
. (2.8)
On multiplying Equation (2.8) (with t replaced by s) by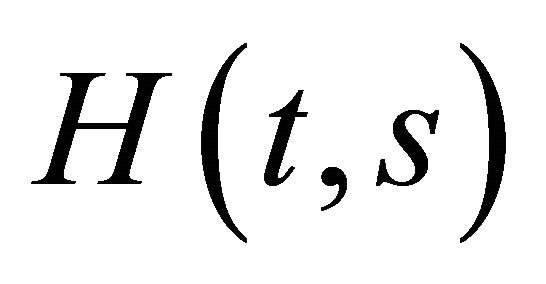 , integrating with respect to s from T to t for
, integrating with respect to s from T to t for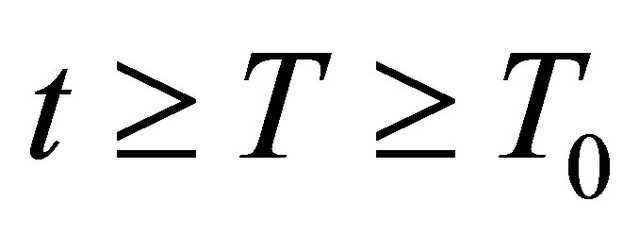 , using integration by parts and property 3), we get
, using integration by parts and property 3), we get
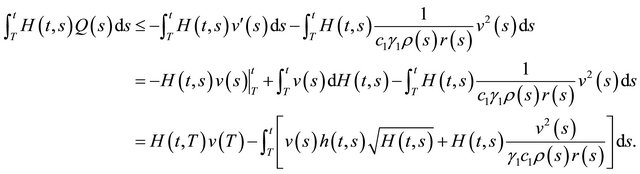
Then, for any 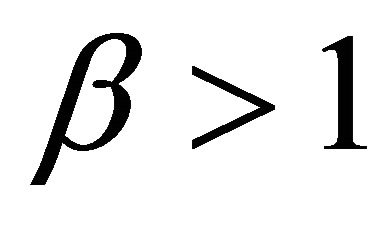

and, for all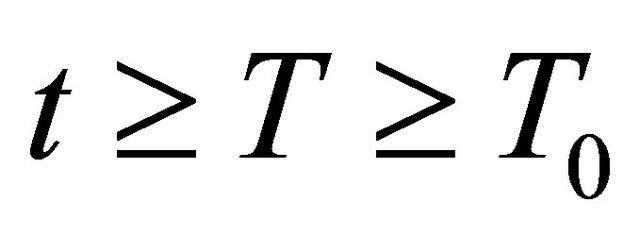 ,
,
 (2.9)
(2.9)
Furthermore,
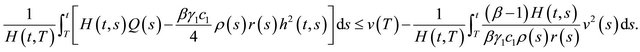
Now, it follows that
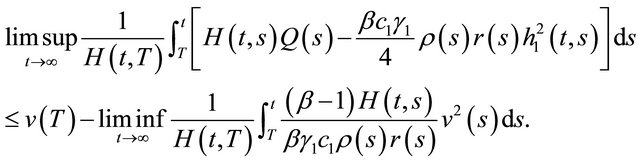 (2.10)
(2.10)
From (2.3) and (2.10), we have

for all  and
and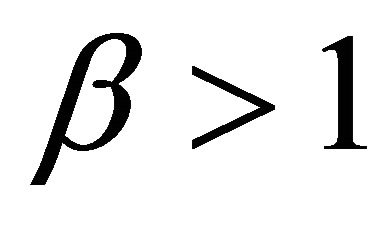 . Obviously,
. Obviously,
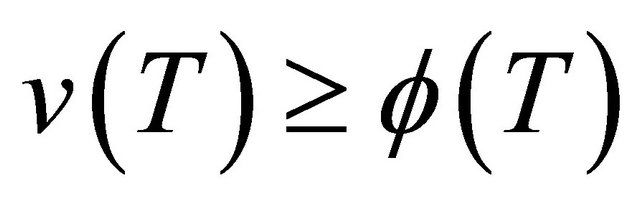 for all
for all  (2.11)
(2.11)
and
 (2.12)
(2.12)
Now, we can claim that
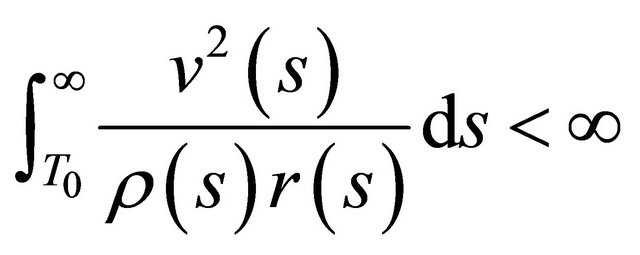 , (2.13)
, (2.13)
Otherwise,
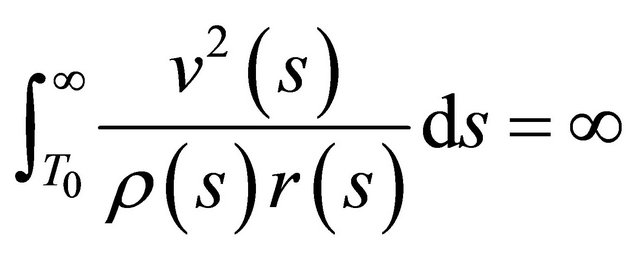 . (2.14)
. (2.14)
By (2.1), there exists a positive constant 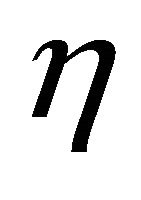 such that
such that
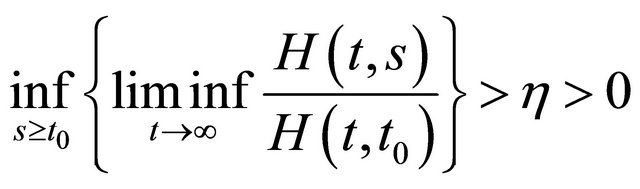 and there exists a
and there exists a 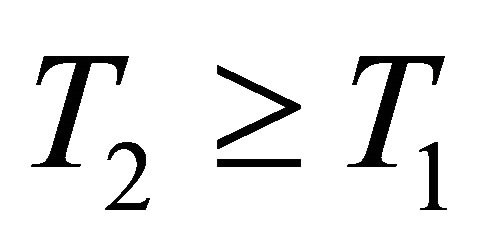 satisfying
satisfying
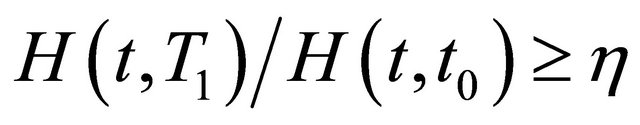 for all
for all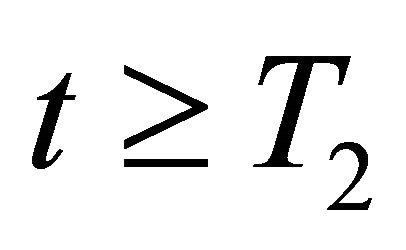 .
.
On the other hand, by (2.14) for any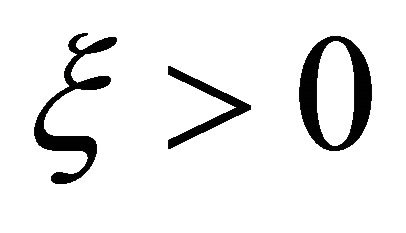 , there exists a
, there exists a 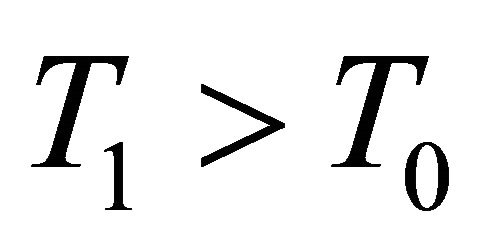 such that
such that
 for all
for all .
.
Using integration by parts, we obtain
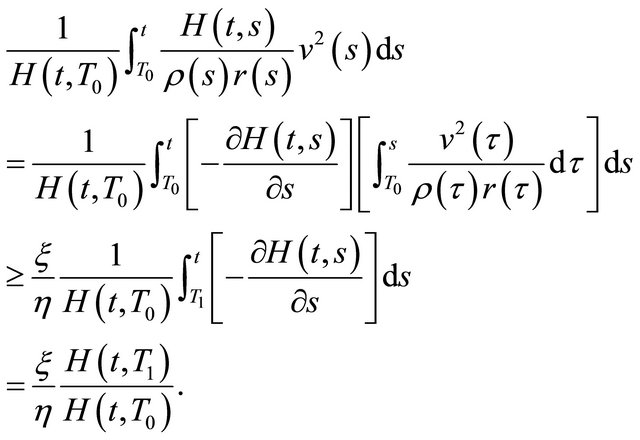
This implies that
 for all
for all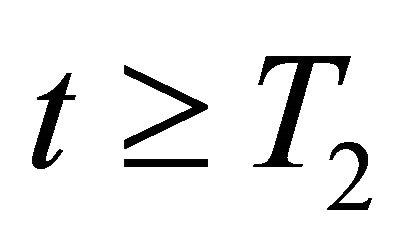 .
.
Since  is an arbitrary positive constant, we get
is an arbitrary positive constant, we get
 which contradicts (2.12), so (2.13) holds, and from (2.11)
which contradicts (2.12), so (2.13) holds, and from (2.11)
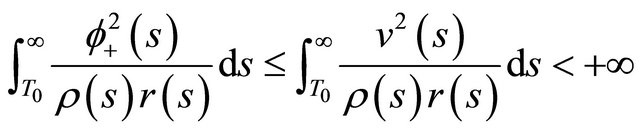 which contradicts (2.2), then Equation (1.1) is oscillatory.
which contradicts (2.2), then Equation (1.1) is oscillatory.
Now, we define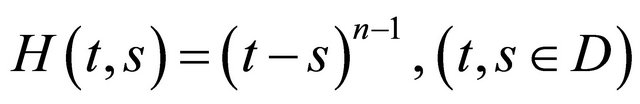 , here
, here  . Evidently,
. Evidently,  and
and
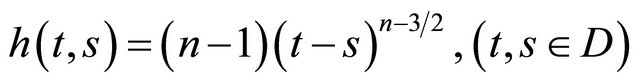 .
.
Thus, by Theorem 2.1, we obtain the following result.
Corollary 2.1. Let assumption (A1)-(A5) be fulfilled. Suppose that (2.2) holds. If there exist functions 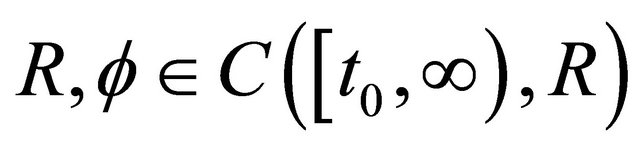 such that
such that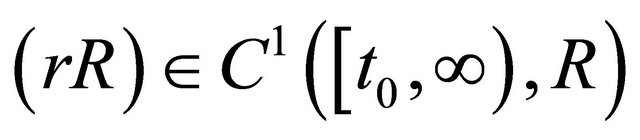 ,
,
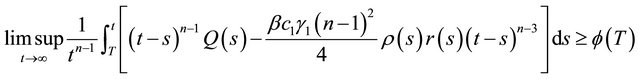 where
where 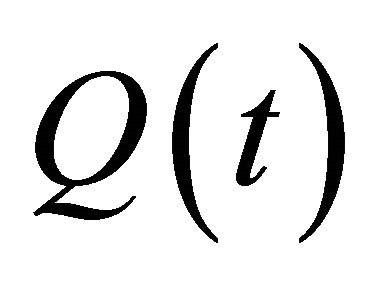 and
and  are defined as in Theorem 2.1, then Equation (1.1) is oscillatory.
are defined as in Theorem 2.1, then Equation (1.1) is oscillatory.
Example 2.1. Consider the nonlinear damped differential equation
 .
.
where 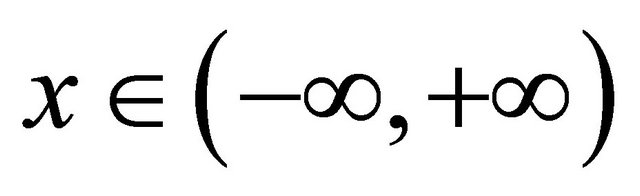 and
and ,
, 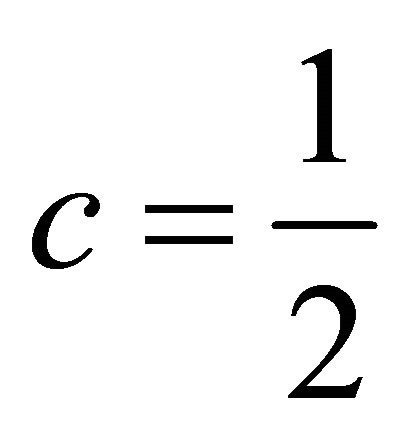 ,
,  ,
,
 .
.
The assumptions (A1)-(A5) hold. If we take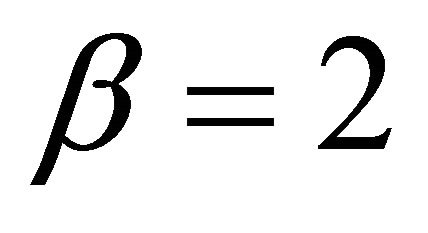 ,
,  and
and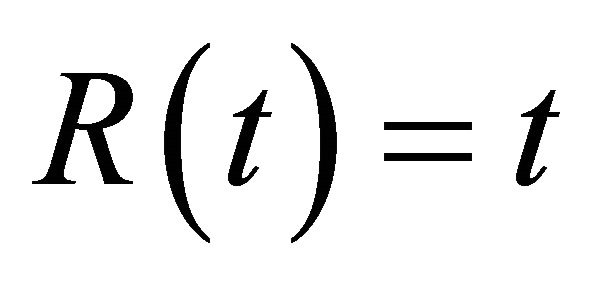 , then
, then , and
, and
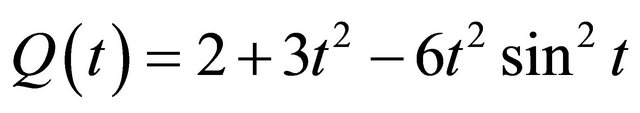 .
.
A direct computation yields that the conditions of Corallary 2.1 are satisfied, Equation (1.1) is oscillatory.
As a direct consequence of Theorem 2.1, we get the following result.
Corollary 2.2. In Theorem 2.1, if condition (2.3) is replaced by
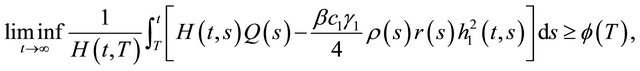
where 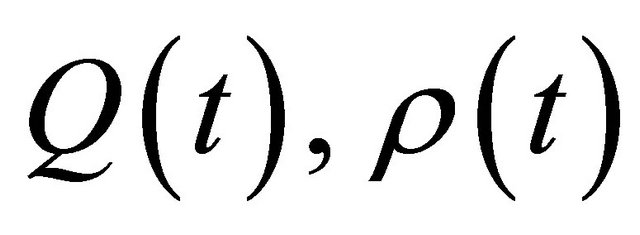 and
and 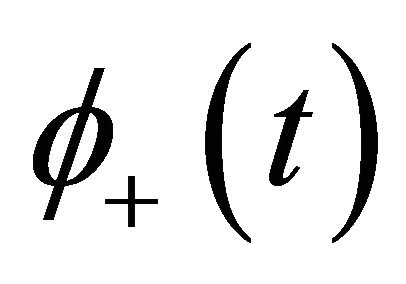 are the same as in Theorem 2.1, then Equation (1.1) is oscillatory.
are the same as in Theorem 2.1, then Equation (1.1) is oscillatory.
Theorem 2.2. Let assumption (A1)-(A5) be fulfilled. For some , if there exist functions
, if there exist functions
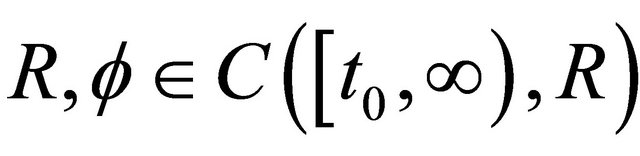 such that
such that
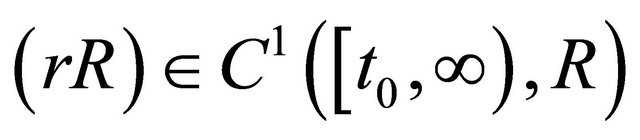
and
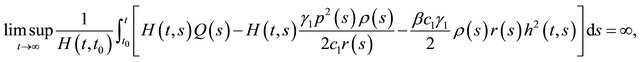
where 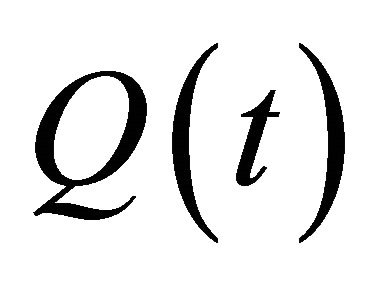 is the same as in Theorem 2.1,
is the same as in Theorem 2.1, 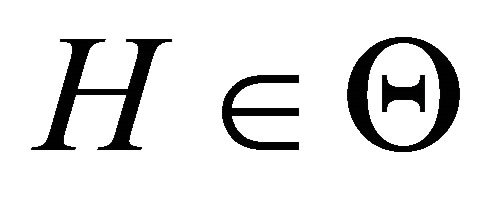 and
and
 (2.16)
(2.16)
Then Equation (1.1) is oscillatory.
Proof. Let 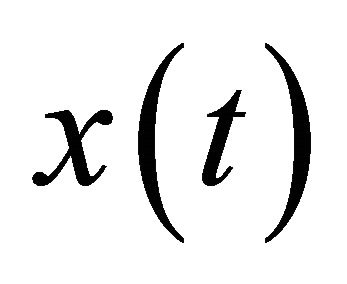 be a nonoscillatory solution of Equation (1.1). Then there exists a
be a nonoscillatory solution of Equation (1.1). Then there exists a 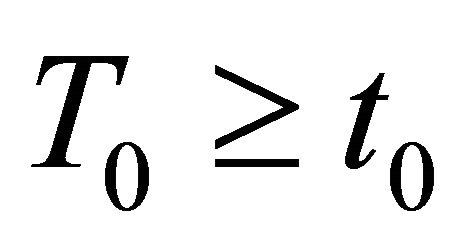 such that
such that 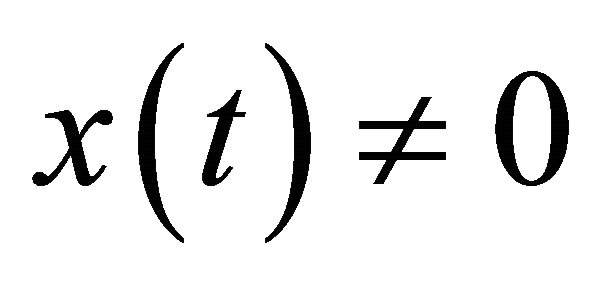 for all
for all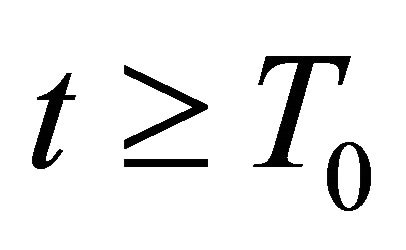 . Without loss of generality, we may assume that
. Without loss of generality, we may assume that  on interval
on interval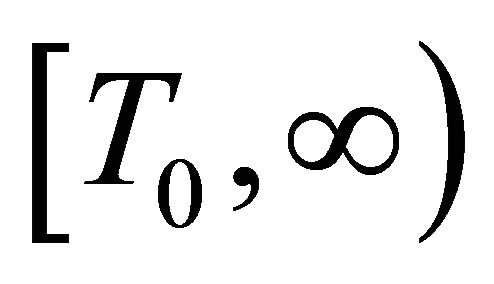 . A similar argument holds also for the case when
. A similar argument holds also for the case when 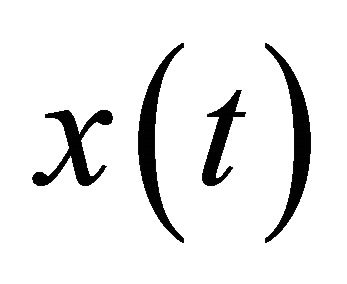 is eventually negative.
is eventually negative.
Define the function 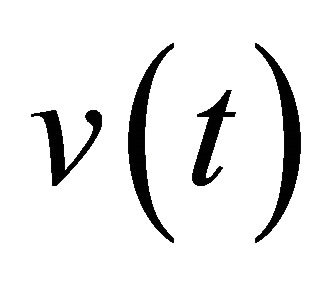 as in (2.6). Using (A1)-(A5) and (2.7), we have
as in (2.6). Using (A1)-(A5) and (2.7), we have
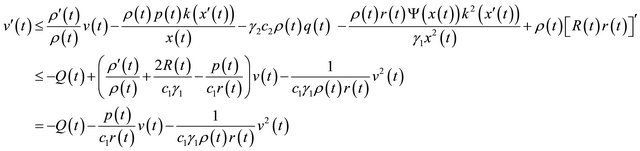 (2.17)
(2.17)
where  is the same as in Theorem 2.1. On the other hand, since the inequality
is the same as in Theorem 2.1. On the other hand, since the inequality
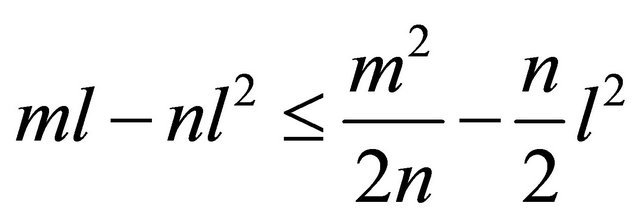
holds for all 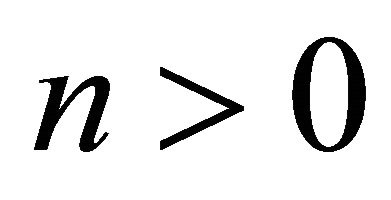 and
and . Let
. Let
 we get from (2.17) that
we get from (2.17) that
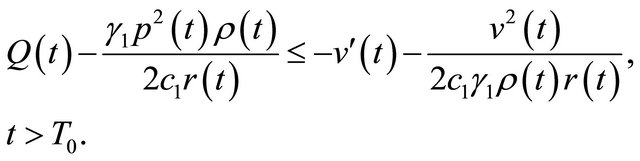 (2.18)
(2.18)
On multiplying (2.18) (with t replaced by s) by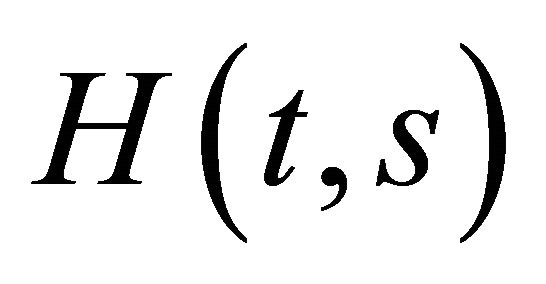 , integrating with respect to s from T to t for
, integrating with respect to s from T to t for 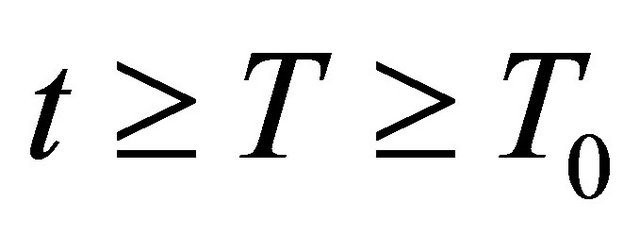 and
and , using integration by parts and property 3), we get
, using integration by parts and property 3), we get
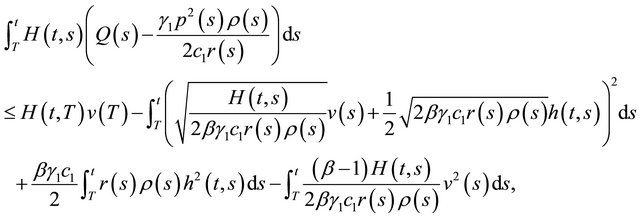
This implies that
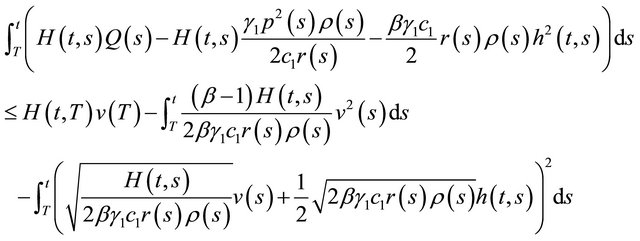
Using the properties of , we have
, we have

Therefore,
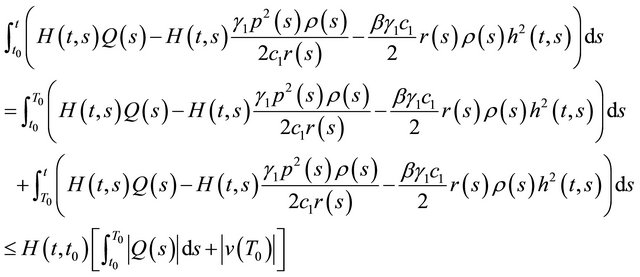
for all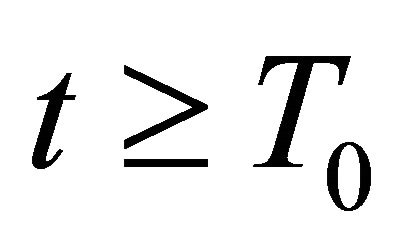 , and so
, and so
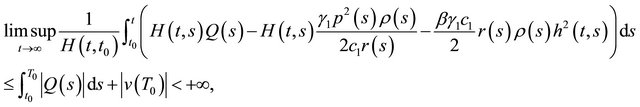
which contradicts with the assumption (2.15). This completes the proof of Theorem 2.2.
Let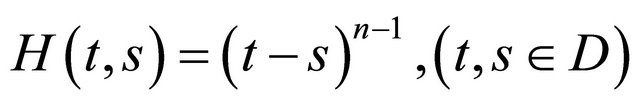 , from Theorem 2.2, we obtain the next result.
, from Theorem 2.2, we obtain the next result.
Corollary 2.3. Let assumption (A1)-(A5) be fulfilled. If there exist functions  such that
such that
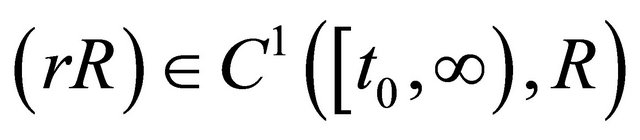 and
and

holds for some integer 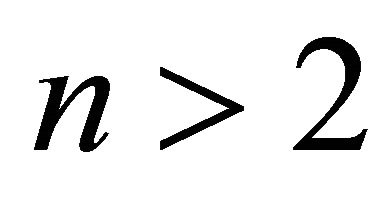 and
and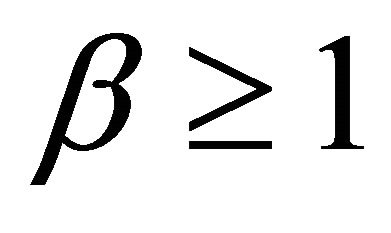 , where
, where 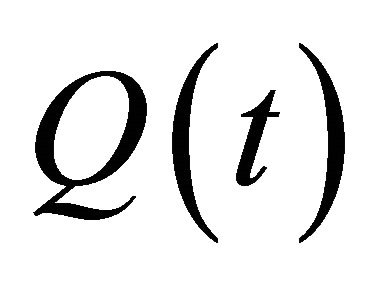 and
and 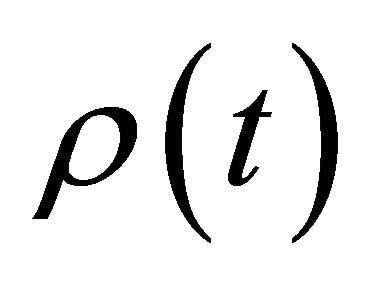 are defined as in Theorem 2.2, then Equation (1.1) is oscillatory.
are defined as in Theorem 2.2, then Equation (1.1) is oscillatory.
Example 2.2. Consider the nonlinear damped differential equation
 (2.19)
(2.19)
Evidently, for all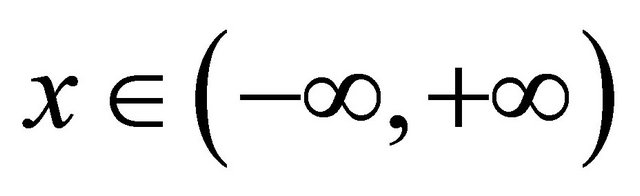 ,
,  and
and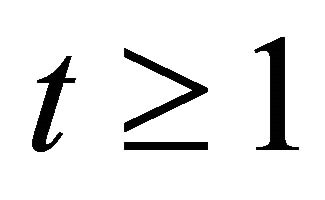 , we have
, we have
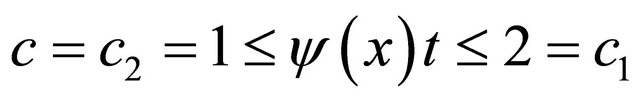 and
and
 .
.
Let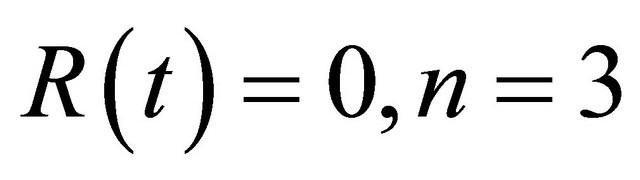 , then
, then
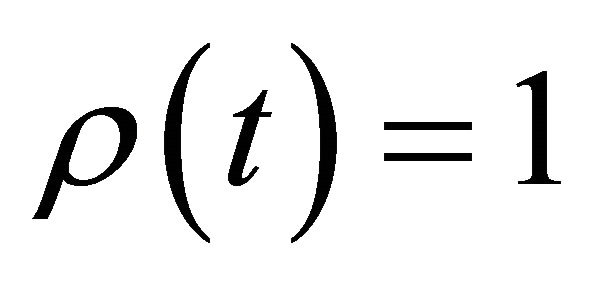 and
and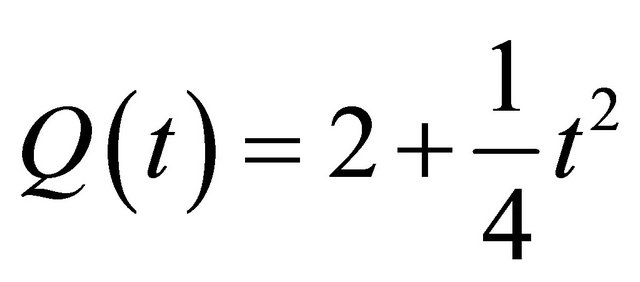 .
.

Therefore, Equation (2.19) is oscillatory by Corallary 2.3.
Theorem 2.3. Let assumption (A1)-(A5) be fulfilled and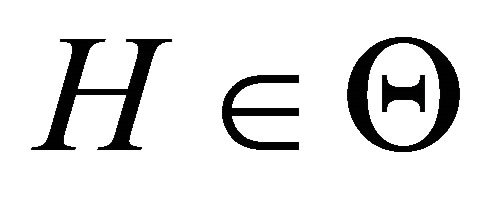 . If there exist functions
. If there exist functions 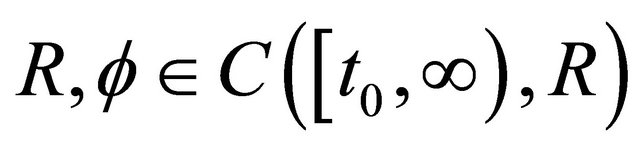
such that (2.1) holds and , and for all
, and for all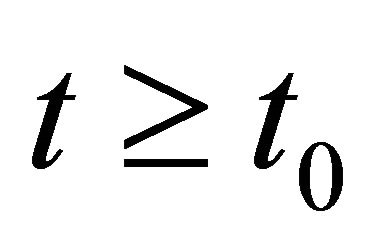 , any
, any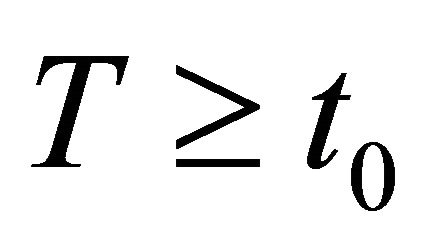 , and for some
, and for some ,
,
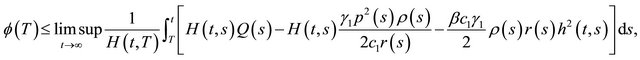 (2.20)
(2.20)
where  and
and  are the same as in Theorem 2.2 and
are the same as in Theorem 2.2 and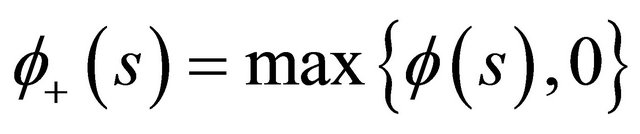 . If (2.2) is satisfied, then Equation (1.1) is oscillatory.
. If (2.2) is satisfied, then Equation (1.1) is oscillatory.
Proof. The proof of this theorem is similar to that of Theorem 2.1 and hence is omitted.
Theorem 2.4. Let all assumptions of Theorem 2.3 be fulfilled except the condition (2.20) be replaced by

then Equation (1.1) is oscillatory.
Remark 2.1. If we take , then the condition
, then the condition 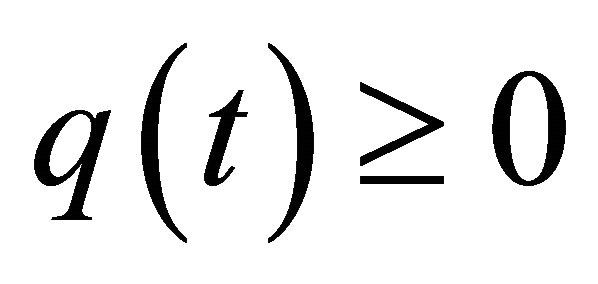 is not necessary.
is not necessary.
Remark 2.2. If we take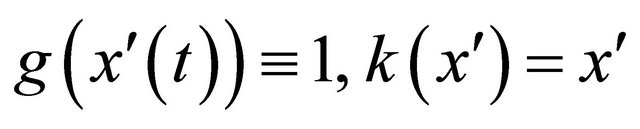 , then Theorem 2.3 and 2.4 reduce to Theorem 9 and 10 of [21] with
, then Theorem 2.3 and 2.4 reduce to Theorem 9 and 10 of [21] with , respectively.
, respectively.
Remark 2.3. If replace (A5) and (2.6) by 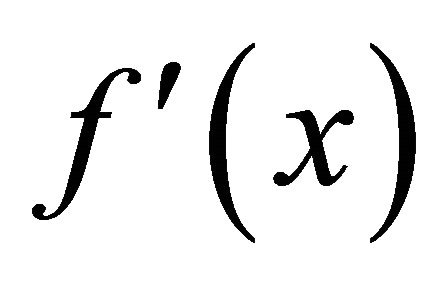 exists,
exists, 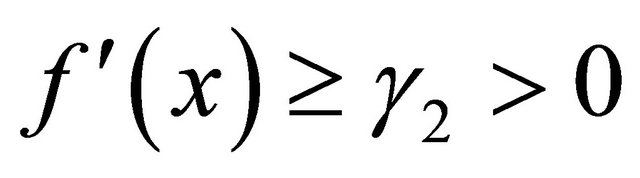 for
for 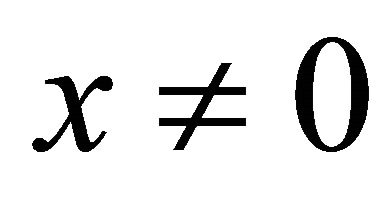 and define
and define
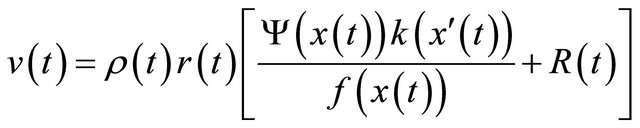
respectively, we can obtain similar oscillation results that are derived in the present paper.
3. Acknowledgements
This work was supported by the National Natural Science Foundation of China (11071011), the Funding Project for Academic Human Resources Development in Institutions of Higher Learning under the Jurisdiction of Beijing Municipality (PHR201107123), the Plan Project of Science and Technology of Beijing Municipal Education Committee (KM201210016007) and the Natural Science Foundation of Beijing University of Civil Engineering and Architecture (10121907).
REFERENCES
- Q. R. Wang, “Oscillation Criteria for Nonlinear Second Order Damped Differential Equations,” Acta Mathematica Hungarica, Vol. 102, No. 1-2, 2004, pp. 117-139.
- R. P. Agarwal and S. R. Grace, “On the Oscillation of Certain Second Order Differential Equations,” Georgian Mathematical Journal, Vol. 7, No. 2, 2000, pp. 201-213.
- B. Ayanlar and A. Tiryaki, “Oscillation Theorems for Nonlinear Second Order Differential Equations with Damping,” Acta Mathematica Hungarica, Vol. 89, No. 1-2, 2000, pp. 1-13. doi:10.1023/A:1026716923088
- S. R. Grace, “Oscillation Theorems for Nonlinear Differential Equations of Second Order,” Journal of Mathematical Analysis and Applications, Vol. 171, No. 1, 1992, pp. 220-241. doi:10.1016/0022-247X(92)90386-R
- I. V. Kamenev, “An Integral Criterion for Oscillation of Linear Differential Equations of Second Order,” Matematicheskie Zametki, Vol. 23, No. 2, 1978, pp. 136-138.
- M. Kirane and Y. V. Rogovchenko, “On Oscillation of Nonlinear Second Order Differential Equation with Damping Term,” Applied Mathematics and Computation, Vol. 117, No. 2-3, 2001, pp. 177-192. doi:10.1016/S0096-3003(99)00172-1
- M. Kirane and Y. V. Rogovchenko, “Oscillation Results for a Second Order Damped Differential Equation with Nonmonotonous Nonlinearity,” Journal of Mathematical Analysis and Applications, Vol. 250, No. 1, 2000, pp. 118-138. doi:10.1006/jmaa.2000.6975
- H. J. Li, “Oscillation Criteria for Second Order Linear Differential Equations,” Journal of Mathematical Analysis and Applications, Vol. 194, No. 1, 1995, pp. 217-234. doi:10.1006/jmaa.1995.1295
- W. T. Li, “Oscillation of Certain Second-Order Nonlinear Differential Equations,” Journal of Mathematical Analysis and Applications, Vol. 217, No. 1, 1998, pp. 1-14. doi:10.1006/jmaa.1997.5680
- Ch. G. Philos, “Oscillation Theorems for Linear Differential Equations of Second Order,” Archiv der Mathematik, Vol. 53, No. 5, 1989, pp. 482-492. doi:10.1007/BF01324723
- Y. V. Rogovchenko, “Oscillation Theorems for SecondOrder Equations with Damping,” Nonlinear Analysis: Theory, Methods & Applications, Vol. 41, No. 7-8, 2000, pp. 1005-1028. doi:10.1016/S0362-546X(98)00324-1
- Y. V. Rogovchenko, “On Oscillation of a Second Order Nonlinear Delay Differential Equation,” Funkcialaj Ekvacioj, Vol. 43, 2000, pp. 1-29.
- Y. V. Rogovchenko, “Oscillation Criteria for Second Order Nonlinear Perturbed Differential Equations,” Journal of Mathematical Analysis and Applications, Vol. 215, No. 2, 1997, pp. 334-357. doi:10.1006/jmaa.1997.5595
- Q. R. Wang, “Oscillation and Asymptotics for SecondOrder Half-Linear Differential Equations,” Applied Mathematics and Computation, Vol. 122, No. 2, 2001, pp. 253-266. doi:10.1016/S0096-3003(00)00056-4
- Q. R. Wang, “Oscillation Criteria for Even Order Nonlinear Damped Differential Equations,” Acta Mathematica Hungarica, Vol. 95, No. 23, 2002, pp. 169-178. doi:10.1023/A:1015676519998
- A. Tiryaki and A. Zafer, “Oscillation Criteria for Second order Nonlinear Differential Equations with Damping,” Turkish Journal of Mathematics, Vol. 24, 2000, pp. 185- 196.
- J. Yan, “Oscillation Theorems for Second Order Linear Differential Equations with Damping,” Proceedings of the American Mathematical Society, Vol. 98, No. 2, 1986, pp. 276-282. doi:10.1090/S0002-9939-1986-0854033-4
- P. Hartman, “On Non-Oscillatory Linear Differential Equations of Second Order,” American Journal of Mathematics, Vol. 74, No. 2, 1952, pp. 389-400. doi:10.2307/2372004
- A. Wintner, “A Criterion of Oscillatory Stability,” Quarterly of Applied Mathematics, Vol. 7, 1949, pp. 115-117.
- Y. V. Rogovchenko and F. Tuncay, “Oscillation Criteria for Second-Order Nonlinear Differential Equations with Damping,” Nonlinear Analysis, Vol. 69, No. 1, 2008, pp. 208-221. doi:10.1016/j.na.2007.05.012
- Y. V. Rogcvchenko and F. Tuncay, “Oscillation Theorems for a Class of Second Order Nonlinear Differential Equations with Damping,” Taiwanese Journal of Mathematics, Vol. 13, No. 6B, 2009, pp. 1909-1928.
- X. J. Wang and G. H. Song, “Oscillation Criteria for a Second-Order Nonlinear Damped Differential Equation,” International Journal of Information and Systems Sciences, Vol. 7, No. 1, 2011, pp. 73-82.

