Advances in Pure Mathematics
Vol.3 No.1(2013), Article ID:27361,6 pages DOI:10.4236/apm.2013.31012
The Zeros of a Certain Homogeneous Difference Polynomials of Meromorphic Functions*
1Department of Mathematics, Southwest University of Science and Technology, Mianyang, China
2Department of Material Science and Engineer, Southwest University of Science and Technology, Mianyang, China
Email: luqiankuo1965@hotmail.com, liaoql@swust.edu.cn
Received October 17, 2012; revised November 26, 2012; accepted December 4, 2012
Keywords: Meromorphic Functions; Zeros; Homogeneous Difference Polynomials
ABSTRACT
Let 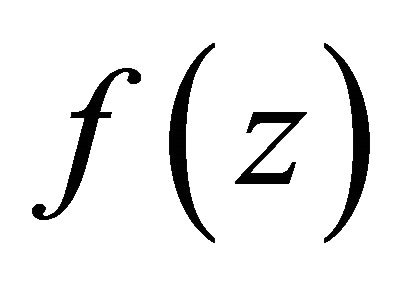 be a function transcendental and meromorphic in the plane of growth order less than 1. This paper focuses on discussing and estimating the number of the zeros of a certain homogeneous difference polynomials of degree k in
be a function transcendental and meromorphic in the plane of growth order less than 1. This paper focuses on discussing and estimating the number of the zeros of a certain homogeneous difference polynomials of degree k in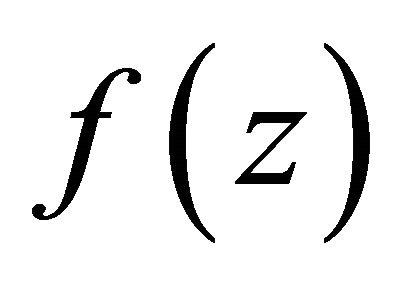 , and obtains that this certain homogeneous difference polynomials has infinitely many zeros.
, and obtains that this certain homogeneous difference polynomials has infinitely many zeros.
1. Introduction and the Main Result
Let 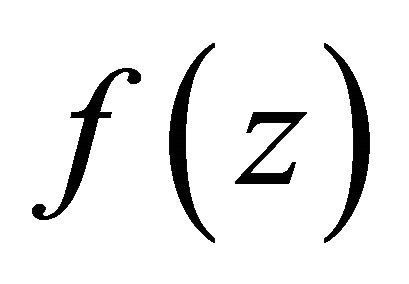 be a function transcendental and meromorphic in the plane. In what follow, we denote the convergence exponent of the zeros of
be a function transcendental and meromorphic in the plane. In what follow, we denote the convergence exponent of the zeros of 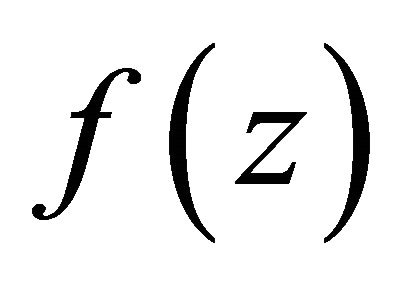 by
by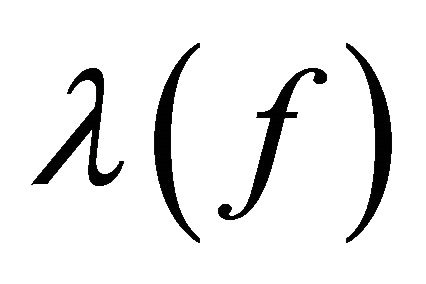 , the growth order of
, the growth order of 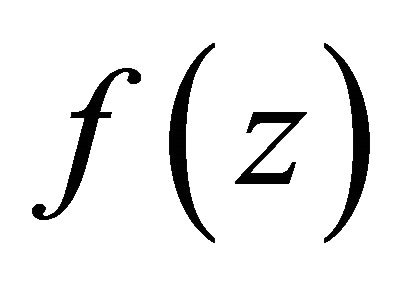 by
by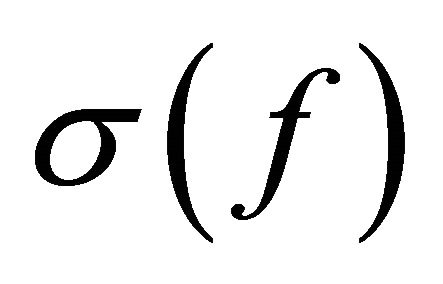 , and the lower order of
, and the lower order of 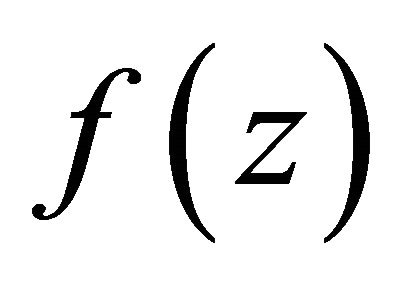 by
by .
.
Following Whittaker [1], define the forward differences to be k times iteration  of the difference operator
of the difference operator![]() , that is,
, that is,
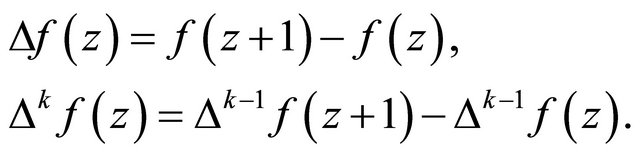 (1.1)
(1.1)
Recently, a number of papers research on complex difference equations and differences analogues of Nevanlinna’s theory [2-6]. Bergweiler and Langley [7] firstly investigated the existence of zeros of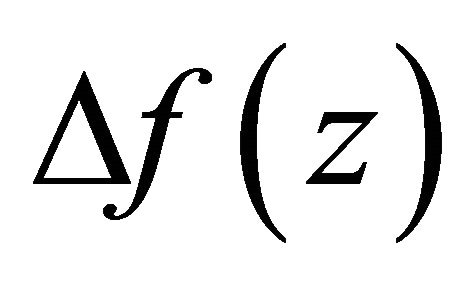 , and obtained a result as follow.
, and obtained a result as follow.
Theorem 1.1. Let f be a function transcendental and meromorphic of lower order 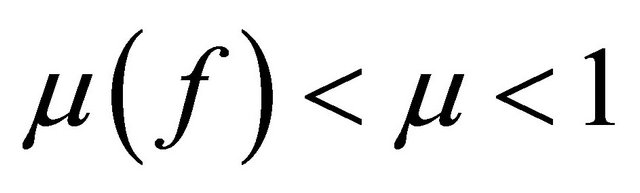 in the plane. Let
in the plane. Let  be such that at most finitely many poles
be such that at most finitely many poles  of
of 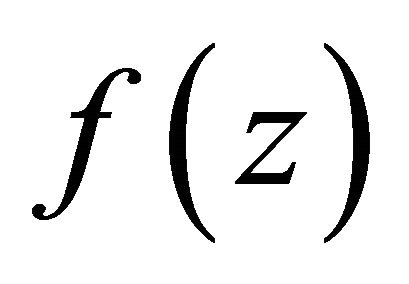 satisfy
satisfy . Then
. Then 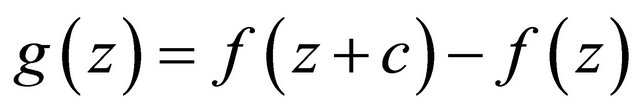 has infinitely many zeros.
has infinitely many zeros.
In 2008, Z. X. Chen and K. H. Shon [8].
Theorem 1.2. Let 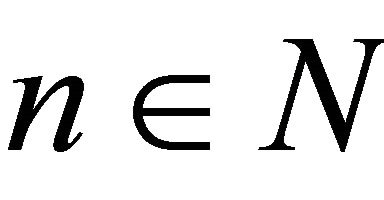 and f be a function transcendental and meromorphic of lower order
and f be a function transcendental and meromorphic of lower order  in the plane. Let
in the plane. Let  and a set
and a set 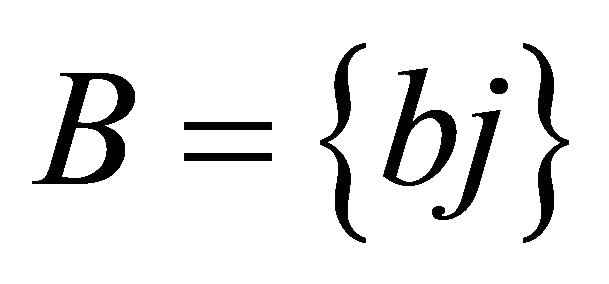 consist of all poles of
consist of all poles of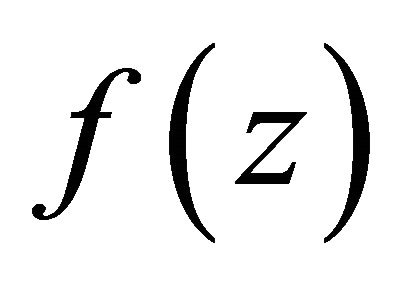 , such that
, such that
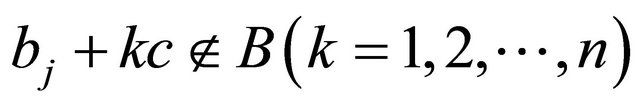
at most except finitely many exceptions. Then 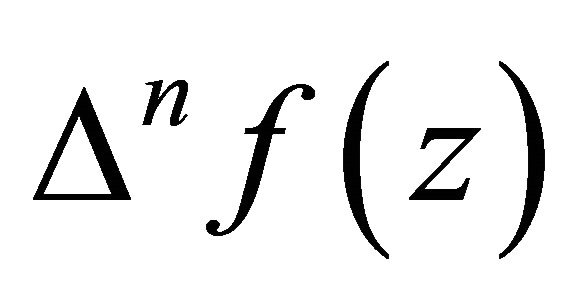 has infinitely many zeros.
has infinitely many zeros.
In 2009, Z. X. Chen and K. H. Shon [9] continue to investigate the existence of the zeros of the difference polynomials defined as follows
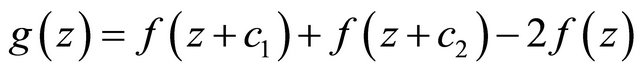 (1.2)
(1.2)
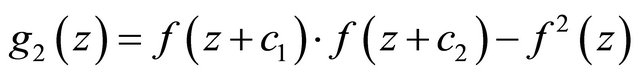 (1.3)
(1.3)
and obtained two results.
Theorem 1.3. Let f be a function transcendental and meromorphic of growth order , and
, and 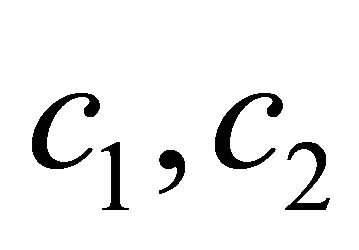 be two complex numbers, such that
be two complex numbers, such that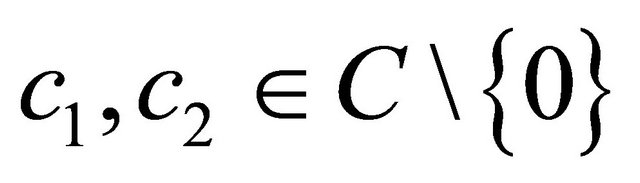 , and
, and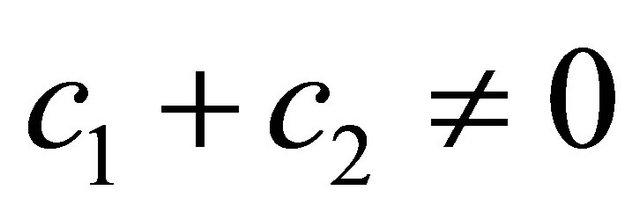 . If
. If 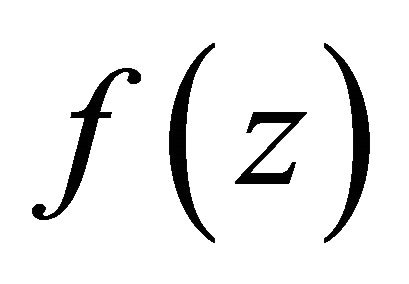 has at most finitely many poles
has at most finitely many poles  satisfying
satisfying 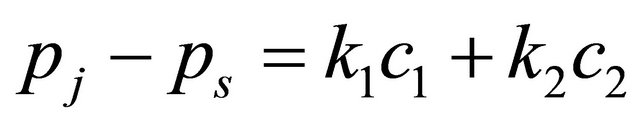
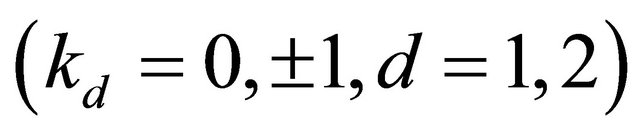 , then
, then  has infinitely many zeros, and
has infinitely many zeros, and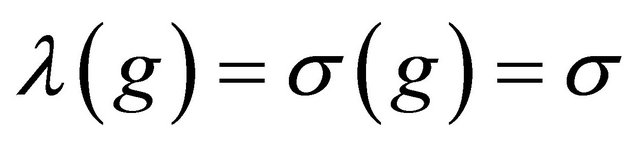 .
.
In particular, if 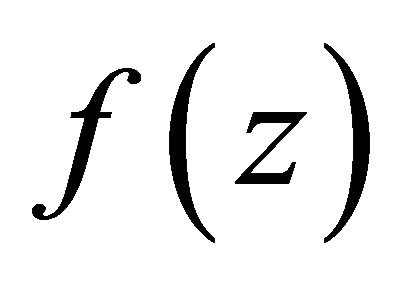 has at most finitely many zeros
has at most finitely many zeros 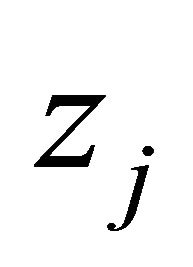 satisfying
satisfying , then
, then 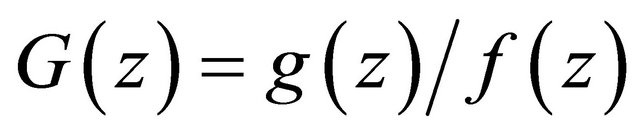 has also infinitely many zeros, and
has also infinitely many zeros, and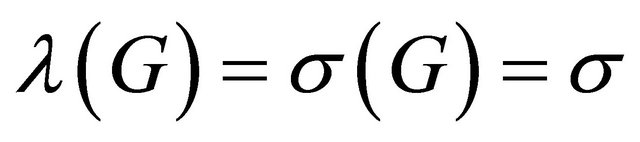 .
.
Theorem 1.4. Let  satisfy the conditions in Theorem 1.3, If
satisfy the conditions in Theorem 1.3, If 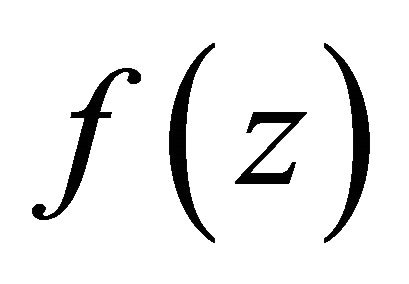 has at most finitely many poles
has at most finitely many poles 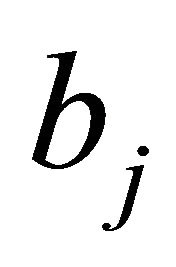 satisfying
satisfying
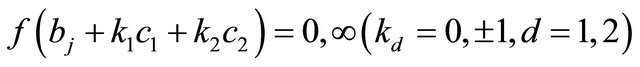 then
then 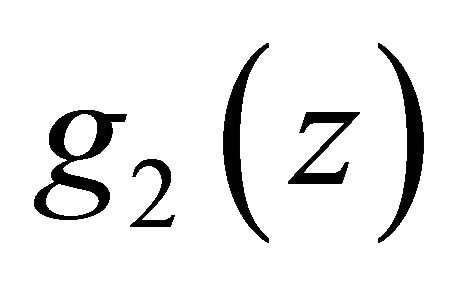 has infinitely many zeros, and
has infinitely many zeros, and  .
.
In particular, if 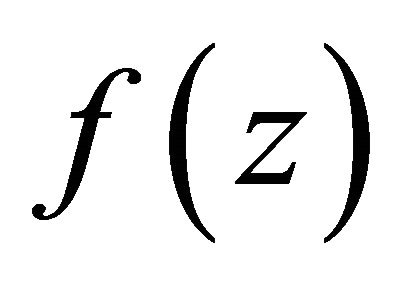 has at most finitely many zeros
has at most finitely many zeros 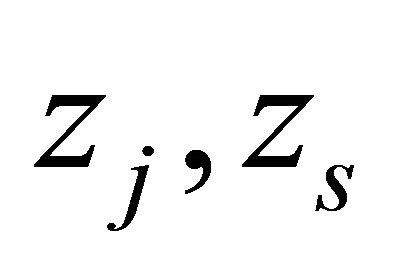 such that
such that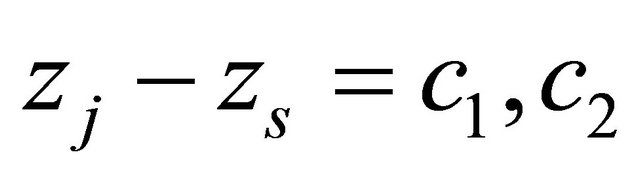 , then
, then 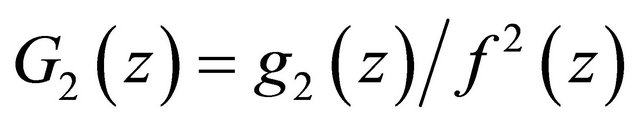 has also infinitely many zeros, and
has also infinitely many zeros, and
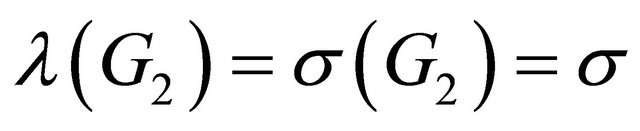 .
.
It is not difficult to understand that  defined by (1.2) is more general difference polynomials than
defined by (1.2) is more general difference polynomials than  or
or 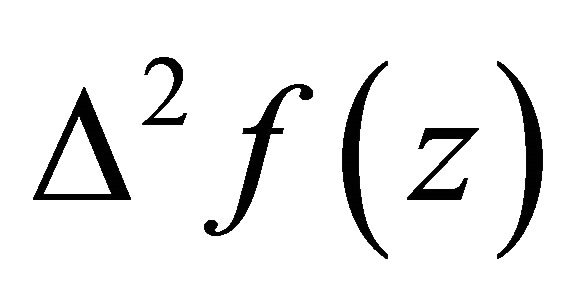 and Theorem 1.3 extends Theorem 1.1. Therefore, we pose naturally one question whether more general difference polynomials than
and Theorem 1.3 extends Theorem 1.1. Therefore, we pose naturally one question whether more general difference polynomials than  defined by (1.3) has also infinitely many zeros. In this paper, we focus on research a certain homogeneous difference polynomials and affirm to answer this problem.
defined by (1.3) has also infinitely many zeros. In this paper, we focus on research a certain homogeneous difference polynomials and affirm to answer this problem.
Theorem 1.5. Suppose that k is a positive integer,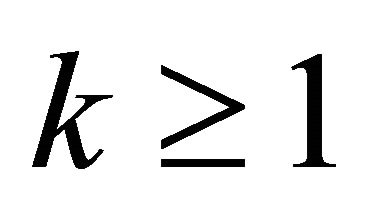 . Let
. Let 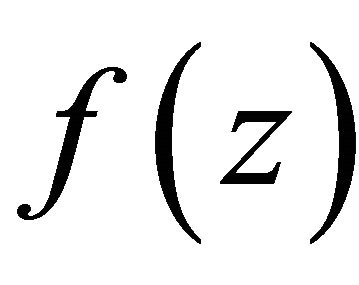 be a function transcendental and meromorphic of growth order
be a function transcendental and meromorphic of growth order , and there exists k complex numbers
, and there exists k complex numbers 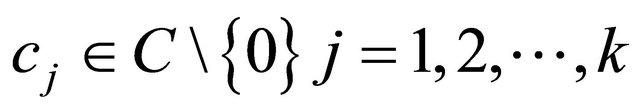 such that
such that
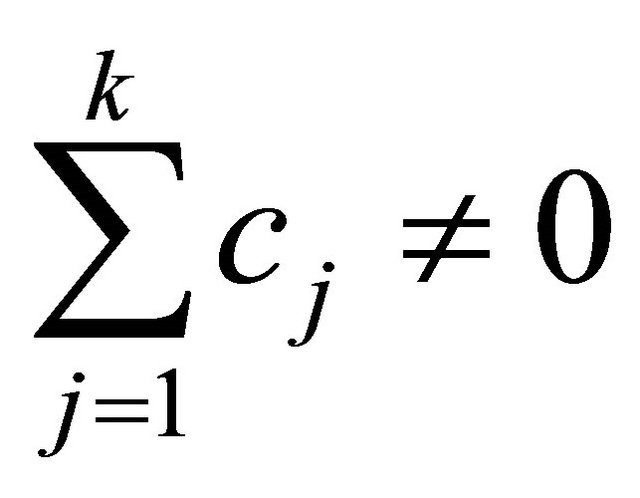 . If
. If  has at most finitely many poles bj
has at most finitely many poles bj
satisfying

Then 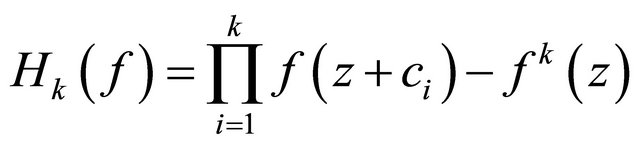 has infinitely many zeros, and
has infinitely many zeros, and .
.
In particular, if 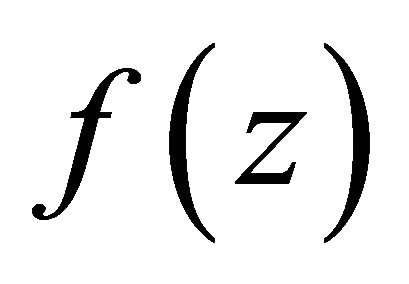 has at most finitely many zeros
has at most finitely many zeros 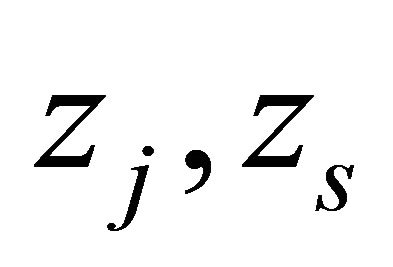 satisfying
satisfying , then
, then 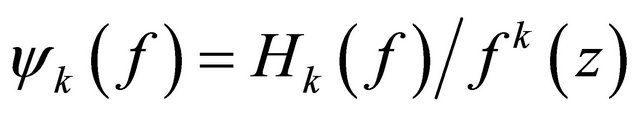 has also infinitely many zeros, and
has also infinitely many zeros, and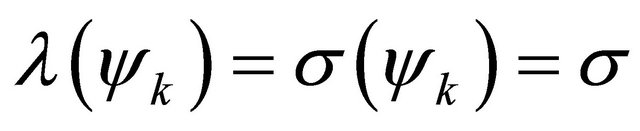 .
.
2. Lemmas
Lemma 2.1. (see [7]) Let f be a function transcendental and meromorphic in the plane of growth order less than 1, and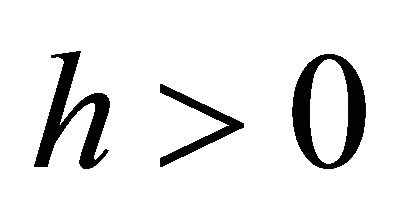 . Then there exists an
. Then there exists an 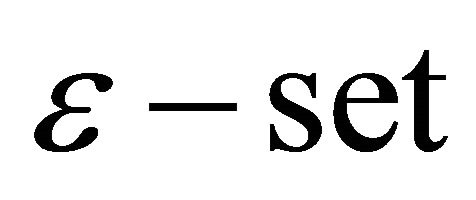 E such that
E such that
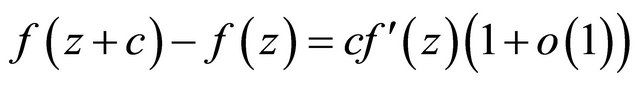 , (2.1)
, (2.1)
as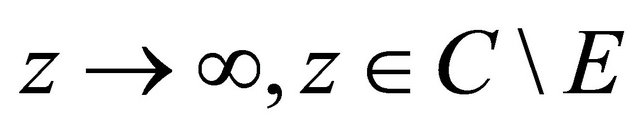 , uniformly in
, uniformly in ![]() for
for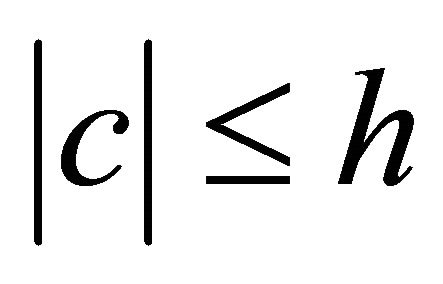 .
.
Lemma 2.2. (see [7]) Let 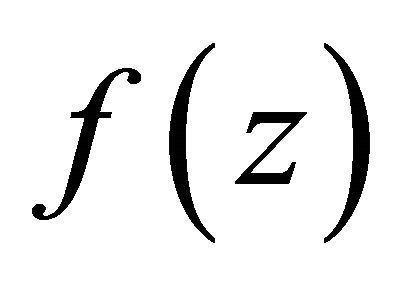 be a function transcendental and meromorphic in the plane of lower order
be a function transcendental and meromorphic in the plane of lower order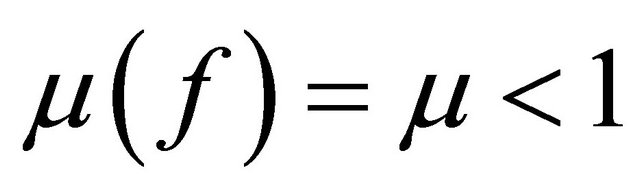 . Then there exists arbitrarily large R with the following properties. First,
. Then there exists arbitrarily large R with the following properties. First,
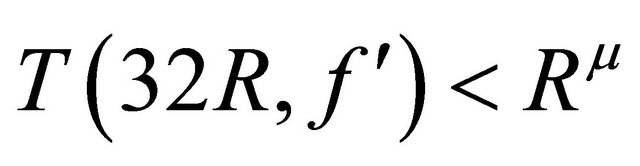 . (2.2)
. (2.2)
Second, there exists a set  of linear measure
of linear measure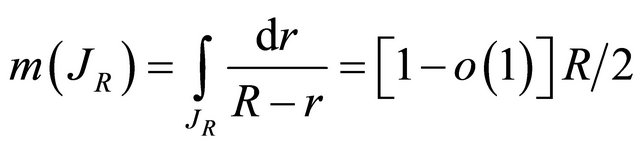 , such that for
, such that for
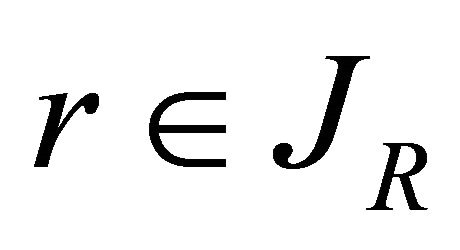 ,
,
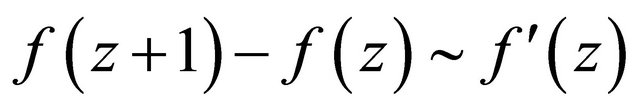 (2.3)
(2.3)
on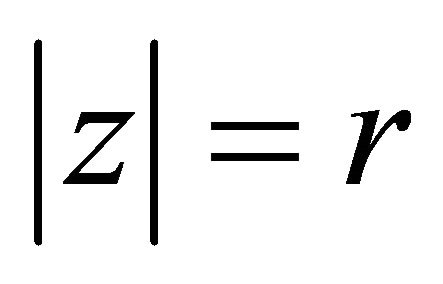 .
.
Lemma 2.3. Let 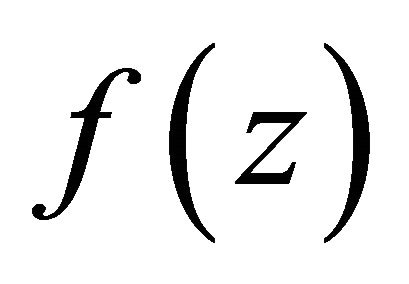 be a function transcendental and meromorphic in the plane with growth order
be a function transcendental and meromorphic in the plane with growth order
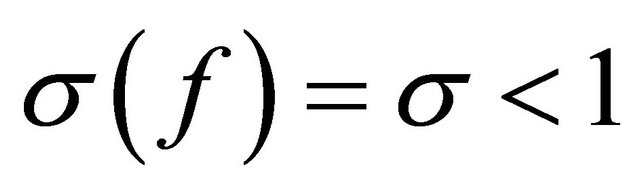 . Supposed that
. Supposed that . If the homogeneous difference polynomials
. If the homogeneous difference polynomials
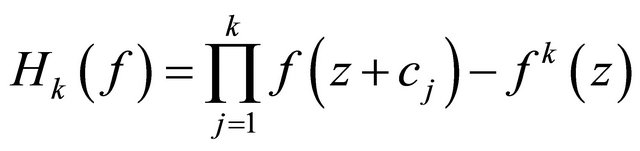 or quotient of difference polynomials
or quotient of difference polynomials

is rational functions, then 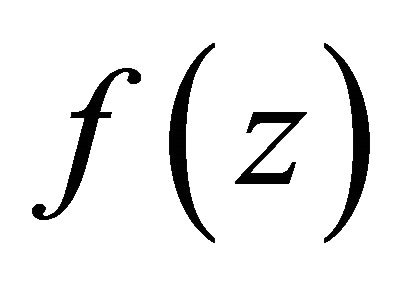 has at most finite many poles.
has at most finite many poles.
Proof. Without loss of generality, we assume that c1 = 1. Because that the homogeneous difference polynomials 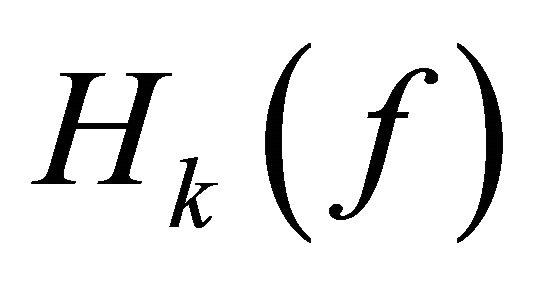 is rational, there exists a rational functions
is rational, there exists a rational functions  such that
such that
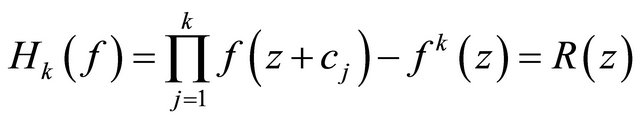 . (2.4)
. (2.4)
Set
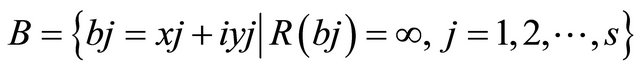 and
and
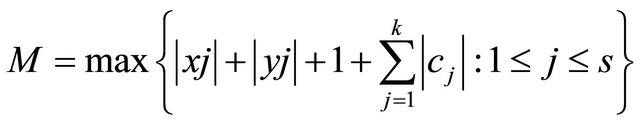 .
.
So there exists no poles of  in the domain
in the domain
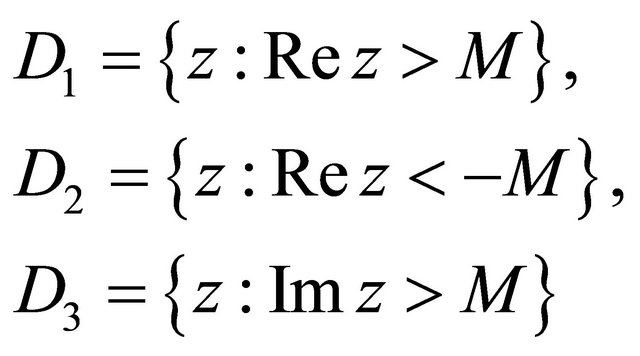
and
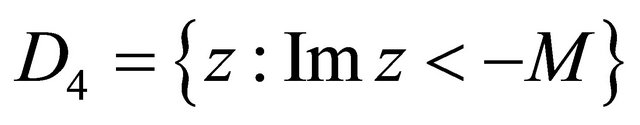 .
.
Now we complete the proof of the conclusion that  has at most finite.
has at most finite.
Now we complete the proof of the conclusion that 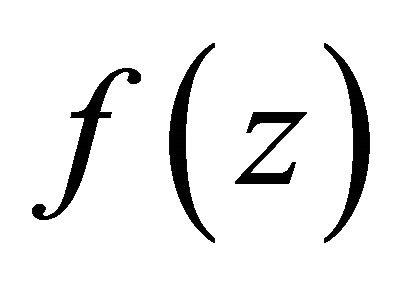 has at most finite many poles. Suppose not, there exists one domain Dj, for example D1, in which
has at most finite many poles. Suppose not, there exists one domain Dj, for example D1, in which 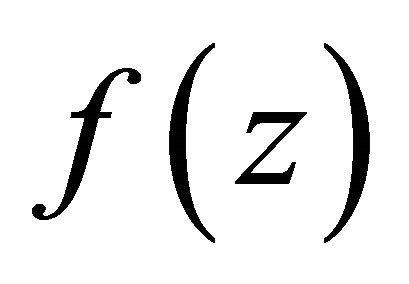 has infinitely many poles. We assume that the set
has infinitely many poles. We assume that the set 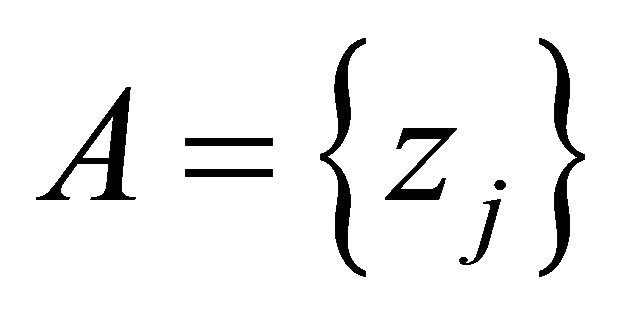 consists of all poles of
consists of all poles of 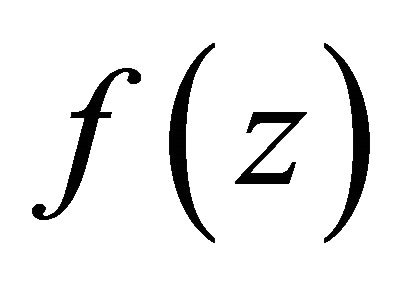 in D1 and
in D1 and 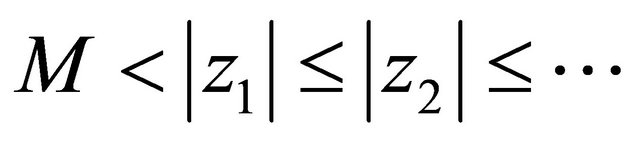 and divide it into two cases:
and divide it into two cases:
Case 1. There exists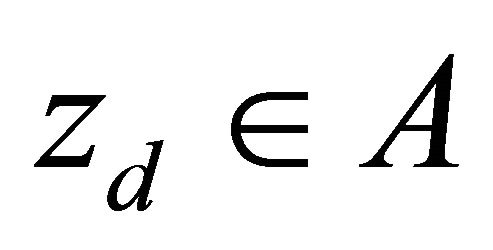 , such that for an arbitrary
, such that for an arbitrary , there does not exist
, there does not exist 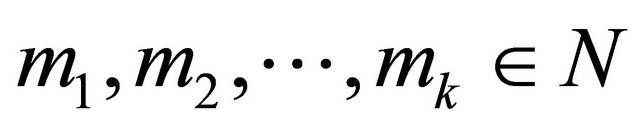 such that
such that
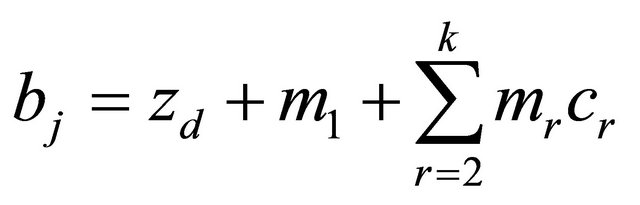 , that is, for an arbitrary
, that is, for an arbitrary
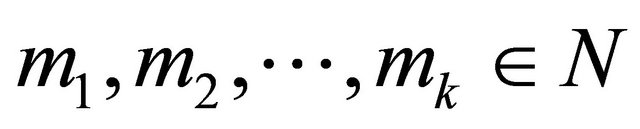 , we have
, we have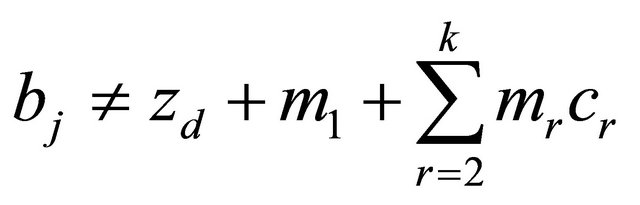 . In fact, since
. In fact, since 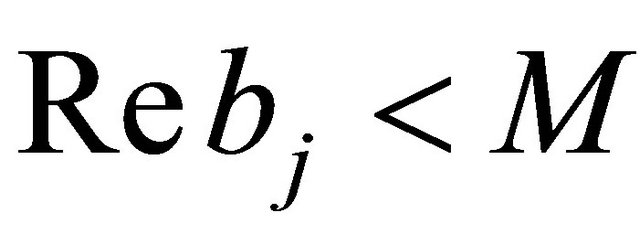 and
and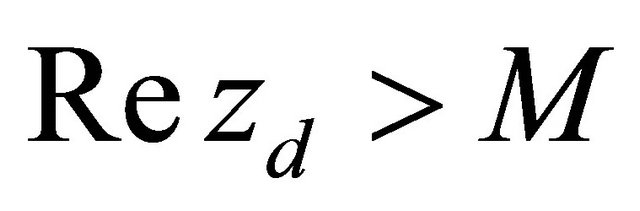 , this case appears whenever
, this case appears whenever 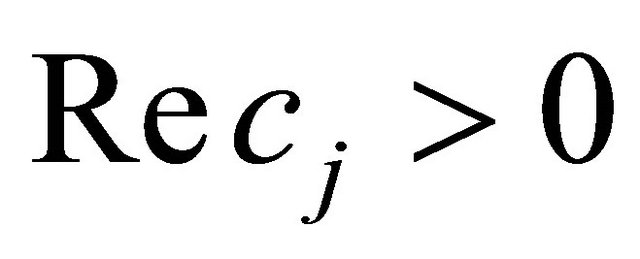 for every
for every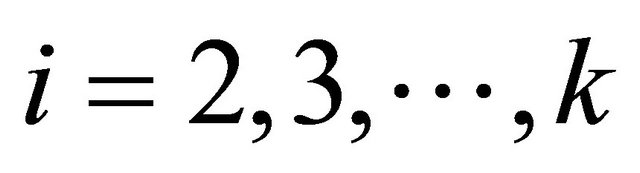 . Thereforewe know
. Thereforewe know 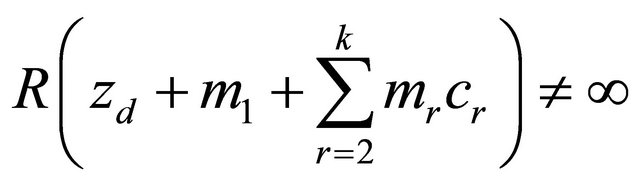 and that there exists a unbounded subsequence set
and that there exists a unbounded subsequence set  in which every
in which every
 is the poles of
is the poles of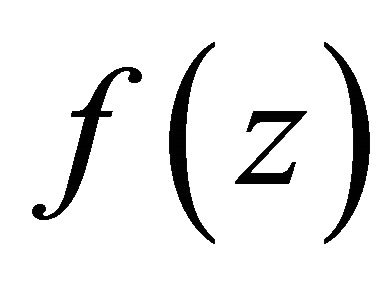 . Hence we know that there are at least one in these signs
. Hence we know that there are at least one in these signs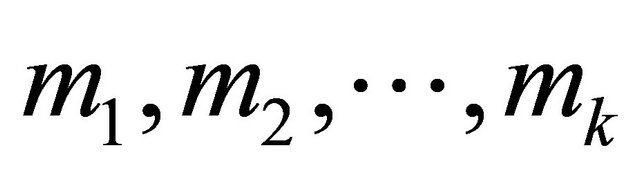 , which takes every positive integer, for instance, m1 takes every positive integer.
, which takes every positive integer, for instance, m1 takes every positive integer.
Thus, 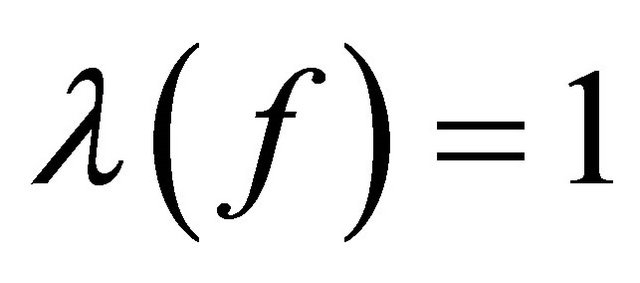 , which contradicts the hypothesis of Lemma 2.3.
, which contradicts the hypothesis of Lemma 2.3.
Case 2. There exists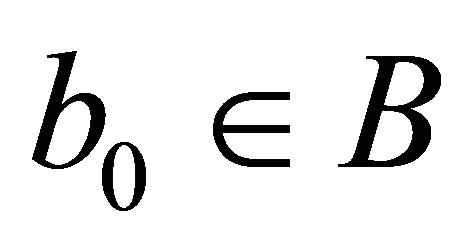 , such that for every
, such that for every , there exists
, there exists , such that
, such that
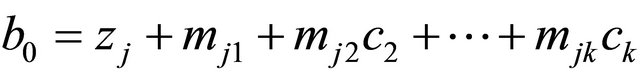 . From
. From  and
and
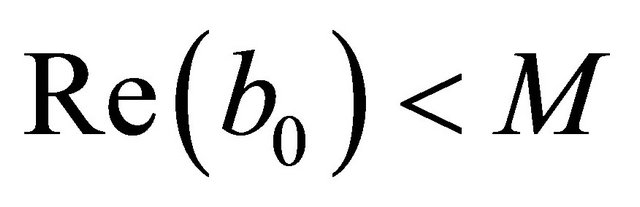 , we have that
, we have that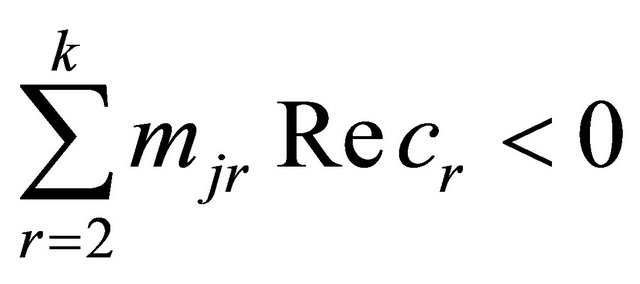 . As the set A is infinite and B has only a finite elementary, there exists
. As the set A is infinite and B has only a finite elementary, there exists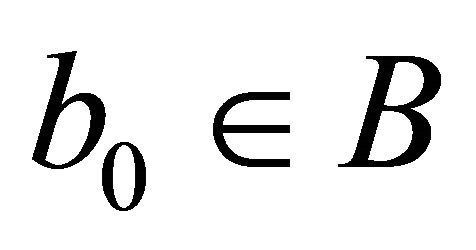 , satisfying
, satisfying
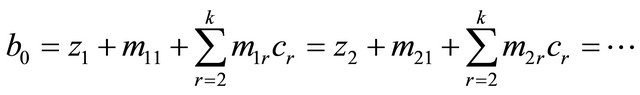 (2.5)
(2.5)
By putting 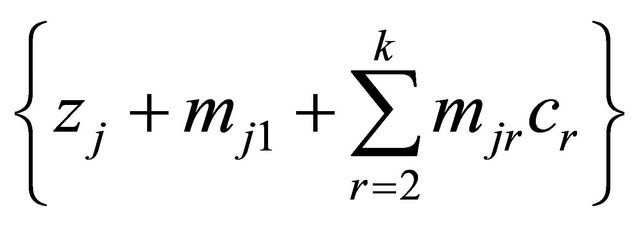 in order again, we have the following express
in order again, we have the following express
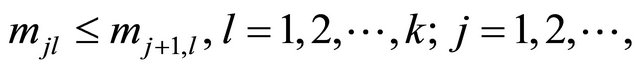
and

where
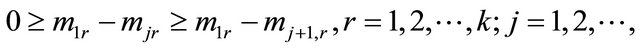 .
.
Now set
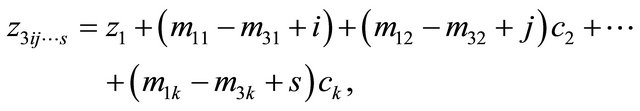
where
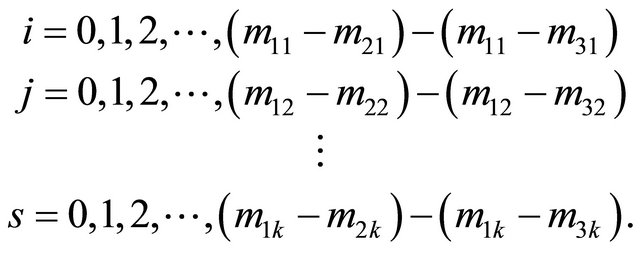
Since 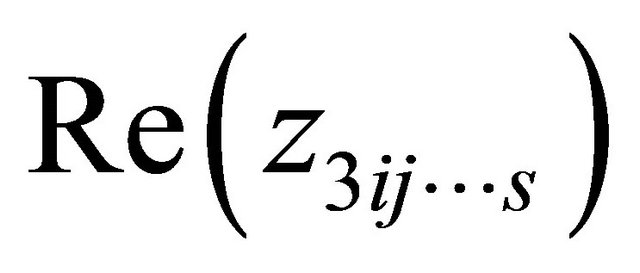 are between
are between 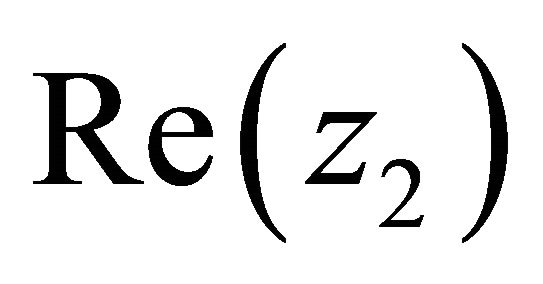 and
and ,
, 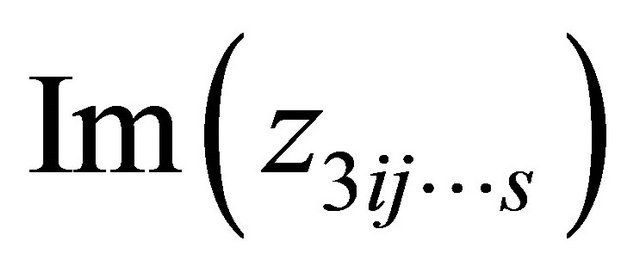 are between
are between 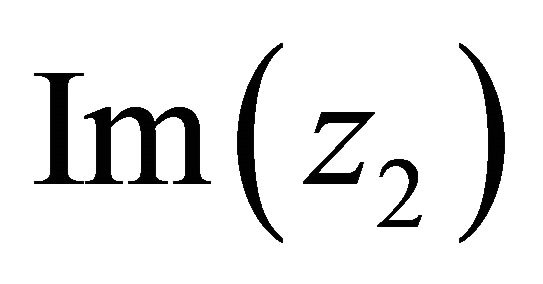 and
and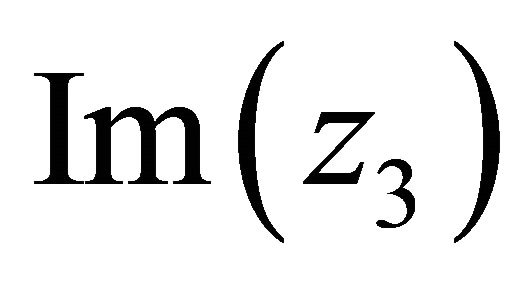 , we know that
, we know that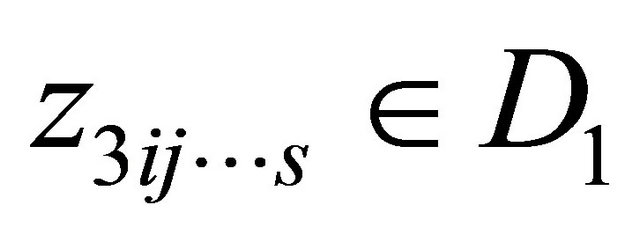 , that is,
, that is,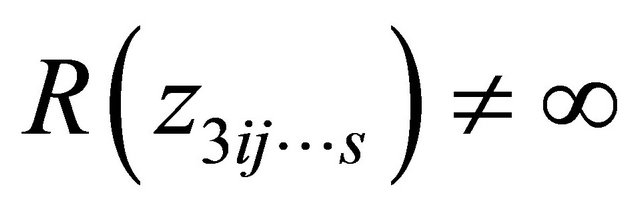 . From
. From
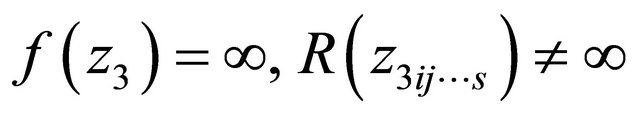 , and (2.4), we know that one of
, and (2.4), we know that one of 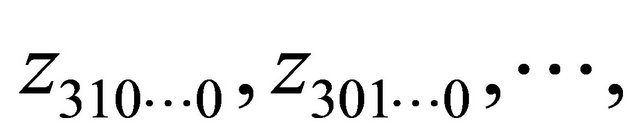 and
and 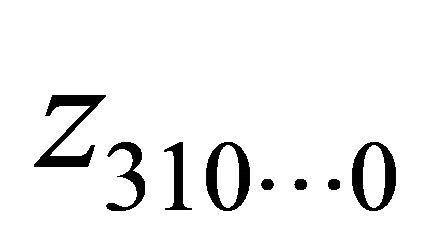 is the pole of
is the pole of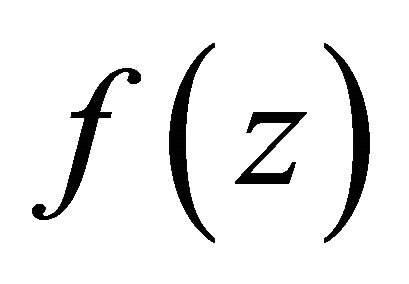 . If
. If 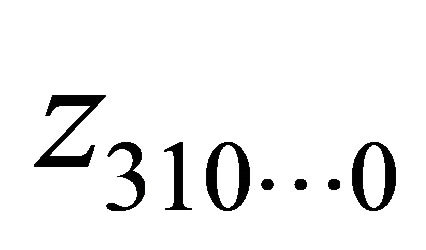 is the pole of
is the pole of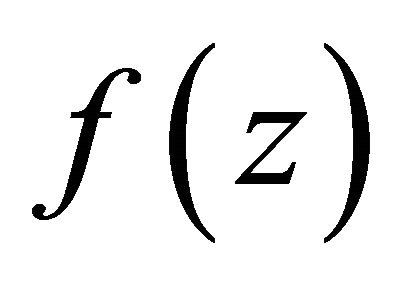 , then from the some argument above we have one of
, then from the some argument above we have one of 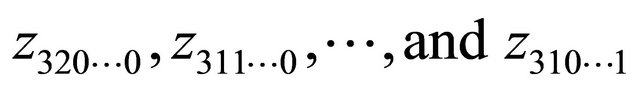 is also the pole of
is also the pole of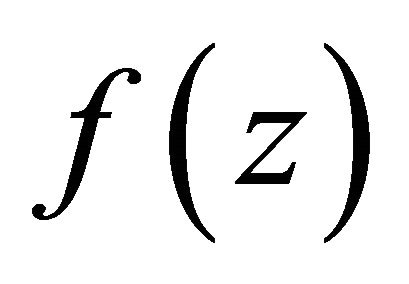 . If
. If 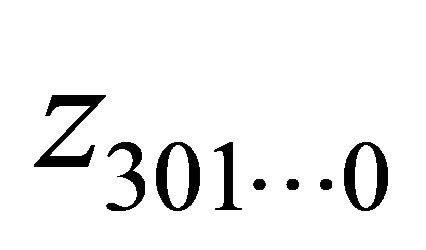 is the pole of
is the pole of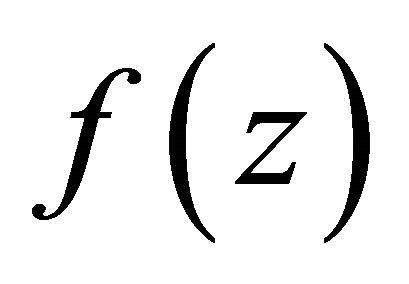 , then one of
, then one of 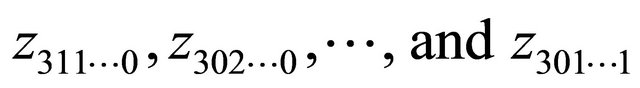 is also the pole of
is also the pole of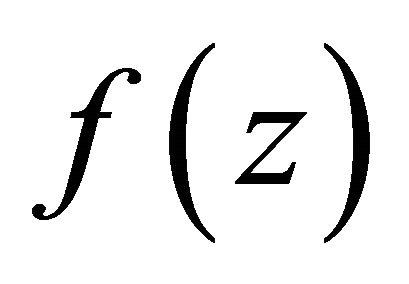 . On the analogy of this, it is not difficult to find there exists at least one of
. On the analogy of this, it is not difficult to find there exists at least one of , for instance, we assume that is j, such that j takes all value of
, for instance, we assume that is j, such that j takes all value of 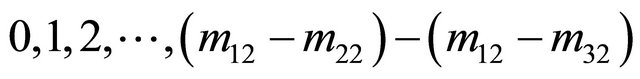 . From
. From  to
to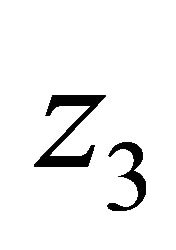 ,
, 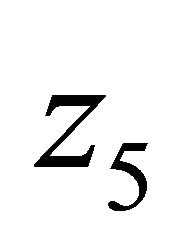 to
to , and
, and 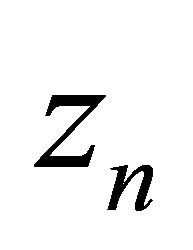 to
to , repeating above proceeding, we have
, repeating above proceeding, we have
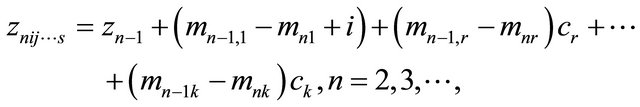
where
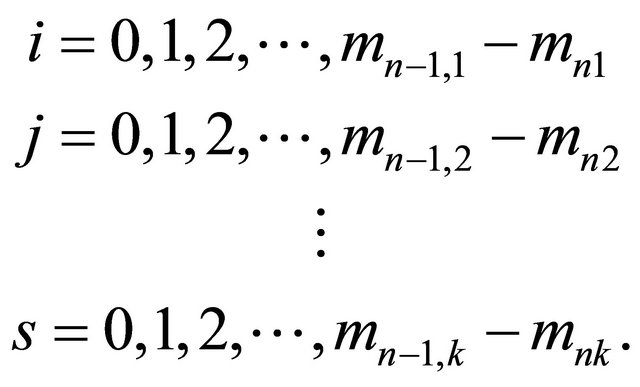
Therefore, we can see that there exist infinite many poles of 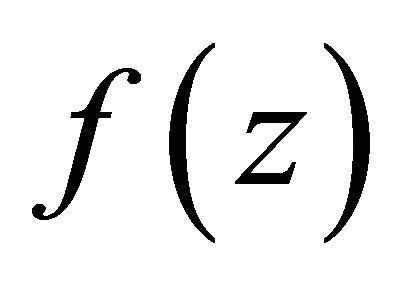 whose expressions are as follows
whose expressions are as follows
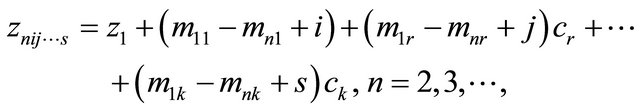
where
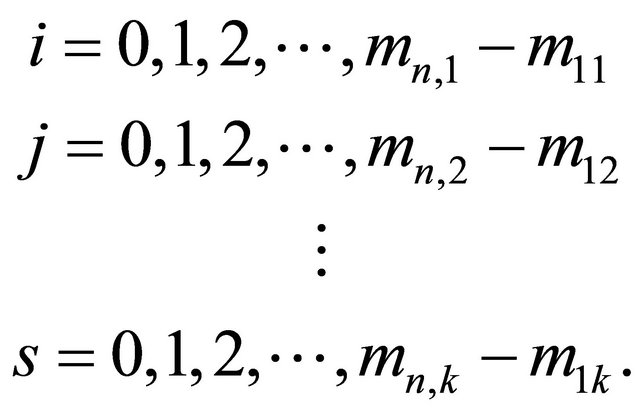
in which we can find that one of  takes every positive integer. Thus,
takes every positive integer. Thus, 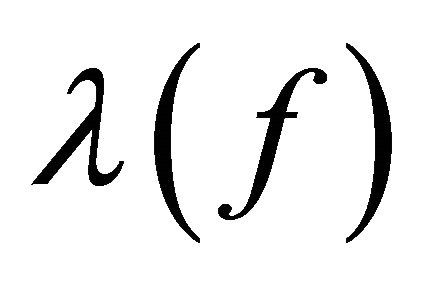 , which still contradict the hypothesis on the growth order of
, which still contradict the hypothesis on the growth order of 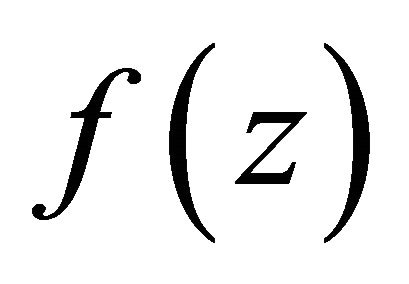 in Lemma 2.3.
in Lemma 2.3.
By the similar method to above, it is easy to prove that 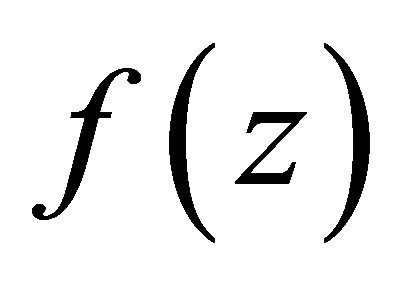 has at most finite many poles whenever quotient of difference polynomials
has at most finite many poles whenever quotient of difference polynomials
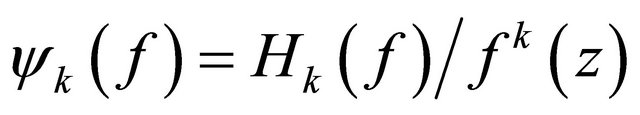
is rational functions. 
Lemma 2.4. Let 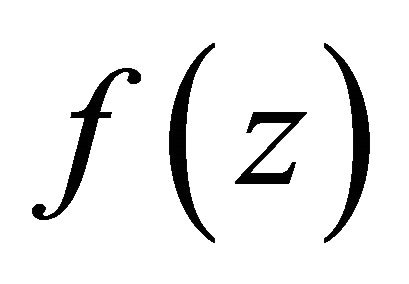 be a function transcendental and meromorphic in the plane with growth order
be a function transcendental and meromorphic in the plane with growth order
 . Supposed that
. Supposed that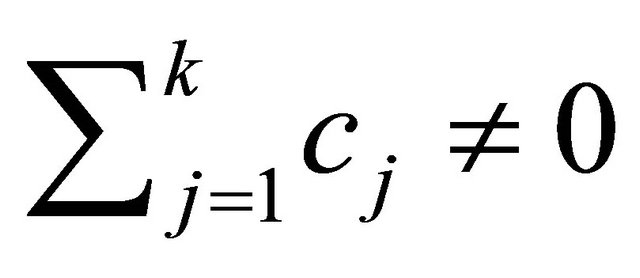 , then the homogeneous difference polynomials
, then the homogeneous difference polynomials
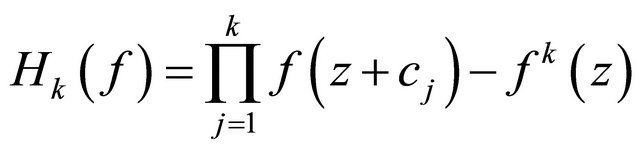
and
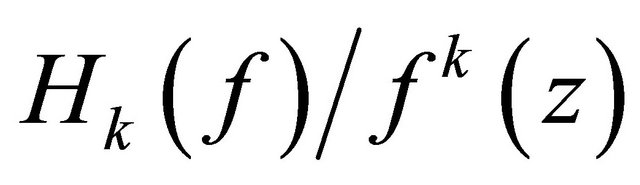
also are transcendental.
Proof. Suppose first that there exists a rational function , such that
, such that
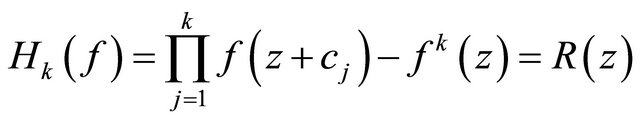 (2.6)
(2.6)
By Lemma 2.3, 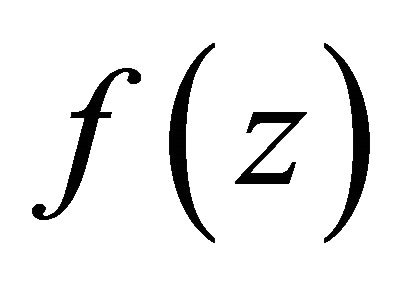 has at most finite many poles. Again from Lemma 2.1, there exists
has at most finite many poles. Again from Lemma 2.1, there exists 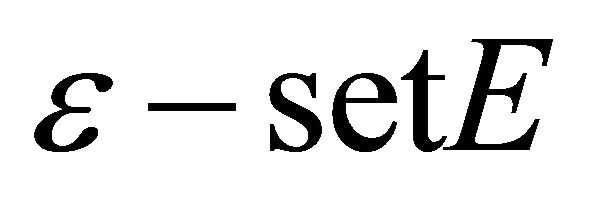 such that as
such that as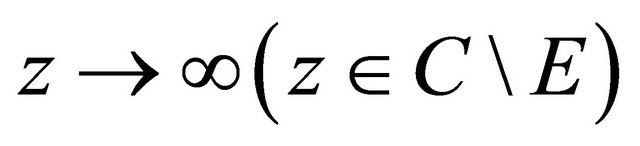 , we have
, we have
 (2.7)
(2.7)
It follows that from (2.6) and (2.7)
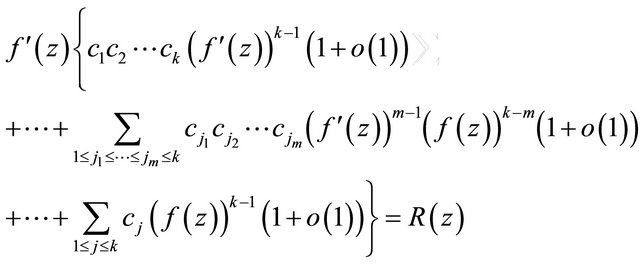 (2.8)
(2.8)
We write 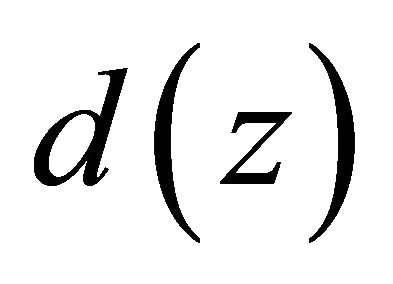 for a polynomial formed by the pole of
for a polynomial formed by the pole of , and
, and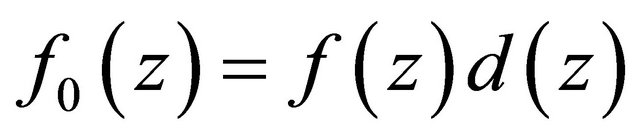 . So
. So 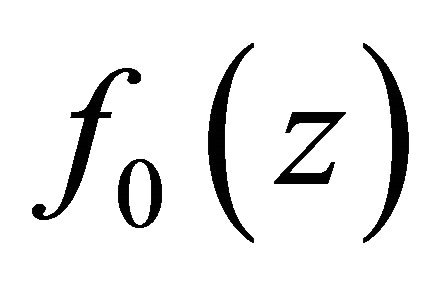 is an entire function, and
is an entire function, and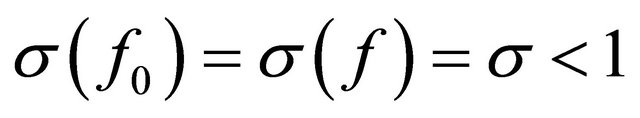 . With the standard result in the Wiman-Valiron Theory, we know that there exists a subset
. With the standard result in the Wiman-Valiron Theory, we know that there exists a subset  with finite logarithmic measure
with finite logarithmic measure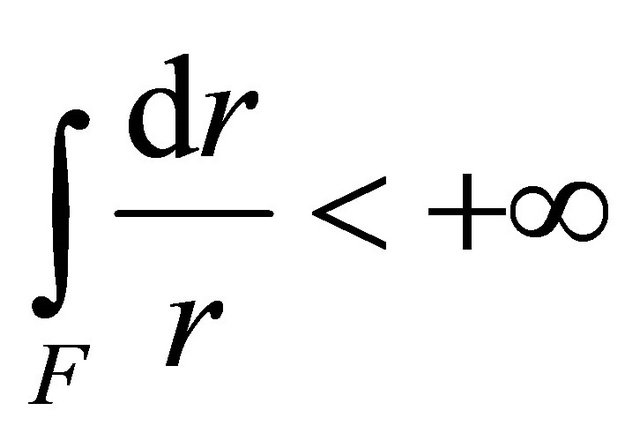 , in which for an sufficiently large
, in which for an sufficiently large
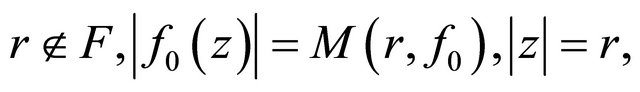 the following equality holds
the following equality holds
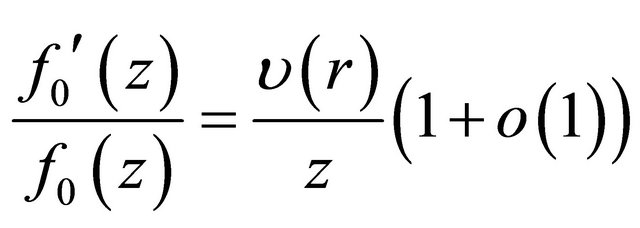 .
.
Thus,
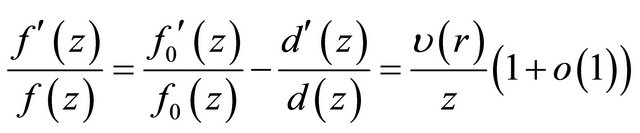 (2.9)
(2.9)
where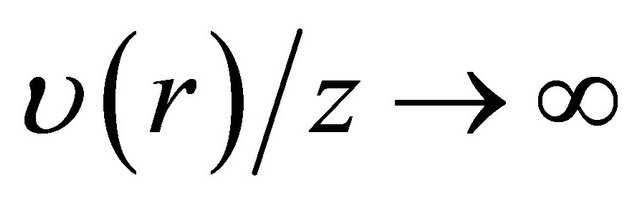 , and
, and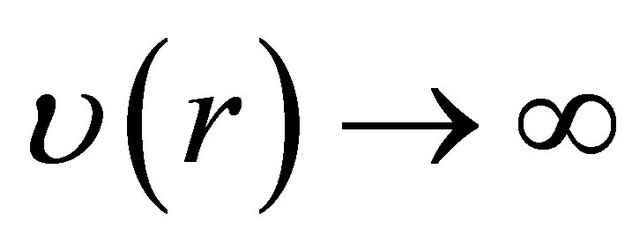 , as
, as![]() . Set
. Set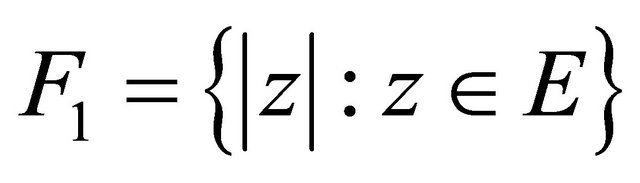 . Since
. Since  is
is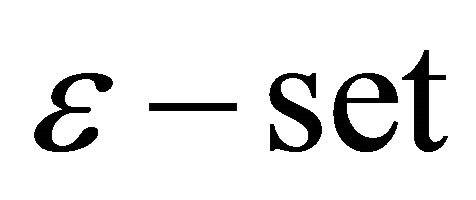 , we have that F1 also is of finite logarithmic measure. Therefore, for all z,
, we have that F1 also is of finite logarithmic measure. Therefore, for all z,  , and
, and
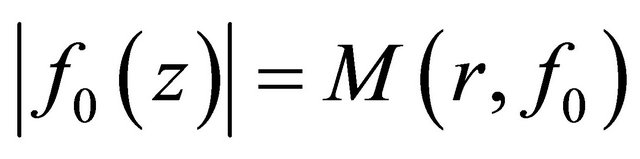 we immediately deduce that from (2.8) and (2.9)
we immediately deduce that from (2.8) and (2.9)
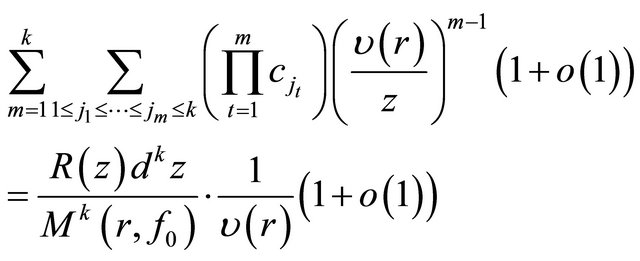 (2.10)
(2.10)
Since 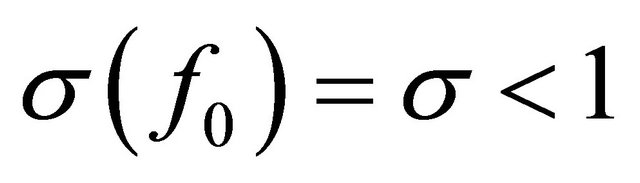 and
and  is transcendental, there exists a sequence
is transcendental, there exists a sequence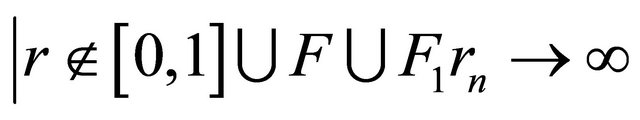 , such that for arbitrary
, such that for arbitrary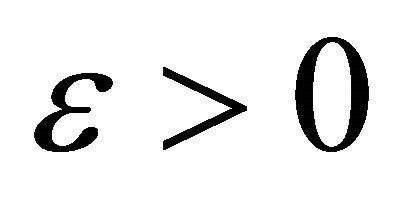 , we have that
, we have that
![]() (2.11)
(2.11)
 . (2.12)
. (2.12)
Then, we induce that from (2.4) and (2.11)
 . (2.13)
. (2.13)
Therefore, from (2.12) and (2.13) we have
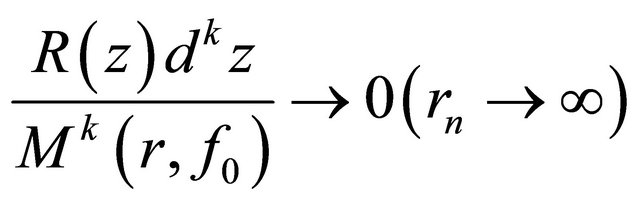 (2.14)
(2.14)
By (2.10), (2.12), and (2.14), we deduce easily that , which contradicts the assumption on
, which contradicts the assumption on , that is,
, that is, 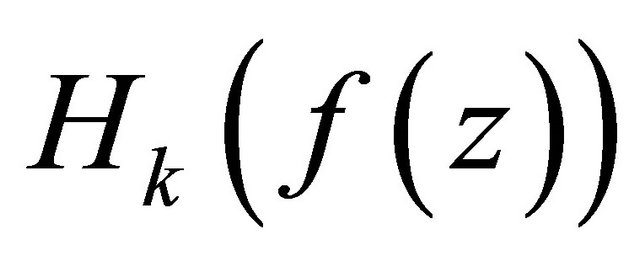 transcendental.
transcendental.
Lemma 2.5. Let 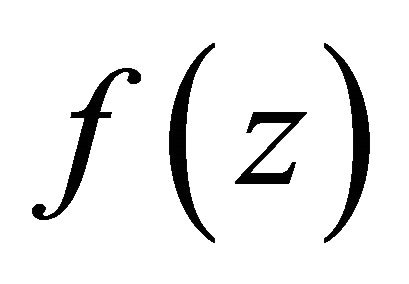 be a function transcendental and meromorphic in the plane, whose growth orde
be a function transcendental and meromorphic in the plane, whose growth orde 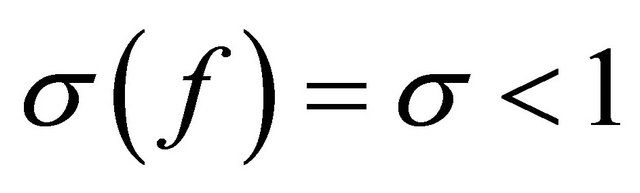 . Supposed that
. Supposed that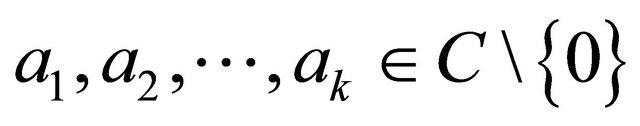 , and
, and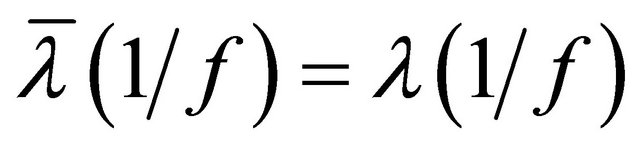 . Then
. Then
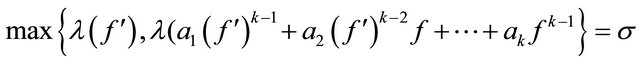
Proof. For 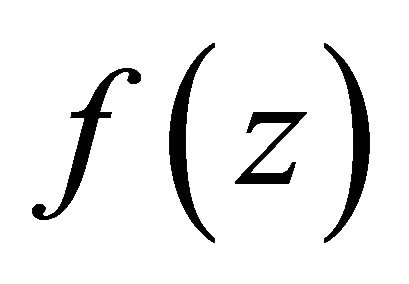 of growth order
of growth order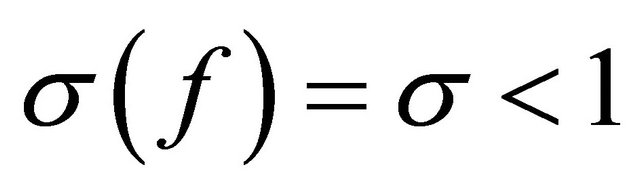 , from Hadamard’s factorization theorem we have
, from Hadamard’s factorization theorem we have
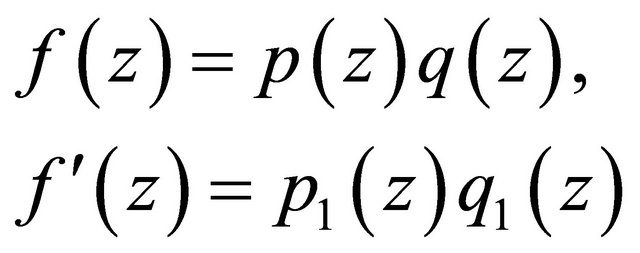 , (2.15)
, (2.15)
where 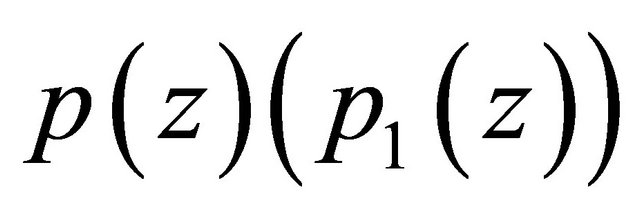 and
and  are respectively the canonical product of zeros and poles of
are respectively the canonical product of zeros and poles of 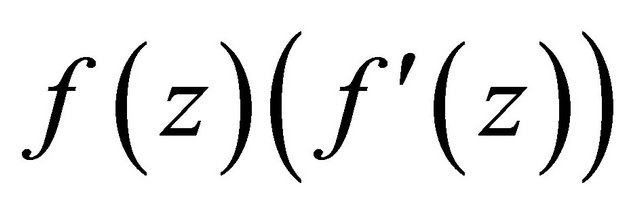 , satisfying
, satisfying
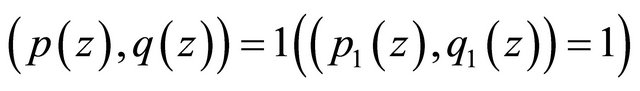 .
.
From (2.15), we have
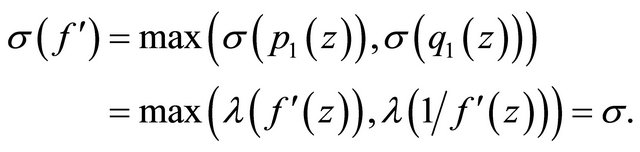
Therefore, if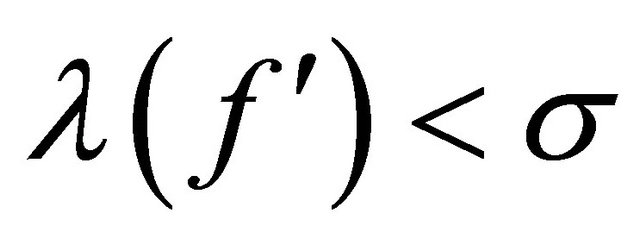 , we deduce that
, we deduce that 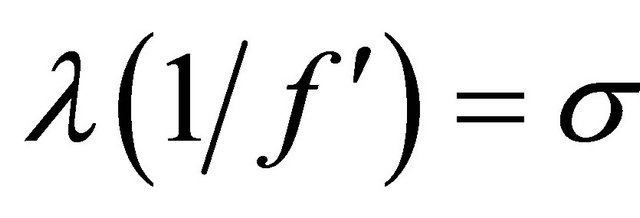 . For
. For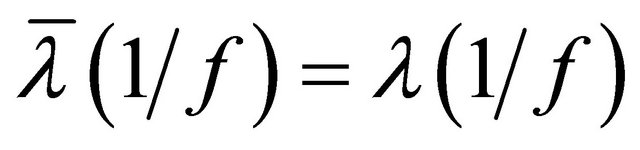 , the following equations hold
, the following equations hold
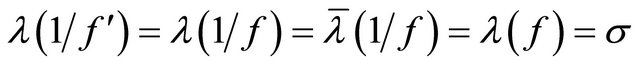 (2.16)
(2.16)
We have that from 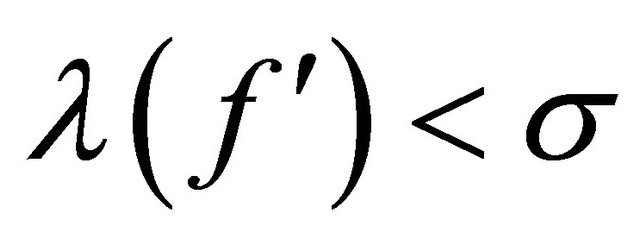 and (2.16)
and (2.16)
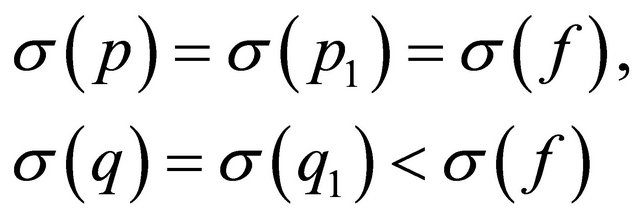 . (2.17)
. (2.17)
If 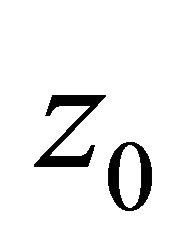 is a poles of
is a poles of 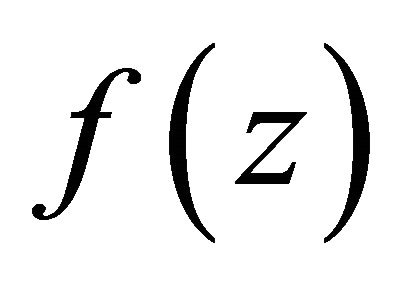 with multiplicity m, then
with multiplicity m, then 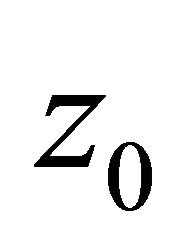 must be a poles of
must be a poles of 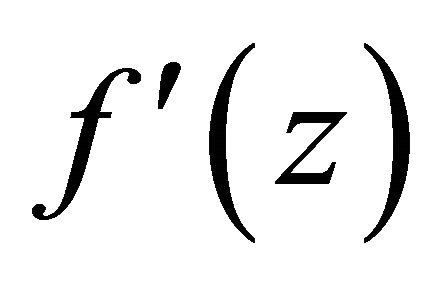 with multiplicity
with multiplicity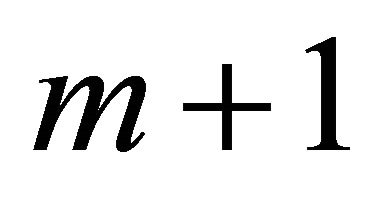 , so that we denote
, so that we denote 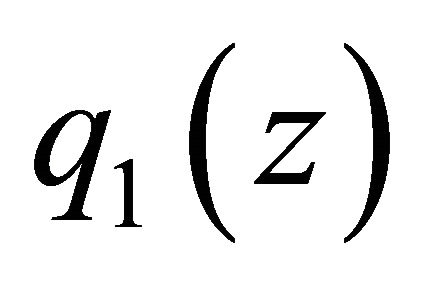 by
by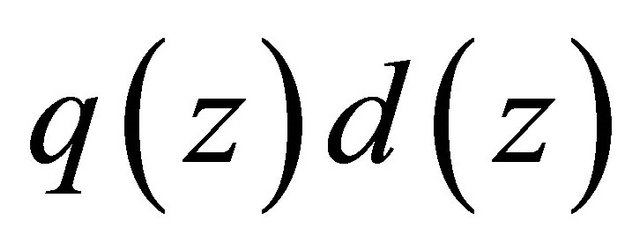 , that is,
, that is,
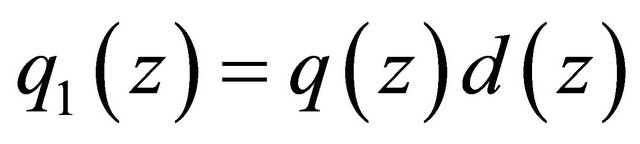 , (2.18)
, (2.18)
where 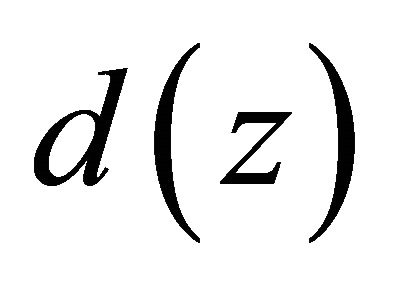 is a canonical product of distinct poles of
is a canonical product of distinct poles of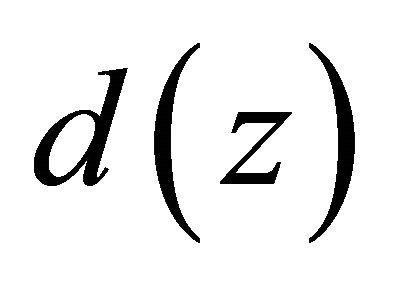 . By (2.16), we obtain that
. By (2.16), we obtain that
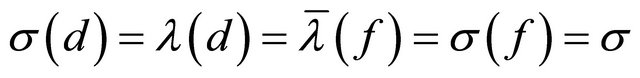 . (2.19)
. (2.19)
From (2.15) and (2.18), we deduce that
 (2.20)
(2.20)
Thus, if z0 is the pole of 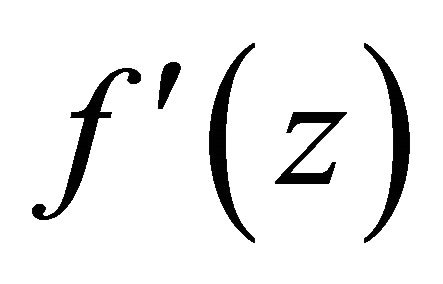 (that is,
(that is,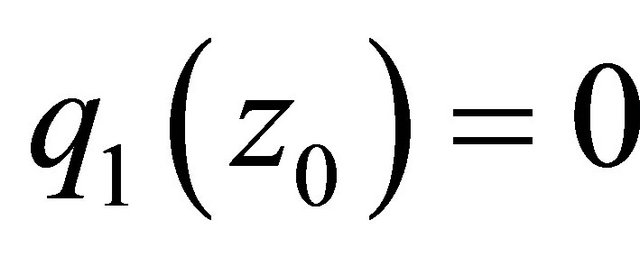 ), then
), then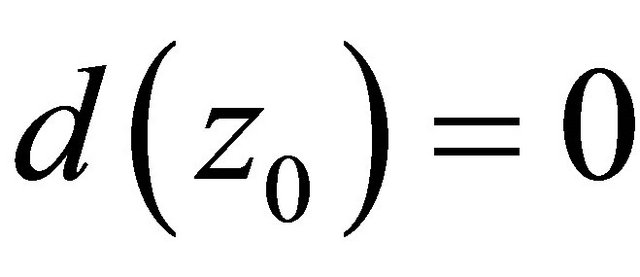 ,
, 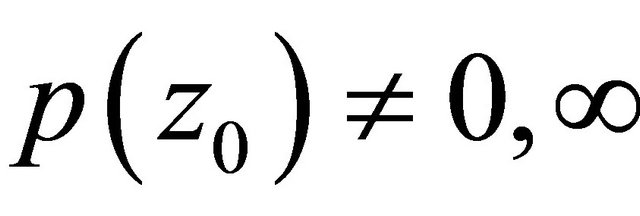 , but
, but . Hence, we have that
. Hence, we have that 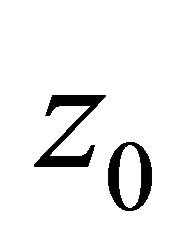 is not the zero of
is not the zero of
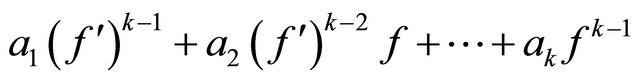 .
.
So that
 and
and
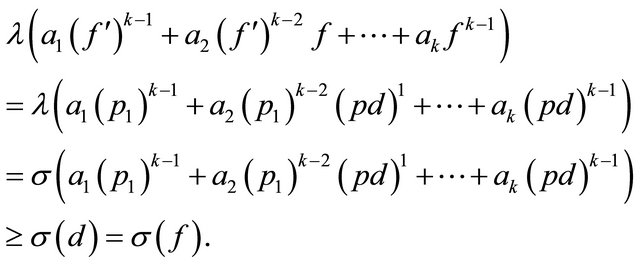
This completes the proof of Lemma 2.5. 
3. Proofs of Theorem 1.5
From Lemma 2.2 we see that there exists a sufficiently large , a positive number
, a positive number 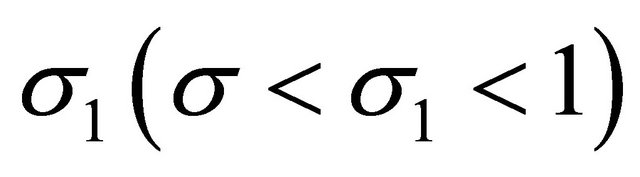 such that
such that
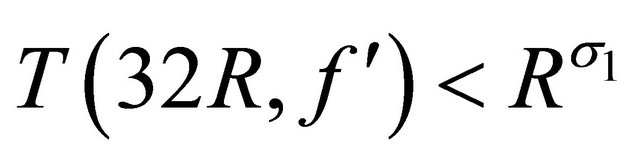 (2.21)
(2.21)
and there exists a set 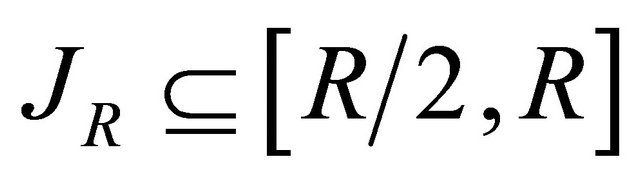 with linear measure
with linear measure , such that for any
, such that for any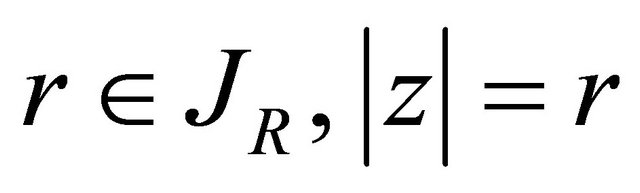 , we have the following equation
, we have the following equation
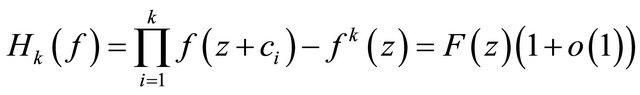 , (2.22)
, (2.22)
where 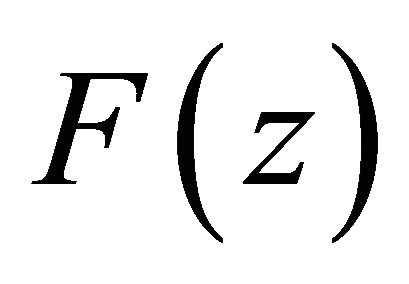 satisfies the following express,
satisfies the following express,
 , (2.23)
, (2.23)
here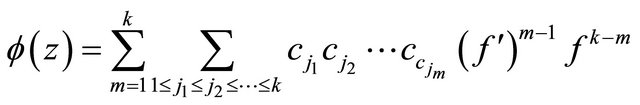 .
.
On the other hand, under the condition of Theorem 1.5 and from Lemma 2.4 we know 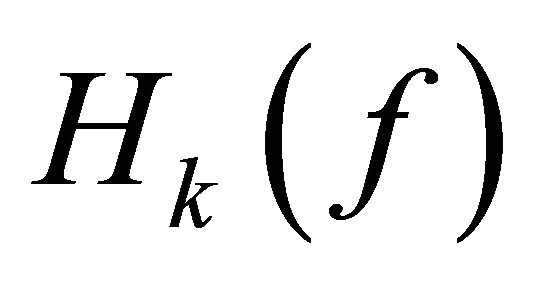 transcendental.
transcendental.
Suppose that 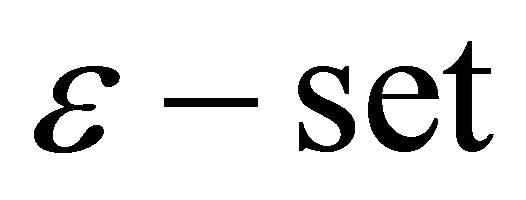 E concludes all of zeros and poles of
E concludes all of zeros and poles of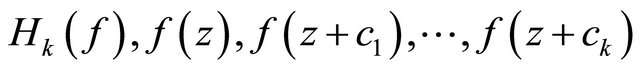 , and
, and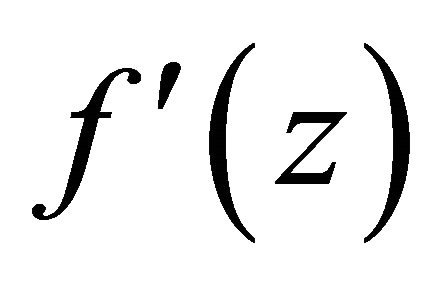 . Setting
. Setting
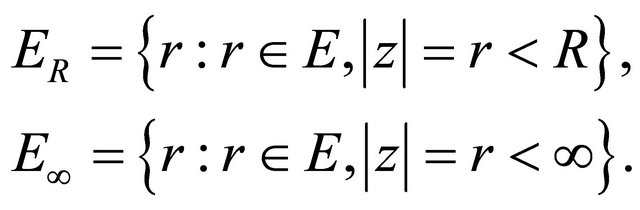
Since the property of 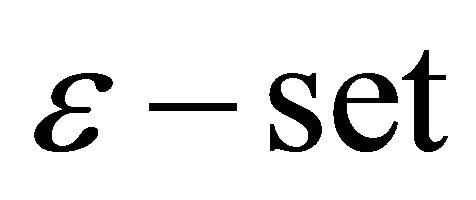 and
and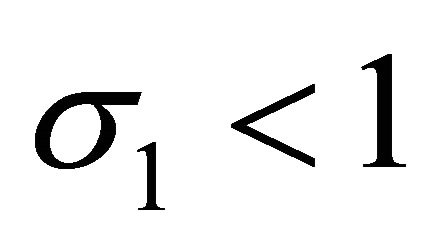 , we have that
, we have that 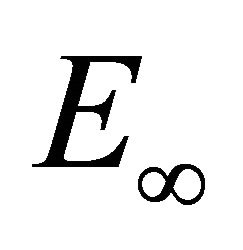 is with finite logarithmic measure, and
is with finite logarithmic measure, and 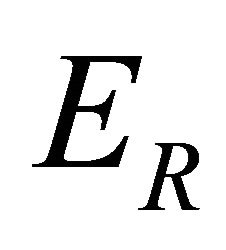 has linear measure
has linear measure 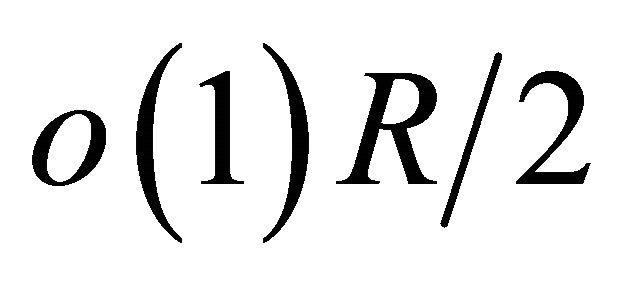 for sufficiently large
for sufficiently large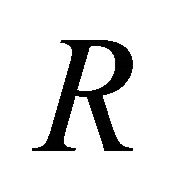 .
.
We assume that  is a set, such that
is a set, such that
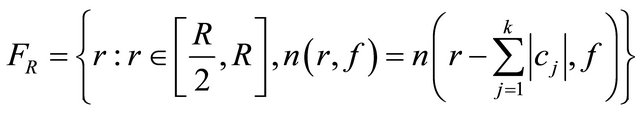 . (2.24)
. (2.24)
Noting that there exists 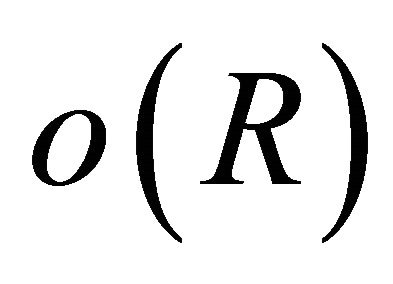 many points
many points
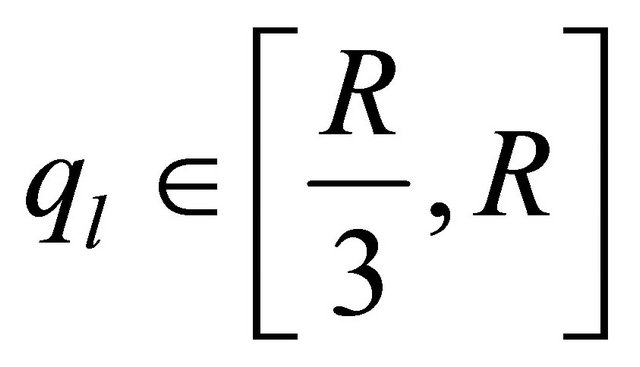 at most from (2.22), at which
at most from (2.22), at which 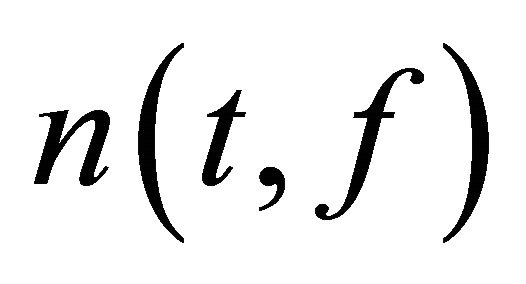 is not continuous, and also for any
is not continuous, and also for any 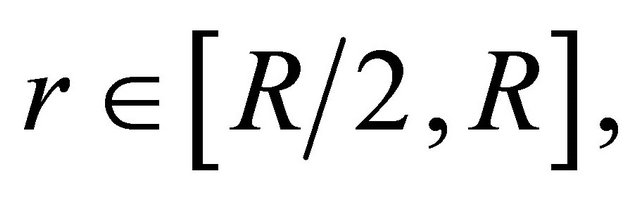
 holds for some
holds for some  whenever
whenever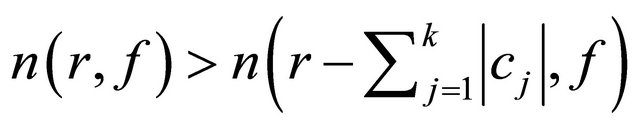 . Therefore,
. Therefore, 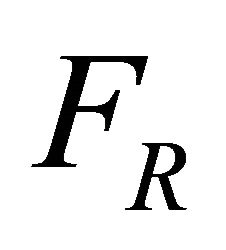 has linear measure
has linear measure
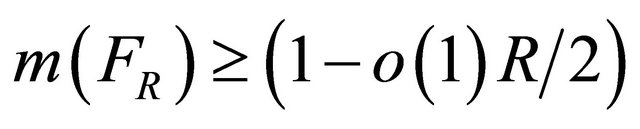 , (2.25)
, (2.25)
From (2.23)-(2.25), we know that there exists 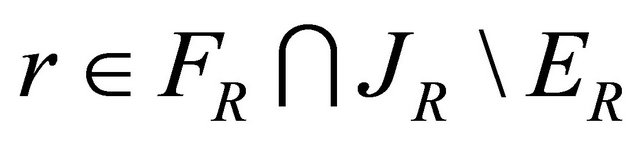 such that
such that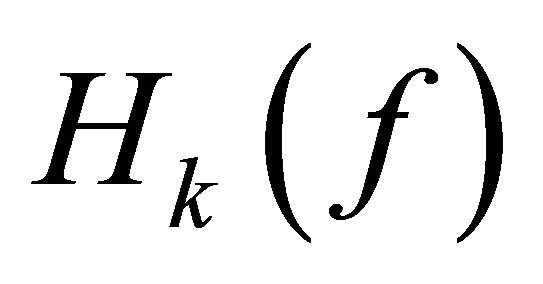 ,
, 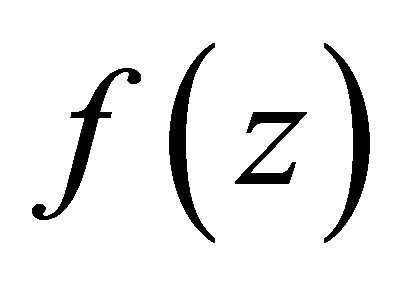 ,
,  ,
, 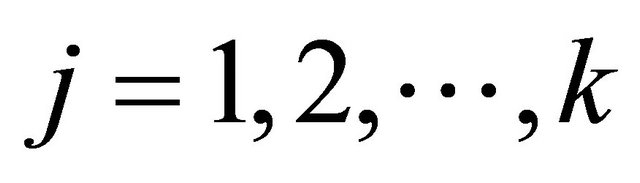 , and
, and 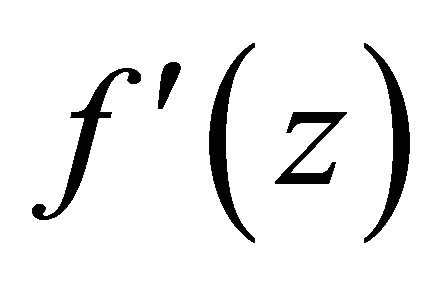 have no zeros and poles on the circle
have no zeros and poles on the circle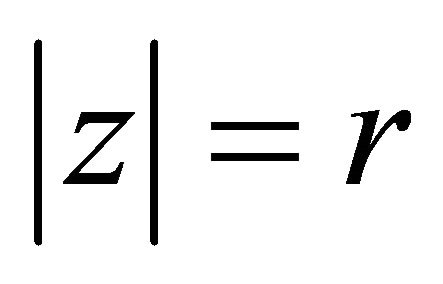 . Therefore,
. Therefore,
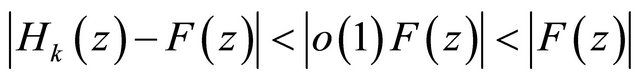 . (2.26)
. (2.26)
Applying Rouché’s Theorem to 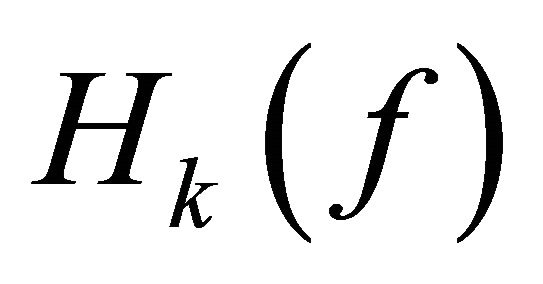 and
and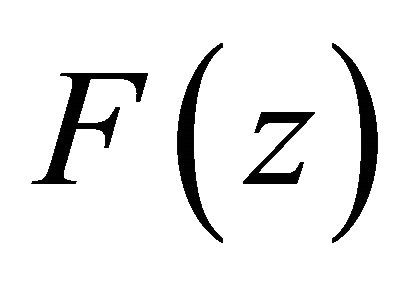 , we obtain the following equation
, we obtain the following equation
 . (2.27)
. (2.27)
Without loss of generality, we may assume that
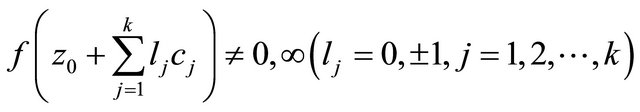
for all poles 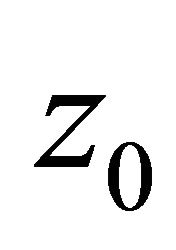 of
of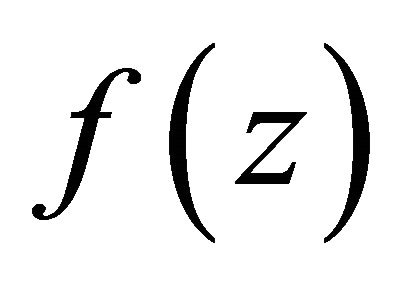 . From the assumption in Theorem 1.3, we know that there exists positive number
. From the assumption in Theorem 1.3, we know that there exists positive number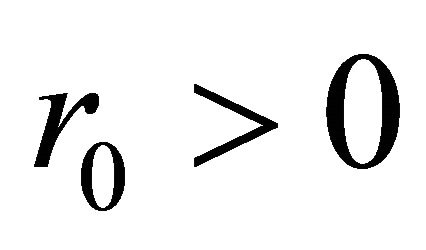 , which does not depend on R and r, such that if
, which does not depend on R and r, such that if 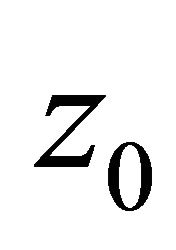 is a pole of
is a pole of 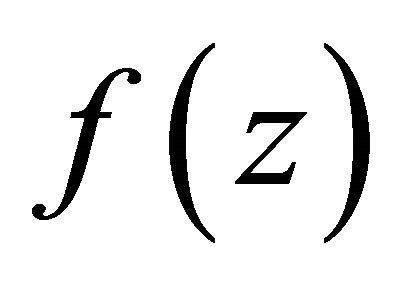 with multiplicity
with multiplicity![]() ,
,
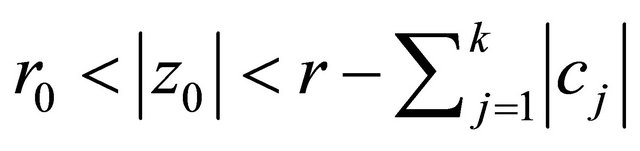 then by the expression of
then by the expression of 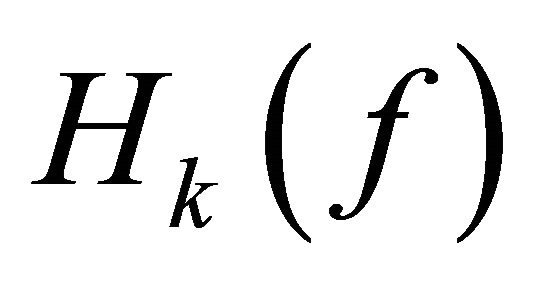 and
and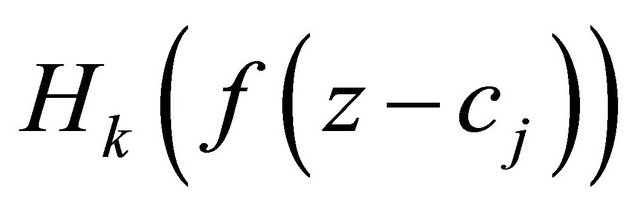 ,
,
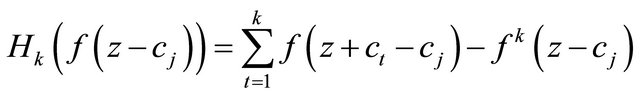
we see that z0, 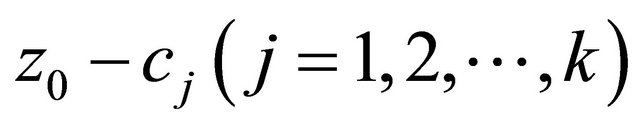 are respectively the pole of
are respectively the pole of 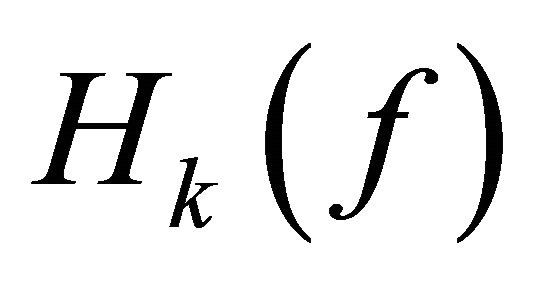 with multiplicity
with multiplicity . Therefore, we deduce that
. Therefore, we deduce that
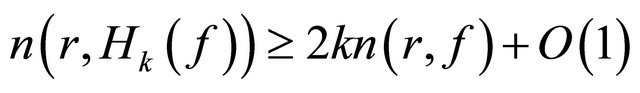 . (2.28)
. (2.28)
Since the pole z0 of 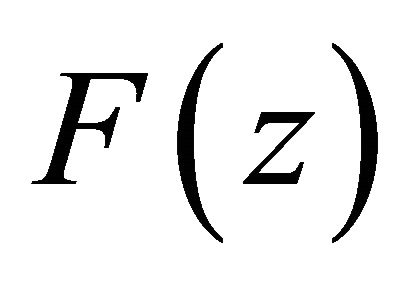 has multiplicity
has multiplicity , we have the following equality
, we have the following equality
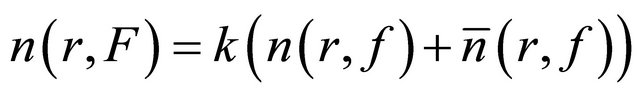 . (2.29)
. (2.29)
And obviously,
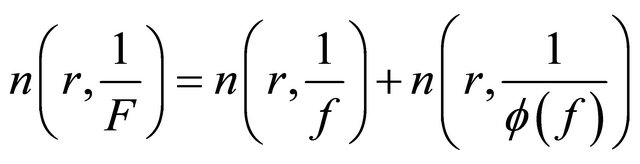 . (2.30)
. (2.30)
Substituting (2.28), (2.30) into (2.27), we obtain
 (2.31)
(2.31)
If , then
, then . Thus, we have that by (2.31)
. Thus, we have that by (2.31)
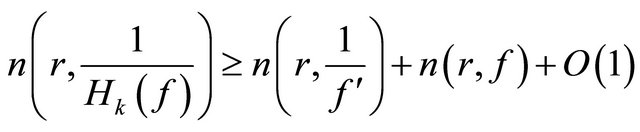 , (2.32)
, (2.32)
then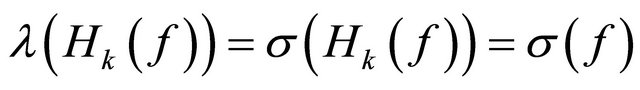 .
.
If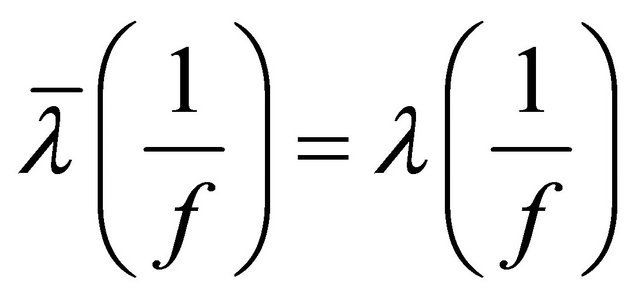 , we have that from (2.31)
, we have that from (2.31)
 . (2.33)
. (2.33)
By Lemma 2.5 and (2.33), we deduce that
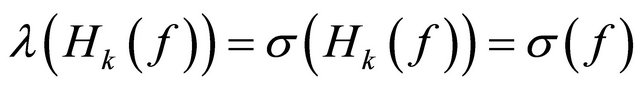 .
.
In particular, if 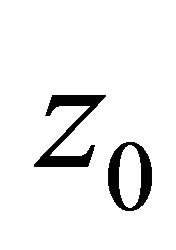 is the zero of
is the zero of
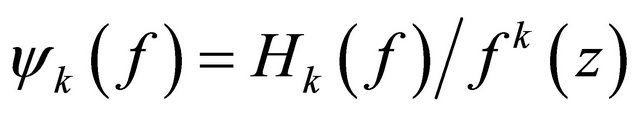 then z0 is, also the zero of
then z0 is, also the zero of . On the other hand, if z1 is the zero of
. On the other hand, if z1 is the zero of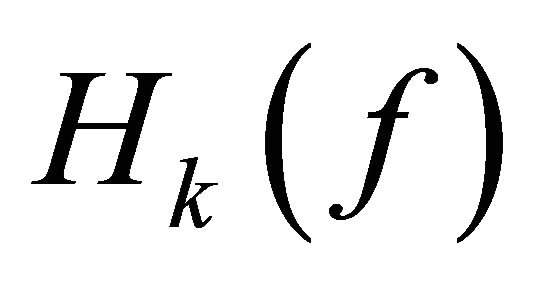 , but not the zero of
, but not the zero of , then z1 must be the zero of
, then z1 must be the zero of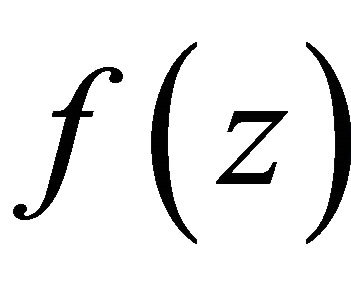 , that is,
, that is,  for some j. From the assumption in Theorem 1.5 that
for some j. From the assumption in Theorem 1.5 that 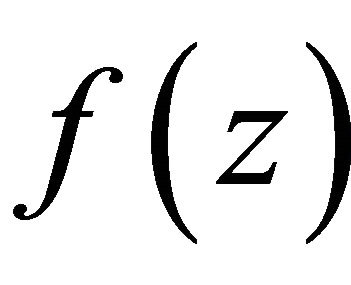 has at most finitely many zeros
has at most finitely many zeros 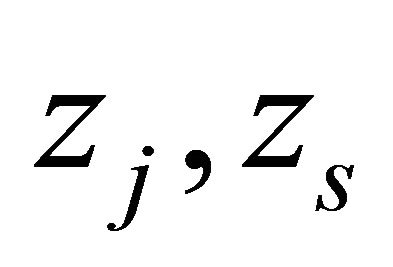 satisfying
satisfying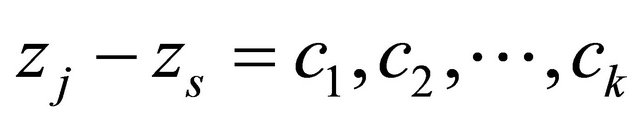 , we have
, we have
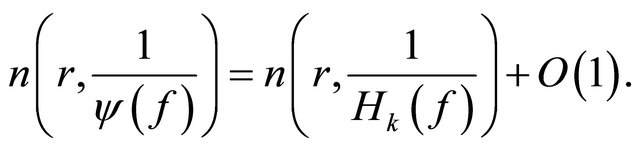
Therefore,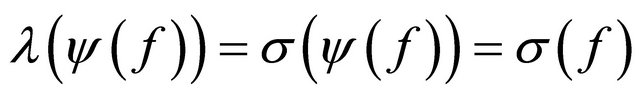 .
.
REFERENCES
- J. M. Whittaker, “Interpolatory Function Theory,” Cambridge Tracts in Mathematics and Mathematical Physics, No. 33, Cambridge University Press, New York, 1935, p. 52.
- M. Ablowitz, R. G. Halburd and B. Herbst, “On the Extension of Painleve Property to Difference Equations,” Nonlinearty, Vol. 13, No. 3, 2000, pp. 889-905. doi:10.1088/0951-7715/13/3/321
- R. G. Halburd and R. Korhonen, “Difference Analogue of the Lemma on the Logarithmic Derivative with Applications to Difference Equations,” Journal of Mathematical Analysis and Applications, Vol. 314, No. 2, 2006, pp. 477- 487. doi:10.1016/j.jmaa.2005.04.010
- R. G. Halburd and R. Korhonen, “Nevanlinna Theory for the Difference Operator,” Annales Academiae Scientiarum Fennicae Mathematica, Vol. 31, No. 2, 2006, pp. 463- 478.
- I. Laine and C. C. Yang, “Value Distribution of Difference Polynomials,” Proceedings of the Japan Academy, Vol. 83, No. 8, 2007, pp. 148-151. doi:10.3792/pjaa.83.148
- Y. M. Chiang and S. J. Feng, “On the Nevanlinna Characteristic of f(z + c) and Difference Equations in the Complex Plane,” The Ramanujan Journal, Vol. 16, No. 1, 2008, pp. 105-129. doi:10.1007/s11139-007-9101-1
- W. Bergweiler and J. K. Langley, “Zeros of Differences of Meromorphic Functions,” Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 142, No. 1, 2007, pp. 133-147. doi:10.1017/S0305004106009777
- Z. X. Chen and K. H. Shon, “On Zeros and Fixed Points of Difference of Meromorphic Functions,” Journal of Mathematical Analysis and Applications, Vol. 344, No. 1, 2008, pp. 373-383. doi:10.1016/j.jmaa.2008.02.048
- Z. X. Chen and K. H. Shon, “Estimates for the Zeros of Difference of Meromorphic Functions,” Science China, Series A, Vol. 52, No. 11, 2009, pp. 2447-2458. doi:10.1007/s11425-009-0159-7
NOTES
*Supported by China Industrial Technology Development Program (B3120110001) and Sichuan Provincial Science and Technology Department of Applied Foundation Project (07JY029-006).

