Advances in Pure Mathematics
Vol.2 No.6(2012), Article ID:24670,5 pages DOI:10.4236/apm.2012.26064
On Humbert Matrix Polynomials of Two Variables
1Department of Mathematics, Al-Aqsa University, Gaza Strip, Palestine
2Department of Mathematics, Faculty of Science, Assiut University, Assiut, Egypt
Email: ghazikhamash@yahoo.com, drshehata2006@yahoo.com
Received July 13, 2012; revised September 6, 2012; accepted September 14, 2012
Keywords: Humbert Matrix Polynomials of Two Variables; Hypergeometric Matrix Function; Matrix Functional Calculus
ABSTRACT
In this paper we introduce Humbert matrix polynomials of two variables. Some hypergeometric matrix representations of the Humbert matrix polynomials of two variables, the double generating matrix functions and expansions of the Humbert matrix polynomials of two variables in series of Hermite polynomials are given. Results of Gegenbauer matrix polynomials of two variables follow as particular cases of Humbert matrix polynomials of two variables.
1. Introduction
The special matrix functions appear in statistics, lie group theory and number theory [1-4] and the matrix polynomials have become more important and some results in the theory of classical orthogonal polynomials have been extended to orthogonal matrix polynomials see for instance [5-9].
If 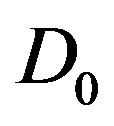 is the complex plane cut along the negative, real axis and log
is the complex plane cut along the negative, real axis and log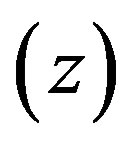 denotes the principal logarithm of z (Saks, S. and A. Zygmund, [10]), then
denotes the principal logarithm of z (Saks, S. and A. Zygmund, [10]), then 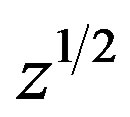 represents
represents 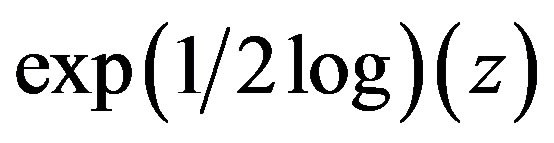 if A is a matrix in
if A is a matrix in 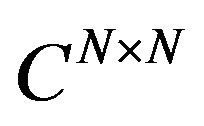 the set of all the eigenvalues of is denoted by the set of all the eigenvalues of A is denoted by
the set of all the eigenvalues of is denoted by the set of all the eigenvalues of A is denoted by . If
. If 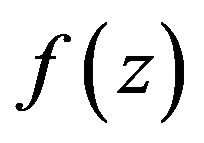 and
and  are holomorphic functions of the complex variable z, which are defined in an open set
are holomorphic functions of the complex variable z, which are defined in an open set  of the complex plane, and A is a matrix in
of the complex plane, and A is a matrix in  such that
such that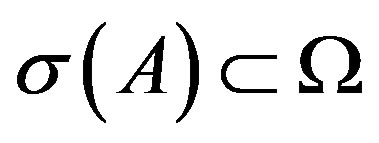 . Then from the properties of the matrix functional calculus, (Dunford N. and J. Schwartz J. [11]), it follows that
. Then from the properties of the matrix functional calculus, (Dunford N. and J. Schwartz J. [11]), it follows that . If A is a matrix with
. If A is a matrix with 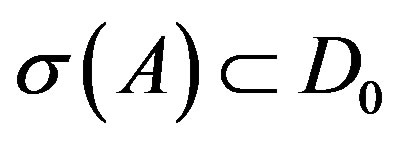 , then
, then 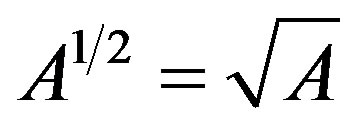 denotes the a image by
denotes the a image by 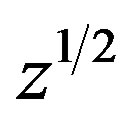 of the matrix functional calculus acting on the matrix A. we say that A is a positive stable matrix if
of the matrix functional calculus acting on the matrix A. we say that A is a positive stable matrix if 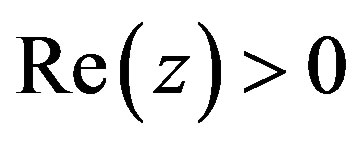 for all
for all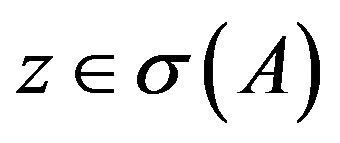 .
.
For any matrix P in 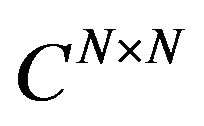 we will exploit the following relation due to [12]
we will exploit the following relation due to [12]
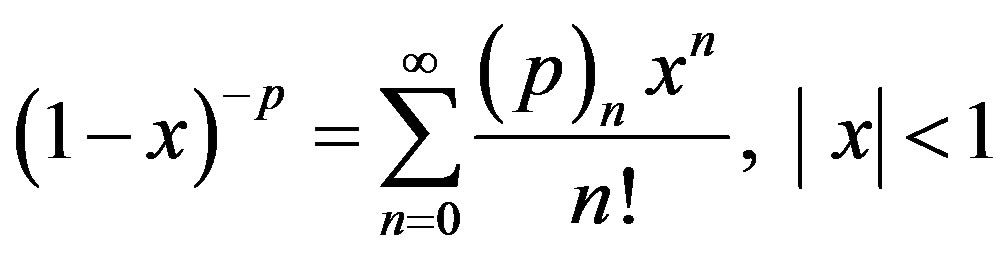 (1)
(1)
Khammash [12], define the Gegenbauer matrix polynomials of two variables by
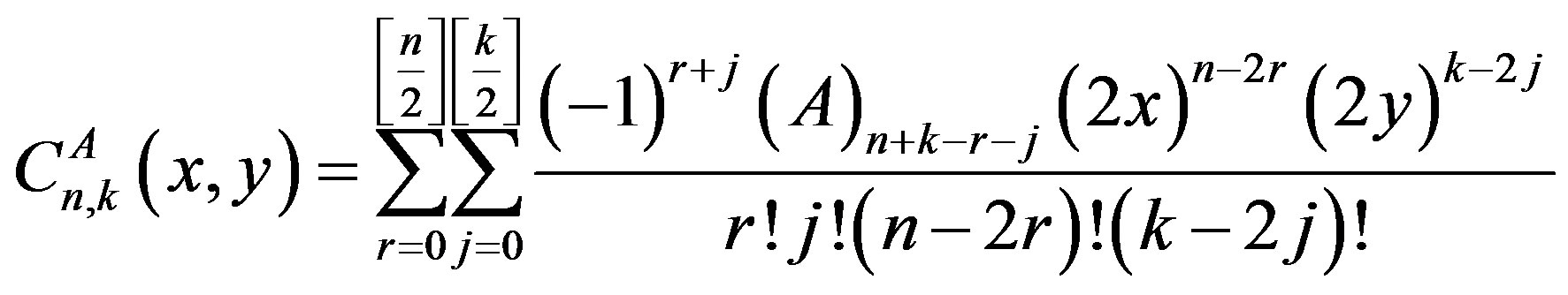 (2)
(2)
From which it follows that 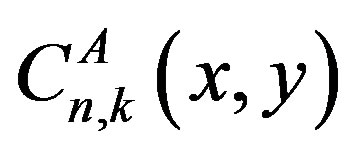 is a matrix polynomial in two variables x and y of degree precisely n in x and k in y.
is a matrix polynomial in two variables x and y of degree precisely n in x and k in y.
Also we recall that if 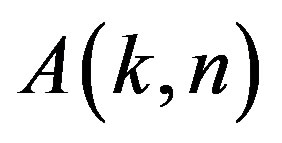 are matrix in
are matrix in 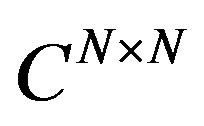 for
for 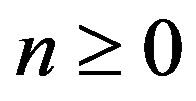 and
and 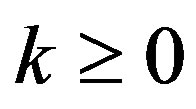 that it follows that (Defez and Jódar [14])
that it follows that (Defez and Jódar [14])
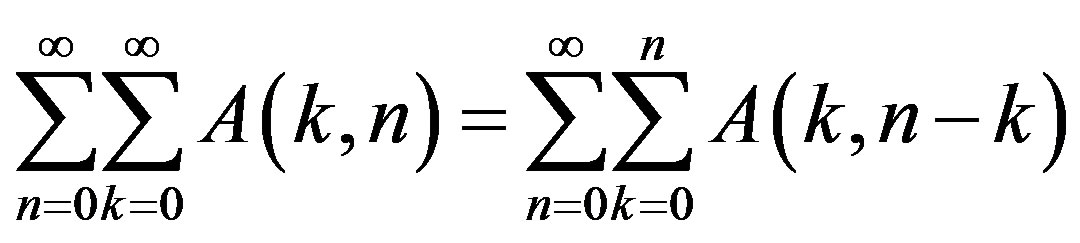 (3)
(3)
 (4)
(4)
and, for m is a positive integer such that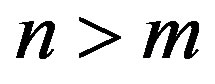 , then
, then
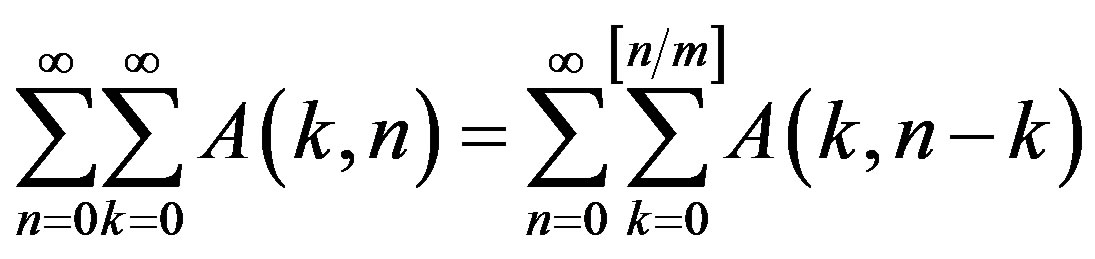 (5)
(5)
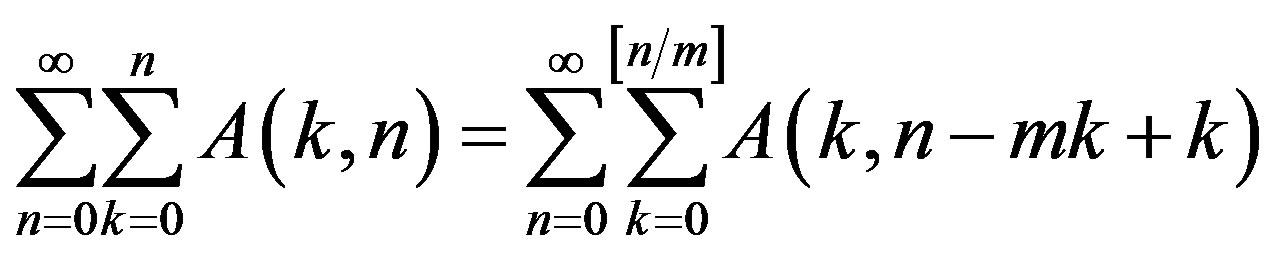 (6)
(6)
We define Humbert matrix polynomials of two variables and discuss its special cases. Some hypergeometric matrix representations of the Humbert matrix polynomials of two variables, the double generating matrix functions and expansions of the Humbert matrix polynomials of two variables in series of Hermite polynomials are given. Some particular cases are also discussed.
2. Definition of Humbert Matrix Polynomials of Two Variables
Let A be a positive stable matrix in 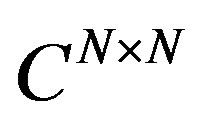 for a positive integer m, we define Humbert matrix polynomials by
for a positive integer m, we define Humbert matrix polynomials by
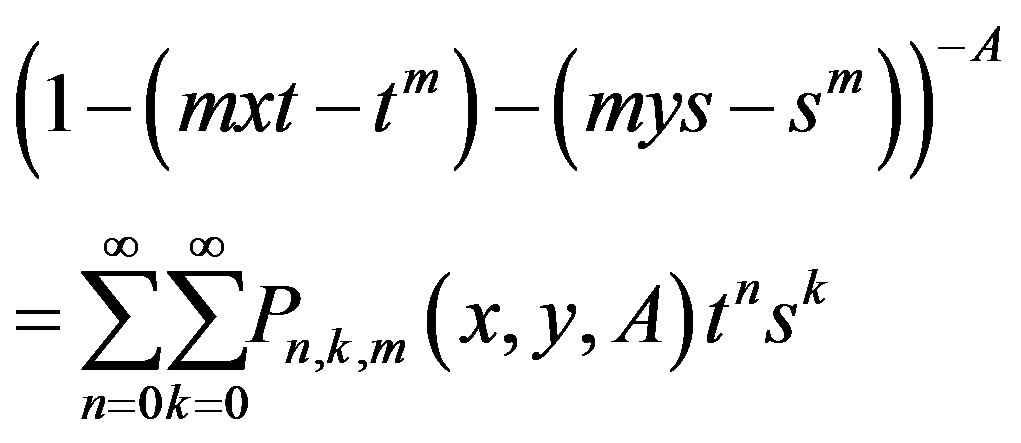 (7)
(7)
Now (7) it can be written in the form
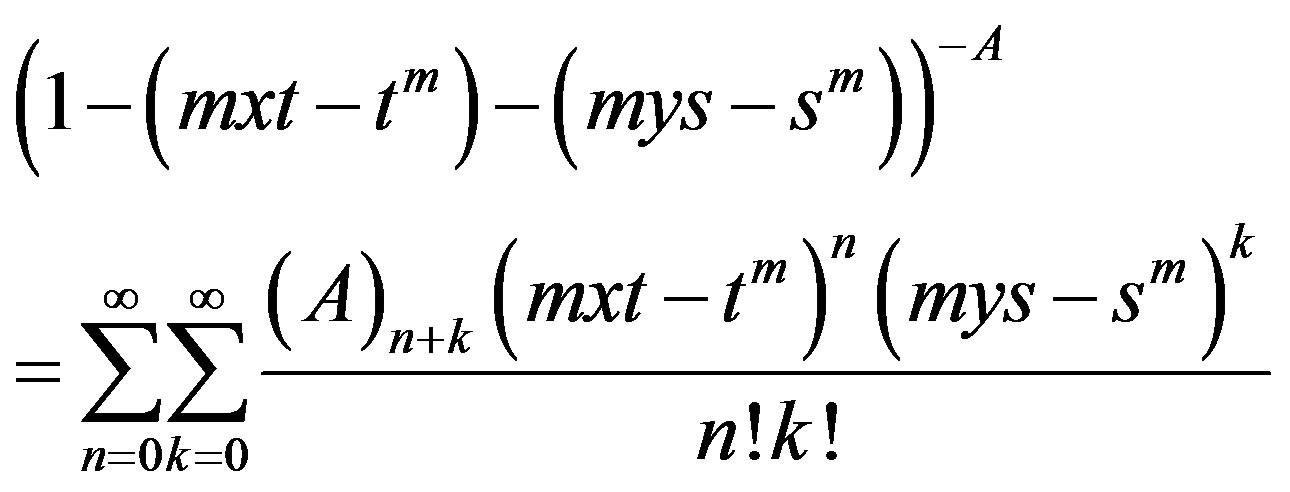
and by (3) and (6) respectively, one gets

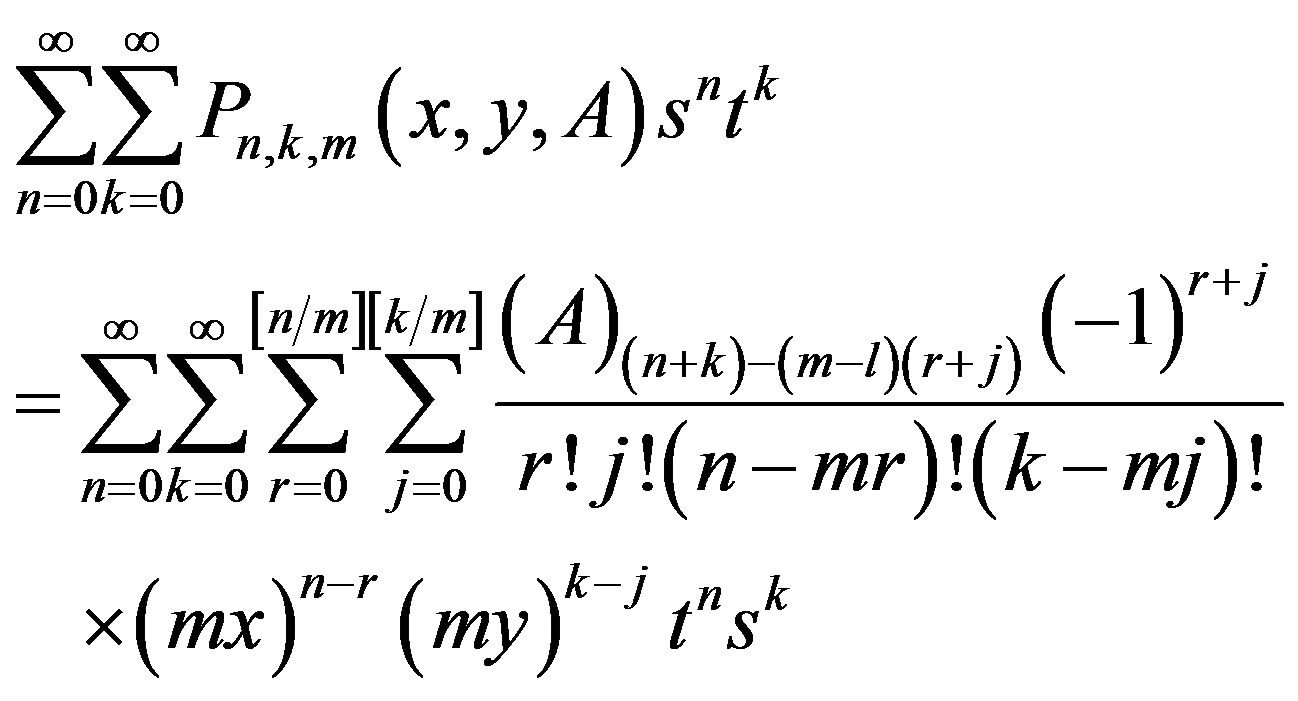 (8)
(8)
By equating the coefficients of 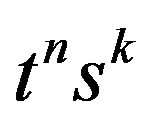 in (7) and (8), we obtain an explicit representation of the Humbert matrix polynomials of two variables. In the form
in (7) and (8), we obtain an explicit representation of the Humbert matrix polynomials of two variables. In the form
 (9)
(9)
from which it follows that 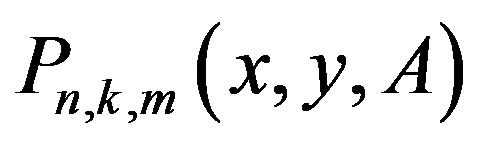 is a matrix polynomial in two variables x and y of degree precisely n in x and k in y. In (9) setting m = 2, we get the Gegenbauer matrix polynomials of two variables [13] as particular case of the Humbert matrix polynomials of two variables.
is a matrix polynomial in two variables x and y of degree precisely n in x and k in y. In (9) setting m = 2, we get the Gegenbauer matrix polynomials of two variables [13] as particular case of the Humbert matrix polynomials of two variables.
3. Hypergeometric Matrix Representation for 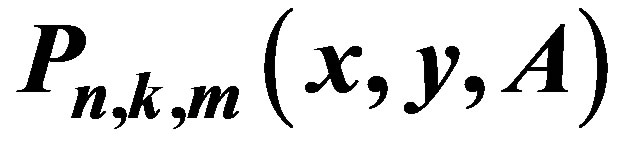
We study here the representation of the hypergeometric matrix representation for the Humbert matrix polynomials of two variables. There are some facts and notations used throughout the development in Sections 3 - 5, which are listed here.
Fact 1. [15] The reciprocal scalar Gamma Function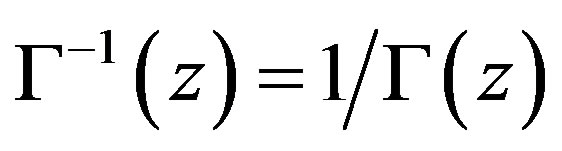 , is an entire functions of the complex variable z. Thus, for
, is an entire functions of the complex variable z. Thus, for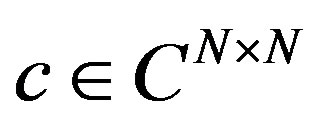 , the Riesz-Dunford functional calculus [11] shows that
, the Riesz-Dunford functional calculus [11] shows that 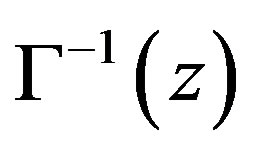 is well defined and is indeed, the inverse of
is well defined and is indeed, the inverse of , Hence: if
, Hence: if 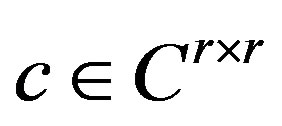 is such that
is such that 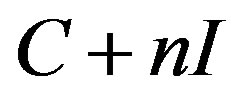 is invertible for every integer
is invertible for every integer . Then
. Then
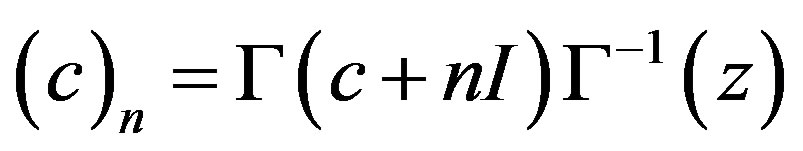 .
.
Fact 2. [12] If A, B and C are members of 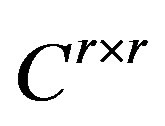 for which
for which 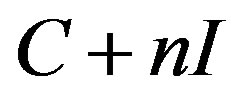 is invertible for every integer
is invertible for every integer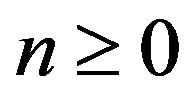 . The hypergeometric matrix function
. The hypergeometric matrix function 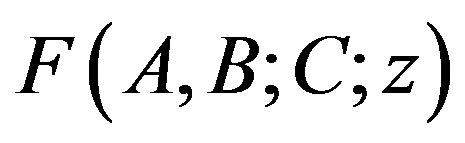 is defined by
is defined by
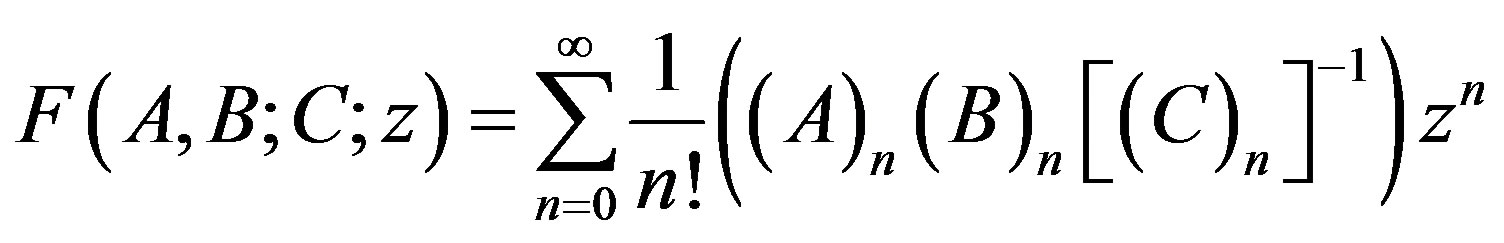
it converges for .
.
Notation 1. [16] For , the matrix version of the pochhammer symbol (the shifted factorial) is
, the matrix version of the pochhammer symbol (the shifted factorial) is
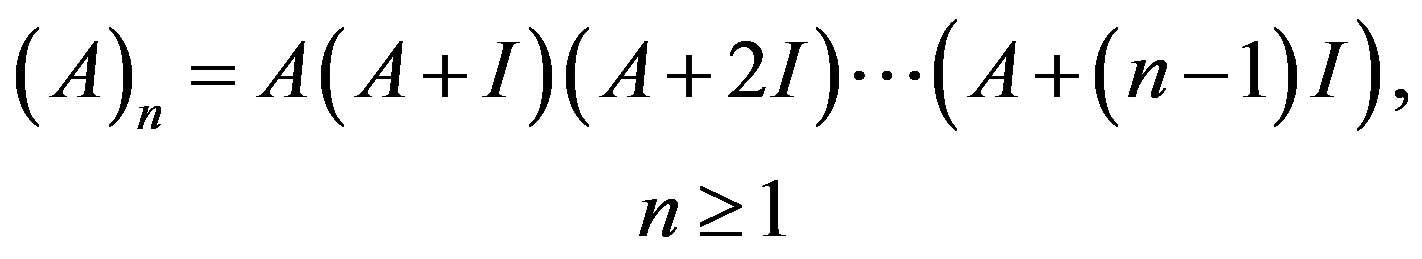 (10)
(10)
with .
.
Note that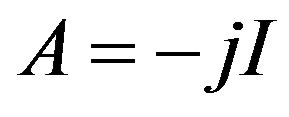 , where j is a positive integer, then
, where j is a positive integer, then 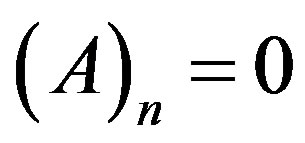 when ever
when ever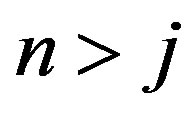 . Also, the product in (10) is commutative, and then it is easy to see that
. Also, the product in (10) is commutative, and then it is easy to see that


and
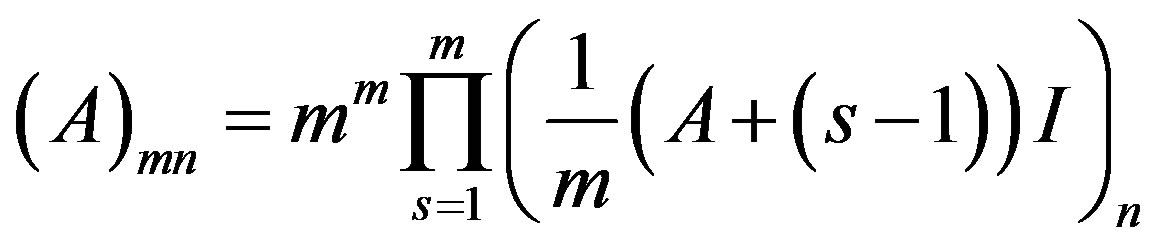
where m is a positive integer.
Notation 2. [17]

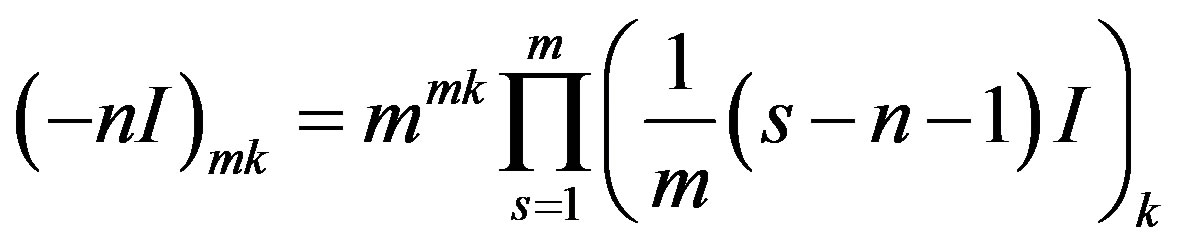
Now, in view of Notation 2, the explicit representation (9) for , becomes
, becomes
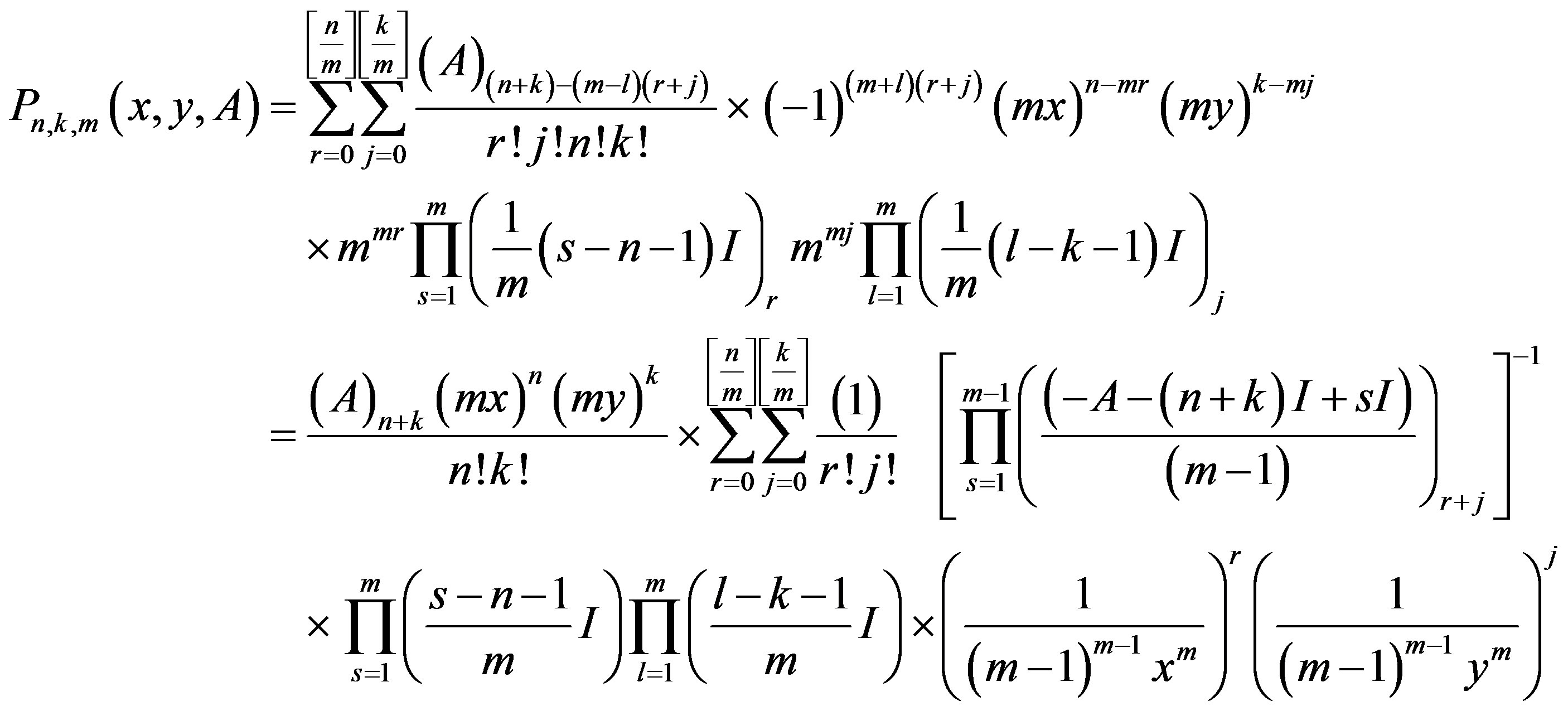
Thus we get the following hypergeometric representation of Humbert matrix polynomials of two variables.
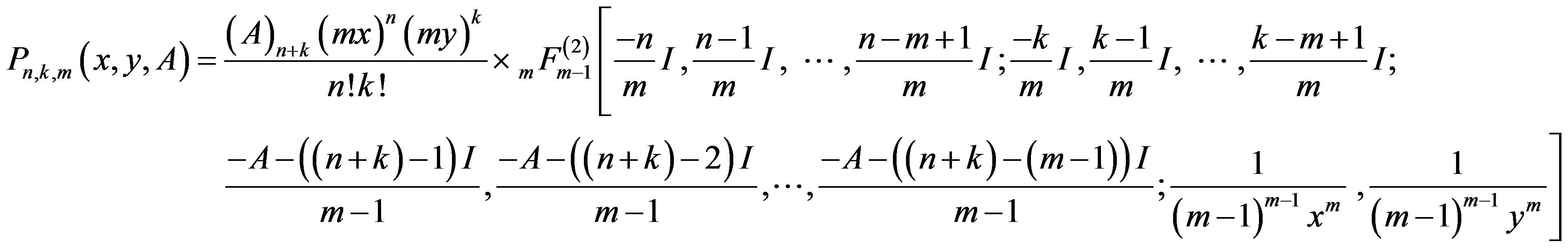 (11)
(11)
For m = 2 (11), we gives hypergeometric representation of Gegenbauer matrix polynomials of two variables [13].
The above facts and notations will be used throughout the next two sections.
4. Additional Double Generating Matrix Functions
Now, since
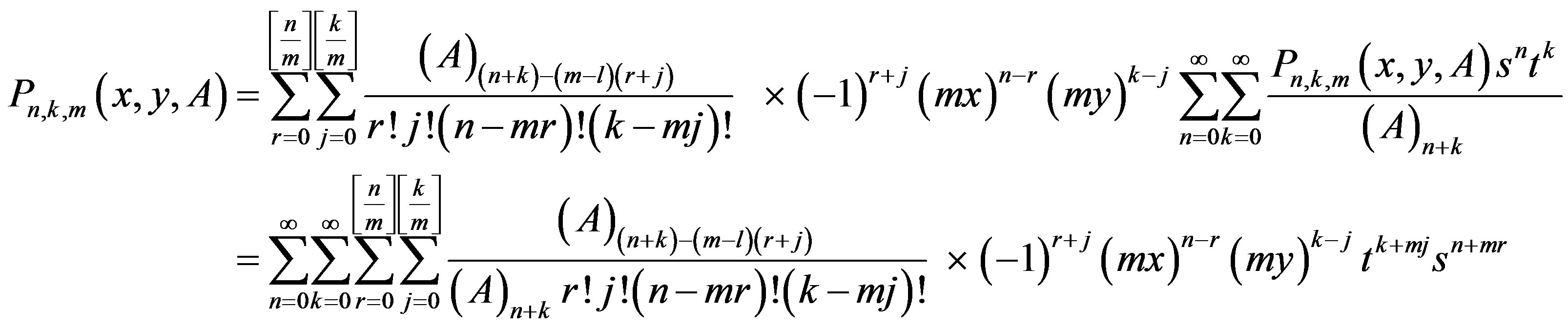 (12)
(12)
By using (5), one gets
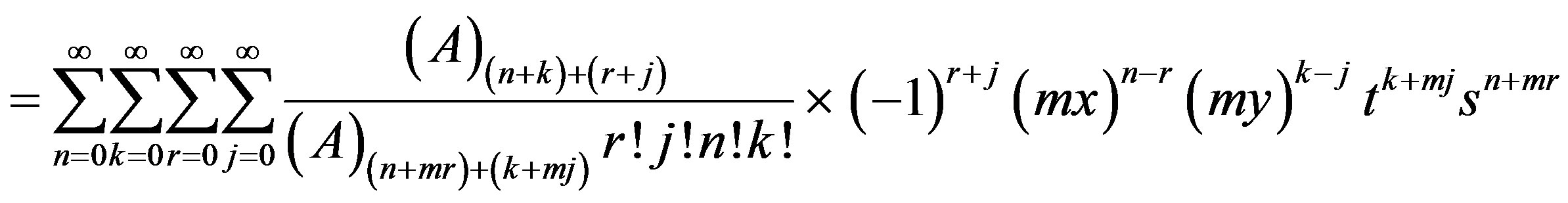 (13)
(13)
By using Notation 1, the following generating matrix functions for Humbert matrix polynomials of two variables follows
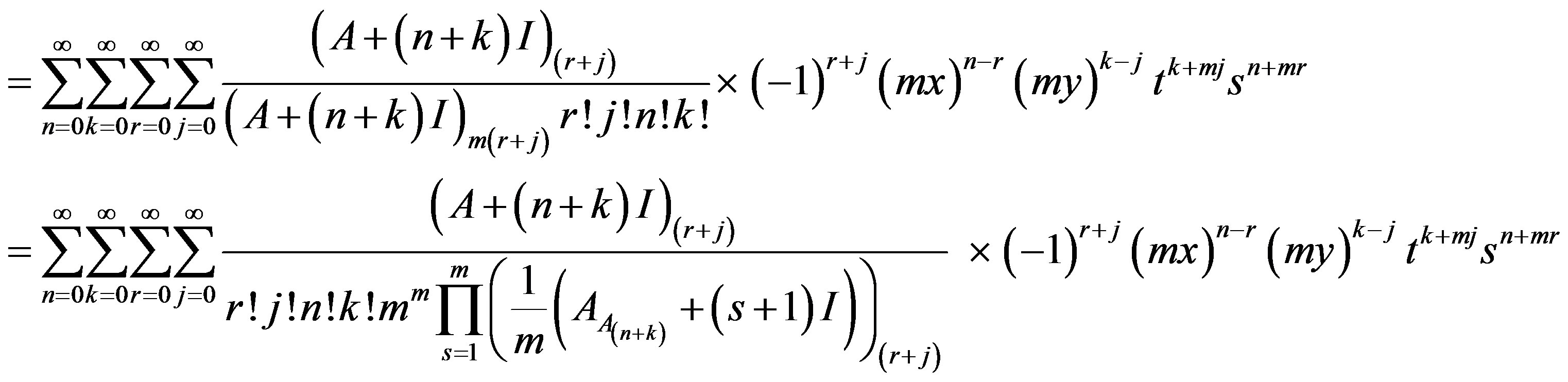

have thus discovered the family of double generating function of the Humbert polynomials of two variables
 (14)
(14)
If B is a positive stable matrix in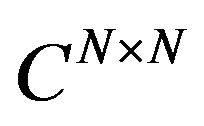 , then let us now return to (12) and consider the double sum.
, then let us now return to (12) and consider the double sum.
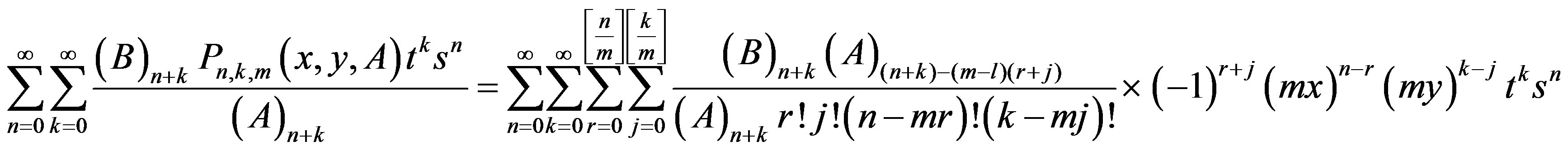
Then in similar manner, we get
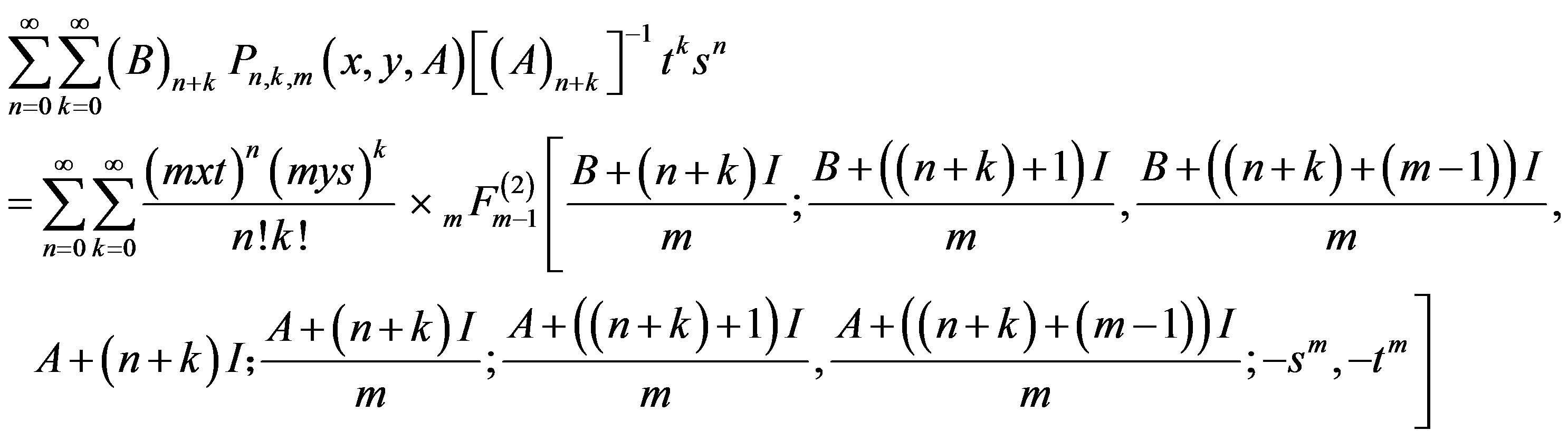 (15)
(15)
5. Expansions of 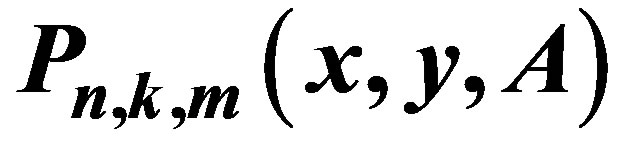 in Series of Hermite
in Series of Hermite 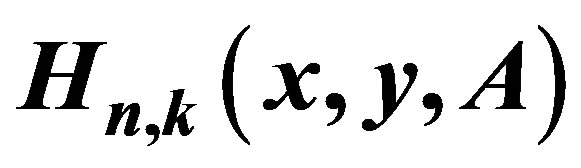
Now, we derive expansions of  in series of Hermite
in series of Hermite  According to [18], the expansion of
According to [18], the expansion of 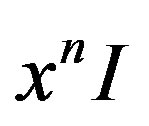 in a series of Hermite matrix polynomials was given in the form:
in a series of Hermite matrix polynomials was given in the form:
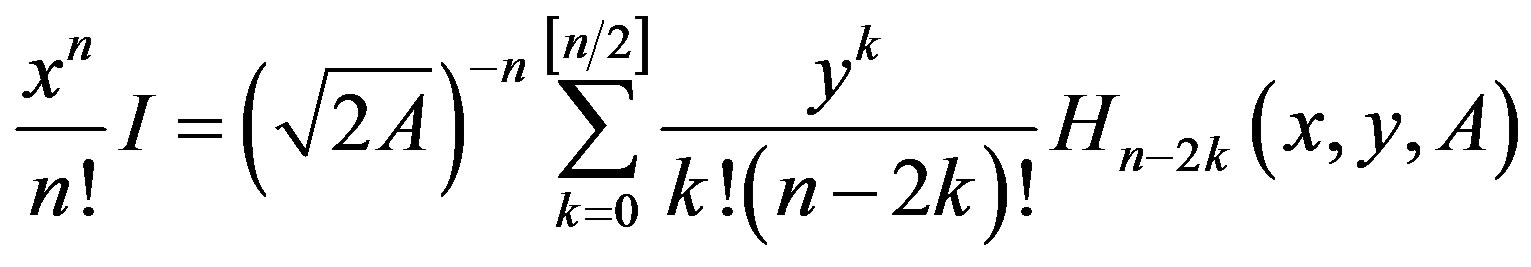 (16)
(16)
which with the aid of (5) and (9), one gets
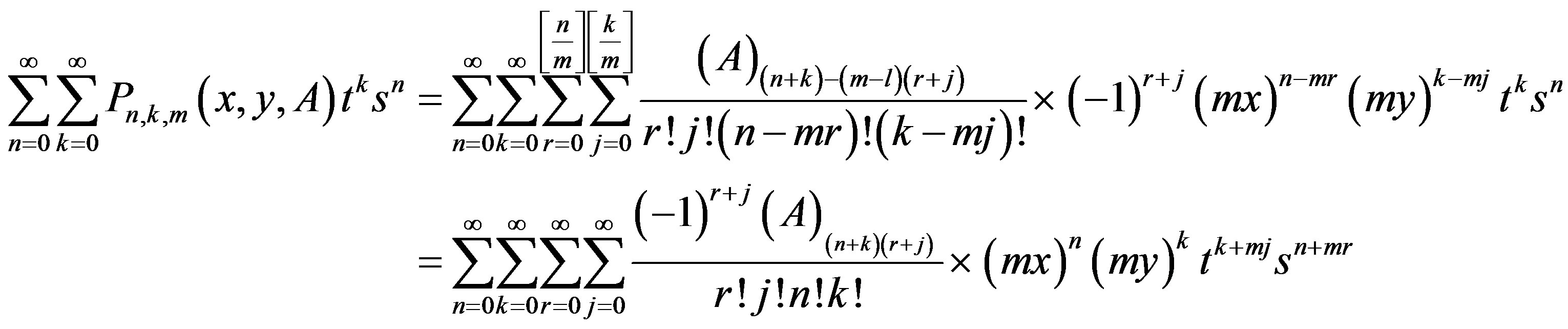
From (16), we get
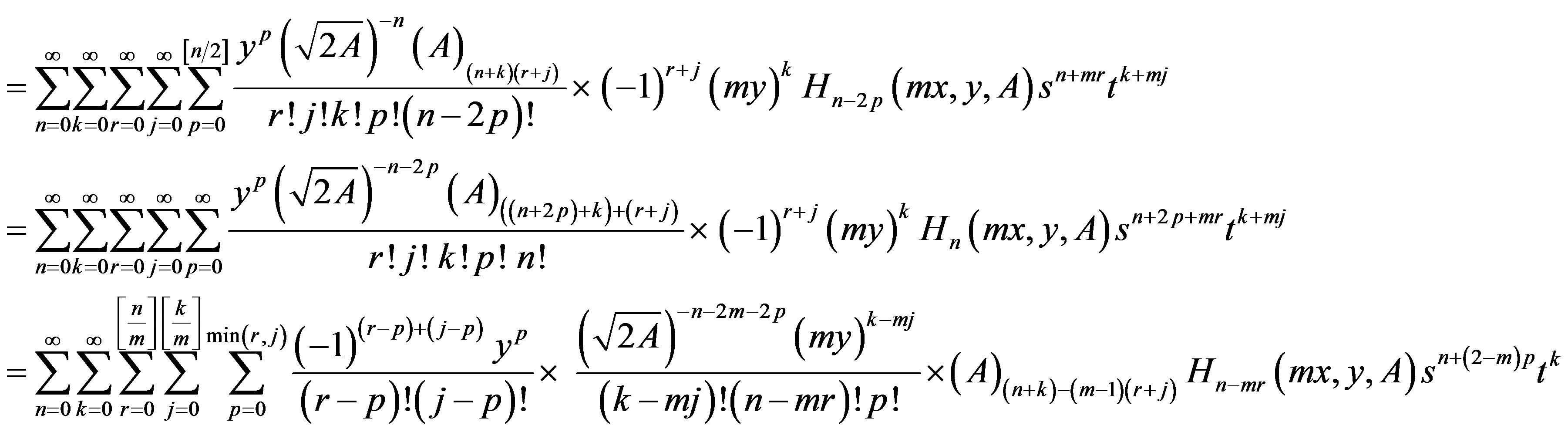
Now replacing  by
by 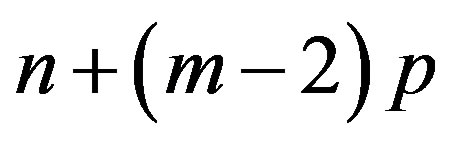 and equating the coefficients of
and equating the coefficients of 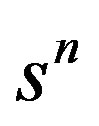
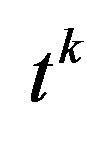 , we get
, we get
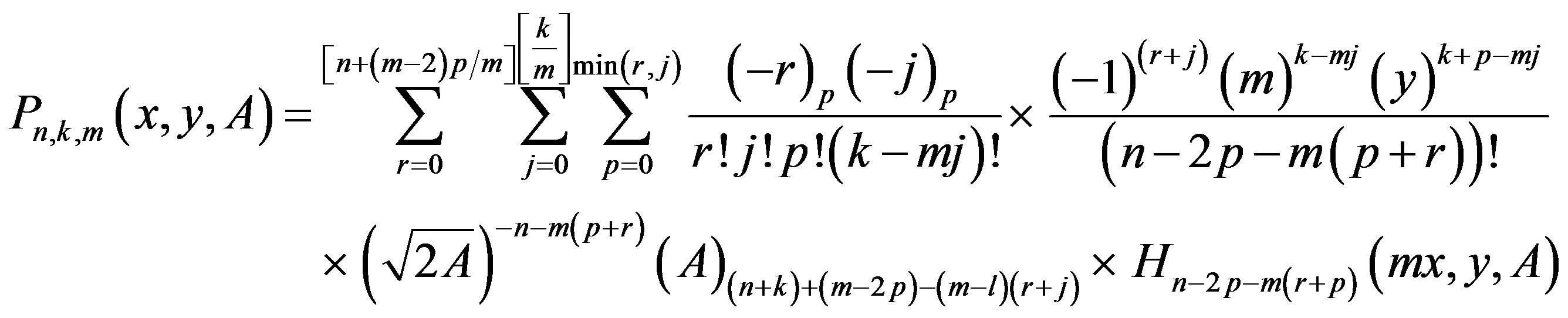 (17)
(17)
REFERENCES
- A. G. Constantine and R. J. Mairhead, “Partial Differential Equations for Hypergeometric Functions of Two Argument Matrices,” Journal of Multivariate Analysis, Vol. 2, No. 3, 1972, pp. 332-338. doi:10.1016/0047-259X(72)90020-6.
- R. J. Muirhead, “Systems of Partial Differential Equations for Hypergeometric Functions of Matrix Argument,” Annals of Mathematical Statistics, Vol. 40, No. 3, 1970, pp. 991-1001. doi:10.1214/aoms/1177696975
- A. Terras, “Special Functions the Symmetric Space of Positive Matrices,” SIAM Journal on Mathematical Analysis, Vol. 16, No. 3, 1985, pp. 620-640. doi:10.1137/0516046
- A. T. James, “Special Functions of Matrix and Single Argument in Statistics in Theory and Application of Special Functions,” Academic Press, New York, 1975.
- A. J. Duran, “Markov’s Theorem for Orthogonal Matrix Polynomials,” Canadian Journal of Mathematics, Vol. 48, 1996, pp. 1180-1195. doi:10.4153/CJM-1996-062-4
- A. J. Duran and W. Van Assche, “Orthogonal Matrix Polynomials and Higher Order Recurrence Relations,” Linear Algebra and Its Applications, Vol. 219, No. 1, 1995, pp. 261-280. doi:10.1016/0024-3795(93)00218-O.
- L. Jódar and J. Sastre, “The Growth of Laguerre Matrix Polynomials on Bounded Inervals,” Applied Mathematics Letters, Vol. 13, No. 8, 2000, pp. 21- 26. doi:10.1016/S0893-9659(00)00090-2.
- L. Jódar, R. Company and E. Navarro, “Laguerre Matrix Polynomials and Systems of Second Order Differential Equations,” Applied Numerical Mathematics, Vol. 15, No. 1, 1994, pp. 53-63. doi:10.1016/0168-9274(94)00012-3.
- A. Sinap and W. Van Assch, “Orthogonal Matrix Polynomials and Applications,” Journal of Computational and Applied Mathematics, Vol. 66, No. 1-2, 1996, pp. 27-52. doi:10.1016/0377-0427(95)00193-X.
- S. Saks and A. Zygmund, “Analytic Functions,” Elsevier, Amsterdam, 1971.
- N. Dunford and J. Schwartz, “Linear Operators, Part I,” Interscience, New York, 1955.
- L. Jódar and J. C. Cortés, “On the Hypergeometric Matrix Function,” Journal of Computational and Applied Mathematics, Vol. 99, No. 1-2, 1998, pp. 205-217. doi:10.1016/S0377-0427(98)00158-7
- G. S. Khammash, “A Study of a Two Variables Gegenbauer Matrix Polynomials and Second Order Partial Matrix Differential Equations,” International Journal of Mathematical Analysis, Vol. 2, No. 17, 2008, pp. 807-821.
- E. Defez and L. Jódar, “Some Applications of the Hermite Matrix Polynomials Series Expansions,” Journal of Computational and Applied Mathematics, Vol. 99, No. 1-2, 1998, pp. 105-117. doi:10.1016/S0377-0427(98)00149-6.
- E. Hille, “Lectures on Ordinary Differential Equations,” Addison-Wesley, New York, 1969.
- L. Jódar and J. C. Cortés, “Some Properties of Gamma and Beta Matrix Functions,” Applied Mathematics Letters, Vol. 11, No. 1, 1998, pp. 89-93. doi:10.1016/S0893-9659(97)00139-0
- E. D. Rainvlle, “Special Functions,” Chelsea Publishing Co., Bronx, New York, 1960.
- R. S. Batahan, “Anew Extension of Hermite Matrix Polynomials and Its Applications,” Linear Algebra and Its Applications, Vol. 419, No. 1, 2006, pp. 82-92. doi:10.1016/j.laa.2006.04.006

