World Journal of Condensed Matter Physics
Vol.3 No.4(2013), Article ID:40108,5 pages DOI:10.4236/wjcmp.2013.34036
The Temperature Dependence of the Density of States in Semiconductors
![]()
1Namangan Engineering Pedagogical Institute, Namangan, Uzbekistan; 2Namangan Engineering Institute of Technology, Namangan, Uzbekistan.
Email: gulyamov1949@mail.ru
Copyright © 2013 Gafur Gulyamov et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 17th, 2013; revised October 21st, 2013; accepted November 10th, 2013
Keywords: Band Gap; The Effective Mass Density of States; The Energy Spectrum; The Numerical Simulation and Experiment
ABSTRACT
The temperature dependence of the density of energy states in semiconductors is considered. With the help of mathematical modeling of the thermal broadening of the energy levels, the temperature dependence of the band gap of semiconductors is studied. In view of the non-parabolic and the temperature dependence of the effective mass of the density of states in the allowed bands, graphs of temperature dependence of the band gap are obtained. The theoretical results of mathematical modeling are compared with experimental data for Si, InAs and solid solutions of p-Bi2−xSbxTe3−ySey. The theoretical results satisfactorily explain the experimental results for Si and InAs. The new approach is investigated by the temperature dependence of the band gap of semiconductors.
1. Introduction
Density of states determines thermal, optical, magnetic, electric and other physical properties of semiconductors. The change of the energy gaps with increasing temperature can be explained by the influence of lattice vibrations on the energy levels in crystals. Statistical analysis of the problem is carried out by analyzing the free energy of the crystal as the sum of the energies of the electron gas, lattice vibrations and electron-phonon interactions [1, 2]. On the other hand, one should take into account the thermal broadening of the energy levels of the radiative transitions [1,2]. In [3-8] the temperature dependence of the density of states is determined by relaxation spectroscopy of energy levels in semiconductors. It is shown that the density of surface states varies according to temperature. Due to the thermal broadening of the levels, the discrete spectrum with hanging temperature becomes a continuous energy spectrum. With the expansion of the energy spectrum of the density of states in the energy derived from the probability required energy level, it was shown that the amount of energy slits is dependent on temperature. The temperature dependence of the band gap is determined by the density of states of the conduction band and valence band of the semiconductor. Due to the thermal broadening of the density of states near the bottom of the conduction band, valence band reduces band gap. In the calculation of the temperature dependence of the forbidden assumed for simplicity, the density of states in the areas of constant edge of the conduction band and valence band is sharp and has a stepped shape. In these works, the effective mass of the density of states does not depend on the temperature. However, as shown in experiments [9], the effective mass of the density of states depends on the temperature. This change in the effective mass changes the temperature dependence of the band gap. However, in the real state of the semiconductor, density is a function of speed and energy band structure of the sample is determined. Moreover, the density of states is so general that it can be used even when there is no Brillouin zone and sharp boundaries of permitted and prohibited zones [10,11].
Thus, the analysis of experimental results for comparison between theory and experiment is necessary to consider the specific form of the band structure of the semiconductor and the dependence of the effective mass of the charge carriers of the temperature.
The aim of this work is to study the temperature dependence of the band gap semiconductor with the band structure and temperature dependence of the effective mass of carriers and comparison of theory with experiment.
2. The Dependence of the Energy Gap with Temperature
As was shown in [3-8], the density of states can be decomposed into a series of GN functions. The temperature dependence of GN function will determine the statistical thermal broadening of the discrete levels. The resulting density of states is determined by the expansion of discrete states by GN-function takes into account the thermal broadening of each discrete level. We assume that the density of states at absolute zero parabolic Ns(E). We define a specific form of the electron dispersion. For example, the electron dispersion parabola or according to the Kane model. According to the procedure [3-8] we expand the density of states in a series of GN-functions. We will take into account nonparabolicity zones via the temperature dependence of the effective mass of the temperature:
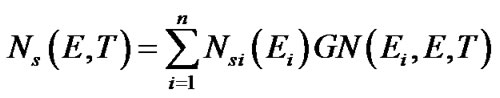 (1)
(1)
where
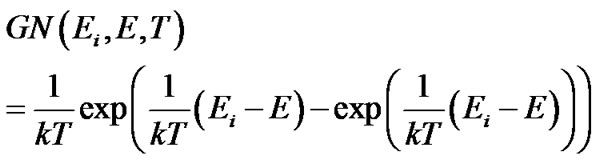
Ns(E)—the density of states at zero temperature [12, 13]
 (2)
(2)
where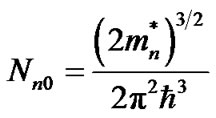 ,
, 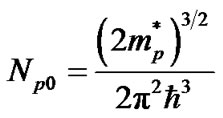 and Ec, Ev—
and Ec, Ev—
The value of the energy of the conduction band and valence band at T = 0.
Substituting (2) into (1) we obtain the density of states at temperature T. In determining the width of the gap, we use the density of states, which depends on temperature. When modeling the process of measuring the width of the band gap with increasing temperature, use the condition given in [8]. We assume that the density of states corresponding to the energy band gap edges Ec and Ev is Nk. Energy region where the density of states Ns(T) is less than the critical Nk assume band gap. The energy range where Ns(T) > Nk permission from the zones. The values of the edges of the band gap position of the bottom of the conduction band Ec(T) and valence bands Ev(T) is determined by the solution of the equation transcendent
 (3)
(3)
transcendent solution of Equation (3) with respect to E at the specified temperature T, and the critical value of the density of states Nk determines the position of the edges of the gap Ec(Nk, T) and Ev(Nk, T). In Equation (3) Nk included as a parameter. Nk value is determined by the condition of the experiment and by the accuracy of measurement techniques. Then the band gap is defined as the difference between the values of Ec(T, Nk) and Ev(T, Nk):
 (4)
(4)
It follows that the method of determining the accuracy of the experiment and the important factors in determining the width of the gap. Indeed the band gap, determined by optical methods, “optical width” of the band gap can not match the value of the band gap, determined by the temperature dependence of the resistance of the semiconductor. One of the reasons is that different values for Nk optical and electrical measuring techniques.
3. The Influence of the Effective Mass of the Density of States at the Temperature Dependence of the Band Gap in Solid p-Bi2−xSbxTe3−ySey
In [9] found that in solid p-Bi2−xSbxTe3−ySey effective density of states in the valence band is strongly dependent on temperature. Figure 1 shows the temperature dependence of the effective mass of the density of states in solid p-Bi2−xSbxTe3−ySey from [9]. Using the data of Figure 1 calculated by the model bandgap variation with temperature.
Figure 2 shows plots of the density of states at a temperature T = 100 K and T = 300 K. As can be seen from Figure 2 into account the change of the effective mass density of states significantly affects the density of states near the valence band.
Figure 3 shows the temperature dependence of the graphics of the band gap for the solid solutions pBi2−xSbxTe3−ySey to changing the effective mass density of states taken from Figure 3 [9]. For example, for a solid solution of p-Bi2−xSbxTe3−ySey change in the band gap by changing the effective mass at T = 100 K is
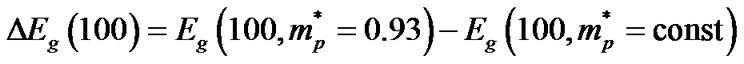
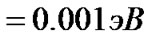 . By increasing the temperature to T = 300 K, changing the width of the band gap due to change in the effective mass of the density of states is
. By increasing the temperature to T = 300 K, changing the width of the band gap due to change in the effective mass of the density of states is 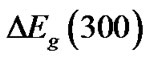
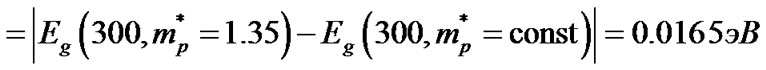
This shows that the reduction of the band gap by changing the effective mass with increasing temperature from
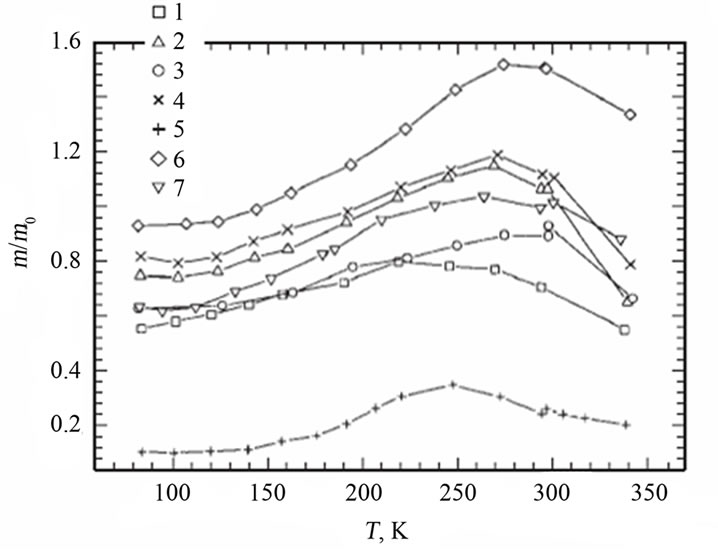
Figure 1. The temperature dependence of the effective mass of the density of states m/m0 in solid solutions p-Bi2−xSbxTe3−ySey [14]. 1→ x = 1, y = 0.06; 2→ x = 1.1, y = 0.06; 3→ x = 1.2, y = 0.06; 4→ x = 1.2, y = 0.09; 5→ x = 1.3, y = 0.09, 6→ x = 1.3, y = 0.07; 7→ x = 1.5, y = 0.09.

Figure 2. Graphic density of states at T = 100 K and 300 K.  and
and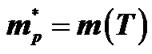 . ______
. ______ 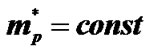 ------
------ 
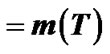 .
.
100 K to 300 K can be increased more than tenfold. Figure 3 shows plots of the temperature dependence of the band gap of the solid solutions p-Bi2−xSbxTe3−ySey for the changes in the effective mass of the density of states taken from Figure 1. Thus, changes in the effective mass of the density of states with temperature can greatly affect the temperature dependence of the band gap.
4. Comparison of Theory with Experiment
The temperature dependence of the width of the energy gap depends on the density of states at the absolute temperature. In the model used in [3-8] the temperature dependence of the density of states is determined by the temperature dependence of GN-functions and band structure of the allowed bands at the bottom of the conduction
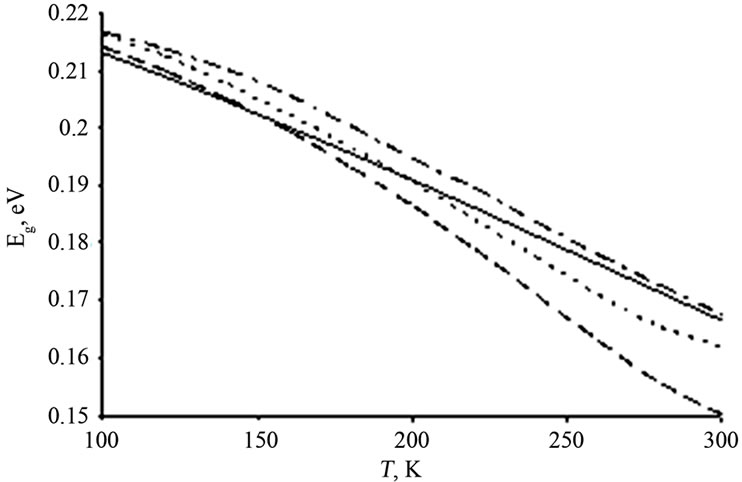
Figure 3. Graphic Eg(T)—temperature dependence of the band gap. 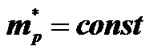 и
и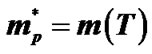 . _____
. _____ ; ----
; ---- , p-Bi0.7Sb1.3Te2.93Se0.07; ......
, p-Bi0.7Sb1.3Te2.93Se0.07; ...... , p-Bi0.6Sb1.2Te2.91Se0.09; ·-·-·-·-
, p-Bi0.6Sb1.2Te2.91Se0.09; ·-·-·-·- , p-Bi0.5Sb1.5Te2.91Se0.09.
, p-Bi0.5Sb1.5Te2.91Se0.09.
band and at the top of the valence band. Analysis of the results of numerical modeling of changes in the density of states at the temperature showed that the value of the density of states near the band edges is determined by the number of states of the band edges, a few tens of kT or about 0.1 meV, the density of states in the depths of the allowed zones does not affect the width of the gap. Since the GN-function of deep area of the zone does not penetrate into the region band gap semiconductor, the main contribution to the shift of the band edges give the states lying close to the edges of the allowed bands. According to this law of dispersion near the top of the valence band and the conduction band edge is crucial in determining the temperature dependence of the band gap Eg(T). Figures 4 and 5 are graphs of temperature dependence of the band gap of InAs [14] and Si [15].
Using mathematical modeling of the temperature dependence of Eg(T) for a parabolic band and Kane model obtained plots of the band gap of the temperature. As can be seen in the investigated temperature range of parabolic dispersion and a model for the use of Kane’s model is in good agreement with experimental data for InAs [14] and Si [15]. Theoretical calculations of the theoretical given for these materials is in good agreement with the experimental data. It follows that the temperature dependence of the band gap is satisfactorily described by a mathematical model of expansion of the density of states in a series of GN-functions, which describes the temperature dependence of the thermal broadening of individual energy levels in the zones and in the forbidden zone.
5. Conclusion
The temperature dependence of the energy spectrum of the density of states of solid solutions of
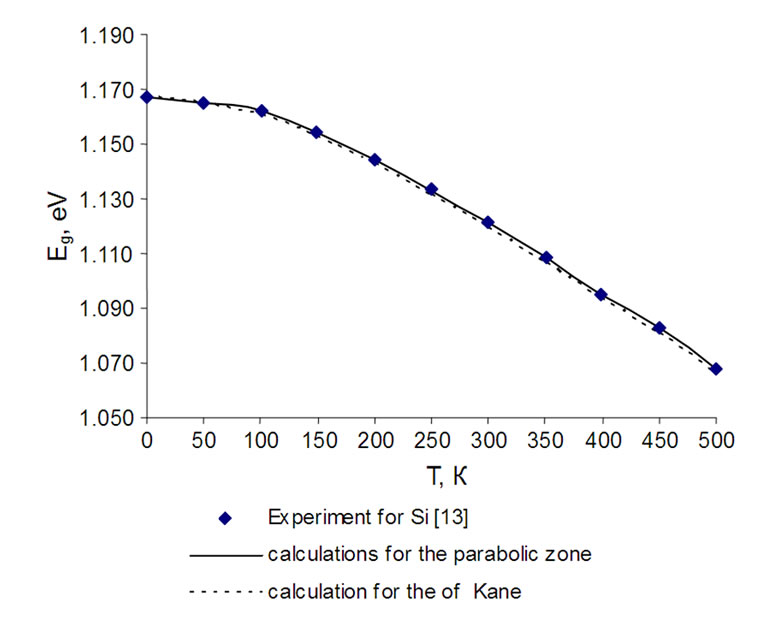
Figure 4. The temperature dependence of the band gap of Si.
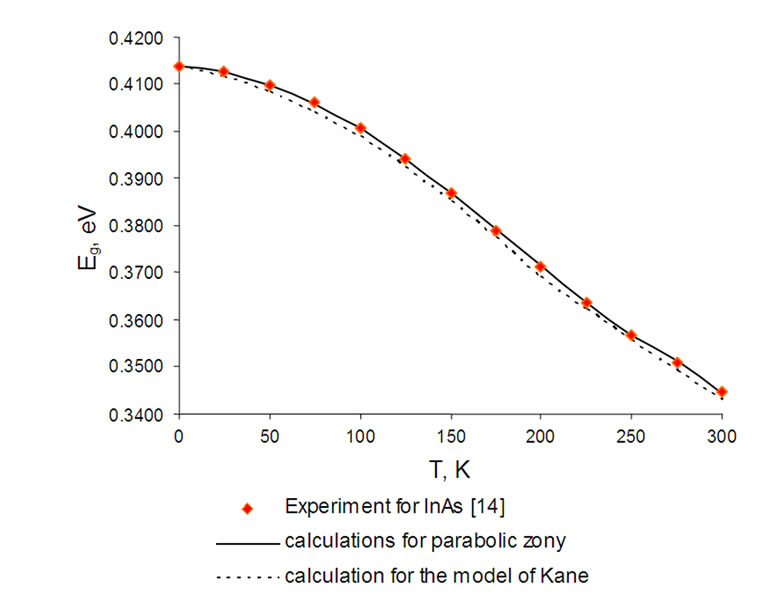
Figure 5. The temperature dependence of the band gap of InAs.
p-Bi2−xSbxTe3−ySey takes into account of the temperature dependence of the effective mass of the density of states in the valence band. The temperature dependence of the band gap for the changes in the effective mass of the density of states is obtained. The numerical experiments show that at temperatures T > 120 K, change in the effective mass of the density of states by increasing T has significant effect on the temperature dependence of the band gap.
In this temperature range ([0, 300 K], [0, 500 K]), mathematical modeling of the temperature dependence of the band gap is satisfactorily described by a parabolic dispersion law and the Kane model. The experimental results of changing the band gap of silicon [13] and InAs [14] within the accuracy of measurement is consistent with the results of theoretical calculations. Comparison of theory and experiment shows that the thermal broadening of the energy levels with the GN function satisfactorily describes the process of the temperature dependence of the band gap of Si and InAs.
REFERENCES
- B. Ridley, “Quantum Processes in Semiconductors,” Clarendon Press, Oxford, 1982.
- R. Pässler, “Semi-Empirical Descriptions of Temperature Dependences of Band Gaps in Semiconductors,” Physica Status Solidi (b), Vol. 236, No. 3, 2003, pp. 710-728. http://dx.doi.org/10.1002/pssb.200301752
- G. Gulyamov and N. Yu. Sharibaev, “Determination of the Density of Surface States at the Semiconductor-Insulator Interface in a Metal-Insulator-Semiconductor Structure,” FTP (Fizika Technika Poluprovodnikov), Vol. 45, No. 2, 2011, pp. 178-182.
- G. Gulyamov and N. Yu. Sharibaev, “Determination of the Discrete Spectrum of Surface State Density in MOSStructures Al-SiO2-Si Irradiated by Neutrons,” Poverkhnost’. Rentgenovskie, Sinkhrotronnye i Neitronnye Issledovaniya, No. 9, 2012, pp. 13-17.
- G. Gulyamov, N. Yu. Sharibaev and U. I. Erkaboev, “Thermal Broadening Density of States and Temperature Dependence of the Band Gap Ge,” FIP (Fyzicheckaya Injeneriya Poverkhnosti), Vol. 10, No. 4, 2012, pp. 366- 370.
- G. Gulyamov and N. Yu. Sharibaev, “Temperature Dependence of the Band Gap of Si and Due to the Thermal Broadening of the Density of States of,” FIP (Fyzicheckaya Injeneriya Poverkhnosti), Vol. 10, No. 2, 2012, pp. 4-8.
- G. Gulyamov, I. N. Karimov, N. Yu. Sharibaev and U. I. Erkaboev, “Determination of the Density of Surface States at the Semiconductor-Insulator Structures in Al-SiO2-Si and Al-SiO2-n-Si
at Low Temperatures,” Uzbek Journal of Physic, Vol. 12, No. 3, 2010, pp. 143-146. - G. Gulyamov, N. Yu. Sharibaev and U. I. Erkaboev, “Influence Effective Mass Density of States at Temperature Dependence of Band Gap in Solid Solutions p-Bi2−xSbxTe3−ySey,” FIP (Fyzicheckaya Injeneriya Poverkhnosti), Vol. 11, No. 2, 2013, pp. 195-198.
- L. N. Lukyanova, V. Kutasov and P. Konstantinov, “Effective Mass and Mobility in Solid p-Bi2−xSbxTe3−ySey for Temperatures <300K,” Solid State, Vol. 47, No. 2, 2005, pp. 224-228.
- N. Mott and E. Devis, “Electronic Processes in Non-Crystalline Materials,” 2nd Edition, Clarendon Press, Oxford, 1982.
- V. B. Bonch-Bruyevich, et al., “Electronic Theory of NonCrystalline Semiconductors,” Nauka, Moscow, 1981.
- A. I. Anselm, “Introduction to Semiconductor,” Nauka, Moscow, 1978.
- K. V. Shalimova, “Physics of Semiconductors,” Energoatomizdat, Moscow, 1985.
- A. M. R. Godenir, “Novel Dilute Nitride Semiconductor Materials for Mid-Infrared Applications,” University of Lancaster, 2008.
- A. Caiafa, X. Wang, J. L. Hudgins, E. Santi and P. R. Palmer, “Cryogenic Study and Modeling of IGBTS,” IEEE 34th Annual Power Electronics Specialist Conference, 15-19 June 2003, pp. 1897-1903.

