Atmospheric and Climate Sciences
Vol.3 No.4(2013), Article ID:36931,8 pages DOI:10.4236/acs.2013.34054
Granger Causality Analyses for Climatic Attribution
1Institute of Atmospheric Pollution Research, National Research Council (CNR), Monterotondo Stazione, Rome, Italy
2Department of Computer Engineering, Computer Science and Mathematics, University of L’Aquila, L’Aquila, Italy
Email: *pasini@iia.cnr.it
Copyright © 2013 Alessandro Attanasio et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 1, 2013; revised August 31, 2013; accepted September 7, 2013
Keywords: Granger Causality; Climatic Attribution; Global Warming; Forcings; Greenhouse Gases; Solar Radiation; Natural Variability
ABSTRACT
This review paper focuses on the application of the Granger causality technique to the study of the causes of recent global warming (a case of climatic attribution). A concise but comprehensive review is performed and particular attention is paid to the direct role of anthropogenic and natural forcings, and to the influence of patterns of natural variability. By analyzing both in-sample and out-of-sample results, clear evidences are obtained (e.g., the major role of greenhousegases radiative forcing in driving temperature, a recent causal decoupling between solar irradiance and temperature itself) together with interesting prospects of further research.
1. Introduction
The climate is a complex system characterized by several subsystems and many bidirectional relations between them. At present, the standard strategy to catch the complex behavior of climate is the application of dynamical modeling, using Global Climate Models (GCMs) and Regional Climate Models (RCMs): see [1] for the description of this dynamical approach and the conceptual and practical relevance of these simulations.
The problem of understanding and weighting the main causes of recent climate change is generally faced by numerical experiments within this modeling framework. The final aim of these studies is to evaluate if one is able to attribute this change to some specific causes out of a number of possibilities. The situation is quite complex but, at least as far as the attribution of global temperature changes is concerned (a case of climatic attribution), the results coming from dynamical models are quite clear and indicate that the fundamental causes of recent global warming are anthropogenic forcings (especially the increase of greenhouse gases in the atmosphere): a comprehensive review is provided in [2].
However, these dynamical models are very complex. In particular, just a limited number of processes, interactions and feedbacks can be considered and there are unavoidable uncertainties in attempting to simulate all of them in these standard climate models. The study of other complex systems has however shown that one often benefits from a change in viewpoint when analyzing them. There are complementary approaches in a number of other fields: e.g., in biology, the molecular biology approach vs. a more systemic point of view; in economy, the application of “traditional structural” models vs. the use of vector autoregressive (VAR) models.
Thus, a more data-driven approach can be fruitful in studies of climatic attribution, e.g. in assessing causeeffect relationships between external forcings and temperature behavior. In the past, for instance, neural network modeling has been applied for the attribution of global temperature (T) [3] and its results confirm the major role of anthropogenic forcings in driving T. Further researches have shown the usefulness of neural investigations for the attribution of temperature and precipitation at a regional scale, too [4,5].
In this framework, during the last years, analyses using the concept of Granger causality [6] have been performed to investigate the possible causal relations between external forcings and temperature behavior. In this paper we review the studies of climatic atttribution via this inferential method.
2. The Concept of Granger Causality
The concept of Granger causality is quite simple. Suppose that we have two variables, x and y. First, we attempt to forecast yt+1 using past terms of y. We then try to forecast yt+1 using past terms of x and y. We say that x Granger causes y, if the second forecast is found to be more successful, according to standard cost functions. If the second prediction is better, then the past of x contains a useful information for forecasting yt+1 that is not in the past of y. Clearly, Granger causality is based on precedence and predictability.
In a more formal way, we consider the vector time series 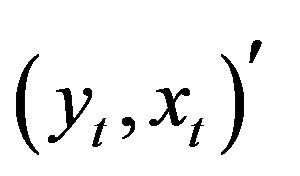 and the following information sets:
and the following information sets: 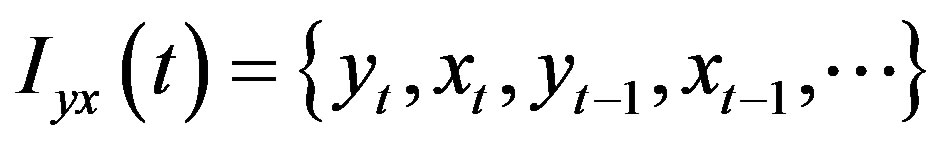 and
and 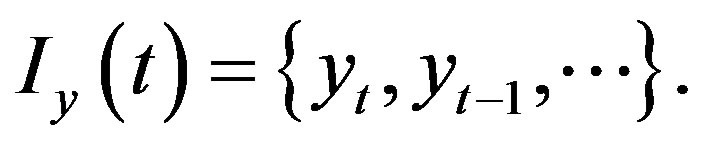 We denote with
We denote with 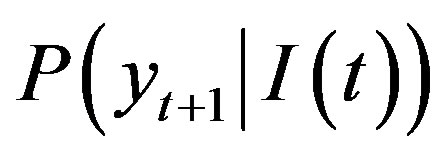 the optimal (minimum mean square error) linear forecast of the variable yt+1 based on the information set
the optimal (minimum mean square error) linear forecast of the variable yt+1 based on the information set . We say that x does not Granger cause y, in a bivariate system, if
. We say that x does not Granger cause y, in a bivariate system, if  for any t.
for any t.
In literature, the causal relationship between the variables x and y has often been investigated in a bivariate system. However, it is well known that in a bivariate framework problems of spurious causality and of noncausality due to omission of a relevant variable can arise. These problems can be solved if an auxiliary variable z is considered in the analysis, specifying a trivariate system.
We have that x does not Granger cause y, in a trivariate system, if 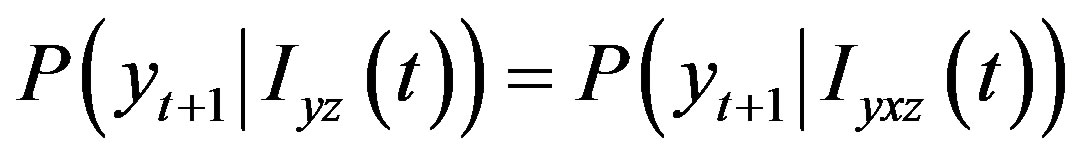 for any t, where
for any t, where 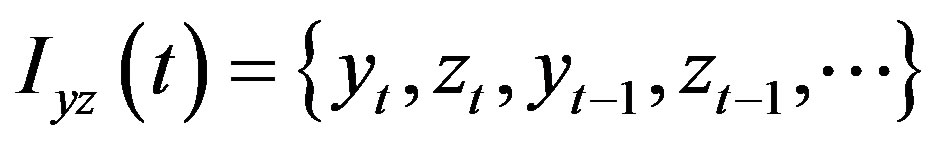 and
and 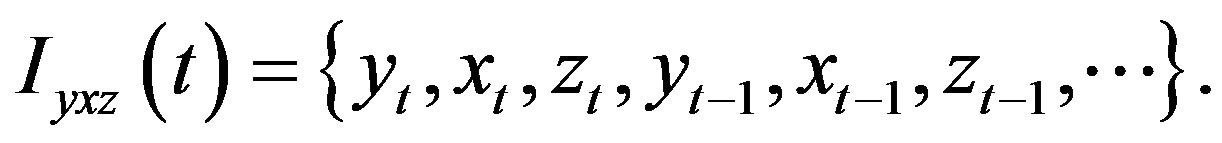
Suppose that the trivariate time series 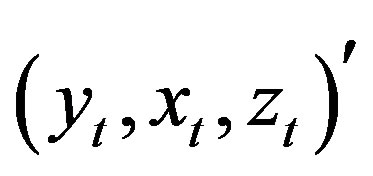 follows a vector autoregressive (VAR) model of finite order k:
follows a vector autoregressive (VAR) model of finite order k:
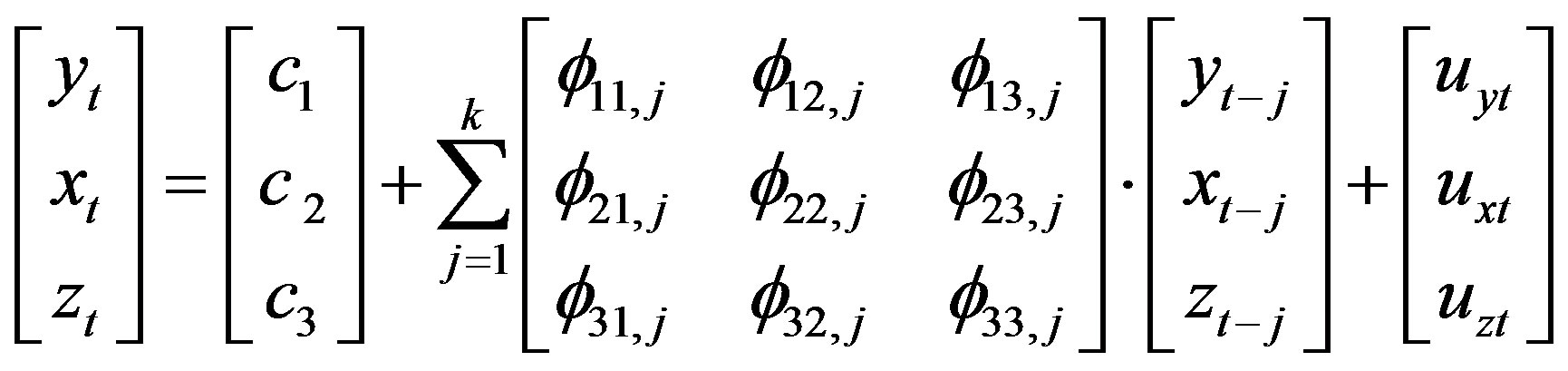 (1)
(1)
where 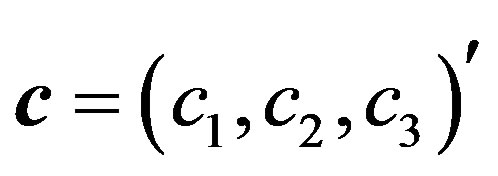 is a vector of constants,
is a vector of constants, 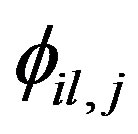 are fixed coefficients and
are fixed coefficients and  is a trivariate white noise process with nonsingular covariance matrix. In this framework, we have that x does not Granger cause y, with respect to the information set
is a trivariate white noise process with nonsingular covariance matrix. In this framework, we have that x does not Granger cause y, with respect to the information set , if and only if
, if and only if 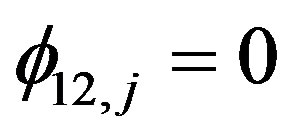 for
for 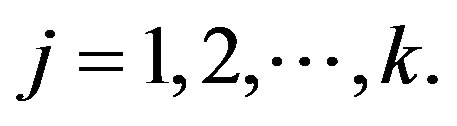 This characterization of the condition of noncausality is often used in literature to conduct the Granger causality tests.
This characterization of the condition of noncausality is often used in literature to conduct the Granger causality tests.
In what follows we mainly review the studies of climatic attribution performed by Granger causality analyses.
3. Granger Analyses in Specific Climatic Problems
During the last decade the notion of Granger causality has been used quite frequently in addressing specific causality problems in the climate system.
For instance, Diks and Mudelsee [7] analyzed the results of an ocean drilling program in order to estimate the causal relationships and directions among data about insolation, δ18O (a proxy for global ice volume) and δ13C (which reflects mainly the strength of formation of the so-called North Atlantic deep water).
Kaufmann et al. [8] used satellite data and a Granger causality analysis for estimating causal influences of snow cover and vegetation on temperatures in different seasons. In a further study, considered that the strength of Atlantic hurricanes is related to the sea surface temperatures (SST) of this ocean, Elsner [9,10] applied a Granger causality analysis to time series of global temperatures (GT) and SST and found a causal link from GT to SST, thus corroborating the hypothesis of changes induced by global warming.
Mosedale et al. [11] investigated SST effects on North Atlantic Oscillation (NAO)—an index which substantially drives the European winter climate—using data from simulations made with a coupled Global Climate Model (GCM). They showed that the so-called SST tripole index provides additional predictive information for the NAO than that available by using only past values of NAO, i.e. the SST tripole is Granger causal for the NAO.
Kaufmann et al. [12] studied the effect of urbanization and enlargement of towns on precipitation in a Chinese case study. They applied Granger causality and clearly found that, generally, urbanization causes a deficit in precipitation, even if differences for distinct seasons are detectable. Finally, Mohkov et al. [13] analyzed the relationship between El Niño Southern Oscillation (ENSO) and the strength of Indian monsoons. They found a bidirectional coupling which varies with time and this result shall be certainly useful for better understanding the dynamical mechanism behind this interaction.
The examples of application of Granger causality analyses just sketched show the potentiality of this technique in addressing causality problems in the climate system. Actually, however, in the realm of climate research there is a causality problem which overwhelms all other ones. It can be summarized in the question: what did cause the recent climate change or, at least, the recent global warming? Even considered the complexity of the climate system, which is the main external forcing that primarily induced the increase of temperature observed in the last century? Obviously, this is the main problem of attribution studies.
Given the potentialities of Granger analyses, it should not be a surprise that several studies have been performed by this technique in the framework of climatic attribution. In the next section we will describe those analyses conducted by a standard in-sample approach.
4. In-Sample Granger Analyses for Climatic Attribution and Their Problems
As a matter of fact, as the problem of global warming began to be recognized outside the field of climatologists, several analyses have been performed on the link between greenhouse gases and temperatures by several experts of statistical methods: see, for instance, [14,15] for two pioneering works.
More recently, even Granger causality has been specifically used by several researchers in order to analyze the causes of the recent rise in global temperature.
At our knowledge, the first paper dealing with this problem was written by Sun and Wang [16]. They analyzed time series of global CO2 emissions and global temperature anomalies, finding a strong numerical evidence that the increase in CO2 emissions causes global temperature change. Their approach is based on both direct Granger causality and cross-spectral analysis and the results of these two methods corroborate each other.
Kaufmann and Stern [17] assessed, in both directions, the linear causality between Southern Hemisphere temperature and Northern Hemisphere temperature, finding a Granger causation from South to North. After having included natural and anthropogenic forcings in the regressive models, they arrived at the conclusion that human activity played a major role in driving the historical record of temperature. In a strictly logical sense, however, other conclusions are possible in their study (see [18]). In fact, when the bivariate analysis is combined with a multivariate analysis, as in Kaufmann and Stern’s study, the results must be analyzed with great care.
Another study in which CO2 radiative forcing is considered in its causal relationship with temperature is that of Triacca [19], where, using the methodology of Toda and Yamamoto [20], he did not find any detectable linear Granger causality from CO2 to global temperature.
Even the influence of Sun on temperatures has been studied by the Granger technique. For instance, Reichel et al. [21] used a smoothed solar cycle length (SCL) as an index of long-term variability of Sun, estimated by spectral analysis of sunspot counts at different data frequencies. Another index of solar activity used by these researchers was total solar irradiance (TSI). In both cases they found a significant Granger causality from indices of solar activity to temperatures in their in-sample tests.
Even Mohkov and Smirnov [22] considered the problem of weighting Sun influences on temperatures, here in terms of solar radiation flux. They applied Granger causality for several in-sample tests with different periods, also adopting a moving window approach. The final results showed that the influence of solar activity on the Earth’s climate varies widely over time, but a sensible influence is detectable in the second half of the 20th century, even if it seems to decrease at the end of this period, since the 80s. Another period of a significant, but weaker, influence of solar flux variations on global surface temperature has been recognized to be 1896-1939.
In a recent study, Kodra et al. [23] introduced an alternative test of causality which evidenced that the strength of linear causality from CO2 to global temperature is stronger than that in the opposite direction. They also performed a forecasting test, considering ten outof-sample observations, AR and VAR models, that confirmed the previous in-sample results.
Attanasio [24] faced the problem of testing Granger causality from CO2 radiative forcing (RF) to temperatures, using the same Toda-Yamamoto technique applied by Triacca [19]. Here, however, the deterministic component of the model was characterized only by a constant term (vs. the linear trend used by Triacca). Furthermore, several time windows were explored, by expanding them from present to past: this approach allowed the author to estimate the parameters of the model by considering always the most recent observations. In this paper a clear Granger causality from CO2 RF to temperatures has been recognized since 1850. Replacing this anthropogenic forcing with natural forcings led to discover no Grangercausal link with temperatures.
More recently, Triacca et al. [25] extended the work by Attanasio [24] by considering several trivariate systems with the presence of a context variable–a natural forcing or an index of natural variability. Their results show that the Granger causal link between the radiative forcing of greenhouse gases and global temperature persists even in these cases, so reflecting its robustness.
This review of in-sample studies shows that several different approaches have been performed for application of Granger causality tests and that the corresponding results are sometimes contrasting.
Obviously, not all these studies used the same regressive models. Furthermore, some pioneering research was based on the use of variables that, probably, are not directly influencing temperatures, as one should require for the application of a linear method. At present, for instance, the direct influence of greenhouse gases is generally described by their radiative forcings, rather than by their concentrations or, even, their emissions, as done in [16]. Finally, in other studies [17] Granger causality has been applied in a multivariate framework where a problem of dimensionality clearly rises: they had too many free parameters in the models if compared with the time series length, so that the efficiency of the estimate parameters is not assured and overfitting becomes more probable.
However, it seems to us that even other problems affect the in-sample approach and this fact can weaken the robustness of the results obtained in this framework. In what follows we briefly discuss this situation.
First of all, before performing in-sample tests for Granger causality, it is important to establish the stochastic properties of the time series involved, by analyzing whether these series are stationary, non-stationary or cointegrated, because, for instance, the use of non-stationary time series can lead to spurious causality results [26-28]. Of course, the weakness of this approach is that incorrect conclusions drawn by this preliminary analysis may affect the results of causality tests and their reliability.
A way to overcome this situation can be the use of the Toda-Yamamoto technique [20], that is robust to the integration and possible co-integration properties of the variables. In fact, one can apply it whether the variables are stationary, integrated or co-integrated of an arbitrary order: this procedure requires only the knowledge of the maximum order of integration of the series. On the other hand, due to the further delays introduced, this technique emphasizes the problem of overfitting.
As a matter of fact, significant in-sample Granger causality does not guarantee significant out-of-sample predictability. Out-of-sample tests are often recommended because they are able to catch the true forecasting ability of one variable for another, and the results are more robust in terms of overfitting [29-31].
In order to overcome these problems, according to the analysis of Ashley et al. [32], in recent papers [33,34] we used a technique that relies on the out-of-sample comparison of the forecasting performance of two linear models. This may be more robust in terms of model selection biases and overfitting [30,31]. Furthermore, according to Granger’s definition, Granger causality builds upon the notion of incremental predictability, so that our out-of-sample approach is more keeping the spirit of the original definition by Granger [6]. In the next section a review of this approach will be presented.
5. Out-of-Sample Granger Analyses for Climatic Attribution
In this section, we will briefly sketch the method used and the results obtained in two studies recently published [33,34]. For further details, the reader may refer directly to these papers.
The final aim of the first paper [33] was to establish which external forcings can be considered Granger causal for global temperature. We analyzed the influence of many natural and anthropogenic forcings in a bivariate manner.
Total solar irradiance (TSI) describes quite well the direct effect of Sun on Earth’s climate in terms of radiative forcing; cosmic ray intensity (CRI) can be considered as an indirect effect of our star (by means of solar wind) on some processes of climatic interest, such as the formation of clouds; stratospheric aerosol optical thickness (SAOT) summarizes the impact of strong volcanic eruptions and their interference with climate due to the emission and persistence in the low stratosphere of volcanic ash composed by sulfates. All these forcings can be considered as natural.
As far as anthropogenic forcings are concerned, CO2, CH4 and N2O concentrations data were taken into account for these major greenhouse gases (GHG), their single radiative forcings (RF) were calculated and considered as effective forcings, and also a GHG-total RF has been estimated.
By taking all these data into account, we were able to test the influence of a wide range of forcings on global temperature, even of forcings never considered before in causality analyses but at present very discussed in the arena of the climate debate, such as CRI, whose role is very controversial.
If we consider 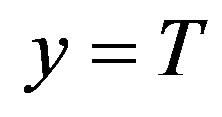 and
and 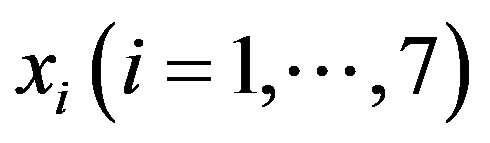 = one of the external forcings, in our application we compared the predictive ability one step ahead (in terms of mean square errors—MSE) of the two following nested regression models:
= one of the external forcings, in our application we compared the predictive ability one step ahead (in terms of mean square errors—MSE) of the two following nested regression models:
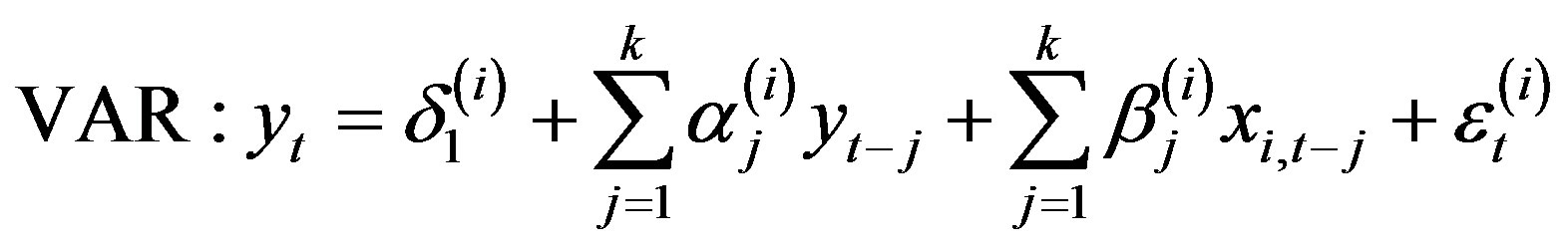 (2)
(2)
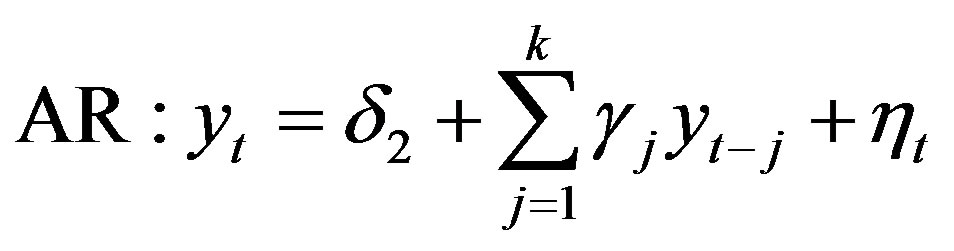 (3)
(3)
Here, 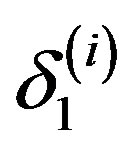 and
and 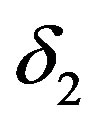 are constants included as deterministic terms,
are constants included as deterministic terms, 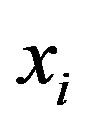 is the i-th forcing,
is the i-th forcing, 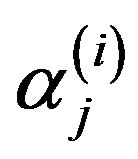 ,
, 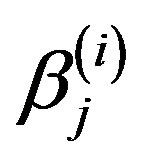 and
and  are coefficients of our regressions,
are coefficients of our regressions, 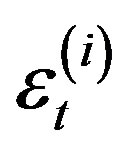 and
and 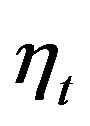 are univariate white noises. The order k of the models was kept low
are univariate white noises. The order k of the models was kept low , so that the models are parsimonious and the residuals are uncorrelated, and the models finally selected were those endowed with the best predictive performance on each test set.
, so that the models are parsimonious and the residuals are uncorrelated, and the models finally selected were those endowed with the best predictive performance on each test set.
The Granger out-of-sample tests were performed on five test sets which span the following periods: 1941- 2007, 1951-2007, 1961-2007, 1971-2007, 1981-2007. For each test set, the correspondent training set is composed by data patterns since 1850 till the year before the beginning of the test set itself.
Fixed and recursive schemes were adopted for predicttions. Under the recursive scheme we used the training set for the first estimate and forecast out of sample one-step ahead; then we added an annual pattern to our training set, obtained a second estimate and forecast for the next year; and so on, iteratively. Under the fixed scheme the parameters were estimated only once on the original training set and every one-step ahead forecast has been obtained using just these fixed parameters.
The statistical significance of results has been evaluated by MSE-t and MSE-REG tests, as described in [35]. However, we were not able to use critical values of these test statistics, as reported in [35], because our series are not stationary. So, we performed a bootstrap procedure to calculate our critical values: see [33] for further details.
The results obtained by this out-of-sample Granger analysis are very clear. If we take TSI, CRI or SAOT as x variable, in every case (any natural forcing, scheme and test set considered) the null hypothesis of non-Granger causality on 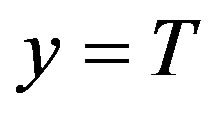 is never rejected (with only two exceptions), even just at 10% significance level. Vice versa, there is a clear general evidence of Granger causality from anthropogenic forcings to global temperature (see [33] for the complete results and other detailed considerations).
is never rejected (with only two exceptions), even just at 10% significance level. Vice versa, there is a clear general evidence of Granger causality from anthropogenic forcings to global temperature (see [33] for the complete results and other detailed considerations).
In short, this paper shows that a genuine Granger out-of-sample predictive approach permits to overcome problems and contrasting results shown by previous insample analyses and gives a clear contribution to the assessment of temperature attribution.
In the paper just discussed we limited our analysis to a bivariate framework. However, it is well known that Granger causal links are sensitive to the information set which is employed in the analysis. Changing the information set, by extending or reducing the number of time series in the study, may lead to different Granger causal links. In particular, it is possible to find Granger causality from x to y in a bivariate system although x does not Granger cause y when also the information contained in a third variable z is taken into account [36,37].
Furthermore, together with this technical note about the possible role of omitted variables on results coming from Granger causality analyses, also a more climatic argument must be taken into account, which leads to possibly extend the information set considered here. In [33] we considered the influence of external forcings in VAR forecast improvements with respect to the predictions of the AR model built on data about T only. But, as a matter of fact, the climate system shows its own internal variability which can contribute to changes in global temperature, at least at decadal scale. Thus, it seems a good idea to insert some index of this climate variability as a context variable z in the information set: this has been done in [34].
The scope of this new paper was to investigate the causal influence of natural and anthropogenic forcings in a trivariate framework, where z is represented by one of the following indices: Southern Oscillation Index (SOI), related to El Niño Southern Oscillation (ENSO); Pacific Decadal Oscillation (PDO); Atlantic Multidecadal Oscillation (AMO).
We considered the VAR unrestricted model described in Equation (1) and the following restricted model:
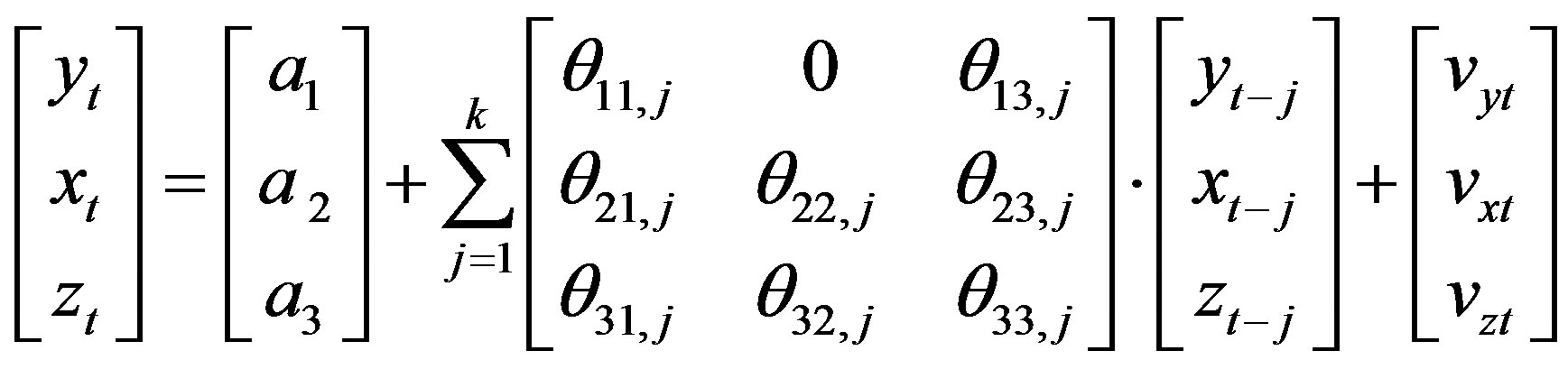 . (4)
. (4)
By adopting the same test sets as in the previous paper, the one-step-ahead forecast errors were calculated as:
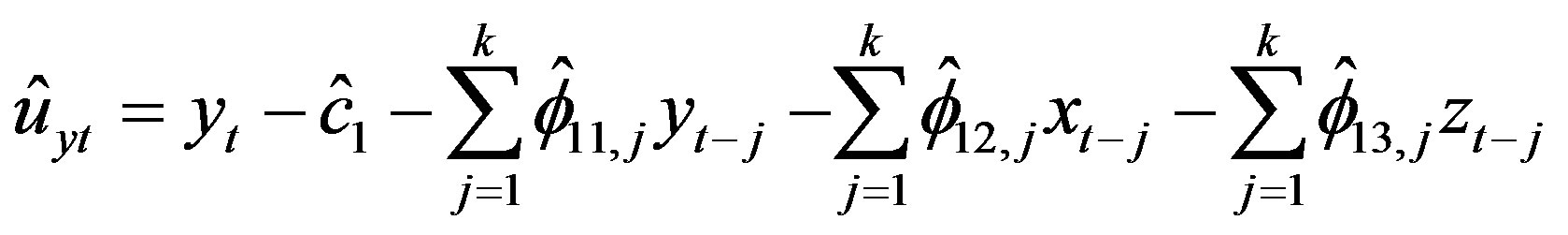 , (5)
, (5)
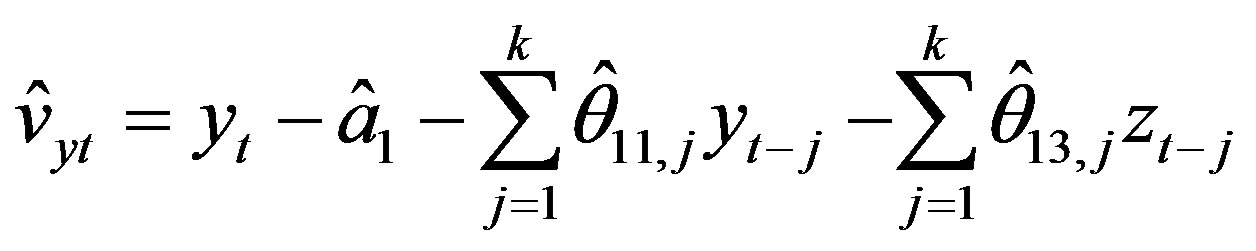 . (6)
. (6)
Then we evaluated the MSE of these predictions and used the MSE-t and MSE-REG tests in order to test the null hypothesis. As in the previous paper, a bootstrap procedure has been performed to calculate the critical values of these tests (see [34] for further details).
The results of this paper can be summarized as follows. If we take GHG-total RF as the x variable, in every case (all circulation patterns and test sets considered)—except one—the null hypothesis of Granger non-causality on T is rejected at the 5% significance level, and very often also at 1% significance. This is clear evidence that there is a causal link (in the Granger sense) between GHG-total RF and global temperature since 1941 up to the present day.
On the other hand, if TSI is considered as the x variable, a Granger causal link is significant only in the first test set when AMO is included in the information set, and in the first two sets when PDO and ENSO are considered. In more recent periods this causal link disappears.
The situation becomes even clearer if the p-values of tests are plotted for every test period, as in Figure 1: see [34] for other figures and detailed tables. Here, it is evident that, while the influence of GHG-total RF on global temperature remains important throughout all the periods, the Granger causal link between TSI and T becomes progressively less marked with time and completely disappears for the last two periods. In particular, the influences of GHG-total RF and TSI on T appear comparable till the 50s, but, after that decade, a clear causal decoupling be-
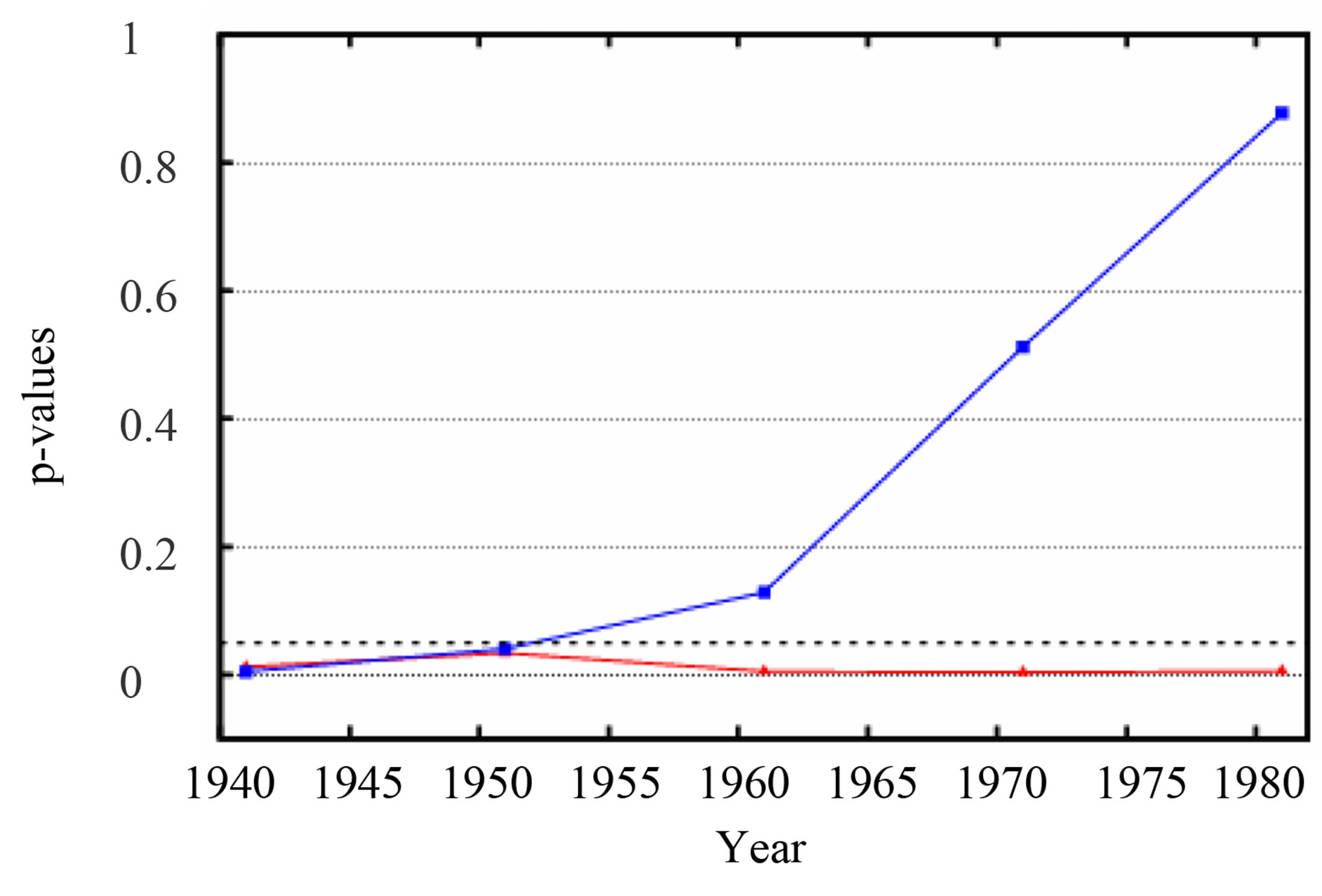
Figure 1. Plot of the p-values from the MSE-REG test when x = TSI (blue line) and x = GHG-total RF (red line) for z = ENSO. The significance threshold of 0.05 is shown (dashed line). The increase in p-values over the recent decades is evident for the performance of the model with TSI.
tween TSI and T is evident and very marked in the data of our Granger analysis. At the same time, the Granger causality from GHG-total RF to T remains robust and, possibly, becomes even more evident: the p-values, which are already very small, decrease further.
In particular, in this way we evidenced a causal decoupling between Sun and global temperatures which has been pictured previously just in terms of simple correlations and graphical methods [38,39].
6. Conclusions, Discussion and Prospects
As shown in previous sections, a number of attempts have been performed at applying the concept of Granger causality to climatic problems and, more specifically, to climatic attribution. After some pioneering works, where the choice of influencing variables is quite dubious or the dimensionality of the multivariate models probably exceeds the maximum number of parameters for obtaining reliable results, at present the application of Granger causality to the climate framework is quite well posed.
Nevertheless, our review and discussion at Section 4 show that in-sample approaches may crucially depend on preliminary analyses of the stochastic properties of time series involved: this could explain also the somewhat contrasting results obtained by these attribution studies.
Therefore, in order to overcome this critical situation, we performed out-of-sample Granger analyses for the attribution of recent global warming. This approach is less dependent on the preliminary assumptions, and more properly predictive, and more in the spirit of the original concept of Granger causality. The results obtained in this way are very clear: the radiative forcings of greenhouse gases appear as the main temperature drivers, while natural forcings do not Granger cause T in the last decades, in the case of Sun even if the principal patterns of climate variability are considered in an extended trivariate model. Furthermore, the direct Sun influence on T (via total solar irradiance) shows a recent causal decoupling since the 60s.
Obviously, even if these results represent a clear contribution to the problem of attribution of recent global warming, a discussion of methods and outcomes can show directions of future work. We briefly do this in what follows.
The first open problem is surely to test the robustness of these results when extended information sets are considered. Probably, due to the problem of dimensionality, this can be done effectively just in a trivariate framework. Here, anyway, it is possible to study several combinations of variables considered as x (the variable to be tested for Granger causality) and z (the context variable). Furthermore, in this framework, analyses about the rising of spurious or indirect causalities can be performed.
As a specific study inside a trivariate context, an interesting analysis can be also performed about the joint roles of direct and indirect Sun influences on T, where the direct forcing could be represented by solar irradiance and the indirect one by cosmic rays (modulated by solar wind).
In our opinion, however, a more basic problem concerns the application of a linear technique to studies of causation in a nonlinear system such as climate. In the majority of studies reviewed here, the variables used are averaged in space (the entire world) and time (one year). Thus, it is quite reasonable that, as a consequence of the central limit theorem [40], averaging can produce nearlinear climate relations among variables of the climate system, even if we have to do with highly nonlinear relations at shorter space-time scales. In this context Granger causality may be applied with a good confidence; but what happens if the averaging is performed on reduced space-time scales?
With the final aim at approaching this general problem, Attanasio and Triacca [41] developed a nonlinear extension of a Granger causality model based on neural networks and applied it to the classical problem of CO2 influences on T. Outcomes from this nonlinear Granger causality analysis are consistent with other results assessing that CO2 radiative forcing causes recent global temperatures.
Even if the analysis of this research exceeds the scope of this paper, in our opinion this approach could show its usefulness and should be considered in analyses of attribution at reduced space-time scales and when the behavior of other variables of climatic importance, such as precipitation, are considered. It is well known, in fact, that many nonlinear processes are involved in the hydrological cycle and they cannot be easily “averaged away”.
We hope to have shown that the research in this field is quite active and that future exciting studies can be surely envisaged.
7. Acknowledgements
We thank I. M. Hedgecock for useful hints.
REFERENCES
- A. Pasini, “From Observations to Simulations. A Conceptual Introduction to Weather and Climate Modeling,” World Scientific, Singapore City, 2005.
- G. C. Hegerl, et al., “Understanding and Attributing Climate Change,” In: S. Solomon, et al., Eds., Climate Change 2007: The Physical Science Basis, Cambridge University Press, Cambridge, 2007, pp. 663-745.
- A. Pasini, M. Lorè and F. Ameli, “Neural Network Modelling for the Analysis of Forcings/Temperatures Relationships at Different Scales in the Climate System,” Ecological Modelling, Vol. 191, No. 1, 2006, pp. 58-67. http://dx.doi.org/10.1016/j.ecolmodel.2005.08.012
- A. Pasini and R. Langone, “Attribution of Precipitation Changes on a Regional Scale by Neural Network Modeling: A Case Study,” Water, Vol. 2, No. 3, 2010, pp. 321-332. http://dx.doi.org/10.3390/w2030321
- A. Pasini and R. Langone, “Influence of Circulation Patterns on Temperature Behavior at the Regional Scale: A Case Study Investigated via Neural Network Modeling,” Journal of Climate, Vol. 25, No. 6, 2012, pp. 2123-2128. http://dx.doi.org/10.1175/JCLI-D-11-00551.1
- C. W. J. Granger, “Investigating Causal Relations by Econometric Models and Cross-Spectral Methods,” Econometrica, Vol. 37, No. 3, 1969, pp. 424-438. http://dx.doi.org/10.2307/1912791
- C. Diks and M. Mudelsee, “Redundancies in the Earth’s Climatological Time Series,” Physics Letters A, Vol. 275, No. 5-6, 2000, pp. 407-414. http://dx.doi.org/10.1016/S0375-9601(00)00613-7
- R. K. Kaufmann, L. Zhou, R. B. Myneni, C. J. Tucker, D. Slayback, N. V. Shabanov and J. Pinzon, “The Effect of Vegetation on Surface Temperature: A Statistical Analysis of NDVI and Climate Data,” Geophysical Research Letters, Vol. 30, No. 22, 2003, p. 2147. http://dx.doi.org/10.1029/2003GL018251
- J. B. Elsner, “Evidence in Support of the Climate Change —Atlantic Hurricane Hypothesis,” Geophysical Research Letters, Vol. 33, No. 16, 2006, Article ID: L16705. http://dx.doi.org/10.1029/2006GL026869
- J. B. Elsner, “Granger Causality and Atlantic Hurricanes,” Tellus A, Vol. 59, No. 4, 2007, pp. 476-485. http://dx.doi.org/10.1111/j.1600-0870.2007.00244.x
- T. J. Mosedale, D. B. Stephenson, M. Collins and T. C. Mills, “Granger Causality of Coupled Climate Processes: Ocean Feedback on the North Atlantic Oscillation,” Journal of Climate, Vol. 19, No. 7, 2006, pp. 1182-1194. http://dx.doi.org/10.1175/JCLI3653.1
- R. K. Kaufmann, K. C. Seto, A. Schneider, Z. Liu, L. Zhou and W. Wang, “Climate Response to Rapid Urban Growth: Evidence of a Human-Induced Precipitation Deficit,” Journal of Climate, Vol. 20, No. 10, 2007, pp. 2299-2306. http://dx.doi.org/10.1175/JCLI4109.1
- I. I. Mohkov, D. A. Smirnov, P. I. Nakonechny, S. S. Kozlenko, E. P. Seleznev and J. Kurths, “Alternating Mutual Influence of El Niño/Southern Oscillation and Indian Monsoon,” Geophysical Research Letters, Vol. 38, 2011, Article ID: L00F04.
- R. S. J. Tol and A. F. de Vos, “Greenhouse Statistics— Time Series Analysis,” Theoretical and Applied Climatology, Vol. 48, No. 2-3, 1993, pp. 63-74. http://dx.doi.org/10.1007/BF00864914
- R. S. J. Tol and A. F. de Vos, “A Bayesian Statistical Analysis of the Enhanced Greenhouse Effect,” Climatic Change, Vol. 38, No. 1, 1998, pp. 87-112. http://dx.doi.org/10.1023/A:1005390515242
- L. Sun and M. Wang, “Global Warming and Global Dioxide Emission: An Empirical Study,” Journal of Environmental Management, Vol. 46, No. 4, 1996, pp. 327- 343. http://dx.doi.org/10.1006/jema.1996.0025
- R. K. Kaufmann and D. I. Stern, “Evidence for Human Influence on Climate from Hemispheric Temperature Relations,” Nature, Vol. 388, No. 6637, 1997, pp. 39-44. http://dx.doi.org/10.1038/40332
- U. Triacca, “On the Use of Granger Causality to Investigate the Human Influence on Climate,” Theoretical and Applied Climatology, Vol. 69, No. 3-4, 2001, pp. 137-138. http://dx.doi.org/10.1007/s007040170019
- U. Triacca, “Is Granger Causality Analysis Appropriate to Investigate the Relationship between Atmospheric Concentration of Carbon Dioxide and Global Surface Air Temperature?” Theoretical and Applied Climatology, Vol. 81, No. 3-4, 2005, pp. 133-135. http://dx.doi.org/10.1007/s00704-004-0112-1
- H. Y. Toda and T. Yamamoto, “Statistical Inference in Vector Autoregression with Possibly Integrated Processes,” Journal of Econometrics, Vol. 66, No. 1-2, 1995, pp. 225-250. http://dx.doi.org/10.1016/0304-4076(94)01616-8
- R. Reichel, P. Thejll and K. Lassen, “The Cause-andEffect Relationship of Solar Cycle Length and the Northern Hemisphere Air Surface Temperature,” Journal of Geophysical Research, Vol. 106, No. A8, 2001, pp. 15635- 15641. http://dx.doi.org/10.1029/2001JA900027
- I. I. Mohkov and D. A. Smirnov, “Diagnostics of CauseEffect Relation between Solar Activity and the Earth’s Global Surface Temperature,” Izvestiya, Atmospheric and Oceanic Physics, Vol. 44, No. 3, 2008, pp. 263-272. http://dx.doi.org/10.1134/S0001433808030018
- E. Kodra, S. Chatterjee and A. R. Ganguly, “Exploring Granger Causality between Global Average Observed Time Series of Carbon Dioxide and Temperature,” Theoretical and Applied Climatology, Vol. 104, No. 3-4, 2011, pp. 325-335. http://dx.doi.org/10.1007/s00704-010-0342-3
- A. Attanasio, “Testing for Linear Granger Causality from Natural/Anthropogenic Forcings to Global Temperature Anomalies,” Theoretical and Applied Climatology, Vol. 110, No. 1-2, 2012, pp. 281-289. http://dx.doi.org/10.1007/s00704-012-0634-x
- U. Triacca, A. Attanasio and A. Pasini, “Anthropogenic Global Warming Hypothesis: Testing Its Robustness by Granger Causality Analysis,” Environmetrics, Vol. 24, No. 4, 2013, pp. 260-268. http://dx.doi.org/10.1002/env.2210
- J. Y. Park and P. C. B. Phillips, “Statistical Inference in Regressions with Integrated Processes: Part 2,” Economic Theory, Vol. 5, No. 1, 1989, pp. 95-131. http://dx.doi.org/10.1017/S0266466600012287
- J. H. Stock and M. W. Watson, “Interpreting the Evidence on Money-Income Causality,” Journal of Econometrics, Vol. 40, No. 1, 1989, pp. 161-181. http://dx.doi.org/10.1016/0304-4076(89)90035-3
- C. A. Sims, J. H. Stock and M. W. Watson, “Inference in Linear Time Series Models with Some Unit Roots,” Econometrica, Vol. 58, No. 1, 1990, pp. 113-144. http://dx.doi.org/10.2307/2938337
- J. Chao, V. Corradi and N. Swanson, “Out-of-Sample Test for Granger Causality,” Macroeconomic Dynamics, Vol. 5, 2001, pp. 598-620.
- T. Clark, “Can Out-of-Sample Forecast Comparisons Help Prevent Overfitting?” Journal of Forecasting, Vol. 23, No. 2, 2004, pp. 115-139. http://dx.doi.org/10.1002/for.904
- S. Gelper and C. Croux, “Multivariate Out-of-Sample Tests for Granger Causality,” Computational and Statistical Data Analysis, Vol. 51, No. 7, 2007, pp. 3319-3329. http://dx.doi.org/10.1016/j.csda.2006.09.021
- R. Ashley, C. W. J. Granger and R. Schmalansee, “Advertising and Aggregate Consumption: An Analysis of Causality,” Econometrica, Vol. 48, No. 5, 1980, pp. 1149- 1167. http://dx.doi.org/10.2307/1912176
- A. Attanasio, A. Pasini and U. Triacca, “A Contribution to Attribution of Recent Global Warming by Out-ofSample Granger Causality Analysis,” Atmospheric Science Letters, Vol. 13, No. 1, 2012, pp. 67-72. http://dx.doi.org/10.1002/asl.365
- A. Pasini, U. Triacca and A. Attanasio, “Evidence of Recent Causal Decoupling between Solar Radiation and Global Temperature,” Environmental Research Letters, Vol. 7, No. 3, 2012, Article ID: 034020. http://dx.doi.org/10.1088/1748-9326/7/3/034020
- M. W. McCracken, “Asymptotics for Out-of-Sample Tests of Granger Causality,” Journal of Econometrics, Vol. 140, No. 2, 2007, pp. 719-752. http://dx.doi.org/10.1016/j.jeconom.2006.07.020
- H. Lütkepohl, “Non-Causality Due to Omitted Variables,” Journal of Econometrics, Vol. 19, No. 2-3, 1982, pp. 367-378. http://dx.doi.org/10.1016/0304-4076(82)90011-2
- J. D. Hamilton, “Time Series Analysis,” Princeton University Press, Princeton, 1994.
- M. Lockwood and C. Fröhlich, “Recent Oppositely Directed Trends in Solar Climate Forcings and the Global Mean Surface Air Temperature,” Proceedings of the Royal Society A, Vol. 463, No. 2086, 2007, pp. 2447-2460. http://dx.doi.org/10.1098/rspa.2007.1880
- P. Stauning, “Solar Activity-Climate Relations: A Different Approach,” Journal of Atmospheric and Solar-Terrestrial Physics, Vol. 73, No. 13, 2011, pp. 1999-2012. http://dx.doi.org/10.1016/j.jastp.2011.06.011
- A. Yuval and W. W. Hsieh, “The Impact of Time-Averaging on the Detectability of Nonlinear Empirical Relations,” Quarterly Journal of the Royal Meteorological Society, Vol. 128, 2002, pp. 1609-1622. http://dx.doi.org/10.1256/00359000260247381
- A. Attanasio and U. Triacca, “Detecting Human Influence on Climate Using Neural Networks Based Granger Causality,” Theoretical and Applied Climatology, Vol. 103, No. 1-2, 2011, pp. 103-107. http://dx.doi.org/10.1007/s00704-010-0285-8
NOTES
*Corresponding author.

