International Journal of Astronomy and Astrophysics
Vol.04 No.04(2014), Article ID:52772,15 pages
10.4236/ijaa.2014.44062
A Solution of Kepler’s Equation
John N. Tokis
Technological Educational Institute of Epirus, Ioannina, Greece
Email: JohnTokis@ioa.teiep.gr
Academic Editor: Ran Zhou, Theoretical High Energy Physics Group, Fermi National Accelerator Laboratory, China
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 October 2014; revised 24 November 2014; accepted 22 December 2014
ABSTRACT
The present study deals with a traditional physical problem: the solution of the Kepler’s equation for all conics (ellipse, hyperbola or parabola). Solution of the universal Kepler’s equation in closed form is obtained with the help of the two-dimensional Laplace technique, expressing the universal functions as a function of the universal anomaly and the time. Combining these new expressions of the universal functions and their identities, we establish one biquadratic equation for universal anomaly
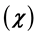 for all conics; solving this new equation, we have a new exact solution of the pre- sent problem for the universal anomaly as a function of the time. The verifying of the universal Kepler’s equation and the traditional forms of Kepler’s equation from this new solution are discussed. The plots of the elliptic, hyperbolic or parabolic Keplerian orbits are also given, using this new solution.
for all conics; solving this new equation, we have a new exact solution of the pre- sent problem for the universal anomaly as a function of the time. The verifying of the universal Kepler’s equation and the traditional forms of Kepler’s equation from this new solution are discussed. The plots of the elliptic, hyperbolic or parabolic Keplerian orbits are also given, using this new solution.
Keywords:
Keplerian Motion, Universal Kepler’s Equation, Universal Anomaly, Two-Dimensional Laplace Transforms

1. Introduction
In the Keplerian problem, a body of mass
 follows a conic orbit, for which the focus is identified to the center of attracting body (with mass
follows a conic orbit, for which the focus is identified to the center of attracting body (with mass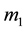 ). The Keplerian motion is described by the fundamental differential equation of the physical two-body problem:
). The Keplerian motion is described by the fundamental differential equation of the physical two-body problem:
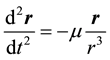 (1)
(1)
where
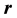 is the vector position of the moving body related to the attraction center and
is the vector position of the moving body related to the attraction center and
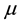 the gravitational parameter defined by
the gravitational parameter defined by
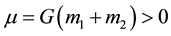 (where
(where
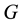 the Newtonian gravitational constant) (see [1] , Equation (6.2.3)).
the Newtonian gravitational constant) (see [1] , Equation (6.2.3)).
The traditional form of Kepler’s equation, which can be obtained directly from Equation (1) (see [1] , Section 6.3 and [2] ), is normally written as:
For elliptic orbits
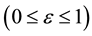
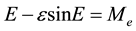 (2a)
(2a)
for hyperbolic orbits
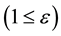
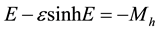 (2b)
(2b)
where
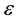 is the eccentricity,
is the eccentricity,
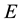 the eccentric anomaly and
the eccentric anomaly and
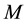 the mean anomaly, which is defined as
the mean anomaly, which is defined as
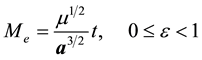 (2c)
(2c)


(see [2] , Equation (11) and [3] , Equations (4.35) and (4.51)). Remark that the time






Johannes Kepler announced the relevant laws of above equation early in 1609 and 1619 [4] . He has used physics as a guide in this discovery [5] . For four centuries, the Kepler’s problem is to solve the nonlinear Kepler’s Equation (2) for the eccentric anomaly.
Early analytical solution of Kepler’s equation was considered in a comprehensive study of Tisserand [6] . Recently, analytical works of the solution and use of Kepler’s equation have been proposed by various authors (see, e.g., [7] - [12] ).
In virtually every decade from 1650 to the present, there have appeared papers devoted to the solution of this Kepler’s equation. Its exact analytical solution is unknown, and therefore, efficient procedures to solve it numerically have been well discussed in many standard text books of Celestial Mechanics and Astrodynamics as well as in a large number of papers. Colwell [13] contains extensive references to the Kepler problem in his book. During last two decades, studies were carried out by several investigators of the present problem [2] [14] -[18] . In these studies, they used numerical or approximations methods for solution of the Kepler’s equation. Hence, it appears that an analytical solution of the Kepler’s equation will be of great interest.
In the current study, an analytical investigation of the Kepler’s equation real roots in closed form is presented. In Section 2, we will establish the general form of Kepler’s equation and will clear up the useful identities of the universal functions. In Section 3, using the two-dimensional Laplace transform technique, we will present an analytical solution for the universal Kepler’s equation, obtaining the universal functions





Finally, discussion of the results, thus obtained, is presented in Section 5; the new solution of the problem will prove that verifies the traditional form of Kepler’s equations for elliptic, hyperbolic or parabolic orbits. The elliptic, hyperbolic or parabolic Keplerian motion is easily plotted, using this new solution.
2. General Form of Kepler’s Equation
In order to solve the Kepler’s Equation (2), we use here the generalized form of this equation with the universal functions and the universal anomaly instead of the eccentric anomaly (see [3] , Section 4.5).
Working for the Kepler’s Equation (2), we consider an object following a path of same eccentricity














(see [3] , Equation (4.71)) and related to the classical eccentric anomaly by



where E is the eccentric anomaly angle of elliptic or hyperbolic orbit and D the parabolic eccentric anomaly of parabolic orbit with dimension




Depending on the sign of










From the initial condition






where



Remark that the


Now, using the universal functions defined by

with their following useful properties:




(see [3] , Equation (9.73)), the two forms of Kepler’s Equation (2) are incorporated in one universal equation

which is a standard form of the traditional Kepler’s Equations (2) with the epoch at pericenter passage (see [9] , Equation (23) and [2] , Equation (29)). The general formula (10) is valid for all values of



To find out the expression of many orbital quantities, e.g. the magnitude of the position vector

3. Solution of the Universal Kepler’s Equation
In order to obtain the analytical solution of the present problem, we shall solve first the universal Kepler’s equation Equation (10), obtaining the universal functions

The universal functions




(see Equations (9)) and the universal Kepler’s Equation (10) becomes

From the initial condition



The application of double Laplace transform (with respect to




where




Now, the universal function


where we have abbreviated

with dimensions:
The universal functions




(see Equations (9c)) and the universal Kepler’s Equation (10) becomes

For



Similarly as in the case of




(cf., Appendix). Inverting


where we have defined the non-dimensional function

Then, substituting the results of Equation (14) and (19) into the relations






where


4. Analytical Solution of the Problem
In order to obtain a solution for the universal anomaly


where




Substituting Equation (24) (with


To find out two more relations between






Further, we can find one more relation using the basic identity


The three Equations (25), (26) and (27) are a system of the three unknowns:




Finally, substituting Equations (28) into Equation (27), we obtain the following biquadratic equation for universal anomaly

where we have abbreviated



with dimensions:


The solution of the biquadratic Equation (29) gives the relation between the universal anomaly


Solving the new biquadratic Equation (29), we get the solution of the present problem for the universal anomaly



where we have abbreviated

particularly, for elliptic orbits


for hyperbolic orbits

and for parabolic orbits

Remark that the discriminant of the biquadratic Equation (29) is




where


In the case of parabolic orbits where the limiting case







The Equation (31) is the solution of the present problem for all conics (ellipse, hyperbola or parabola) and expresses the relation between the universal anomaly

Knowing the solution of the universal anomaly





Then, the universal functions (19), (14), (21) and (22) are expressed as functions of the time t as show below




The magnitude of the position vector


(see [3] , Equation (4.82) and [14] , Equation (8)). Substituting into Equation (36b) the new expressions of


Furthermore, if we work in the orbital reference system with the origin at the attracting center (or focus), we chose the










where








where


5. Discussion
Using the standard form of the universal Kepler’s equation (10) with the epoch at pericenter passage, we have derived a new biquadratic equation (29) for universal anomaly




The new solution (31) of the present problem was obtained solving Equation (29) with initial-value conditions for the orbiting body at time




The solution (31) is a solution of the present problem. Indeed, the new expressions of the universal functions

The solution (31) verifies also the traditional forms of Kepler’s Equation (2). Particularly, in the case of elliptic orbits


where


Note that



Similarly, in the case of hyperbolic orbits


where


Finally, in the case of parabolic orbits


From the other hand, the standard and hyperbolic trigonometric functions of Equations (2) are expressed as


where we have use Equation (35) and the relationship between the function U1 and the standard and hyperbolic
trigonometric functions of Equations (2):


and hyperbola, respectively (see [3] , Problem 4 - 21 and [9] , Equation (24)).
Now, we will prove that the Equations (40) and (42) represent the solutions of the traditional forms of Kepler’s Equations (2). Indeed, it can be shown that the left-hand sides of Equations (2) are reduced to the right- hand sides, namely


in accordance with the Equations (40), (42) and (45).
It should be pointed out that our solutions for eccentric anomaly (cf., Equations (40) and (42)) are ready for physical applications in the corresponding Keplerian orbits.
In addition to above Keplerian orbits, the new solution (33b) of the present problem for the case of parabola (


Remark that the parabolic Keplerian equation is called Barker’s equation (see [3] , Equation (4.24)). Indeed, from the definition (8) for the universal functions we have



where


In order to study the Keplerian orbits with the help of the new solutions, we use also the cartesian coordinates











where we have defined the non-dimensional relation

in accordance to the Equations (39). Then, we introduce the non-dimensional coordinates


The new expressions (52) verify the following equations of ellipse




where


In the other hand, for the case of parabola




Then, we have, from Equations (54),

The last Equation (55) is the equation of parabola, which passes through its pericenter with coordinates
(see [3] , Equation (3.22)). The non-dimensional form of Equation (55) is

with the non-dimensional coordinates

In addition to above results for the non-dimensional coordinates we have (for physical application) the corresponding expressions:
For elliptic orbits


for hyperbolic orbits


for parabolic orbits


where







In order to get a physical insight into the new solution of the Kepler’s problem, we apply the above results for the system Earth-Moon. For this system the eccentricity of the Moon is






Note that the use of the upper limit of the mean anomaly, given from the relation






Figure 1. The elliptic orbit of the Moon

Figure 2. Two elliptic Keplerian orbits with eccentricities


eccentricity





Now, varying the mean anomaly



with the eccentricity


Finally, varying the mean anomaly




6. Conclusions
This work presents a solution to the well known Keplerian two body physical problem. From the investigation
Figure 3. The hyperbola of an orbiting body (with

Figure 4. The parabola of an orbiting body (with

for this new solution, the main conclusions have been drawn as following:
1) An analytical solution for the universal Kepler’s equation has been determined, obtaining the universal functions


2) Using an explicit expression for the universal anomaly



3) The solution

4) This new analytical solution for the universal anomaly has been discussed and proved that verifies the universal Kepler’s equation (cf., Equation (10)), since the time depended universal functions U3 and U1 verify this equation. Then, the solutions for the eccentric anomaly (cf., Equations (40) and (42)) were also proved that verify the traditional form of Kepler’s equations for elliptic or hyperbolic orbits. This new solution for the universal anomaly has also proved that verifies the traditional Barker’s equation for parabolic orbits [11] . The elliptic, hyperbolic or parabolic Keplerian motion is plotted, using this analytical solution.
5) To our knowledge, this work gives in closed form the actual analytical solution of the Kepler’s problem. The advantage of the new solution is simple and ready for physical applications in the elliptic, hyperbolic or parabolic Keplerian orbits.
References
- Dandy, J.M.A. (2003) Fundamentals of Celestial Mechanics. 2nd Edition, Willmann-Bell, Virginia.
- Fukushima, T. (1999) Fast Procedure Solving Universal Kepler’s Equation. Celestial Mechanics and Dynamical As- tronomy, 75, 201-226. http://dx.doi.org/10.1023/A:1008368820433
- Battin, R.H. (1999) An Introduction to the Mathematics and Methods Astrodynamics. Revised Edition, AIAA Educa- tion Series, New York. http://dx.doi.org/10.2514/4.861543
- Voelkel, J.R. (2001) The Composition of Kepler’s Astronomia Nova. Princeton University Press, New York. http://press.princeton.edu/titles/7187.html
- Bruce, S. (1987) Kepler’s Physical Astronomy. Springer-Verlag, New York.
- Tisserand, F. (1894) Mécanique Céleste. Vol. 3. Gauthier-Villars, Paris.
- Siewert, C.E. and Burniston, E.E. (1972) An Exact Analytical Solution of Kepler’s Equation. Celestial Mechanics, 6, 294-304. http://link.springer.com/article/10.1007/BF01231473#page-1
- Tokis, J.N. (1973) Effects of Tidal Dissipative Processes on Stellar Rotation. PhD Thesis, Victoria University of Man- chester, Manchester.
- Fernandes, S.daS. (2003) Universal Closed-form of Lagrangian Multipliers for Coast-Arcs of Optimum Space Trajec- tories. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 25, 1-9. http://dx.doi.org/10.1590/S1678-58782003000400004
- Condurache, D. and Martinusi, V. (2006) Vectorial Regularization and Temporal Means in Keplerian Motion. Journal of Nonlinear Mathematical Physics (World Scientific), 13, 420-440. http://dx.doi.org/10.2991/jnmp.2006.13.3.7
- Pathan, A. and Collyer, T. (2006) A Solution to a Cubic―Barker’s Equation for Parabolic Trajectories. Mathematical Gazette, 90, 398-403.
- Boubaker, K. (2010) Analytical Initial-Guess-Free Solution to Kepler’s Transcendental Equation Using Boubaker Poly- nomials Expansion Scheme BPES. Apeiron, 17, 1-12. http://redshift.vif.com/JournalFiles/V17NO1PDF/V17N1BOU.pdf
- Colwell, P. (1993) Solving Kepler’s Equation over Three Centuries. Willmann-Bell, Richmond. http://www.willbell.com/math/mc12.htm
- Floria, L. (1996) A Proof of Universality of Arc Length as Time Parameter in Kepler Problem. Extracta Mathematicae, 11, 315-324. http://dmle.cindoc.csic.es/pdf/EXTRACTAMATHEMATICAE_1996_11_02_09.pdf
- Fukushima, T. (1998) A Fast Procedure Solving Gauss Form of Kepler’s Equation. Celestial Mechanics and Dynami- cal Astronomy, 70, 115-130. http://link.springer.com/article/10.1023%2FA%3A1026479306748#page-1
- Sharaf, M.A. and Sharaf, A.A. (1998) Closest Approach in Universal Variables. Celestial Mechanics and Dynamical Astronomy, 69, 331-346. http://link.springer.com/article/10.1023%2FA%3A1008223105130#page-1
- Sharaf, M.A. and Sharaf, A.A. (2003) Homotopy Continuation Method of Arbitrary Order of Convergence for the Two-Body Universal Initial Value Problem. Celestial Mechanics and Dynamical Astronomy, 86, 351-362. http://link.springer.com/article/10.1023/A:1024544523868#page-1
- Jia, L. (2013) Approximate Kepler’s Elliptic Orbits with the Relativistic Effects. International Journal of Astronomy and Astrophysics, 3, 29-33. http://dx.doi.org/10.4236/ijaa.2013.31004
- Aghili, A. and Salkhordeh-Moghaddam, B. (2008) Laplace Transform Pairs of N-Dimensions and Second Order Linear Partial Differential Equations with Constant Coefficients. Annales Mathematicae et Informaticae, 35, 3-10. http://www.emis.de/journals/AMI/2008/ami2008-aghili-salkhordeh.pdf
- Valkó, P.P. and Abate, J. (2005) Numerical Inversion of 2-D Laplace Transforms Applied to Fractional Diffusion Equa- tion. Applied Numerical Mathematics, 53, 73-88. http://dx.doi.org/10.1016/j.apnum.2004.10.002
- Ditkin, V.A. and Prudnicov, A.P. (1962) Operational Calculus in Two Variables and Its Application. Pergamum Press, New York.
Appendix
Solution of partial differential equations using two-dimensional Laplace transforms
The general form of second-order linear partial differential equation in two variables is given as following

where





and their one-dimensional Laplace transformations
















in accordance with the two-dimensional analysis formula, which can be written as one-dimensional analysis in the



Now, applying double Laplace transformation to both sides of Equation (A1) and using Equations (A3), we obtain the solution of Equation (A1) in the transform domain as

with the abbreviation

In order to invert this two-dimensional Laplace transform


where we keep the second transform variable


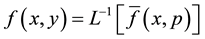 (A7)
(A7)










