International Journal of Astronomy and Astrophysics
Vol.3 No.2(2013), Article ID:32740,6 pages DOI:10.4236/ijaa.2013.32019
High Energy Emission from Magnetar Due to Giant Flare
Department of Physics, Gauhati University, Guwahati, India
Email: kader.abdul781@gmail.com
Copyright © 2013 A. Kader, K. Duorah. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 29, 2013; revised April 30, 2013; accepted May 8, 2013
Keywords: Solar Flares; Magnetic Reconnection; Gamma-Rays; Observations—Neutron Stars; Magnetic Fields—Magnetars
ABSTRACT
We propose a theoretical model for magnetar giant flare to explain the flaring activity on 2004 December 27 from SGR1806-20 comprehensively. A global rearrangement is expected by the magnetic reconnection that requires explaining the giant SGR flares. In this paper we propose two regions of flares: preflare on the surface of magnetar and main burst at a distance of light cylinder radius. Acquiring the maximum potential drop on the magnetar surface, adopting space charge limited flow model, and using magnetic field B ≈ 1015 G, the luminosities of flare energies release for the preflare phase and main burst phase are found to be in the order of 1041 erg·s−1 and 1044 erg·s−1 respectively, conforming to magnetar burst energy and flare temperature is determined by considering black body radiation.
1. Introduction
Soft gamma-ray repeaters (SGRs) and anomalous X-ray pulsars (AXPs) have been identified as isolated superstrong magnetized neutron stars—magnetars. Both SGRs and AXPs have spin periods in the range of P = 5 - 8 s. After the discovery of SGRs and AXPs, magnetar models of these sources are proposed to explain the relevant phenomena [1]. The energy powering the X-ray luminosity in these sources is supplied by the dissipation of superstrong magnetic fields, 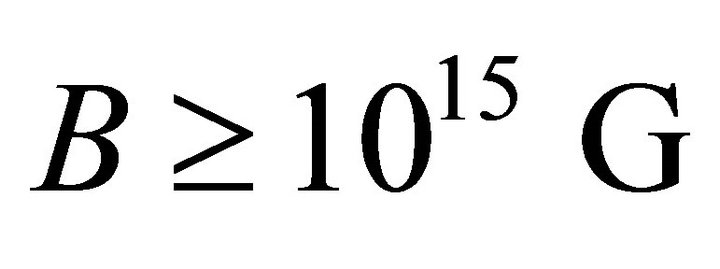 [2] the magnetar outbursts such as giant flares, occur with huge release of magnetic energy ~1044 - 1046 ergs.
[2] the magnetar outbursts such as giant flares, occur with huge release of magnetic energy ~1044 - 1046 ergs.
Experiments & simulations in plasma physics have shown that when two plasmas with oppositely oriented magnetic fields are brought together the magnetic field lines will disconnect and reconnect in a lower energy configuration [3] and a current begins to flow between them; this is referred to as a “current sheet”. A highly twisted magnetic flux loop emerges and comes into contact with an unwound flux loop. It was suggested that more drastic large scale [4] rearrangements or interchanges of magnetic field rather than just reconnection are required to explain the giant SGR flares and also suggest that giant flares are due to enormous displacements of the magnetic field by the neutron star’s core. Being so drastically displaced the magnetic field will rearrange itself into a lower energy configuration, thus releasing an enormous amount of energy in the process. Again it was pointed out that some reconnection [4] events might be expected in the global rearrangement scenario. It is expected that twisted field lines [5] in the magnetosphere could relax by reconnection & release energy which we could observe as SGR bursts. Thus, according to [5] reconnection of field lines in the magnetosphere of magnetar can also give rise to SGR flares.
A tightly wound-up strong magnetic field is assumed to exist inside the magnetars [6] which continually drift outside through the star’s liquid interior, stressing and deforming the crust from interior [7]. It is assumed that the field is not strong enough to drive vertical motion in the crust, but it can drive significant twisting motion of patches of crust along horizontal directions [7]. Patches of a magnetar’s crust can twist elastically, with spiral patterns of shear strain [8]. As a result, the magnetic field lines outside the star anchored to the crust may get twisted with spiral pattern. With reservation for our understanding of reconnection and particle acceleration, we propose here that the bursting activity of SGRs is due to the reconnection-type events in which magnetic energy stored in the non potential (current carrying) magnetic field is released in the magnetosphere. We predict that a twist [8] affects the spin down rate of the neutron star: it causes the magnetosphere to flare out slightly from a pure dipole configuration, thereby increasing the breaking torque acting on the star.
The energy for magnetar flare is stored in the neutron star during its formation. In the magnetar flare, the balance between the reconnection heating and the radiative cooling gives the flare temperature unlike the solar flare controlled by the conductive cooling [9]. In contrast to the common short burst, giant flare with enormous energy and long bursting duration is exceptionally observed from SGRs.
In the space-charge limited flow (SCLF) model, it is assumed that particles are not bound to the neutron star surface by ionic bonding, but instead are freely available. Hence, particles are flowing out at the [10] current density and the corresponding boundary condition is vanishing 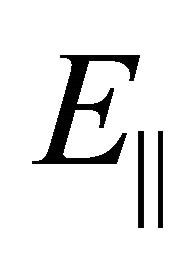 at the neutron star surface. The central idea of SCLF model is that a gap opens which is not shielded by the outflowing charges because
at the neutron star surface. The central idea of SCLF model is that a gap opens which is not shielded by the outflowing charges because 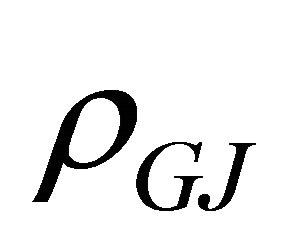 falls off more slowly than the local charge density
falls off more slowly than the local charge density 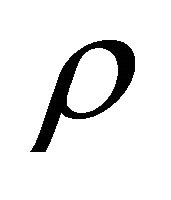 which is proportional to
which is proportional to 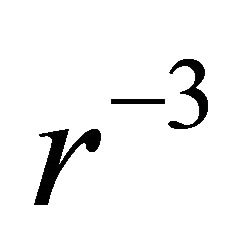 [11], where r is the distance from the stellar centre.
[11], where r is the distance from the stellar centre.
It is expected that “Giant Flares,” are observed from three SGRs: 1999 March 5 from SGR 0526-66: 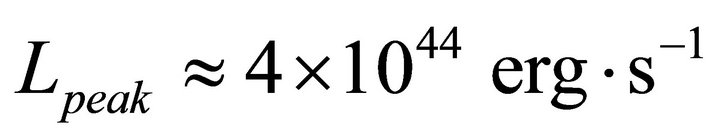 [12]; 1998 August 27 from SGR 1900 + 14:
[12]; 1998 August 27 from SGR 1900 + 14: 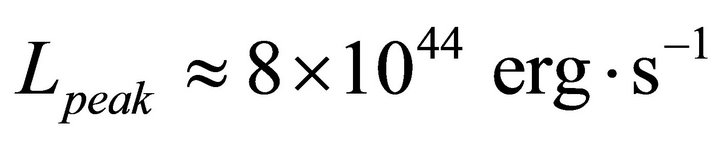 [13] and 2004 December 27 from SGR 1806-20:
[13] and 2004 December 27 from SGR 1806-20:
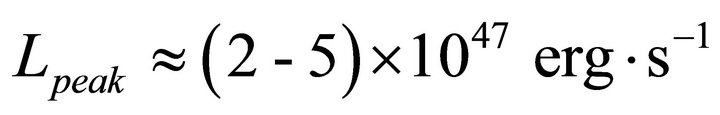 [14]. Hence the giant flare on 2004 December 27 from SGR1806-20 is the most recent and energetic one. It is characterized by an ultra-luminous hard spike, with energy 1046 ergs, lasting ≈0.1 second which decay rapidly into a shoft pulsating tail lasting hundreds of second for main burst. The spectrum of the hard spike is explained by a single blackbody with temperature ≈109 K. In addition, preflare activity with total energy ≈1041 ergs and duration ≈1.0 sec is detected 142 sec before the main burst. Its spectrum is also fitted by a single blackbody with the temperature ≈108 K [15].
[14]. Hence the giant flare on 2004 December 27 from SGR1806-20 is the most recent and energetic one. It is characterized by an ultra-luminous hard spike, with energy 1046 ergs, lasting ≈0.1 second which decay rapidly into a shoft pulsating tail lasting hundreds of second for main burst. The spectrum of the hard spike is explained by a single blackbody with temperature ≈109 K. In addition, preflare activity with total energy ≈1041 ergs and duration ≈1.0 sec is detected 142 sec before the main burst. Its spectrum is also fitted by a single blackbody with the temperature ≈108 K [15].
In reconnection, the shortest timescale is related to the Alfven crossing time of the magnetic structure of length L: 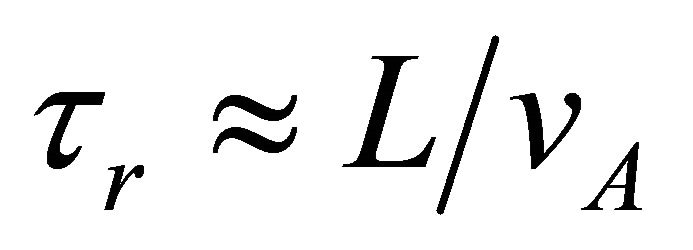 (for the Sun,
(for the Sun,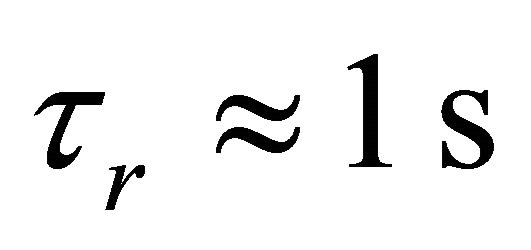 ), the length scale L corresponds to the length of the reconnecting arc, which for the SGRs may be as small as a fracturing of radius and as large as the light-cylinder radius, RLC [5]. For flares occurring close to the surface, they may assume that,
), the length scale L corresponds to the length of the reconnecting arc, which for the SGRs may be as small as a fracturing of radius and as large as the light-cylinder radius, RLC [5]. For flares occurring close to the surface, they may assume that,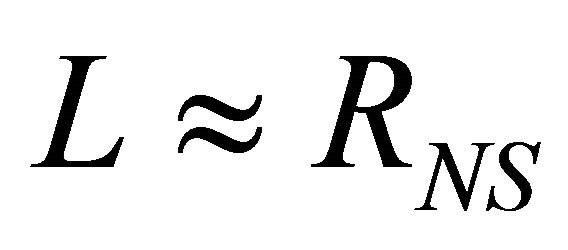 . The Alfven velocity
. The Alfven velocity 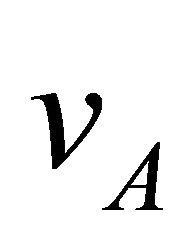 equals the speed of light in the force-free magnetosphere. The observed rise time of the SGR X-ray flares,
equals the speed of light in the force-free magnetosphere. The observed rise time of the SGR X-ray flares, 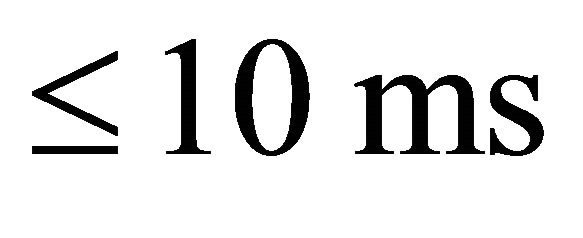 , is consistent with being related to the Alfven time scale. For the observed bursts, the rise time is limited by the intensity of the burst—weaker bursts are expected to have shorter rise times. The shortest rise time is expected to be of the order of light-travel time across the neutron star—tens of microseconds. This time scale also gives the duration of the shortest spikes in the burst structure. The overall duration of the burst depends on the global structure of the reconnection region—the reconnection at one point may trigger reconnection at other points.
, is consistent with being related to the Alfven time scale. For the observed bursts, the rise time is limited by the intensity of the burst—weaker bursts are expected to have shorter rise times. The shortest rise time is expected to be of the order of light-travel time across the neutron star—tens of microseconds. This time scale also gives the duration of the shortest spikes in the burst structure. The overall duration of the burst depends on the global structure of the reconnection region—the reconnection at one point may trigger reconnection at other points.
The goal of this paper is to investigate the flare energy release for pre flare phase and main flare phase at a height of 106 cm and 1010 cm from the stellar centre for the duration of 1.0 second and 0.1 second respectively as our model is confined within the closed magnetic field lines on the basis of giant flare on 2004 December 27 from SGR1806-20. In Section 2 we discuss the expected physical parameters related to magnetar flare as considering the magnetic reconnection in the twisted magnetosphere. Two stages of magnetar flares: preflare phase and main burst activity are discussed & the numerical values of flare luminosities and flare energies are calculated in Section 3. The flare temperature during the magnetic reconnection is discussed in Section 4. Discussions & conclusions are made in Section 5.
2. Expected Physical Parameters Related to Magnetar Flare
A tightly wound up superstrong magnetic field is assumed in the interior of a magnetar which continuously evolves towards the magnetosphere through the solid crust. The crust is deformed due to the magnetic stress and the magnetic field in the magnetosphere anchored with the star gets twisted with spiral pattern which is subjected to displace & reconnect. We concentrate on a class of model where the magnetic reconnection events might be expected by the global rearrangement of displaced magnetic field for which magnetic arcade loops are formed in the magnetar magnetosphere [16]. Due to reconnection of magnetic field in the magnetosphere, it is expected that magnetar will give rise to SGR flares [5].
In this paper we adopt two regions of flares due to reconnection of magnetic fields: the shortest timescale is related to the Alfven crossing time of the magnetic structures of height scale corresponds to the length of the reconnecting arc [5]. We consider magnetic axis is aligned with rotational axis & the first region of flares due to reconnection of magnetic field lines is occurred at the pole of height scale . The exterior magnetic field lines that originate from the pole extend to infinity while the field lines outside the polar cap are closed. Our consideration is limited to a surface at this region where magnetic field will act as natural magnetic funnel. The angular width of the funnel [17] is given by
. The exterior magnetic field lines that originate from the pole extend to infinity while the field lines outside the polar cap are closed. Our consideration is limited to a surface at this region where magnetic field will act as natural magnetic funnel. The angular width of the funnel [17] is given by
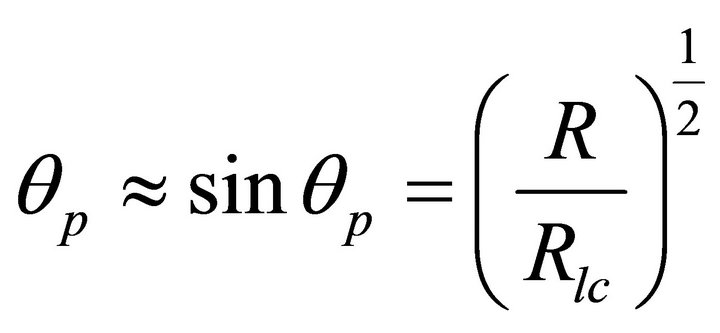
where, R is the radius of the magnetar, 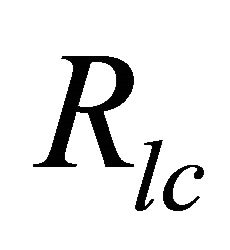 is the radius of the light cylinder = c/Ω, and Ω = Angular velocity = 2π/p, with spin period p. In our choice of parameter, the spin period of magnetar
is the radius of the light cylinder = c/Ω, and Ω = Angular velocity = 2π/p, with spin period p. In our choice of parameter, the spin period of magnetar 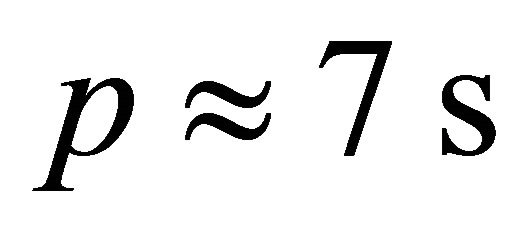 & hence one can find out the corresponding radius of the surface at polar cap
& hence one can find out the corresponding radius of the surface at polar cap 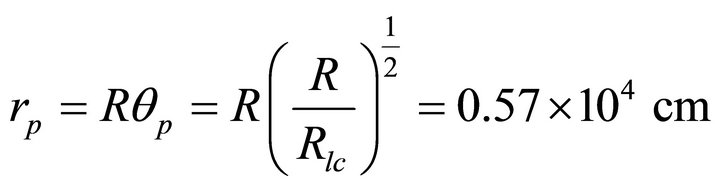 by adopting R
by adopting R
= 106 cm and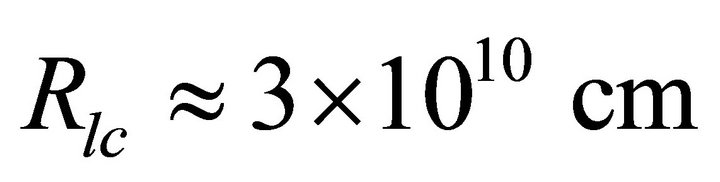 .
.
The second region is considered at a large distance from the stellar centre in the polar region and our reconnection is limited to a surface of natural magnetic funnel at the height scale 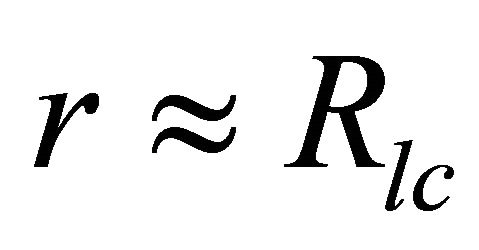 (assuming a spherical surface of radius
(assuming a spherical surface of radius 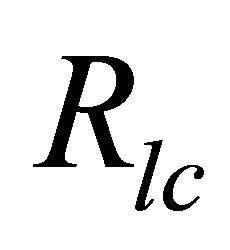 which is confined within the closed magnetic field lines) where the corresponding radius of the surface is given by
which is confined within the closed magnetic field lines) where the corresponding radius of the surface is given by
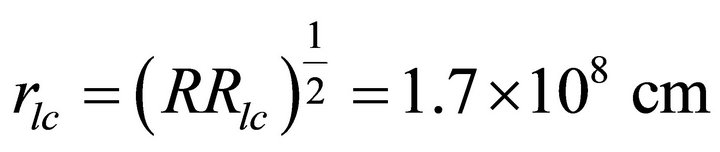 .
.
Presently, the idea that rotating magnetized neutron stars generate huge potential differences between different parts of their surfaces is widely accepted. We consider a uniform magnetic field in the neutron star interior with a potential field outside it [18]. Since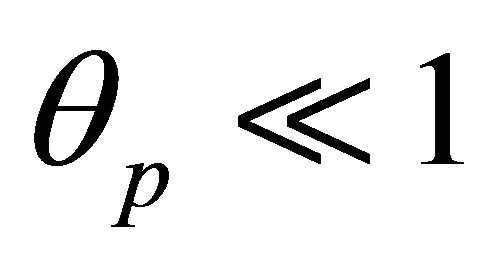 , the maximum potential difference between the centre and the edge of the polar cap can be estimated through the relation
, the maximum potential difference between the centre and the edge of the polar cap can be estimated through the relation
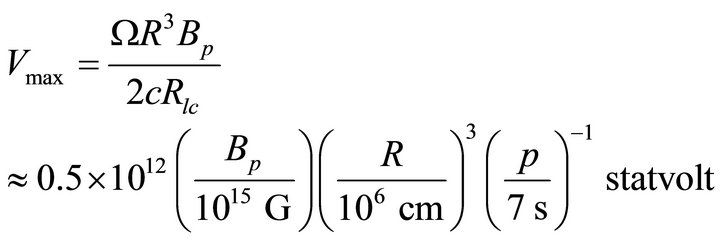 (1)
(1)
across the open field line region. In this paper we assume the magnetic field 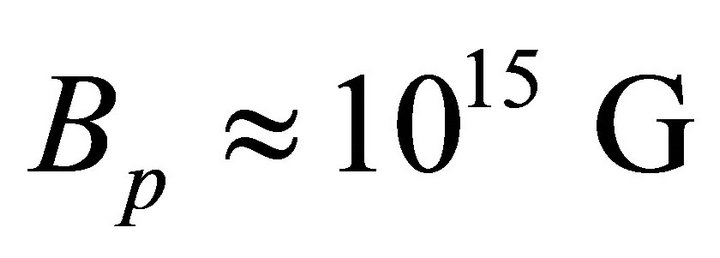 and c is the velocity of light =
and c is the velocity of light =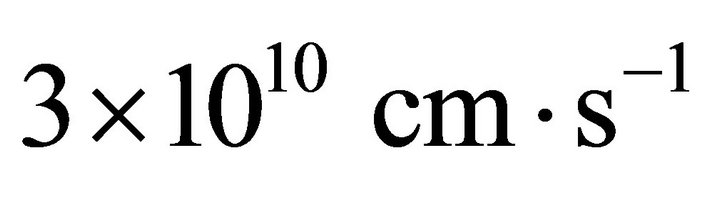 .
.
In applying the space time solution to the electrodynamics of the Polar Cap SCLF model [19], the part of the induced electric field will be left unshielded, and a potential difference [20] at a distance r is obtained through the relation
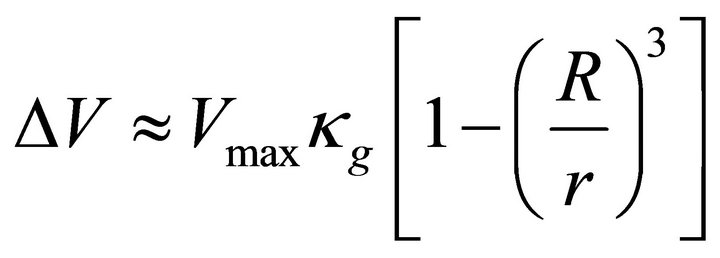 ; for
; for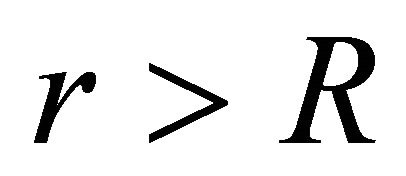 . Where r is the distance from the stellar centre. Here
. Where r is the distance from the stellar centre. Here 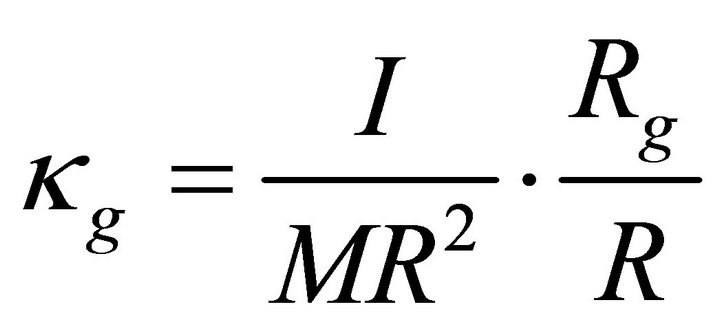 called Relativistic parameter [19], with
called Relativistic parameter [19], with 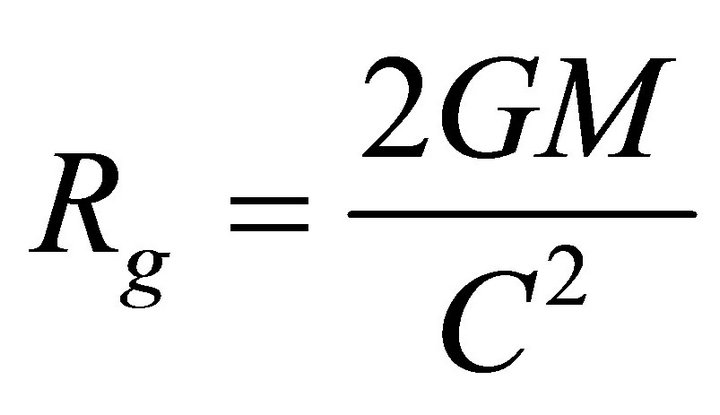 =
=
Schwarzschild radius, 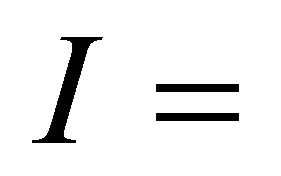 moment of inertia and M = mass of the magnetar. In our case the relativistic parameter
moment of inertia and M = mass of the magnetar. In our case the relativistic parameter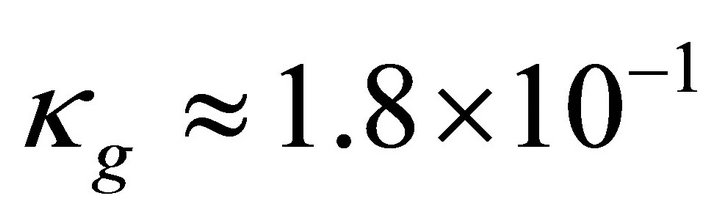 . The potential difference in the polar region of height scale
. The potential difference in the polar region of height scale 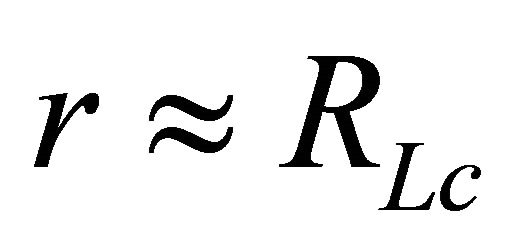 is calculated through the relation
is calculated through the relation
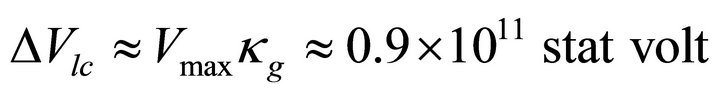 (2)
(2)
Here the term 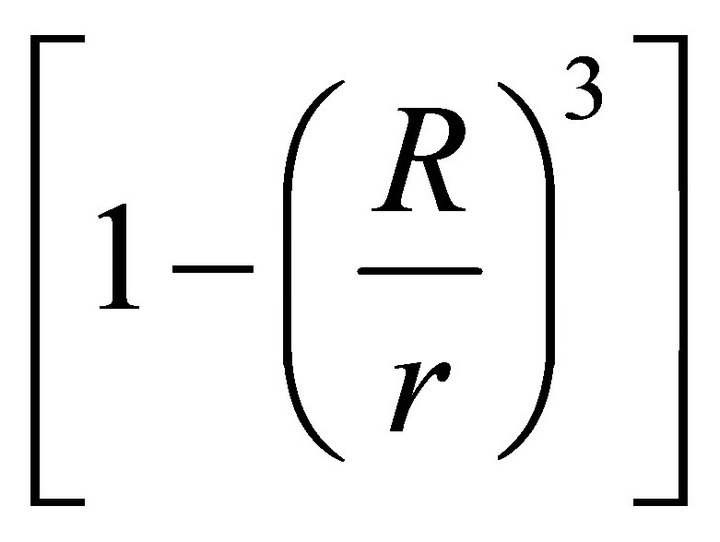 is neglected as the lightcylinder radius
is neglected as the lightcylinder radius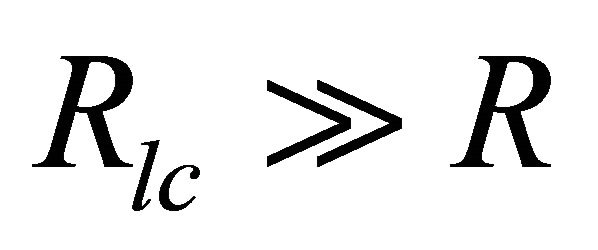 .
.
Proposed a model [8] in which the magnetosphere of a magnetar is threaded by a large-scale current and this current arises from stresses imposed on the crust by highly twisted internal magnetic field. However, experiments and simulations in plasma physics have shown that when two plasmas carrying oppositely oriented magnetic fields are brought to reconnect, a current begins to flow between them [3]. According to Ampere’s law in integral form, current in the edge of polar cap of magnetar
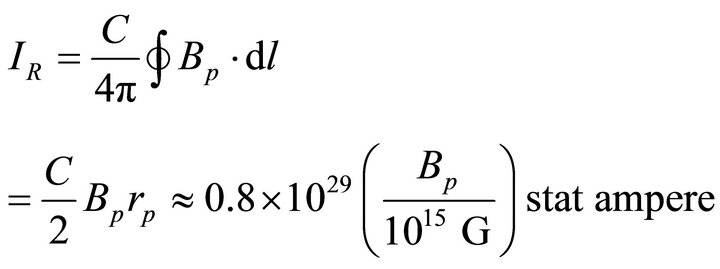 (3)
(3)
In this case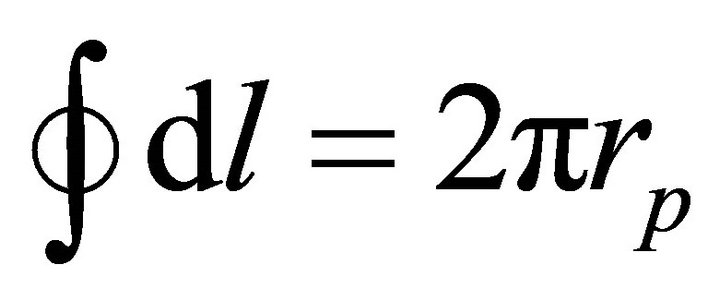 , the perimeter of the surface in polar cap of magnetar with corresponding radius
, the perimeter of the surface in polar cap of magnetar with corresponding radius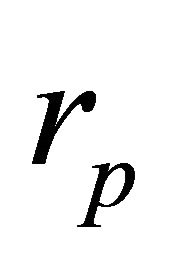 . The reconnection is also assumed to be occurred on the polar region of height scale
. The reconnection is also assumed to be occurred on the polar region of height scale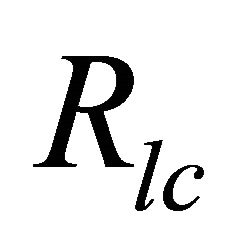 ; hence the current
; hence the current
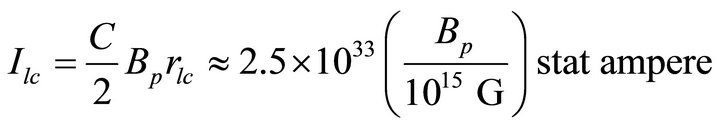 (4)
(4)
In this case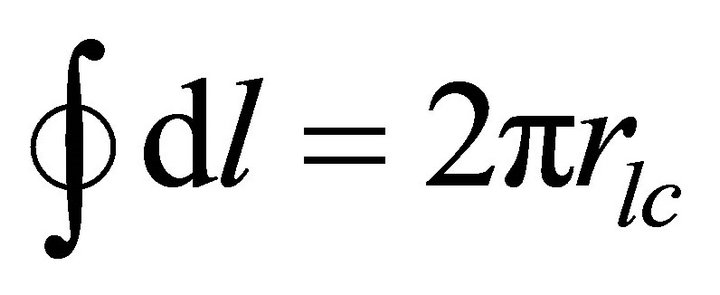 , the perimeter of the surface in the polar region of height scale
, the perimeter of the surface in the polar region of height scale 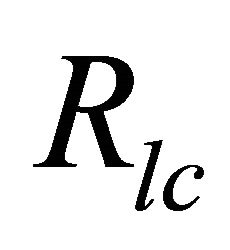 where corresponding radius
where corresponding radius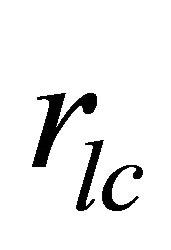 .
.
3. Stages of Magnetar Flare
In this paper we assume two flare phases: (1) preflare activity in the reconnection point on the surface of polar cap 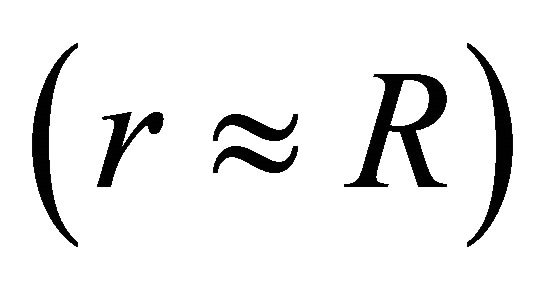 for the duration of 1.0 second, and (2) main burst activity in the reconnection point on the surface of polar cap region of length scale
for the duration of 1.0 second, and (2) main burst activity in the reconnection point on the surface of polar cap region of length scale 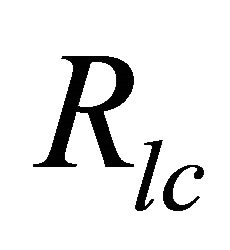 for the duration of 0.1 second for the observation of giant flare on 2004 December 27 from SGR1806-20 [15].
for the duration of 0.1 second for the observation of giant flare on 2004 December 27 from SGR1806-20 [15].
3.1. Preflare Phase
In the preflare phase, the magnetic energy stored in the lower magnetosphere is released via magnetic reconnection. In this case, the height scale r equals to the radius of magnetar R = 106 cm. Here we show the case with flare duration 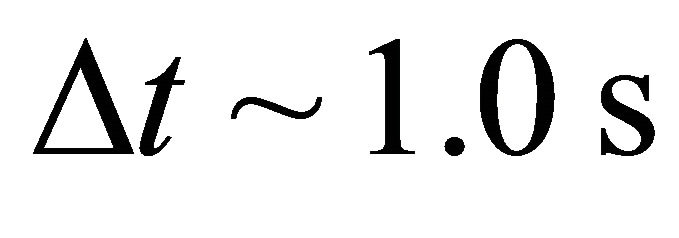 [15] and fixed the size of active region, R = 106 cm. We expect that twisted field lines in the magnetosphere [5] could relax by reconnection and release energy which we would observe as SGR bursts. Adopting the argument that currents flowing outside a magnetar [7] give rise to generate X-rays. Thus, the luminosity of X-rays/γ-rays generated by the reconnection on the magnetar surface is given by
[15] and fixed the size of active region, R = 106 cm. We expect that twisted field lines in the magnetosphere [5] could relax by reconnection and release energy which we would observe as SGR bursts. Adopting the argument that currents flowing outside a magnetar [7] give rise to generate X-rays. Thus, the luminosity of X-rays/γ-rays generated by the reconnection on the magnetar surface is given by
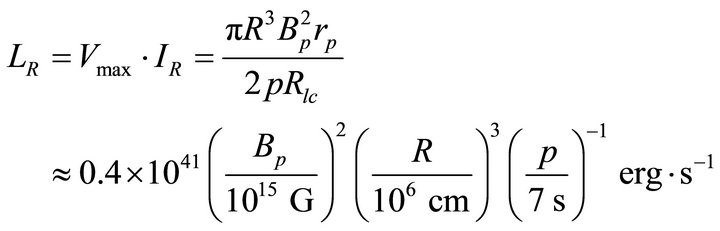 (5)
(5)
Based on the magnetic reconnection model for solar flare [21] the release rate of magnetic flare due to magnetic reconnection ≈Erec/trec is obtained as the γ-ray luminosity from the surface of magnetar 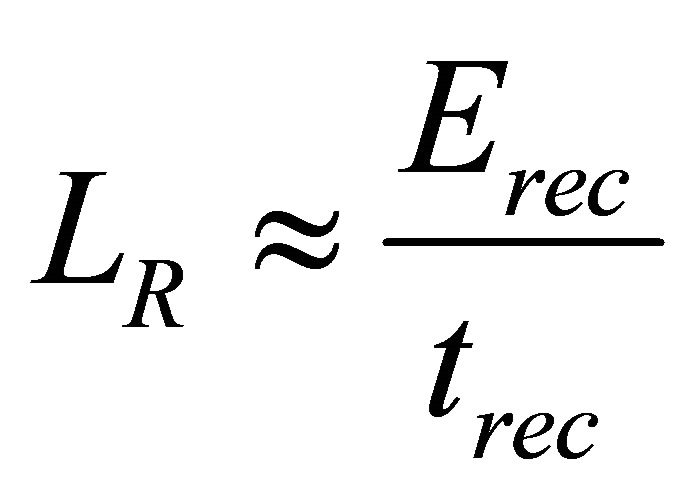 where Erec is the released energy during the reconnection and trec is the typical timescale of the reconnection. Assuming the typical timescale of the reconnection trec is equal to the flare duration Δt; thus the released energy is termed as γ-ray radiation from the magnetar surface
where Erec is the released energy during the reconnection and trec is the typical timescale of the reconnection. Assuming the typical timescale of the reconnection trec is equal to the flare duration Δt; thus the released energy is termed as γ-ray radiation from the magnetar surface
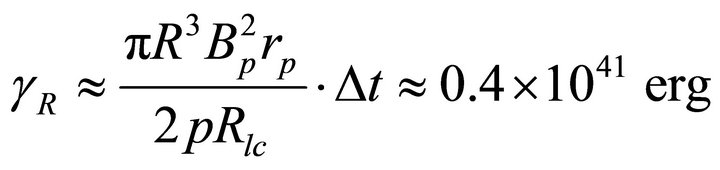 (6)
(6)
where Δt is the preflare duration in units 1 s.
3.2. Main Burst Phase
After the preflare phase, transports the released magnetic energy to the upper magnetosphere and heats the magnetar crust. In this case we observe the main burst is occurred after 142 s of preflare and the height of the reconnection point is considered of height scale 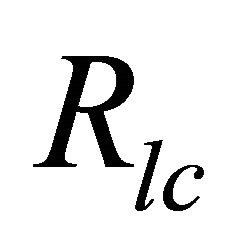 [5]. For the force free magnetosphere, the Alfven velocity
[5]. For the force free magnetosphere, the Alfven velocity 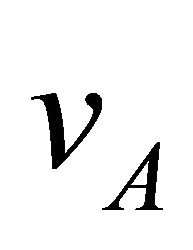 equals the speed of light for which the time scale
equals the speed of light for which the time scale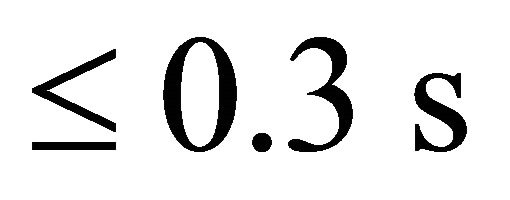 . Here we observe the burst with the flare duration Δt ≈ 0.1 s [15]. The γ-ray luminosity in the polar cap region of height scale
. Here we observe the burst with the flare duration Δt ≈ 0.1 s [15]. The γ-ray luminosity in the polar cap region of height scale 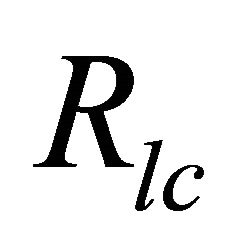
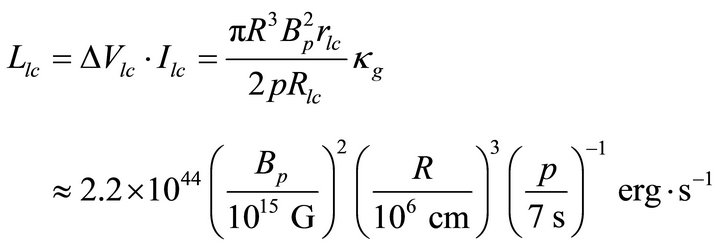 (7)
(7)
And the γ-ray radiated from the polar region of height scale 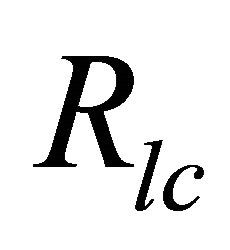
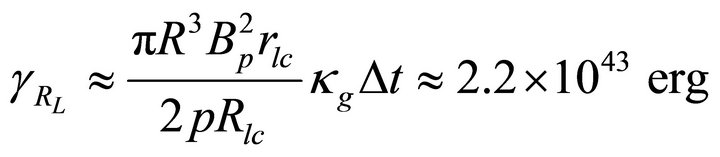 (8)
(8)
Assuming the height scale of reconnection region as shown in Table 1 and find the corresponding radii by using the relations 
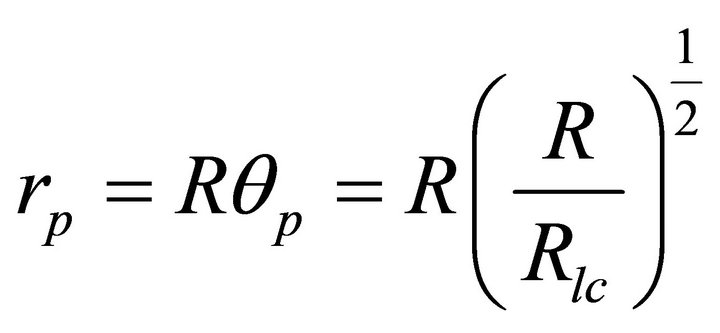 and
and 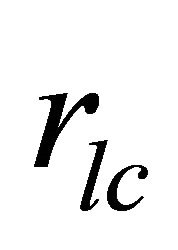
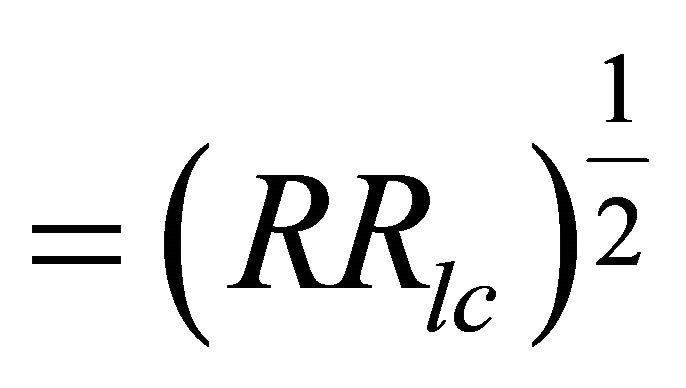 ; we obtain γ-ray luminosities by applying the Equation (5) for
; we obtain γ-ray luminosities by applying the Equation (5) for  and Equation (7) for
and Equation (7) for 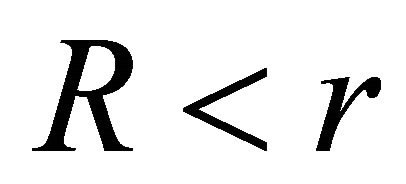
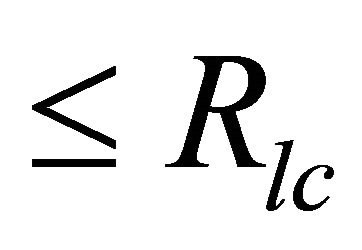 and plotted a graph as shown in Figure 1.
and plotted a graph as shown in Figure 1.
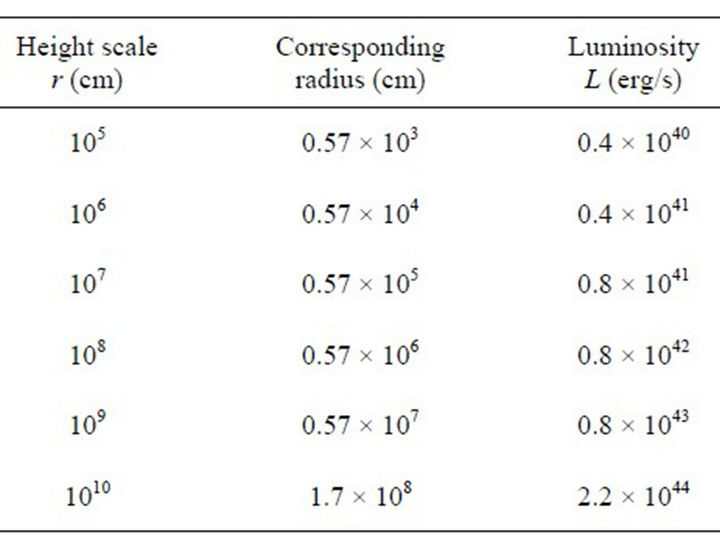
Table 1. Height scale of reconnection region from the stellar centre, corresponding radii of the surfaces of magnetic funnels and the luminosities of magnetar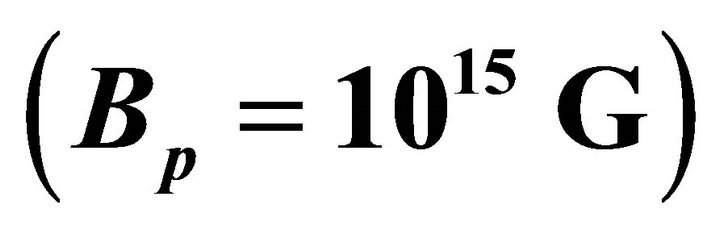 .
.
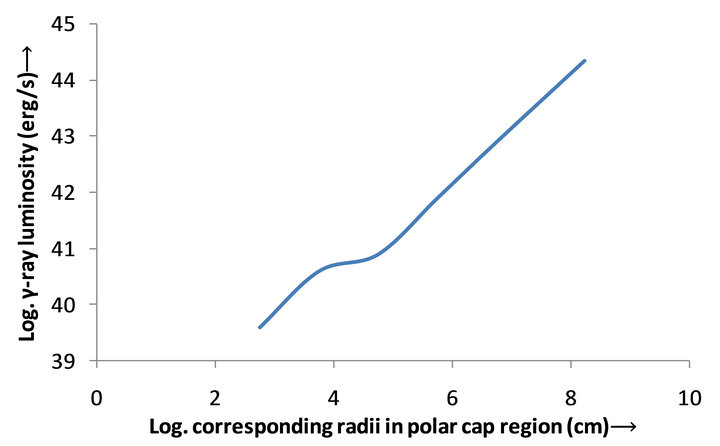
Figure 1. Log. corresponding radii in the polar cap region in cm against Log. γ-ray luminosity in erg·s−1 is plotted.
From Table 1, it is observed that the luminosity for the range of height scale 106 - 107 cm almost same and the luminosities for the remaining part uniformly increase and it extend up to radius of light cylinder which is confined in this paper.
In Figure 1, the platform region in the curve is observed due to almost constant luminosity on the surface of magnetar. On the surface of magnetar, the potential is maximum and out of the surface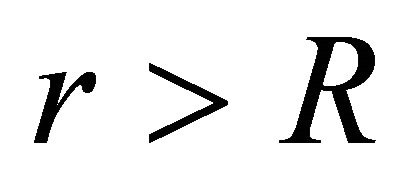 , we apply the relation,
, we apply the relation, 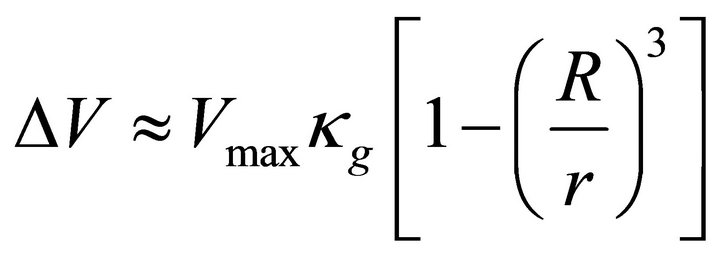 , where the term
, where the term 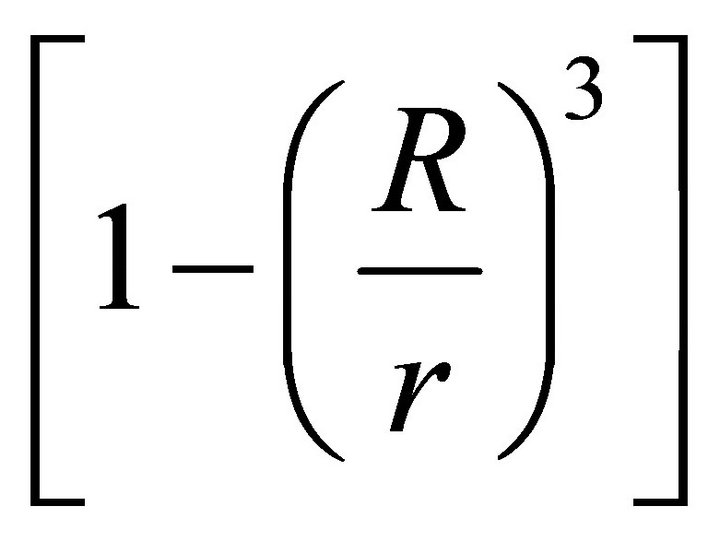 is neglected.
is neglected.
4. Temperature during the Flare
Radiative cooling dominates over the conductive cooling in magnetar flare [9]. The flare temperature of magnetar is thus determined by the balanced between the reconnection heating and the radiative cooling. Considering that black body cooling retains the thermal balanced of the system, the balance equation is,
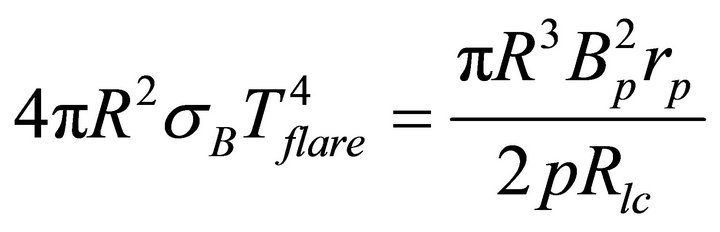 (9)
(9)
where 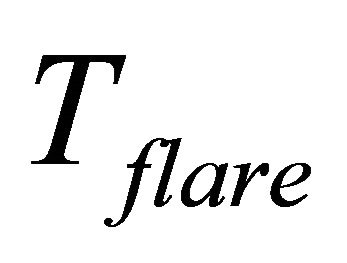 the flare temperature of the reconnection region during the flare energy releases, and
the flare temperature of the reconnection region during the flare energy releases, and 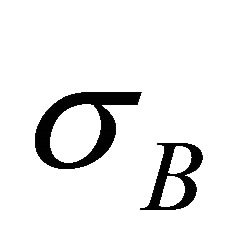 is the Stefan-Boltzmann constant ≈5.67 × 10‒5 erg·sec‒1 (cm‒2·K‒4). This gives the flare temperature of the reconnection region during the flare energy release from the polar cap near the surface of magnetar
is the Stefan-Boltzmann constant ≈5.67 × 10‒5 erg·sec‒1 (cm‒2·K‒4). This gives the flare temperature of the reconnection region during the flare energy release from the polar cap near the surface of magnetar
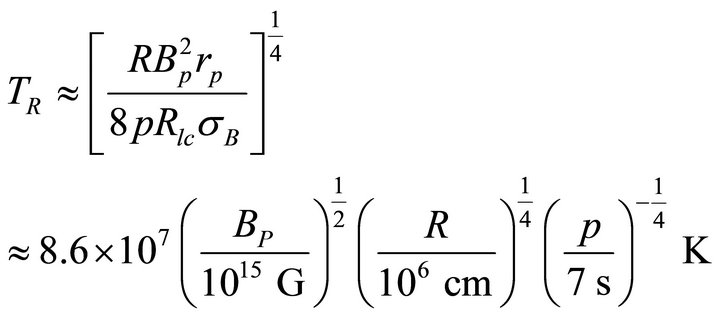 (10)
(10)
Flare temperature for main burst activity on the polar cap region of length scale 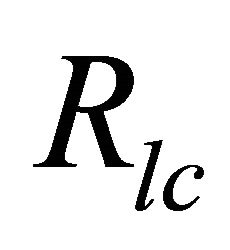
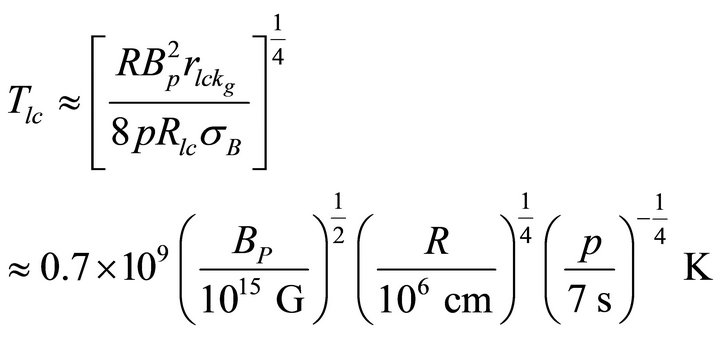 (11)
(11)
Adopting the calculated γ-ray luminosities and using the equation (10) for condition  and equation (11) for
and equation (11) for , we calculate the flare temperature,
, we calculate the flare temperature, 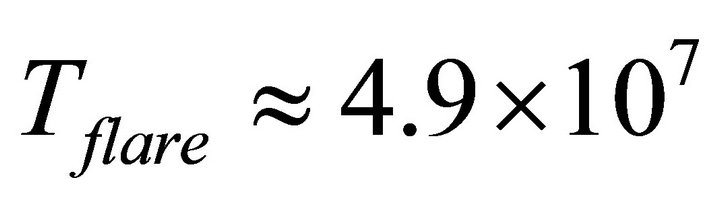 , 8.6 × 107, 1.02 × 108, 1.8 × 108, 3.2 × 108, and
, 8.6 × 107, 1.02 × 108, 1.8 × 108, 3.2 × 108, and 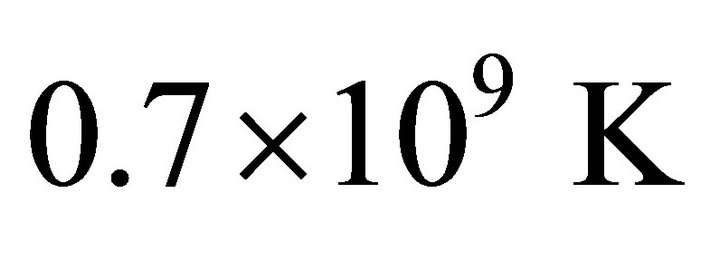 and a graph is plotted in Figure 2.
and a graph is plotted in Figure 2.
The effect of γ-ray luminosity on the flare temperature can be remarkable which could increase normally by changing the order of magnitudes of luminosity. It may also be shown that the graph of the flare temperatures would be changed for varying the magnetic fields. These are consistent with the observation of the preflare and main burst activity with the giant flare of 2004 December 27 from SGR 1806-20 [15].
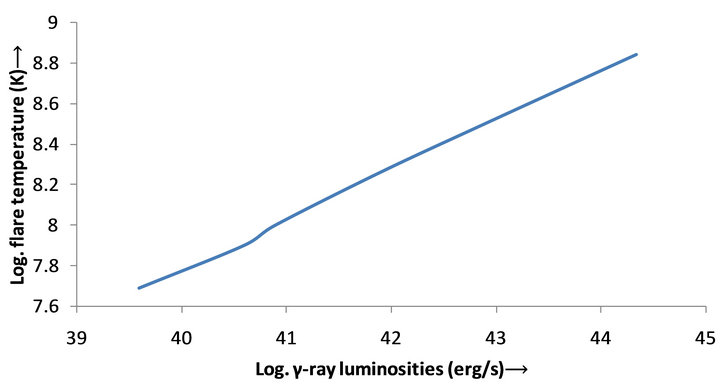
Figure 2. Log. γ-ray luminosities in erg·s−1 against Log. Temperature during the flare in K is plotted.
5. Discussions and Conclusions
It is observed that magnetic field of magnetar plays an important role in the generation of X-ray as well as γ-ray from magnetar surface. The magnetic field strengths of magnetars are typically found to be 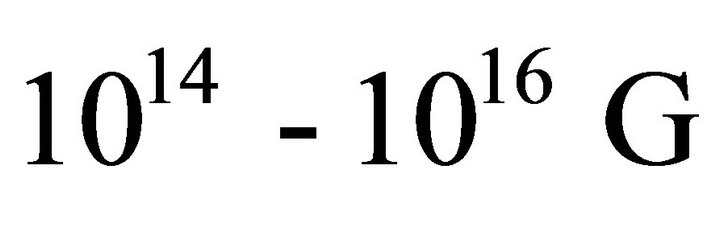 and may be as large as
and may be as large as 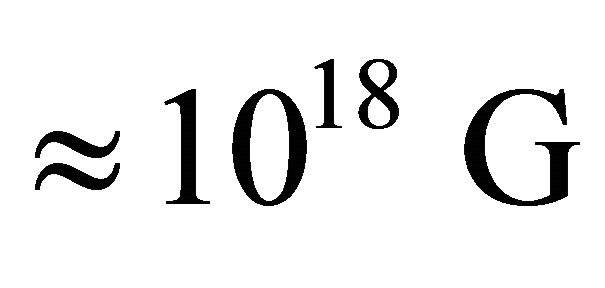 [22] for which the luminosity of magnetar can be obtained to be
[22] for which the luminosity of magnetar can be obtained to be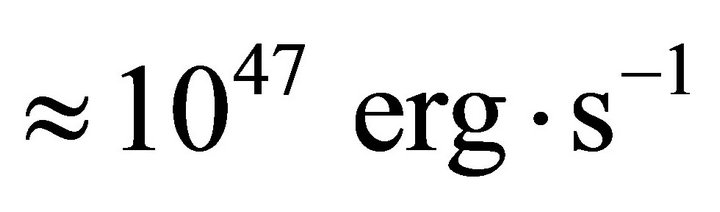 .
.
It was pointed out that rotating magnetized neutron [23] stars are unipolar inductors that generate huge potential drops, 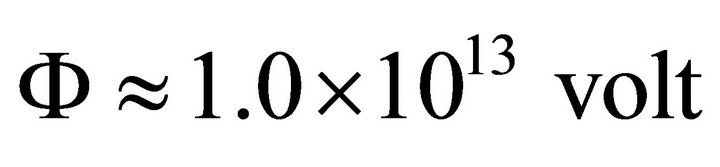 , across the open field line region, for the set of parameters,
, across the open field line region, for the set of parameters, 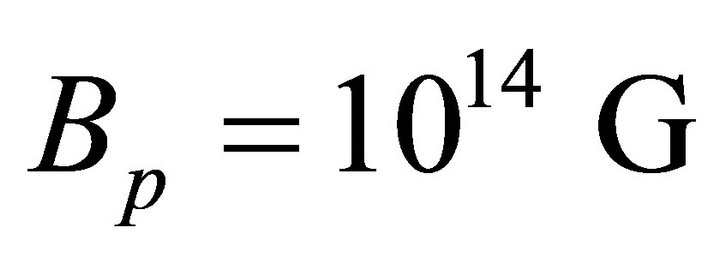 , p = 8 s, and R = 106 cm. Under certain conditions, a part, or even total amount of this potential will drop across a chargeddepleted region (or a gap) formed in the polar cap area of the pulsar.
, p = 8 s, and R = 106 cm. Under certain conditions, a part, or even total amount of this potential will drop across a chargeddepleted region (or a gap) formed in the polar cap area of the pulsar.
The oblique rotator certainly is a more realistic model than the aligned rotator, since its manifestly broken axial symmetry naturally leads to radiation modulated at the angular frequency Ω. Relativistic particle-in-cell simulations [24] seem to indicate that a plasma filled magnetosphere around an oblique rotator leads to an outflow of particles along the equatorial belt as well as along the rotation axis.
It is predicted from the observation [25], if the temperature (T) in the upper atmospheric layers reaches to thermal radiation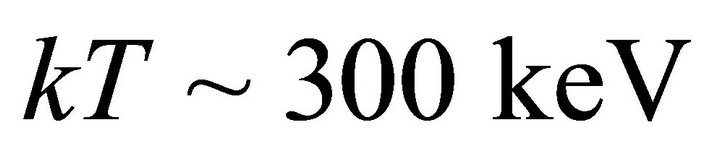 , (k is the Boltzmann constant = 1.38 × 10‒23 J·K‒1) then electron-positron pairs are created directly in the magnetosphere by the conversion of thermal bremsstrahlung photons off the magnetic field. In this paper, we examine the thermal radiation from the magnetosphere and it is expected that electron-positron pair would be created in a transition layer within the magnetosphere of the magnetar.
, (k is the Boltzmann constant = 1.38 × 10‒23 J·K‒1) then electron-positron pairs are created directly in the magnetosphere by the conversion of thermal bremsstrahlung photons off the magnetic field. In this paper, we examine the thermal radiation from the magnetosphere and it is expected that electron-positron pair would be created in a transition layer within the magnetosphere of the magnetar.
In this paper we examined the different values of luminosities, γ-rays, and temperatures of magnetar and compared with the observed values of the giant flare on 2004 December 27 from SGR1806-20 [15] very well. The agreement between the observation and our theoretical model would be indirect evidence of magnetic reconnection model commonly in solar and magnetar flare.
6. Acknowledgements
The authors would like to express thanks to Prof. H. L. Duorah, for his valuable help and fruitful discussions.
REFERENCES
- R. C. Duncan and C. Thompson, “Formation of Very Strongly Magnetized Neutron Stars-Implication for Gamma-Ray Bursts,” Astrophysical Journal, Vol. 392, No. 1, 1992, pp. L9-L13. doi:10.1086/186413
- C. Thompson and R. C. Duncan, “The Soft Gamma Repeaters as Very Strongly Magnetized Neutron Stars. II: Quiescent Neutrino, X-Ray, and Alfven Wave Emission,” Astrophysical Journal, Vol. 473, No. 1, 1996, p. 322. doi:10.1086/178147
- T. Tajima and K. Shibata, “Plasma Astrophysics,” Addison-Wesley, Reading, 1997.
- C. Thompson and R. C. Duncan, “The Soft Gamma Repeaters as Very Strongly Magnetized Neutron Stars-I: Radiative Mechanism for Outbursts,” Monthly Notices of the Royal Astronomical Society, Vol. 275, No. 2, 1995, pp. 255-300.
- M. Lyutikov, “Radio Emission from Magnetars,” Astrophysical Journal, Vol. 580, No. 1, 2002, pp. L65-L68. doi:10.1086/345493
- C. Thompson and R. C. Duncan, “The Giant Flare of 1998 August 27 from SGR1900+14, II: Radiative Mechanism and Physical Constraints on the Source,” Astrophysical Journal, Vol. 561, No. 2, 2001, pp. 980-1005. doi:10.1086/323256
- C. Thompson, R. C. Duncan, P. M. Woods, C. Kouveliotou, M. H. Finger and van Paradijs, “Physical Mechanisms for the Variable Spin-Down and Light Curve of SGR1900+14,” Astrophysical Journal, Vol. 543, No. 1, 2000, pp. 340-350. doi:10.1086/317072
- C. Thompson, M. Lyutikov and S. R. Kulkarni, “Electrodynamics of Magnetars: Implications for the Persistent XRay Emission and Spin-Down of the SGRs and AXPs,” Astrophysical Journal, Vol. 574, No. 1, 2002, pp. 332- 355. doi:10.1086/340586
- K. Shibata and T. Yokoyama, “Origin of the Universal Correlation between the Flare Temperature and the Emission Measure for Solar and Stellar Flares,” Astrophysical Journal, Vol. 526, No. 1, 1999, pp. L49-L52. doi:10.1086/312354
- P. Goldreich and W. H. Julian, “Pulsar Electrodynamics,” Astrophysical Journal, Vol. 157, No. 2, 1969, p. 869. doi:10.1086/150119
- E. T. Scharlemann, J. Arons and W. M. Fawley, “Potential Drops above Pulsar Polar Caps-Ultrarelativistic Particle Acceleration along the Curved Magnetic Field,” Astrophysical Journal, Vol. 222, No. 1, 1978, pp. 297-316. doi:10.1086/156144
- E. P. Mazets, S. V. Golenetskii, V. N. Ilinskii, R. L. Aptekar and I. A. Guryan, “Observations of a Flaring X-Ray Pulsar in Dorodo,” Nature, Vol. 282, 1979, pp. 587-589.
- K. Hurley, et al., “A Giant Periodic Flare from the Soft γ-Ray Repeater SGR1900+14,” Nature, Vol. 397, No. 6714, 1999, pp. 41-43. doi:10.1038/16199
- D. M. Palmer, et al., “A Giant Gamma-Ray Flare from the Magnetars SGR1806-20,” Nature, Vol. 434, No. 7037, 2005, pp. 1107-1109. doi:10.1038/nature03525
- S. E. Boggs, et al., “The Giant Flare of 2004 December 27 from SGR1806-20,” Astrophysical Journal, Vol. 661, No. 1, 2007, pp. 458-467. doi:10.1086/516732
- Y. Masada, “Dead Zone Formation and Non-Steady Hyperaccretion in Collapsar Disks,” Proceedings of the International Astronomical Union, Vol. 4, No. S259, 2009, pp. 119-120. doi:10.1017/S1743921309030269
- W. A. Baan and A. Treves, “On the Pulsation of X-Ray Sources,” Astronomy & Astrophysics, Vol. 22, 1973, p. 421.
- E. Flowers and M. A. Ruderman, “Evolution of Pulsar Magnetic Fields,” Astrophysical Journal, Vol. 215, No. 1, 1977, pp. 302-310. doi:10.1086/155359
- A. G. Muslimov and A. I. Tsygan, “General Relativistic Electric Potential Drops above Pulsar Polar Cap,” Monthly Notices of the Royal Astronomical Society, Vol. 255, No. 3, 1992, pp. 61-70.
- B. Rudak, J. Dyks and T. Bulik, “High-Energy Radiation from Pulsars: A Challenge to Polar-Cap Models, Prpc. of 270. WE-Heraeus Seminar, Neutron Stars, Pulsars and Supernova Remnants,” 2002.
- E. Priest and T. Forbes, “Magnetic Reconnection: MHD Theory and Applications,” Cambridge University Press, New York, 2000. doi:10.1017/CBO9780511525087
- D. Lai, “Matter in Strong Magnetic Fields,” Review of Modern Physics, Vol. 73, No. 3, 2001, pp. 629-661. doi:10.1103/RevModPhys.73.629
- B. Zhang and A. K. Harding, “Full Polar Cap Cascade Scenario: Gamma-Ray and X-Ray Luminosities from SpinPowered Pulsars,” Astrophysical Journal, Vol. 535, No. 2, 2000, pp. 1150-1171. doi:10.1086/308598
- A. Spitkovsky and J. Arons, “Simulations of Pulsar Wind Formation,” Astronomical Society of the Pacific Conference Series, 2002.
- C. Thompson and A. M. Beloborodov, “High-Energy Emission from Magnetars,” Astrophysical Journal, Vol. 634, No. 1, 2005, pp. 565-569. doi:10.1086/432245

