International Journal of Astronomy and Astrophysics
Vol.1 No.2(2011), Article ID:5578,4 pages DOI:10.4236/ijaa.2011.12015
An Intrinsic Relation between a Function of the Right Ascension and Declination with the Angular Distance to the Vertex for Hyades Stars
1Astronomy Department, Faculty of Science, King Abdul Aziz University, Jeddah, Saudi Arabia
2Mathematics Department, Faculty of Science, University of Dammam, Dammam, Saudi Arabia
E-mail: Sharaf_adel@hotmail.com, hassanselim@yahoo.com
Received February 16, 2011; revised April 22, 2011; accepted April 30, 2011
Keywords: Ttechniques, Astrometry and Kinematic, Moving Clusters, Open Clusters-Hyades Cluster
Abstract
In this paper, an intrinsic relation was developed for Hyades stars between a function of the right ascensions  and declination
and declination  with the angular distance
with the angular distance  from the vertex. The precision criteria of this relation are very satisfactory and a correlation coefficient of value
from the vertex. The precision criteria of this relation are very satisfactory and a correlation coefficient of value  1 was found which proves that the attributes are completely related linearly.
1 was found which proves that the attributes are completely related linearly.
1. Introduction
Hyades is an open cluster occupies a unique place in the history and literatures of astronomy. It is one of the few star clusters to have been recognized by the ancients, and shares with the Pleiades and Coma clusters the distinction of being sufficiently close to us for the brighter members to be individually visible to the naked eye. Hyades cluster, with some possible members, a total mass of some 300 - 400 Solar mass. Since no strict information is gathered for the chemical composition of the Hyades cluster, as a result of degeneracy in the color-magnitude diagram, then by adopting hydrogen abundance [1] to be X = 0.676, it was found that, the age to be 670 Myr, while by adopting hydrogen abundance to be X = 0.718, the age is 720 Myr. Hyades has an extension in the sky of about 20˚. Hyades cluster provides a well known example of a moving cluster, that is a group of stars whose parallel motions in space yield, on the celestial sphere, directions of proper motion that appear to converge to a point called the vertex of the motion (or of the cluster). The determination of the equatorial coordinates of the vertex, that is, its right ascension and declination (A, D) is one of the most important problem in the kinematical, astrometry and physical studies of moving clusters [2-6]. In particular, the color –magnitude diagram of the Hyades cluster has been of prime importance in establishing the Zero Age Main Sequence (ZAMS) as well as in calibrating luminosity criteria which permit the determination of the absolute magnitudes of the stars from observable features in their spectra [7,8]. In fact the determination of the mass functions of open clusters of different ages allows us to infer the efficiency with which brown dwarfs are evaporated from clusters to populate the field. Very recently [9] compare the mass function of Praesepe cluster and Hyades cluster ( nearly of the same age), it was found out that their mass functions differs significantly, indicating that the two clusters did not have the same initial mass function, or that dynamical evolution (e.g. evaporation of low mass members) has proceeded differently in the two clusters. Recently, new method for the statistical determination of open cluster metallicities was established [10] and applied to the Hyades. The importance of the study of cluster metallicities helps to understand the local stellar formation and evolution throughout the Milky Way.
The kinematic distance of the Hyades derived from a combination of proper motions and spectroscopic radial velocities, has been one of the fundamental starting points for the calibration of the photometric distance scale [3,5,11].
In fact, the availability of the final results of the Hipparcos mission, provide a radical improvement in astrometry data on all stars. In Hipparcos observing program, including approximately 240 candidate Hyades members, the first detailed study distance, structure, membership, dynamics and age of the Hyades cluster, using Hipparcos data [8]. Relation between apparent magnitude and parallax was developed [12].
Also, on a detailed analysis of the binaries of the Hyades, in which the masses of the components are well known, it was shown that, there is a very definite relationship between the mixing-length parameter and the stellar mass [1].
In the present paper, an intrinsic relation was developed for Hyades stars between a function of the right ascensions  and declination
and declination 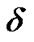 with the angular distance
with the angular distance  from the vertex. As a test for the existence of such relation for Hyades cluster, we used 133 stars of Schwan's table [11]. The precision criteria of the relation are very satisfactory and a correlation coefficient of value
from the vertex. As a test for the existence of such relation for Hyades cluster, we used 133 stars of Schwan's table [11]. The precision criteria of the relation are very satisfactory and a correlation coefficient of value  1 was found which proves that the attributes are completely related linearly.
1 was found which proves that the attributes are completely related linearly.
List of symbols Before staring, we see profitable to list the symbols appear in the present paper
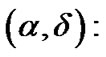 The right ascension and declination
The right ascension and declination
 : The components of the proper motion
: The components of the proper motion 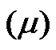 in the right ascension and declination.
in the right ascension and declination.
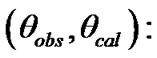 The observed and calculated position angles of the total proper motion
The observed and calculated position angles of the total proper motion 
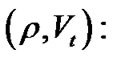 The radial and tangential velocities.
The radial and tangential velocities.
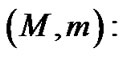 The absolute and apparent magnitudes p: The parallax.
The absolute and apparent magnitudes p: The parallax.
V: The velocity of the cluster.
d: The distance of the cluster
 The right ascension and declination of the vertex of the cluster.
The right ascension and declination of the vertex of the cluster.
 The angular distance of a star from the vertex of the cluster.
The angular distance of a star from the vertex of the cluster.
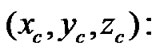 The heliocentric coordinates of the center of the cluster.
The heliocentric coordinates of the center of the cluster.
2. Basic Formulations
2.1. Best Rational Approximation
In what follows, we shall develop an algorithm for the best rational approximation  to a discrete function, f(x), in the least-squares sense.
to a discrete function, f(x), in the least-squares sense.
Given positive integers ,
, 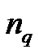 and N, arguments
and N, arguments , and function values
, and function values ;
;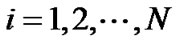 .The problem is to determine the coefficients of the polynomials:
.The problem is to determine the coefficients of the polynomials:
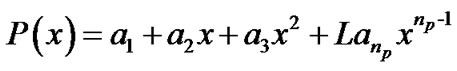
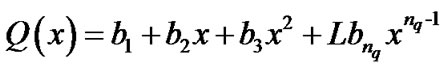
Such that
 = minimum (1)
= minimum (1)
A direct approach to the problem (1) leads to a system of nonlinear equations. Therefore, the problem is reformulated in the following way:
Let  and
and  be an approximate solution to (1).The problem is then to determine the increments
be an approximate solution to (1).The problem is then to determine the increments 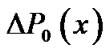 and
and  such that:
such that:
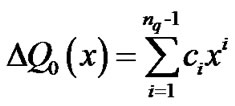 ;
; 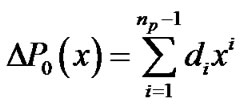 where we assume, without loss of generality that, the constant term of
where we assume, without loss of generality that, the constant term of 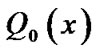 remains unchanged, that is, the constant term
remains unchanged, that is, the constant term  of
of 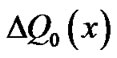 is zero. By letting
is zero. By letting  in the second sum, then the problem reduces to that of determining the c’s coefficients of the increments
in the second sum, then the problem reduces to that of determining the c’s coefficients of the increments 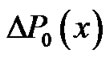 and
and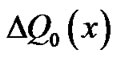 , where
, where
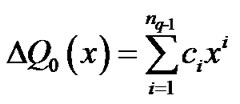 , (2)
, (2)
 , (3)
, (3)
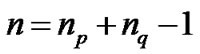 . (4)
. (4)
The minimization problem of Equation (1) then becomes:
 . (5)
. (5)
Linearizing  with respect to
with respect to  and
and 
we get.
 . (6)
. (6)
Using Equation (6) into Equation (5) gives the approximation , where
, where
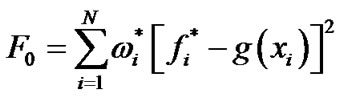 , (7)
, (7)
 , (8)
, (8)
 , (9)
, (9)
 . (10)
. (10)
Using Equations (2) and (3) into Equation (10) we get
 , (11)
, (11)
 ;
; , (12)
, (12)
 ;
; . (13)
. (13)
Now the coefficients  are determined so that
are determined so that . This is a typical weighted linear least squares [13] with function values
. This is a typical weighted linear least squares [13] with function values , weights
, weights  and fundamental functions
and fundamental functions  and leads to a system of linear equations
and leads to a system of linear equations
 , (14)
, (14)
with H symmetric positive semi-definite coefficient matrix, where
 , (15)
, (15)
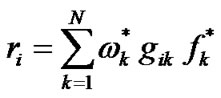 (16)
(16)
And
 . (17)
. (17)
Given a solution  and
and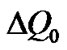 to the problem
to the problem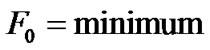 , a new approximation is formed using
, a new approximation is formed using
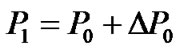 ,
,
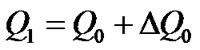 .
.
In general, given approximation 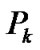 and
and  increments
increments 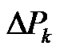 and
and  are determined as indicated above, and the next approximation are:
are determined as indicated above, and the next approximation are:
 , (18)
, (18)
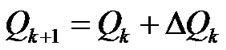 (19)
(19)
This process is started with some initial approximation, usually with 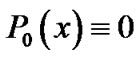 and
and  and is stopped when there is indication of convergence according to certain criteria (Equation (20) or Equation (21)).
and is stopped when there is indication of convergence according to certain criteria (Equation (20) or Equation (21)).
2.2. Refinement of the Calculation Procedure
The above approach has two defects:
1) There is no guarantee for improvement of the rational fit obtained with successive iterations if the initial approximation is not close enough to a true solution.
2) Zeros may come into the denominator, causing a complete breakdown of the procedure. To overcome these defects we use Press's approach [14] as follows: Let.
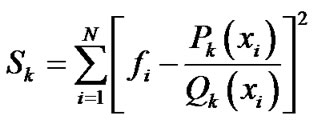 .
.
Then, instead of using the relations (18) and (19) we use
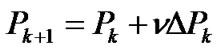 ,
,  where the relaxation factor
where the relaxation factor  is chosen so that
is chosen so that  is close to a minimum when regarded as a function of
is close to a minimum when regarded as a function of 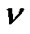 and
and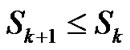 .Choosing
.Choosing  sufficiently small also prevents zeros from entering the denominator.
sufficiently small also prevents zeros from entering the denominator.
2.3. Convergence Criteria
Let  denote the sum of the absolute values of the coefficients of
denote the sum of the absolute values of the coefficients of 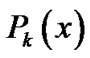 and
and 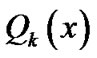 Then, the process is stopped if either.
Then, the process is stopped if either.
 (20)
(20)
 . (21)
. (21)
3. Relation between H and 
By using Schwan’s table [11] and the computational algorithm of Sharaf et al. [6], we get for A and D together with their probable errors the values 
 Then by using the rational model of Section 2, we get new relation between
Then by using the rational model of Section 2, we get new relation between  and the angular distance to the vertex
and the angular distance to the vertex 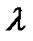 as:
as:
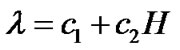 , (22)
, (22)

(23)
Where the coefficients and the error analysis of the model can be obtained using [13] as:
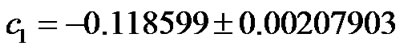
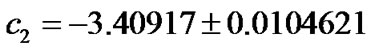
The probable error of the fit is 
The average squared distance between the exact solution and the least squares solution 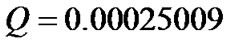
The linear correlation coefficient between 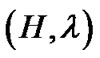 is
is 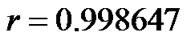
The graphical representation between the raw and the fitted data is given in Figure 1.
The distribution of the residual errors between the raw and the fitted data is shown in Figure 2.
4. Conclusions
In concluding the present paper, a relation was developed for Hyades stars between a function of the right ascensions  and declination
and declination 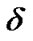 with the angular distance
with the angular distance 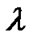 from the vertex. The precision criteria of this relation are very satisfactory and a correlation coefficient of value
from the vertex. The precision criteria of this relation are very satisfactory and a correlation coefficient of value 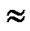 1 was found which proves that the attributes are completely related linearly. Consequently, we can say that,
1 was found which proves that the attributes are completely related linearly. Consequently, we can say that,
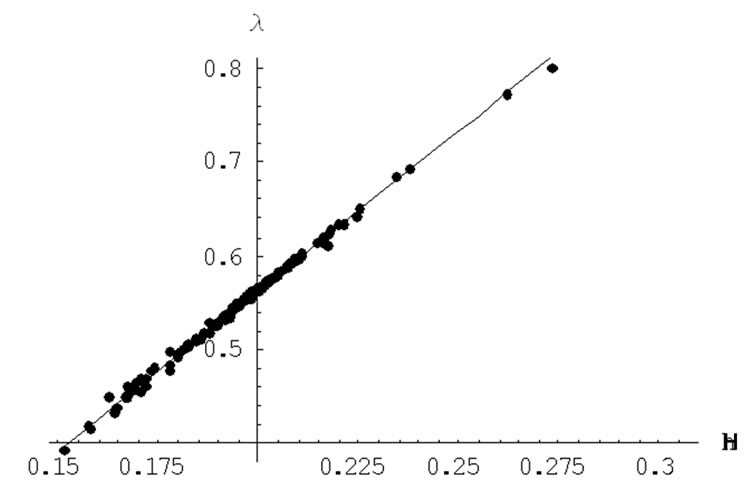
Figure 1. Graph of the raw and fitted data.
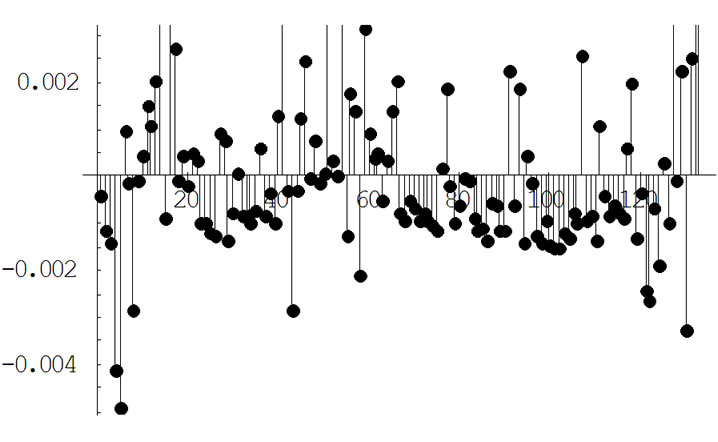
Figure 2. The distribution of the residual errors between the raw and the fitted data.
this relation, is an intrinsic relation for Hyades cluster, by which most of the properties of the cluster could be determine just from the observed data of N (say) cluster members. Of these properties are: The velocity of the cluster; the radial velocities of the cluster members; the parallaxes of the cluster members; the absolute magnitudes of the cluster member; the heliocentric coordinates of the cluster center, and the distance of the cluster. In addition to these properties, the relation could be used to obtain initial values of the vertex coordinates, which then be improved iteratively using the procedure of differential corrections. Finally, the relation provide new membership criterion of Hyades cluster and we call it the angular distance criterion.
5. References
[1] M. Yildiz, K. Yakut, H. Bakis and A. Noels, “Modeling the Components of Binaries in the Hyades: The Dependence of the Mixing-Length Parameter on Stellar Mass,” Monthly Notices of the Royal Astronomical Society, Vol. 368, No. 4, 2006, pp. 1941-1948. doi:10.1111/j.1365-2966.2006.10275.x
[2] P. A. Wayman, L. S. T. Symma and K. C. Blacwell, “Proper Motions and Radial Velocities of Hyades Stars,” Joint Publication of the Royal Greenwich Obser Vatory, 1965.
[3] R. B. Hanson, “A Study of the Motion, Membership, and Distance of the Hyades Cluster,” Astronomical Journal, Vol. 80, 1975, pp. 379-401. doi:10.1086/111753
[4] O. J. Eggen, “A Systematic Search for Members of the Hyades Supercluster. III. Near-Main-Sequence G and K Stars with Very Active Chromospheres,” Astronomical Journal, Vol. 89, 1984, pp. 1358-1365. doi:10.1086/111753
[5] J. E. Gunn, R. F. Griffin, R. E. M. Griffin and B. A. Zimmerman, “A Radial-Velocity Survey of the Hyades,” Astronomical Journal, Vol. 96, 1988, pp. 172-197. doi:10.1086/114800
[6] M. A. Sharaf, A. A. Bassuny and B. A. Korany, “An Error Controlled Method to Determine Parameteters of Moving Clusters with Application to Hyades,” Astrophysical Letter and Communications, Vol. 40, 2000, p. 39.
[7] J. H. J. de Bruije, R. Hoogerwerf and P. T. de Zeeuw, “A Hipparcos Study of the Hyades Open Cluster—Improved Colour-Absolute Magnitude and Hertzsprung-Russell Diagrams,” Astronomy and Astrophysics, Vol. 367, 2001, pp. 111-147. doi:10.1051/0004-6361:20000410
[8] M. A. C. Perryman, A. G. A. Brown and Y. A. A. Lebreton, “The Hyades: Distance, Structure, Dynamics, Age,” Astronomy and Astrophysics, Vol. 331, 1998, pp. 81-120.
[9] S. Boudreault, C. A. L. Bailer-Jones, B. Goldman, T. Henning and J. A. Caballero, “Brown Dwarfs and Very Low Mass Stars in the Praesepe Open Cluster: A Dynamically Unevolved Mass Function?” Astronomy and Astrophysics, Vol. 510, 2010, Article ID A27. doi:10.1051/0004-6361/200913011
[10] H. Poehnl and E. Paunzen, “A Statistical Method to Determine Open Cluster Metallicities,” Astronomy and Astrophysics, Vol. 514, 2010, Article ID A81.
[11] H. Schwan, “The Distance and Main Sequence of the Hyades Cluster Based on 145 Stars with Highly Accurate Proper Motions Obtained from Work on the Catalogues FK 5 and PPM,” Astronomy and Astrophysics, Vol. 243, 1991, pp. 386-400.
[12] M. A. Sharaf, “Relation between the Apparent Magnitude and the Parallax for Hyades Stars,” New Astronomy, Vol. 8, No. 7, 2003, pp. 645-653. doi:10.1016/S1384-1076(03)00052-6
[13] Z. Kopal and M. A. Sharaf, “Linear Analysis of the Light Curves of Eclipsing Variables. I. Analysis of the Fractional Loss of Light,” Astrophysics and Space Science, Vol. 70, No. 1, 1980, pp. 77-101. doi:10.1007/BF00641665
[14] W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, “Numerical Recipes in Fortran,” Cambridge University Press, Cambridge, 1992.

