Journal of Signal and Information Processing
Vol.06 No.02(2015), Article ID:56748,14 pages
10.4236/jsip.2015.62016
Effect of Diversity and Filtering on the Performance of Wavelet Packets Base Multicarrier Multicode CDMA System
Maryam M. Akho-Zahieh, Nasser Abdellatif
Department of Electrical and Computer Engineering, Applied Science Private University, Amman, Jordan
Email: maryamm@asu.edu.jo, nasser-abdellatif@asu.edu.jo, vice-presidentaa@asu.edu.jo
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 April 2015; accepted 24 May 2015; published 28 May 2015
ABSTRACT
In Wavelet Packets Based Multicarrier Multicode CDMA system, the multicode (MCD) part ensures the transmission for high speed and flexible data rate, the multicarrier (MC) part ensures the flexibility of handling multiple data rates, and wavelet packets modulation technique contributes to the mitigation of the interference problems. The CDMA system can suppress a given amount of interference. In this paper, the receiver employs suppression filter (SF) to mitigate the effect of narrow-band jammer interference and diversity techniques to reduce multiple access interference. The framework for the system and the performance evaluation are presented in terms of bit error rate (BER) over a Nakagami fading channel. Also, we investigate how the performance is influenced by various parameters, such as the number of taps of the SF, the ratio of narrow-band interference bandwidth to the spread-spectrum bandwidth, the diversity order, the fading parameter and so on. Finally, the performance of the system is compared with the performance Sinusoidal (Sin) based MC/MCD CDMA system.
Keywords:
Wavelet Packets, Multicarrier, Multicode, Diversity, Suppression Filter

1. Introduction
The Wavelet Packet (WP) Multicarrier (MC) Multicode (MCD) Code-Division Multiple-Access (CDMA) systems in [1] and [2] uses WPs as subcarrier instead of sinusoidal one. Since WPs have much lower sidelobes with negligible sidelobe energy leakage compared with sinusoid carriers, it can mitigate the problem of inter-carrier interference (ICI) and multiple access interference (MAI). Also, WPs are naturally orthogonal and well localize in both time and frequency domain, which relaxes the requirement of frequency or time guard among different user signals.
It is well known that the inherent processing gain of CDMA system will, in many cases, provide the system with a sufficient degree of narrow-band interference rejection capability. However, if the interference signal is powerful enough, the conventional receiver is ineffective in mitigating this problem. Interference suppression filter (SF) can be employed to reject the narrow-band interference. A wiener-type filter, described in [3] , employs a tapped delay line structure to first predict and then subtract out the narrow-band interference. The technique of diversity combining can provide an attractive means for improving system performance by utilizing the signal components of different uncorrelated paths.
In this paper, the WP-MC/MCD-CDMA overlayed with a narrow-band interference binary phase shift keying (BPSK) waveform is analyzed. It is shown that the system performance is improved when the receiver consists of SF combined with diversity. The performance of the system is compared with the Sinusoidal (Sin) based multicarrier multicode CDMA system denoted as Sin-MC/MCD-CDMA.
2. System Model and Description
The transceiver block diagram for the system under consideration is shown in Figure 1. The transmitter consists of two parts, multicode part and wavelet packet part, while the receiver consists of a bandpass filter (BPF), tap suppression filter, correlators (multicode and wavelet packet) and the diversity combiner. At the transmitting
side for the 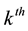 user, the bit stream
user, the bit stream  with bit duration
with bit duration 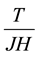 is serial-to- parallel (S/P) converted into J parallel substreams
is serial-to- parallel (S/P) converted into J parallel substreams . To reduce the inter-
. To reduce the inter-
substream interference (ISSI) resulting from the interference between the J substreams themselves, each sub-
stream with bit duration 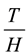 is coded by an orthogonal signal
is coded by an orthogonal signal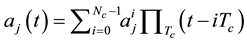 , where
, where 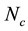 is the code length and
is the code length and 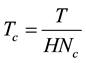 is the chip duration. To maintain orthogonality of the coding signals, the maximum number of substreams J is limited to
is the chip duration. To maintain orthogonality of the coding signals, the maximum number of substreams J is limited to . The coded substreams are added and the resulting signal
. The coded substreams are added and the resulting signal 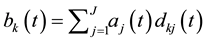 is again S/P converted into H superstreams,
is again S/P converted into H superstreams,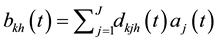 . The next step is the spreading of the H coded superstream by
. The next step is the spreading of the H coded superstream by 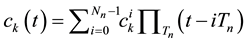 which is the pseudo-random noise (PN, processing gain) sequence of the
which is the pseudo-random noise (PN, processing gain) sequence of the 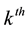 user. The length of code and chip duration are
user. The length of code and chip duration are 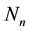 and
and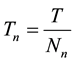 , respectively. Note that
, respectively. Note that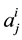 ,
, 






carrier, 




where 




where L is the number of propagation paths, 





Figure 1. Transceiver for WP-MC/MCD-CDMA employing diversity and filtering.


for the 

The receiver shown in Figure 1 is assumed to be synchronous, designed to detect the first substream of the first user’s first wavelet packet propagating via the first path. The received signal, 

where 






where 







interference band to system bandwidth
having band width 

a suppression filter which has an impulse response given by 

(




where K is the total number of users, 

The output of the filter, 




where 





is suppressed correlated AWGN and 


The output for the first correlator 

After evaluation it can be shown that

and

where 






The value of the four components







where
where





of previous data bit and current data bit, respectively. Following the definition in [5] and [6] , the partial cross-correlation functions 

Also 

The suppressed correlated AWGN component 

and the suppressed narrow-band interference 

3. Signal-to-Noise Plus Interference
To find the signal-to-noise plus interference ratio (SNIR), we need to find the desired signal power, interfer- ences, noise and jamming variances. From (8), the desired inphase signal power S is given by

To calculate the variances, it is assumed that all the interferences, noise and jamming terms are zero mean independent random variables (RV). The process of computing the variances for the different interference terms
is quite involved. Fortunately, the variances




pression filter have been computed in [1, Chapter 4]. Without loss of generality, we invoke the result in [1] and [3] for the above variances with suppression filter, which is given by
where

with 



variances it is assumed that the variation in 




Assuming that 
Also, it is evident that
And from [3]
According to this, (19) become
where 

From (15), the inphase component of the narrow jamming signal is given by
The variance can be evaluated as follows:

After certain evaluation it can be shown that

where 

given that 




where
and


4. Determination of Suppression Filter Coefficients
It is shown in [3] that the coefficients of the suppression filter can be determined using



where 




Since 


then

The 



where 


From (25) and (31), we can obtain the coefficients
5. BER and Outage Probability Performance
A common method used to measure the performance for communication systems is, the average bit error rate,

In practical applications, in order to correctly detect a transmitted signal, the error probability of the received signal must not exceed a specified value. The output SNIR



below 



5.1. Selection Diversity
For selection diversity, the overall output SNIR 

where 

Nakagami distributed with parameter





where 


5.2. Equal Gain Combining
For equal gain combining (EGC), each branch contributes equally to the overall output SNIR [8] and the decision variable can be written as

In [1] , it was found that the average BER 



5.3. Maximal Ratio Combining
Maximal Ratio Combining (MRC) is an optimum diversity combining technique, in it the diversity branches are weighted accordingly and then combined with output given as
where 





6. Results and Discussions
In this section, using the above analytical results, the BER performance and the 

6.1. Effect of Diversity
Figure 2 shows the effect of diversity and filtering on BER performance. The types of diversity used are SD, EGC and MRC. From Figure 2, it can be noted that a tremendous improvement can be achieved by using diversity and filtering. As discussed previously, MRC is an optimum diversity combining because of that MRC technique shows the best performance. Selection diversity shows the worst performance, however, one benefit of SD is its simple implementation.
Figure 2. Effect of diversity and filtering on BER performance.
Table 1. MajorSystem Parameters Used in Simulation.
6.2. Effect of Number of Filter Taps
Figure 3 shows the BER performance as a function of 






6.3. Effect of q and p
Figure 4 shows the BER performance with 3-taps DS filter as a function of q for two values of p using the three types of diversity. The system parameters are







Figure 3. Effect of number of filter taps on BER performance.
Figure 4. BER performance as function of p and q.
6.4. Effect of Diversity Order and Channel Fading
Figure 5 shows the effect of diversity order D and channel fading parameter m on BER. Three values of m are chosen, namely, 





6.5. Outage Performance
Figure 6 shows the outage performance of the system as a function of 





6.6. Performance Comparison
Figure 7 shows the comparison of our system, WP-MC/MCD-CDMA, with Sin-MC/MCD-CDMA. The systems’ parameters are


7. Conclusion
The BER and outage performance of a WP-MC/MCD system overlaying a narrow-band BPSK waveform and employing SF in the receiver has been evaluated. It is found that the performance is improved by using SF and diversity. The double-sided SF is superior to single-sided SF for the same number of total taps. The MRC has
Figure 5. Effect of diversity order D and fading parameter m.
Figure 6. Outage performance with and without SF.
Figure 7. BER performance for WP-MC/MCD-CDMA and Sin-MC/MCD-CDMA with and without SF.
better performance than SD and EGC. The performance of the system is improved by increasing the diversity order and the fading parameter. The performance of the system is improved when p increased. The system has the best BER when
Acknowledgements
The authors are grateful to Applied Science Private University, Amman, Jordan for financial support granted to cover publication fee of this research article.
References
- Akho-Zahieh, M.M. (2006) Design and Analysis of Multicarrier Multicode Wavelet Packets Based CDMA Communication Systems With Multiuser Detection. Ph.D. Dissertation, The University of Akron, Akron.
- Akho-Zahieh, M.M. and Ugweje, O.C. (2008) Diversity Performance of a Wavelet-Packet-Based Multicarrier Multicode CDMA Communication System. IEEE Transactions on Vehicular Technology, 57, 787-797.
- Wang, J.Z. (1999) On the Use of Suppression Filter for CDMA Overlay. IEEE Transactions on Vehicular Technology, 48, 405-414.
- Nakagami, N. (1960) The m-Distribution, a General Formula for Intensity Distribution of Rapid Fading. In: Hoffman, W.G., Ed., Statistical Methods in Radio Wave Propagation, Pergamon, Oxford, 3-35. http://dx.doi.org/10.1016/B978-0-08-009306-2.50005-4
- Pursley, M. (1977) Performance Evaluation for Phase-Coded Spread Spectrum Multiple-Access Communication-Part I: System Analysis. IEEE Transactions on Communications, 25, 795-799.
- Vandendorpe, L. (1995) Multitone Spread Spectrum Multiple Access Communications System in a Multipath Ricean Fading Channel. IEEE Transactions on Vehicular Technology, 44, 327-337.
- Simon, M.K. and Alouini, M.S. (2005) Digital Communication over Fading Channel. 2nd Edition, John Wiley & Sons, Hoboken.
- Proakis, J.G. (1995) Digital Communications. 3rd Edition, McGraw-Hill, New York.

































