Journal of Signal and Information Processing
Vol.3 No.1(2012), Article ID:17678,6 pages DOI:10.4236/jsip.2012.31012
A Hybrid De-Noising Method on LASCA Images of Blood Vessels
![]()
1Graduate School of Engineering, Hiroshima University, Hiroshima, Japan; 2Wuhan National Laboratory for Optoelectronics, Huazhong University of Science and Technology, Wuhan, China.
Email: {oidipous, adgle123}@gmail.com, harada@cedar.mis.hiroshima-u.ac.jp, pengchengli@mail.hust.edu.cn
Received November 8th, 2011; revised December 12th, 2011; accepted December 27th, 2011
Keywords: Brain Blood Flow; Wavelet Fusion; Hybrid Filtering; Laser Speckle Contrast Imaging
ABSTRACT
A de-noising approach is proposed that based on the combination of wiener filtering, nonlinear filtering and wavelet fusion, which de-noise the LASCA (LAser Speckle Contrast Analysis) image of blood vessels in Small Animals. The approach first performs laser spectral contrast analysis on brain blood flow in rats, get their spatial and temporal contrast images. Then, a de-noising filtering method is proposed to deal with noise in LASCA. The image restoration is achieved by applying the proposed admixture filtering, and the subjective estimation and objective estimation are given to the de-noising images. As our experimental results shown, the proposed method provides clearer subjective sense and improved to over 25 db for PSNR.
1. Introduction
Laser speckle contrast imaging (LSCI) technique is a new modality to monitoring blood flow dynamics with high spatio-temporal resolution. It records the full-field spatio-temporal characteristics of microcirculation without the need of scanning in real time [1]. Laser speckle contrast analysis (LASCA) is a non-scanning, non-invasive technique that produces 2-D map of blood flow by analyzing speckle images captured by CCD camera [2]. Our research is to develop the image quality of low frame image and make it reach the quality of high frame image by using image processing techniques. Laser speckle contrast imaging applies the 1st order spatial statistics analysis, the method of spatial statistics of Time-varying Speckle was proposed by Briers in 1980s [3]. It calculates contrast value on the local image (sub-image or statistics window), and convert into pseudo color image [4]. In fact, it can be considered as the 1st order spatial statistics analysis on speckle image, and the temporal statistics analysis is first proposed in 1976 by Ohtsubo and Asakura [5]. Serov applied this method in Laser doppler perfusion imaging and use CMOS fast imager, the sampling rate can be 9000 pps [6]. Cheng applied this in LATAC to gain the two dimension imaging of blood vessel distribution, which performs temporal statistics on each point around m frames images [7].
However, when applying LASI, the details of timevarying speckle is difficult to discriminate. It needs for spatial or temporal statistics to de-noising while preserving the details. Because the time cost in spatial LASCA and the space cost in temporal LASCA are huge, it becomes an important research objective for us that use less frames of time-varying speckle to gain higher quality imaging.
Wiener filtering is a kind of adaptive filtering, which can effectively noise restraining and protect the edge, and is widely used in image processing. However, badly in detail discriminate, it would easily cause thin line, curve, etc lost and damaged [8]. The nonlinear filters are proved to be effective in suppressing or eliminating fix-value impulse noise [9]. Moreover, nonlinear filters preserve the details and edges of an image during the process of de-noising [10]. Wavelet is an effective tool for signal restoration, which has good performance in de-noising and preserving details, but cause edge fuzzy for its soft threshold [11].
Therefore, we propose a hybrid filtering method which combines wiener filtering, order-statistic filtering and wavelet fusion, for de-noising of LASCA images. This approach first performs wiener filtering, add nonlinear filtering with the result, change the luminance; Meanwhile, makes wavelet transform on the noisy image, and via inverse wavelet transform. Finally, the result is the fusion of wavelet and those two. The experimental results show that the hybrid filtering has better performance than each single filtering, which de-noising while preserve the edge and other details of images.
2. Method
2.1. Spatial and Temporal LASCA
The laser speckle contrast analysis can be performed based on spatial statistics and temporal statistics. The spatial LASCA performs speckle contrast calculation in the spatial domain using a spatial window. It achieves high temporal resolution with the loss of spatial resolution, impeding its application on monitoring blood flow changes in small vessels. The temporal LASCA method, which is based on temporal statistics, computes speckle contrast images using a sequence of speckle images acquired along a few time points instead of using a spatial window. It preserves the original spatial resolution by sacrificing the temporal resolution, making it inappropriate in applications where video frame rate visualization of blood flow is required.
2.2. Wiener, Nonlinear (Order-Statistic) and Wavelet Filtering
The inverse filtering is a restoration technique for deconvolution, i.e., when the image is blurred by a known lowpass filter, it is possible to recover the image by inverse filtering or generalized inverse filtering. However, inverse filtering is very sensitive to additive noise. The approach of reducing one degradation at a time allows us to develop a restoration algorithm for each type of degradation and simply combine them. The Wiener filtering executes an optimal tradeoff between inverse filtering and noise smoothing. It removes the additive noise and inverts the blurring simultaneously. The Wiener filtering is optimal in terms of the mean square error. In other words, it minimizes the overall mean square error in the process of inverse filtering and noise smoothing. The Wiener filtering is a linear estimation of the original image. The approach is based on a stochastic framework [12].
A nonlinear filter is a signal-processing device whose output is not a linear function of its input. Terminology concerning the filtering problem may refer to the time domain (state space) showing of the signal or to the frequency domain representation of the signal. When referring to filters with adjectives such as “bandpass, highpass, and lowpass” one has in mind the frequency domain. When resorting to terms like “additive noise”, one has in mind the time domain, since the noise that is to be added to the signal is added in the state space representation of the signal. The state space representation is more general and is used for the advanced formulation of the filtering problem as a mathematical problem in probability and statistics of stochastic processes [12].
The wavelet filter is good at removing gaussian-type noise, while it can leave some kind of photon noise (very hot pixels for example). Thus an option is provided in the form of an optional adaptive median filter. This filter will detect pixels that differ from their context by more than a given multiple of the neighborhood’s standard deviation. If marked as outlying, the pixel value is replaced by the median value of the neighborhood. A suggested default value is 1.6 * sd. The idea behind this filter is that if an adequate sampling was chosen upon acquisition, no such outlying (extreme value) pixels should be found [12].
2.3. Proposed Hybrid De-Noising Method
Based on the comparison of several filtering methods discussed above, considering their advantages, we put forward a hybrid de-noising method oriented for LASCA images, which combined with wiener, nonlinear and wavelet filtering.
The process is shown below:
1) Apply spatial statistical analysis or temporal statistical analysis on LASI (time-varying speckle) images, to gain spatial LASCA and temporal LASCA for small number of frames. They are all noising images.
2) Perform wiener filtering, nonlinear filtering (order-statistic filtering) and luminance adjust on the noisy image.
3) Meanwile, perform wavelet de-noising on the same image.
4) Fusion those two midterm results, in order to get the final de-noising image.
The framework is shown in Figure 1.
3. Experiments and Discussions
3.1. LSCI System
The schematic setup for the experiment is shown in Figure 2. A rat was anesthetized and fixed in a stereotaxic instrument. An approximately 5.0 × 5.0-mm cranial window with intact dura was formed by removing the skull overlying one side of the parietal cortex with a high speed dental drill (Fine Science Tools, USA) under constant saline cooling. A beam of He-Ne laser (Melles Griot, America; 632.8 nm and 15 mW) was expanded and collimated to illuminate the cranial window at about 30-deg incidence. 30 frames of statistically independent laser speckle images were acquired by a 12-bit chargecoupled device (CCD) camera (PixelFly QE, PCO Computer, Germany; pixel size = 6.45 × 6.45 μm) attached to a microscope (Z16 APO, Leica, Germany; working distance 97 mm)for data processing. The CCD exposure duration was 20 ms and the frame interval time is approximately 87 ms. The system magnification is adjusted to 3.15×, and the aperture diaphragm is well controlled to ensure the average speckle size of the images to be approximately two pixels. A variable attenuator was used in the light path to ensure the light intensity within the dynamic range of the CCD camera. The whole setup was

Figure 1. Framework of proposed hybrid de-noising method.

Figure 2. Scheme of laser speckle contrast imaging system.
placed on a vibration-isolator table (VH3036W, Newport). System constituted by laser light source, microscope, CCD camera and computer.
The experimental setup for laser speckle contrast imaging is very simple. Diverging laser light illuminates the object under investigation, which is imaged by a CCD camera (or equivalent). The image is captured by a frame grabber (or equivalent) and the data passed to a personal computer for processing by custom software.
3.2. Evaluate Criterion
Because the Temporal Contrast Analysis (100 Frames) has a fine performance, in our research, it is considered as the base image, which is used in objective estimations —MSE, SNR and PSNR.
The above three objective measurements are selected and used for our research study. Definition: x(m,n) denotes the base image, x^(m,n) denotes the de-noising image. M and N are number of pixels in row and column directions, respectively.
3.2.1. Mean Square Error (MSE)
The simplest of image quality measurement is Mean Square Error (MSE). In statistics, the MSE of an estimator is one of many ways to quantify the difference between values implied by an estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or quadratic loss. MSE measures the average of the squares of the “errors.” The error is the amount by which the value implied by the estimator differs from the quantity to be estimated. The large value of MSE means that image is poor quality. MSE is defined as follow:
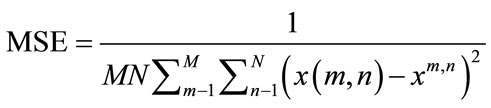
An MSE of zero, meaning that the target image is the ideal, but is practically never possible. In our case, the smaller the MSE value, the denoising performance is better.
3.2.2. Signal to Noise Ratio (SNR)
Signal-to-noise ratio (often abbreviated SNR or S/N) is a measure used in science and engineering to quantify how much a signal has been corrupted by noise. It is defined as the ratio of signal power to the noise power corrupting the signal. A ratio higher than 1:1 indicates more signal than noise.
SNR is defined as follow:

where P is average power.
3.2.3. Peak Signal to Noise Ratio (PSNR)
The phrase peak signal-to-noise ratio, often abbreviated PSNR, is an engineering term for the ratio between the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of its representation.
The small value of Peak to Noise Ratio (PSNR) means that image is poor quality. PSNR is defined as follow:
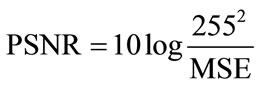
The PSNR is most commonly used as a measure of quality of reconstruction of lossy compression codecs (e.g., for image compression). The signal in this case is the original data, and the noise is the error introduced by compression. When comparing compression codecs it is used as an approximation to human perception of reconstruction quality, therefore in some cases one reconstruction may appear to be closer to the original than another, even though it has a lower PSNR (a higher PSNR would normally indicate that the reconstruction is of higher quality).
As a part of estimation, we do in this way: mainly compare the subjective performance between the base image and our hybrid de-noising image. Also, we provide the performance of 3 single de-noising methods we apply, in order to ensure the effectiveness of our hybrid method. 2 former researchers’ works (Med and Linear Filters) are added in our comparison at last.
3.3. Experimental Results and Analysis of Spatial LASCA Image De-Noising
We show the results of each de-noising filter in Figure 3 from original (noisy LASCA image), our proposed filter to each single filter, also, we add other researcher’s methods such as Linear de-noising and so on. From the widely compare, it is firmly shown that, our hybrid denoising have the best objective performance. Moreover, Table 1 shows the specific data of objective estimations.
3.4. Experimental Results and Analysis of Temporal LASCA Image De-Noising
We choose sampling frame parameter as 8 frames in temporal LASCA. Similarly with Spatial LASCA, in Temporal experiment, the same comparison has been down. The subjective estimation results are shown in Figure 4, the objective estimation results are shown in Table 2.
3.5. Experimental Results and Analysis of Proposed Method under Different Frame Parameters
In this section, the performance of our proposed de-
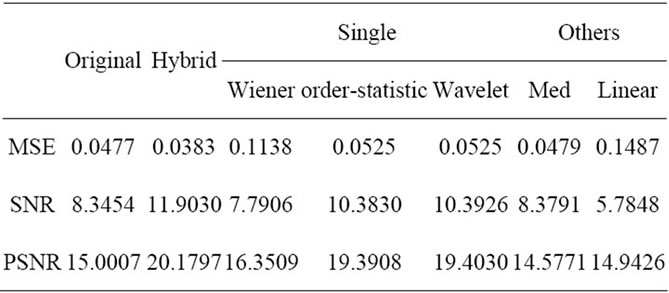
Table 1. Estimation of de-noising (for spatial LASCA).

Table 2. Estimation of de-noising (for temporal LASCA).
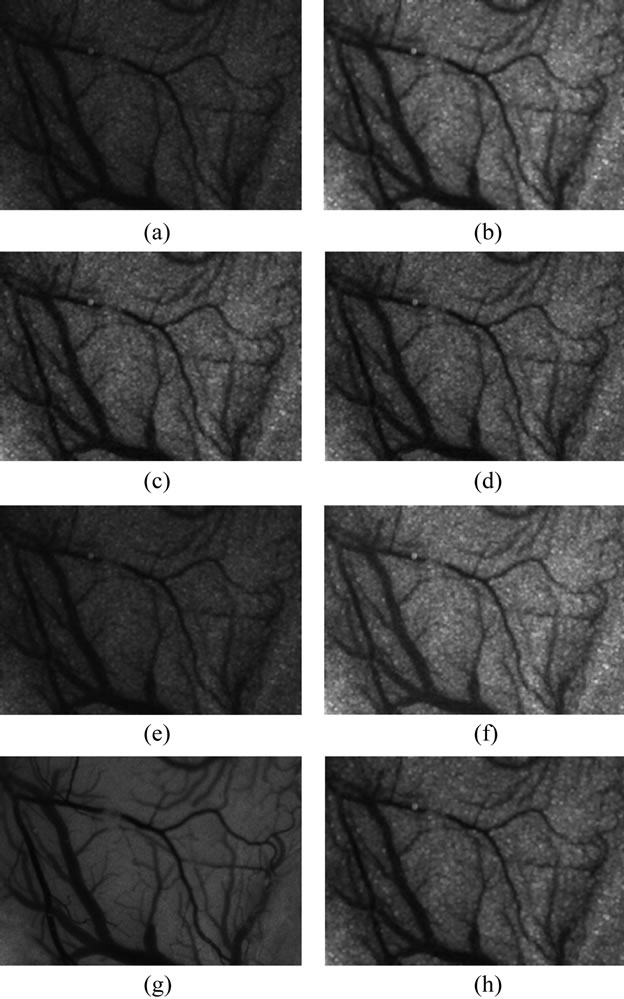
Figure 3. (a) Noisy LASCA image (Spatial); (b) Wiener denoising; (c) Order-statistic de-noising; (d) Wavelet denoising; (e) Med de-noising; (f) Linear de-noising; (g) Base image; (h) Proposed Hybrid de-noising.
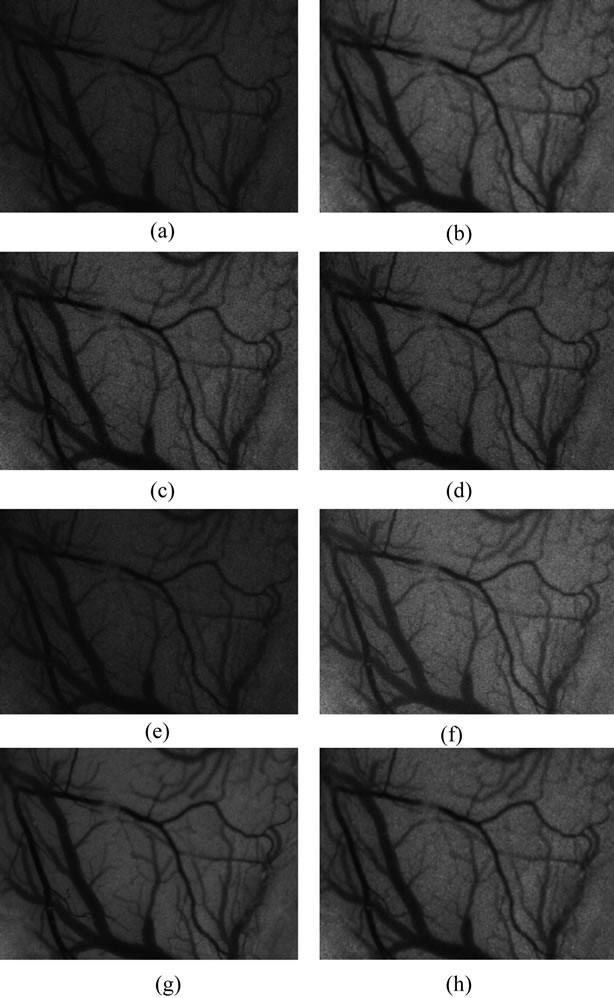
Figure 4. (a) Noisy LASCA (temporal 8 frames); (b) Wiener de-noising; (c) Order-statistic de-noising; (d) Wavelet denoising; (e) Med de-noising; (f) Linear de-noising; (g) Base image; (h) Proposed hybrid de-noising.
noising method under different contrast frame parameters is provided and discussed.
For 6 groups of noisy Temporal LASCA images (contrast parameter varies from 5 frames to 40 frames), our de-noising method is proposed, the experimental results are shown in Figure 5, the objective estimation results are shown in Table 3.
From the table above, the graphical result can be generated as Figure 6 shown. The horizontal vector shows the value of frame while the vertical vector shows the dB value of each objective estimation factor.
From Figure 6 and Table 3, it is clear shown that, while the contrast parameter increases, the corresponding MSE value changes from 0.0056 to 0.02, and has not obvious variation. The SNR value changes from 13.7 to 13.96, also not much variation. The PSNR value increases from the range of 5 to 10 frame, however, when bigger than 10 frame, the changing becomes tiny.
3.6. Discussion
Consider the results of Spatial and Temporal LASCA
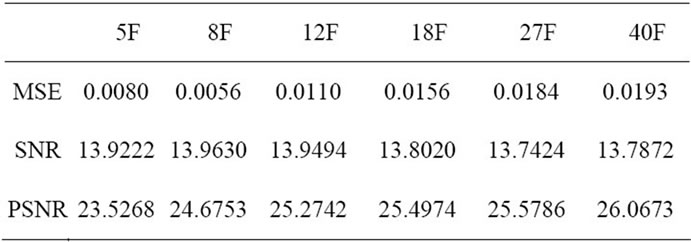
Table 3. De-noising results of proposed method under different frames.
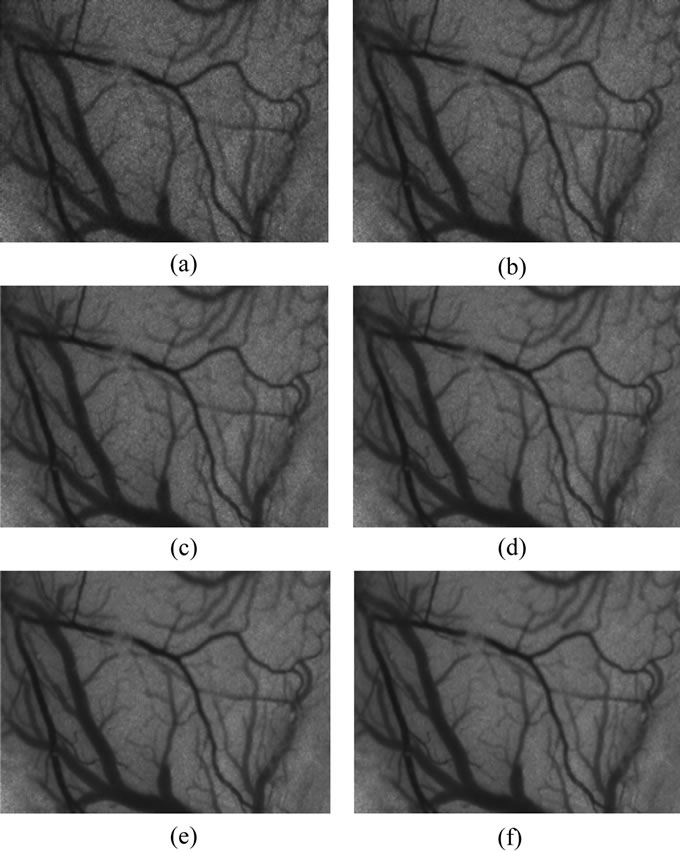
Figure 5. De-noising results of proposed method under (a) 5 frames; (b) 8 frames; (c) 12 frames; (d) 18 frames; (e) 27 frames; (f) 40 frames temporal LASCA.
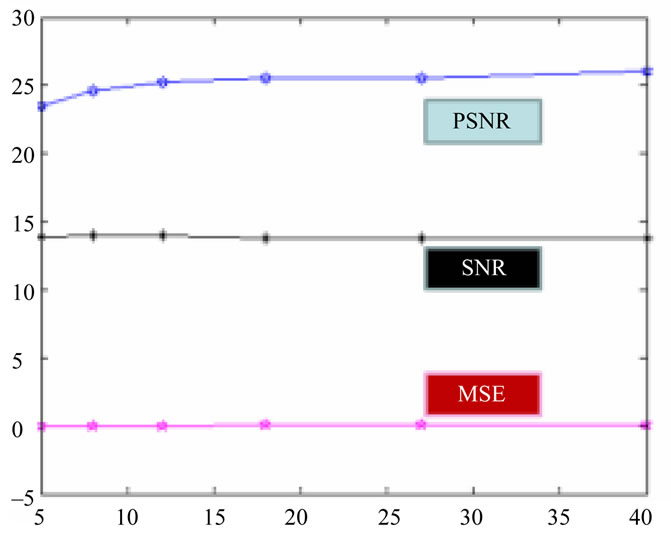
Figure 6. Plot result.
images de-noising, our proposed hybrid method has good subjective performance around all methods we provide (shown in Figure 3 and Figure 4). Meanwhile, our method performs the best in MSE, SNR and PSNR estimation, shown in TABLE I and TABLE II (That means MSE has the least value and SNR/PSNR have the largest value).
From the performance under different contrast parameter, we can claim that the number of frames does NOT affect our method’s performance much. The de-noising under small number of contrast can be close to the large number of contrast image (such as 100 Frames in our research). The effectiveness of our method is proved.
4. Conclusions
This paper proposes a hybrid filtering for LASCA in denoising of medical images. Regrouping Wiener filtering, order-statistic filtering, Wavelet de-noising and fusion technology, the laser speckle imaging based on spatial contrast or temporal contrast has been down, and the denoising is performed. From the experiment, we can conclude that 1) The proposed hybrid filtering for spatial and less frame contrast image (5 F, 8 F, etc) has high value of PSNR and good subjective performance.
2) The hybrid filtering absorbs all the benefits of each filtering.
3) From the results, both subjective and objective performance, the hybrid filtering is the best or one of the best. Therefore, it is considered that it has better performance than other single filtering.
One of our research motivations is that doctors find it delay when they using Temporal LASCA to do real time diagnosis. The high quality LASCA result (such as 100 F) would costs more time, while the low quality (such as Spatial or 5 F) can not provide good image. Our attempt by using denoising method in image processing filed can improve the image quality in fewer time than performing high frames LASCA. Our hybrid denoising method absorbs the benefits of single denoising method while the time consumption doesn’t change a lot.
5. Acknowledgements
All the anonymous reviewers are gratefully acknowledged for their carefully considered feedback and valuable comments. The modification is due to their effort.
REFERENCES
- Q. Liu, S. B. Zhou, Z. H. Zhang and Q.-M. Luo, “Application of Laser Speckle Imaging: Monitoring Changes of Vessels in Photodynamic Therapy,” Chinese Journal of Lasers, Vol. 32, No. 6, 2005, pp. 869-872.
- S. S. Liu, P. C. Li and Q. M. Luo, “Fast Blood Flow Visualization of High-Resolution Laser Speckle Imaging Data Using Graphics Processing Unit,” Optics Express, Vol. 16, No. 19, 2008, pp. 14321-14329. doi:10.1364/OE.16.014321
- J. D. Briers, “Optical Filtering Techniques to Enhance Speckle Contrast Variations in Single-Exposure Laser Speckle Photography,” Optik, Vol. 63, 1983, pp. 265-276.
- J. D. Briers and S. Webster, “Laser Speckle Contrast Analysis (LASCA): A Non-Scanning, Full-Field Technique for Monitoring Capillary Blood Flow,” Journal of Biomedical Optics, Vol. 1, No. 2, 1996, pp. 174-179. doi:10.1117/12.231359
- J. Ohtsubo and T. Asakura, “Velocity Measurement of a Diffuse Object by Using Time-Varying Speckles,” Optical and Quantum Electronics, Vol. 8, No. 6, 1976, pp. 523-529. doi:10.1007/BF00620143
- A. Serov, W. Steenbergen and F. D. Mul, “Laser Doppler Perfusion with a Complimentary Metal Oxide Semiconductor Image Sensor,” Optics Letters, Vol. 27, No. 5, 2002, pp. 300-302. doi:10.1364/OL.27.000300
- H. Y. Cheng, Q. M. Luo, S. Q. Zeng, et al., “Modified Laser Speckle Imaging Method with Improved Spatial Resolution,” Journal of Biomedical Optics, Vol. 8, No. 3, 2003, pp. 559-564. doi:10.1117/1.1578089
- H.-M. Zhang, X. P. Chen and Y. J. Zhang, “Improved Wiener Filter Algorithm for Image Restoration,” Journal of Chongqing University of Technology (Natural Science), Vol. 24, No. 7, 2010, pp. 76-80.
- S. M. Mansor Roomi, et al., “Impulse Noise Detection and Removal,” ICGST-GVIP Journal, Vol. 7, No. 2, 2007, pp. 51-56.
- K. Somasundaram and P. Shanmugavadivu, “Impulsive Noise Detection by Second Order Differential Image and Noise Removal Using Nearest Neighborhood Filter,” International Journal of Electronics and Communications, Vol. 62, No. 6, 2007, pp. 472-477.
- S. P. Ghael, A. M. Sayeed and R. G. Baraniuk, “Improved Wavelet Denoising via Empirical Wiener Filtering,” Proceedings of SPIE, San Diego, July 1997, pp. 389-399.
- R. C. Gonzalez and R. E. Woods, “Digital Image Processing,” 3rd Edition, Prentice Hall, Englewood Cliffs, 2008.

