International Journal of Geosciences
Vol.07 No.04(2016), Article ID:66088,17 pages
10.4236/ijg.2016.74046
Imaging Rock Density Distribution beneath Liwa Fracture Zone in the Southern Part of the Great Sumatran Fault System, Indonesia
Djedi S. Widarto1*, Tedi Yudistira2, Jun-Ichi Nishida3, Ikuo Katsura4, Eddy Z. Gaffar5, Susumu Nishimura4
1Upstream Technology Center, PT Pertamina (Persero), Jakarta, Indonesia
2Department of Geophysical Engineering, Bandung Institute of Technology, Bandung, Indonesia
3Faculty of Literary, Ohtani University, Kyoto, Japan
4Kyoto Institute of Natural History, Kyoto, Japan
5Research Centre for Geotechnology―LIPI, Bandung, Indonesia

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 March 2016; accepted 25 April 2016; published 28 April 2016
ABSTRACT
We have imaged rock density distribution beneath Liwa fracture zone in the southern part of the the Sumatran Fault Zone by modelling and inverting Bouguer gravity data in two-and three-di- mensional environments, respectively. The purpose of this study is aimed to figure out the subsur- face distribution of rock densities associated with subsurface basement structure representing the evidence of trans-tensional tectonic product in the SF. In the gravity modeling, to eliminate distortions to the measured gravity values before modelling and inverting the data, Bouguer anomalies obtained in field measurements are reduced to the horizontal plane of z = +800 m as a representation of the average elevation in Liwa. For the inversion, we used algorithm implementing depth-and minimum volume weighting parameters in order to obtain a smooth model with better vertical resolution. The two-dimensional models show clearly surface topography of the basement rocks and the presence of normal faults. The reduced Bouguer anomaly of +800 m elevation shows the presence of structural lineaments extending primarily in a northwest-southeast direction, parallel to Sumatran Fault Zone and older graben faults showing a negative flower structure. From the three-dimensional inversion, the model illustrates an increase of density contrast, lower values being found near the surface and higher values in the deeper parts. The lower density contrast of 0.15 to 0.3 g/cm3 found in the rock groups at depths of 2 km and less is characteristic of relatively homogeneous and poorly compacted rocks. Rocks with moderate to high density contrast (>1.0 g/cm3) are recognized at depths of over 2 km. This model suggests a change of basement morphology as a function of depth, and delineates structural lineaments extending in northwest-southeast direction. This study supports the previous thought that Liwa area is underlain by graben structures, formed by trans-tensional tectonic events. Higher-density Tertiary volcanic breccia and lower-density Quaternary volcanic products of the Ranau Formation form the basement rocks and the overlying younger sediments, respectively.
Keywords:
Gravity Imaging, Rock Density, Fracture Zone, 2D Modeling, 3D Inversion, Density Contrast

1. Introduction
The gravity method is one of geophysical prospecting methods that are widely used in the exploration of hydrocarbons [1] - [3] , geothermal [4] - [6] , minerals [7] [8] , and environmental and engineering problems [9] [10] , as well as the study of the Earth’s crust structures [11] [12] . The method is based on the existence of rock density contrast at the subsurface that can be measured either directly or indirectly in the form of gravity anomaly. This contrast could characterize the presence of specific geological features, such as faults or layer boundary and the materials that constitute the layer, including the presence of fluids within the layer. Poorly compacted rocks generally show a lower density value than well-compacted rocks. In general, their differences in density vary between 0.3 and 0.7 g/cm3 [13] . In relation with those mentioned, we carried out detailed gravity survey in the Liwa fracture zone of the southern segment of the Sumatran Fault Zone (hereafter, SF). This work is aimed to characterize the image of subsurface structures beneath an intensively fractured zone. In this respect, this survey can also be used to provide subsurface features related to the faults movement or in evaluating the potential of natural resources. This paper will discuss the results of gravity survey in the Liwa fracture zone with reference to the images obtained by two-dimensional (2-D) modelling and three-dimensional (3-D) inversion of gravity data. The images obtained in the modeling were then interpreted to figure out the subsurface basement structures associated with trans-tensional tectonic developed in the study area. In this work, 3-D inversion of gravity data is performed with the purpose of obtaining detailed image of rock density distribution at the shallow depths of up to 2 km with 200 m elevation levels.
2. Geology and Seismicity
Liwa area is well-known as a depression zone situated in the southern part of Sumatra Island, where the SF and magmatic belt run parallel to the Sunda Trough from the back-arc basin of the Andaman Sea to the Sunda Strait extensional fault zone. The SF is a right lateral strike-slip fault caused by the oblique subduction of the Indian Ocean tectonic plate. With the aid of satellite images, Bellier and Sébrier [14] [15] have calculated the rate of displacement at 23 ± 3 mm/year in the north and 6 ± 4 mm/year in the south. Figure 1 shows the segmentation of the SF along the Sumatra Island as based on the study carried out by Sieh and Natawidjaja [16] . They described that the Liwa area, which is situated approximately 25 km to the southeast of Lake Ranau, is produced by trans-tensional depression tectonic processes. Liwa area is morphologically divided into three units, i.e. Liwa plateau, undulating hills, and rugged-terrain hills units. The plateau is a valley extending in a west-east direction at an altitude of 700 - 800 m, occupying nearly half of the surveyed area.
Geological setting of Liwa and the surrounding areas have been studied and reported by Amin et al. [17] and Gafoer et al. [18] . The Liwa plateau consists primarily of volcanic tuff and andesite, also known as Liwa tuff, and alluvial sediments. Undulating hills with an elevation of 100 m above sea level cover almost 30% of the surveyed area. This unit occupies the southern part of Liwa area and consists of Miocene lava, laharic breccia, and dacitic tuffs. Rugged-terrain hills varying between 1000 and 1600 m in height are present in the south, southeast and eastern part of the study area. In the northernmost parts, this unit has an elevation of 1250 - 1400 m. Upper Miocene laharic breccia and dacitic tuffs dominate the unit, while Quaternary lava and volcanic breccia occupy its topmost parts.
Through the study of Landsat images, Suwijanto et al. [19] determined the boundaries of rock unit distribution and structural lineaments of the area as shown in Figure 2. The most commonly found geological features in Liwa area are strike-slip and normal faults. The strike-slip faults generally follow a northwest-southeast trend
Figure 1. Geometric and structural details of the Great Sumatran Fault Zone (after Sieh and Natawidjaja, 2000). SF, WAF, IFZ and MFZ denote the Sumatran Fault, Andaman Fault Zone, Investigator Fault Zone, and Mentawai Fault Zone, respectively. The dashed-grey lines with numeric are the depth of subduction slab. The rectangle, namely Liwa, is the study area as depicted in Figure 2.
Figure 2. Simplified surface geologic map and structural lineaments in Liwa and surrounding regions according to studies on Landsat images. Quaternary volcanic rocks are mainly composed of Ranau Formation. Mt. Pesagi was formed and surrounded by a caldera collapsed-structure (after Suwijanto et al., 1996).
in line with the primary direction of the SF. On the other hand, the normal faults are mostly extended along northeast-to-southwest directions. Collapsed- or graben-like structures and remnants of old volcanic craters have been found in several locations. All of those structures are part of the southernmost segment of the SF. The presence of the faults can be detected in Landsat images by examining the displacement of river valleys both in lateral and in vertical directions.
Volcanic and geothermal activities are present in considerable amounts, as indicated by the presence of Lake Ranau in the north and the Suwoh geothermal field in the south. The area is also a strong compression zone where major shallow earthquakes have been recorded in 1913, 1933, and 1994. The destructive earthquake in February 15, 1994 (Ms = 7.2, NEIC-USGS; Mw = 6.9, Harvard-CMTS; mb = 6.8, EMSC), with the depth of the source calculated at 23 km, resulted in the loss of over 200 lives [20] . The greatest damage occurred extending as a long narrow zone that coincides with the main strike of the SF. The epicenter of the 1933 earthquake (Ms = 7.5) almost coincides with that of the 1994 earthquake [21] . Destructive earthquakes are common in the vicinity of the SF, but higher seismicity levels are found in fore-arc and plate boundary regions. This phenomenon of high seismicity may be related not only to the oblique convergence of the Indian Ocean plate but also with fore- arc deformation [20] .
3. Acquisition and Processing
Acquisition of gravity data was conducted with a LaCoste & Romberg Series G-804 gravimeter. The gravity value for each measurement point was determined with reference to the DG-0 gravity value of 977,976.38 mGal. This DG-0 gravity value was first determined by Evans and Greenwood [22] as 977991.05 mGal in the Potsdam system. This value was subsequently converted into the IGSN’71 system.
In order to conduct field measurements, we established a local base station called BSLIWA, located in the inner courtyard of the Liwa Observatory Station. All gravity measurement values obtained use BSLIWA as a local reference point. Figure 3 shows the locations of 227 gravity measurement points on the Liwa area. All the measurement points are located next to roads accessible to vehicles. The gravity value at BSLIWA, 977,930.15 mGal, was determined with reference to DG-0 in Bandung of Java island and the Branti gravity station at southern part of Sumatra. In general, the measurement points were distributed over the Liwa valley, while some were located along the Liwa-Krui and Liwa-Ranau roads.
Figure 3. Map of gravity measurement locations in 2000 (solid circles) and 2001 (open circles). The inner rectangle delineates the effective limits for the extrapolation of a Bouguer anomaly map and is smaller area than that of the geologic map as depicted in Figure 2.
Gravity data measurements were conducted by a closed-loop method. The initial and final measurements were taken at the same BSLIWA point within the same day. In this study, the difference between the results acquired in the initial and final measurements did not exceed 0.1 mGal. The measured gravity values were converted according to the scale factor readings on the G-804 gravimeter. After appropriate corrections to compensate for the effects of tides and drift, the gravity values were determined through the process described in the following pages.
A topographic map of 1:50,000-scale was used for the field map for the gravity measurements. The precise latitudes and longitudes of the measurement points were determined with a Garmin III+ GPS receiver using the Indonesia ’74 datum system. The elevation of the measurement points were determined with the aid of a Wallace-Tiernan altimeter, controlled with reference to known triangulation points or the sea level. Differences caused by changes in air pressure were corrected according to a record of barometric pressure chart obtained with an automatic analog barograph at BSLIWA. Even with this correction it is impossible to completely eradicate all errors associated with local variations in air conditions at the measurement points. Altitude measurements taken at the same location on different days indicate a maximum margin of error of 5 m.
Generally, the complete Bouguer anomaly value 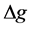 was calculated by the following equation:
was calculated by the following equation:
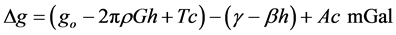 (1)
(1)
where go is the measured gravity value in mGal, h is the elevation in meters, ρ is the specific gravity of the subsurface rocks in g/cm3, G is the gravity constant, Tc represents terrain corrections in mGal, γ is the normal gravity value, β is the vertical gravity gradient, and Ac represents the atmospheric correction. Due to the proximity of the Liwa region to the equator, a vertical gradient value of 0.3088 mGal/m was used in the determination of anomalies [23] . Terrain corrections were made with Hammer’s method [24] for the inner zone. The normal gravity value was determined according to the International Gravity Formula 1967 [25] as;
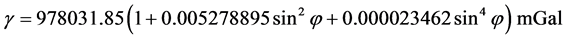 (2)
(2)
where φ is the latitude of the gravity measurement point. The atmospheric correction was then determined according to the formula Ac = 0.87 − 0.0000965 h mGal, where h is elevation in meters.
Determination of average density of rocks at the subsurface is needed in analyzing the gravity anomaly. The method to ascertain the average density is given by transforming Equation (1) into;
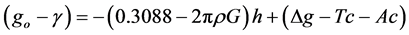 (3)
(3)
Since the value of 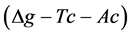 is too small, and hence it is negligible, we can regard the variable as noise. The value of
is too small, and hence it is negligible, we can regard the variable as noise. The value of 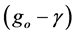 is proportional to h. If we examine the slope of the plotted gravity measurement results with the least-squares method, the slope would be proportional to the value of
is proportional to h. If we examine the slope of the plotted gravity measurement results with the least-squares method, the slope would be proportional to the value of 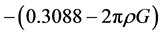 so that the
so that the
average density of the rocks in the Liwa area can be directly determined. Figure 4 displays the relation between
Figure 4. Determination of average rock density in Liwa area on the basis of the relation between (go ? γ) and h. Open circles indicate measured gravity values and the solid line is the gradient obtained by the least-squares method to yield an average density of 2.6 g/cm3.
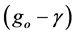 and elevations h for each gravity measurement point in Liwa. The relation shows that the average rock
and elevations h for each gravity measurement point in Liwa. The relation shows that the average rock
density in Liwa is 2.60 g/cm3. This value is relatively low compared to the average density of the Earth’s crust, which is 2.67 g/cm3. Nishimura et al. [26] reported that the value of rock density in the southernmost of Sumatra is 2.64 g/cm3. They explained that the density is a result of the fact that the basement rocks of Sumatra are mostly composed of gneiss and granite. On the other hand, the low value of average rock density in Liwa is assumed to be influenced by tuffaceous sandstones of the Ranau Formation, which is widely distributed in the area.
4. Modelling and Inversion
In this study, we applied both of 2-D forward and 3-D inversion modellings of the gravity data. The 2-D modelling as based on the well-known Talwani et al.’s [27] algorithm is carried out primarily to obtain an image of vertical contrast of rock densities. To do this, we applied the method to two sections that cross structural lineaments inferred as faults. In the meanwhile, 3-D inversion of gravity data is conducted in order to understand the distribution of rock densities in both vertical and lateral variations. Discussion of the 3-D inversion in such more detail will be given in the following.
Inversion of potential field data, such as gravity and geomagnetic, is facing with the problem of non-unique solutions and ambiguity, not to mention the low vertical resolution of the resulting model. In order to overcome those difficulties, it is necessary to provide additional inputs of data or information, for example by including initial information about anomaly sources obtained from other geological or geophysical data. In general, the accuracy of the resulting solution in approximating the actual sources of the anomaly would depend on the quality of this additional information. As such, there is a need to label this additional information with an index of reliability or weighting factors.
The problem of low vertical resolution in potential field inversion is related to the nature of the solution obtained from the inversion method. Without the aid of any additional information, the process would provide a low-resolution image of the anomaly sources at the depth. Shallow sources would become too prominent while deeper sources would either fail to show up in the model or be mapped at shallower depths. This issue of poor vertical resolution has been satisfactorily explained by several researchers, particularly Li and Oldenburg [28] and Boulanger and Chouteau [29] . They explained that the kernel matrix, which in this case maps the model against the data, is seen as a weighting factor in determining rock density or magnetization.
Several methods have been proposed to deal with this lack of vertical resolution. These include minimizing certain objective functions such as by minimizing the volume of the anomaly source or by maximizing the compactness of the rock material [30] . The model obtained in this way would give greater focus to the center area of the source. Guillen and Menichetti [31] and Barbosa and Silva [32] utilized a weighting factor in the form of moment of inertia relative to the gravity center or to a certain axis. Li and Oldenburg [28] [33] use a depth-weighting of the model parameters in conjunction with a minimization of the spatial variation in the physical model parameters, so that the resulting model would be smoother and possess better vertical resolution. Alternatively, Fedi and Rapolla [34] inverted 3-D data groups at several elevation levels to overcome the poor vertical resolution. Boulanger and Chouteau [29] combined several constraints and evaluate their effects on the resulting model.
A detailed discussion on the implementation of those two constraints or weighting methods, i.e. depth weighting and minimum volume parameters, on the inversion of gravity data follows in the next section. Subsurface conditions are approximated by a set of three-dimensional prisms, each of a fixed density value. In this approach the relation between the data and the physical parameter (in this case, rock density) would form a linear equation. The equation is solved by the method of weighted least-squares, minimizing the objective functions of data misfit and model norm.
4.1. Formulation of the Inversion
If the source is treated as a set of 3-D prisms, assuming that there are M prisms evaluated at N observation points (see Figure 5), then the total gravity field at the I-th point, gi, would be the sum of the fields generated by each prism such that it can be described by the following equation:
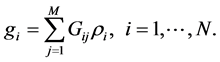 (4)
(4)
Figure 5. The arrangement of prisms in a 3-D model as an approximation of subsurface conditions.
where ri is the density value at the i-th block and G is as kernel defined in transfer function from density to gravity. In a matrix notation, Equation (4) can be written as
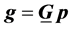 (5)
(5)
where g is the vector of a data of size N, p is the physical parameter vector of rock density of size M, and 
4.2. Inversion Solution
The solution seeks to determine the distribution of estimated rock density. The general statement of the solution to Equation (5) can be described by the following equation:

where 


where p0 is the initial model and gobs is the observed data vector.
Equation (7) is obtained by minimizing the objective function of data misfit,
(7) is applied without modification, the resulting model would be concentrated near the surface because the gravity data does not include a vertical resolution to base the model on and there is a lack of additional constraints or information that can be used to eliminate the problem. To handle this complication, the minimization must include not only data misfit in the objective function but also a model norm

where Wm is a diagonal matrix where the elements are the product of the multiplication of depth weighting with minimum volume that gives a proper weighting to the density value of the rocks in each block. The minimization of objective function in Equation (8) yields the following solution:

The model is produced through an iterative process where the weighting matrix Wm is modified for each iteration, resulting in the equation:

where k is the number of steps in the iteration.
4.3. Depth and Volume Weightings
Due to the fact that gravity fields are attenuated by distance, the value of Gij for blocks at greater depths would be greater than that for blocks at shallow depths. This reduces the model’s sensitivity for blocks in greater depths, causing the solution to be concentrated near the surface. To counteract this attenuation property, the kernel matrix must be modified with a weighting factor to provide a relatively more even distribution of chance for all blocks. The depth weighting factor wz is formulated according to Li and Oldenburg [28] as

where zj is the depth of the j-th block, e is a constant of appropriately small value, and b is a constant within the value range of [0.5 - 1.0] [29] .
Minimum volume weighting is applied with the view of obtaining a sharper image of the anomaly source. In other words, the volume of the anomaly is compacted so that the rock density values would not be diffused to distant blocks. The minimum volume weighting wv (compactness) is formulated according to Last and Kubik [30] as

or, alternatively as another formula from Boulanger and Chateau [29] ,

where a is a constant calculated to give the minimum-volume weighting a desired level of influence on the resulting model.
5. Results and Discussion
5.1. Complete Bouguer Anomaly
Bouguer anomaly values were calculated under the assumptions that the value of the vertical gravity gradient is 0.3088 mGal/m and the average rock density is 2.60 g/cm3. Figure 6 shows a complete Bouguer anomaly map
Figure 6. Complete Bouguer anomaly contour map for the gravity measurement points in the area as delineated in Figure 3. The Bouguer anomaly values are plotted on the actual topography with a contour interval of 2 mGal. Solid circles denote gravity measurement points.
extrapolated from the gravity measurement points in the area delineated by the rectangle in Figure 3. Due to the random distribution of the measurement points and the need to avoid exaggerated extrapolation, the gravity data from the proximity of Krui and Ranau Lake were not included in the compilation of the Bouguer anomaly map.
The map shows that the highest anomalous zone, >52 mGal, is found in the southwestern part of Liwa. This high anomaly is thought to be correlated to the Tertiary andesite and volcanic basalts of the rugged-terrain hills along the SF. On the other hand, the low anomaly value in the northeastern Liwa is thought to be associated with the Quaternary sediments of the Ranau Formation and Mt. Pesagi. The distribution of gravity anomalies generally agree with the lineament of the SF, extending along a northwest-southeast axis. Sharp differences anomaly, high in the southwest and low in the northeast, is best seen in the central part of the survey area. The variation involves differences in the magnitude of 30 to 50 mGal. This phenomenon shows a difference in basement depth between the southwestern and northeastern parts of the area. Beyond that, control of geological evidences is thought to exert a very strong influence on the distribution of gravity anomalies in the survey area.
5.2. Bouguer Anomaly Reduction
The reduction of Bouguer anomalies to a horizontal plane is done under the assumption that uneven topography has caused its share of distortions to the data [36] . These distortions arise from the variation of vertical separation between the subsurface anomaly source and the surface measurement point where the topographical effect has not been corrected in the Bouguer and free-air corrections. Topographical effect correction is necessary to eliminate the distortions to measured gravity anomalies by bringing those anomalies into a horizontal plane. In that way, the influence of the variation in vertical distance between the measurement point and the anomaly source would be reduced.
The projection to a horizontal plane utilizes the mass-point equivalent source method, which rests on the assumption that the gravity potential field measured on the surface is a response to a continuous subsurface distribution of a certain amount of discrete mass [37] . The processing of the Liwa gravity data uses a mass-point equivalent source on a plane at the elevation of +700 m above sea level. Gravity responses are then generated on a plane at the elevation of +800 m. The choice of horizontal plane elevation is in accord with the rules set down by [37] that the depth of the plane should be 2.5Δx < h < 6Δx. Δx is the distance between a mass-point equivalent source and a plane on which gravity responses are generated. Figure 7 shows the map of Bouguer anomalies on a horizontal plane at the elevation of +800 m with contour intervals of 2 mGal.
The distribution of Bouguer anomalies, when reduced into a horizontal plane, appears different than that of the distribution plotted on the actual topography. This is especially true with the high anomaly levels in the southwest, which disappears in the horizontal rendition. This is caused by the uneven topography. The topography in this southwestern area slopes downwards to the south to an elevation of approximately +700 m. This sloping topography increases the distance to the h = +800 m plane, consequently reducing the Bouguer anomaly
Figure 7. Reduced Bouguer anomaly map of +800 m elevation plane. Contour intervals are 2 mGal. Lines AA’ and BB’ mark the cross-sections for two-dimensional modeling by the method of Talwani et al. (1959).
values. By contrast, the region of volcanic topography in the northwestern part of Liwa shows a remarkable increase in Bouguer anomaly values. This is due to the widespread distribution of volcanic rocks over the topographical area at an elevation of around +800 m.
5.3. 2-D Model of Basement Structure
Two-dimensional modelling of gravity data was employed on cross-sections along the lines of AA’ and BB’ on the map of Bouguer anomalies projected to the +800 m elevation plane (Figure 7). The cross-sections were chosen to represent a number of measured gravity points so that they would provide a subsurface image with a reliable resolution. Cross section AA’, on a SW-NE axis, is nearly perpendicular to the SF. This cross-section is intended to provide an image of subsurface structures that lie at right angles to the main fault lineament. Since our observed gravity stations are laid on the elevation of more than +600 m, we used the assumption that the Bouguer density is 2.4 g/cm3 for the two-dimensional modelling. This value is lower than the average calculated density of Liwa area 2.6 g/cm3. This assumption is used by considering that most of surficial material in the study area is composed by loose sandy tuff that commonly has lower density. Surface geological data indicate that in general Liwa comprises two major rock units, namely the Tertiary volcanic unit of Bukit Barisan and the Ranau Formation. The modelling is done by creating two simple geological model blocks with the densities of 2.67 g/cm3 for the basement rocks and 2.0 g/cm3 for the overlying sedimentary unit. The basement represents the volcanic breccia units of Bukit Barisan and the overlying sediments represent the rock units of the Ranau Formation.
Figure 8 shows simple geologic model that is produced by two-dimensional modelling of gravity data along the AA’ section. The model shows that, from the southwestern to the northeastern ends, the graben blocks of the basement exhibit strong indications of step faulting. This structural form is a characteristic of the negative flower structure formed by trans-tensional tectonic activities. The thickness of the Ranau formation is predicted to be as thick as 2000 m. The three fault blocks as shown in the AA’ models are each thought to represent the Liwa fault, the Way Robok fault, and the Sukabumi fault. Figure 9 shows geologic model for the section along BB’. This east-west section is also thought to intersect several fault and old caldera structures. The western part
Figure 8. Two-dimensional density distribution model for AA’ section. The comparison between measured and calculated gravity values, from models of (b) is shown in (a); (c) is a geological interpretation of (b).
Figure 9. Two-dimensional density distribution model for BB’ section that across the Liwa basin. The comparison between the measured and calculated gravity values from model of (b) is shown in (a); (c) is geological interpretation of (b) that shows a graben with a negative flower structure in (c).
of the model displays several primary fault steps along a NW-SE direction. It is shown that the vertical displacement of the faults in BB’ section is lower than the faults on the AA’ section model. It is probably due to the influence of the projection angle of the fault planes to the model section. On the other hand, this BB’ model clearly reveals the negative flower structure in a single sectional image. As in the previous model, the Ranau Formation rock units with a density of 2.0 g/cm3 are deposited on basement rocks with a density of 2.67 g/cm3 with a basement depth of around 2000 m.
Figure 10 is a topographic map of basement rock morphology compiled from the 2-D models in Figure 8 and Figure 9, with contour intervals of 100 m. The presence of the Sukabumi, Way Robok and Liwa faults are clearly indicated along a NW-SE line parallel with the main fault axis of the Sumatra Island. To the northeast, the elevation of the basement descends sharply to the depth of −900 to −1400 m, probably indicating the elevation of the basement of Mt. Pesagi. Circular or horseshoe-shaped structures thought to be remnants of old calderas can be clearly seen beneath Mt. Limau Kunci and Mt. Pesagi. These observations are supported by the results of Landsat imagery analysis of the Liwa region by Suwijanto [19] that revealed several circular or horseshoe-shaped morphological features as shown in Figure 2.
5.4. Local Anomalies
Bouguer anomaly is a combination of gravity potential values caused by local and regional influences. Regional anomaly is generally influenced by or is direct reflections of basement structures. On the other hand, local anomalies are essential in the qualitative interpretation of the structural features that define surface geological features. Figure 11 shows locally-generated gravity anomalies that reflect shallow subsurface geological features in the Liwa basin. These local anomaly values are obtained after the local effects were separated from the regional anomalies with a filtering method based on the 1-D Fast Fourier Transform. Coupled circular high- and low- anomaly features are found in hilly areas in the southern part of the study area. Low anomalies indicate the existence of graben while high anomalies reflect the presence of horsts, both of which are produced by trans-ten- sional tectonic activities. Observed negative local anomalies characterize zones of weak geological conditions that may characterize intensively fractured zones.
Figure 10. Topographic map of the basement rock of Liwa basin and its qualitative geological interpretation. The lineaments of fault structures (straight dashed-lines) and old caldera structures (curved dashed-lines) are well delineated. Interval contour of the basement rock elevation is 100 m. The letters G and H denote graben and horst, respectively.
Figure 11. Residual gravity map due to local effects. The graphic and numeric scales on the right indicate gravity unit in mGal.
Local anomaly lineaments extending in a northwest-southeast direction is probably a surface manifestation of the Sukabumi fault. Other lineaments found to the southwest may be surface indications of the Robok and Liwa faults. The three faults are relatively close to each other so it can be inferred that the Liwa plateau is an enormous fractured zone. A zone of locally-generated negative gravity anomaly that denotes the presence of old caldera can be clearly detected beneath Mt. Limau Kunci. However, a local negative gravity anomaly is distorted and does not clearly show the shape of a caldera structure beneath Mt. Pesagi. This is most likely caused by the lack of number of gravity data points in the area. The same possibility also applies to similar anomalies south of Liwa. Figure 12 illustrates schematically simple and most commonly used tectonic development stages in Sumatra: (a) initial tectonic stage, (b) main compression stage, (c) stress-released or tensional stage that produces normal block faulting. Those (a) to (c) stages will produce (d) a positive flower structure that compose of strike- slip and thrusting faults, and (e) a negative flower structure that compose of strike-slip and graben/normal faults. All these features are well characterized by gravity anomaly distributed in the study area.
As noted in previous sections, gravity effects that describe shallow discontinuity is indicated by the high anomaly values in the southwest towards Krui and low anomalies in the northeast on the southern slopes of Mt. Pesagi. This shallow discontinuity is a boundary plane between the basement rocks and the overlying sediments. The basement rocks consist of well-compacted Tertiary volcanic breccia with a density of 2.67 g/cm3. The se-


Figure 12. Simple and most commonly used tectonic development stages in Sumatra: (a) initial tectonic stage; (b) main compression stage; (c) stress-released or tensional stage that produces normal block faulting; Those (a) to (c) stages will produce (d) a positive flower structure that compose of strike-slip and thrusting faults; and (e) a negative flower structure that compose of strike-slip and graben/normal faults.
diments that cover these basement rocks are Quaternary volcanic products, especially sandy tuffs, and are well- known as the Ranau Formation. In contrast to the basement rocks, these sediments are poorly compacted.
The deformations that occur in the Liwa region resulted both normal and strike-slip faults along with a very extensive fractured zone. The loose Quaternary volcanic products of the Ranau Formation formed a good candidate for a groundwater reservoir in Liwa. On the other, high permeability and great thickness of nearly 2000 m of the loose sandy tuff presents problems in shallow groundwater exploitation because water tends to percolate rapidly into greater depths. Field observations show that in some places it is still possible to find wells with a groundwater level of 16 m below the surface, and even some where the water can be obtained at a depth of 10 m below the surface. This abundance of groundwater, however, can only be experienced in the wet season. In the dry seasons, the water table would fall so much lower that exploitation of water from the wells is rendered practically impossible. In such conditions the need for water must be fulfilled by utilizing the surface water sources in the area such as the rivers of Way Robok and other streams and small rivers in the Liwa area.
5.5. Three-Dimensional Model
In this study, 3-D inversion of gravity data was accomplished with the aid of two weighting factors, namely depth-weighting and minimum volume. Subsurface conditions were approximated by a set of 3-D prisms of fixed density value. Figure 13 shows the target area for the 3-D inversion of the Bouguer gravity data shown in Figure 6. The construction of 3-D prism block model is based on the distribution of interpolation points, each of which possesses the same dimensions and size.
The prisms were constructed with x-axis along an east-west direction, y-axis on a north-south direction, and z-axis is positive downward representing vertical depth. There are 25 × 19 × 10 prisms each of 2 × 2 × 0.2 km. Figure 14 shows the resulting model of 3-D inversion of Liwa gravity data for the depths of up to 2 km.
In general, the model shows that the value of rock density contrasts is relatively low at near the surface and increases steadily with depth. Rock groups with the low density contrast of 0.15 - 0.3 g/cm3, found at depths of up to 2 km from the surface, are assumed to be relatively uniform, loose or poorly compacted, and intensively
Figure 13. Target area for 3-D inversion of the Bouguer anomaly data as shown in Figure 6, where each prismatic element is marked by the distribution of interpolation points.
fractured. Other rock groups with moderate to high density contrast values of greater than 1.0 g/cm3 have been detected at the depths of over 2 km. These groups are thought to be harder, better compacted rocks that form the basement rocks of Liwa. Differences in the morphology of basement rocks can be easily recognized (see Figure 14). An anomaly of low density contrast in the north to northwestern part of the survey area is presumably characterizing a depression zone filled with poorly-compacted volcanic rocks. Meanwhile, the very high density contrasts at the elevations of 1.4 to 2.0 km shows an elongated geological structure with a northwest-southeast trend. The results of this survey support the conclusion that Liwa area is underlain by a graben showing a negative flower structure as the result of trans-tensional tectonic activities. High-density Tertiary volcanic breccia units and low-density Quaternary Ranau Formation volcanic units are present as, correspondingly, the basement rocks and the overlying sedimentary units.
6. Concluding Remarks
We have carried out subsurface imaging of rock density distributions in Liwa area by means of two-dimensional modelling and 3-D inversion of gravity data. Our study concludes that, in general, the subsurface image of rock density distribution obtained through two-dimensional modelling provides a clear picture of surface morphology of the basement rocks with structural lineaments lying parallel to the main axis of Sumatra Island. Graben and horst structures forming step faults or a negative flower structure can be clearly observed in the two-dimensional models. The fault structures with NW-SE alignment found in Liwa are thought to be closely related to the faults of Sukabumi, Way Robok and Liwa. These phenomena show that Liwa has experienced strong deformation from extensive trans-tensional tectonic activities with a very intensive fractured zone. The loose Quaternary volcanic products of the Ranau Formation formed a good candidate for a groundwater reservoir in Liwa. But high permeability and great thickness of nearly 2000 m of the loose sandy tuff present problems in shallow groundwater exploitation because water tends to percolate rapidly into greater depths. Circular or horseshoe-
Figure 14. The model of rock density distribution obtained by 3-D inversion of gravity data. The distribution of density contrasts is calculated down to the depth of 2 km. Y-and X-axes denote north and east directions, respectively.
shaped negative gravity anomalies indicating old caldera structures can be identified beneath Mt. Limau Kunci and Mt. Pesagi.
The model obtained from 3-D inversion of gravity data allows to clarify the distribution of rock density contrasts. It can be concluded that the low density contrast is found near the surface and variably increases with depth. The low density contrast of 0.15 - 0.3 g/cm3 at depth of 2 km and less below the surface is considered to characterize relatively uniform and loose or poorly-compacted rocks. Rock groups with higher density contrast greater than 1.0 g/cm3 at the depth of over 2 km are thought to be harder and better-compacted units that form the basement rocks of Liwa. The strikingly high density contrast at depth between 1.4 km and 2.0 km indicates structural lineaments extending longitudinally along a northwest-southeast axis. These lineaments are in agreement with the main structural trends of Sumatra Island. These results support the previous thought that Liwa area is comprised of a graben structure resulting from the trans-tensional tectonic processes. Higher-density Tertiary volcanic breccia and lower-density Quaternary volcanic products of the Ranau Formation each form the basement rocks and the overlying younger sediments.
Acknowledgements
With the completion of this paper, we would like to express our special gratitude to the Director of Research Centre for Geotechnology, the Indonesian Institute of Science (RCG-LIPI) for his support and facilitation of this cooperation. Special thanks are also due to the help of Cahyo Raharjo (Geophysics Program of Gajah Mada University, presently at Chevron Indonesia) in evaluating the Bouguer gravity anomaly reduction to the horizontal plane and in the 2-D modelling of gravity data used in this study. This work is a part of a joint research program conducted by Research Centre for Geotechnology, the Indonesian Institute of Science (RCG-LIPI) and Kyoto Institute of Natural History, Japan.
Cite this paper
Djedi S. Widarto,Tedi Yudistira,Jun-Ichi Nishida,Ikuo Katsura,Eddy Z. Gaffar,Susumu Nishimura, (2016) Imaging Rock Density Distribution beneath Liwa Fracture Zone in the Southern Part of the Great Sumatran Fault System, Indonesia. International Journal of Geosciences,07,598-614. doi: 10.4236/ijg.2016.74046
References
- 1. Nettleton, L.L. (1976) Gravity and Magnetic in Oil Prospecting. McGraw Hill, New York.
- 2. Piskarev, A.L. and Tchernyshev, M.Y. (1997) Magnetic and Gravity Anomaly Patterns Related to Hydrocarbon Fields in Northern West Siberia. Geophysics, 62, 831-841.
http://dx.doi.org/10.1190/1.1444192 - 3. Zeng, H., Meng, X., Yao, C., Li, X., Lou, H., Guang, Z. and Li, Z. (2002) Detection of Reservoirs from Normalized Full Gradient of Gravity Anomalies and Its Application to Shengli Oil Field, East China. Geophysics, 67, 1138-1147.
http://dx.doi.org/10.1190/1.1500375 - 4. Serpa, L.F. and Cook, K.L. (1984) Simultaneous Inversion Modeling of Gravity and Aeromagnetic Data Applied to a Geothermal Study in Utah. Geophysics, 49, 1327-1337.
http://dx.doi.org/10.1190/1.1441759 - 5. Allis, R.G. and Hunt, T.M. (1986) Analysis of Exploitation-Induced Gravity Changes at Wairakei Geothermal Field. Geophysics, 51, 1647-1660.
http://dx.doi.org/10.1190/1.1442214 - 6. O’Donnel Jr., T.M., Miller, K.C. and Witcher, J.C. (2001) A Seismic and Gravity Study of the McGregor Geothermal System, Southern New Mexico. Geophysics, 66, 1002-1014.
http://dx.doi.org/10.1190/1.1487048 - 7. Gupta, V.K. and Ramani, N. (1982) Optimum Second Vertical Derivatives in Geologic Mapping and Mineral Exploration. Geophysics, 47, 1706-1715.
http://dx.doi.org/10.1190/1.1441320 - 8. Babu, H.V.R. (2003) Relationship of Gravity, Magnetic, and Self-Potential Anomalies and Their Application to Mineral Exploration. Geophysics, 68, 181-184.
http://dx.doi.org/10.1190/1.1543205 - 9. Alatorre-Zamora, M.A. and Campos-Enriquez, J.O. (1991) La Primavera Caldera (Mexico): Structure Inferred from Gravity and Hydrogeological Considerations. Geophysics, 56, 992-1002.
http://dx.doi.org/10.1190/1.1443132 - 10. Benson, A.K. and Floyd, A.R. (2000) Application of Gravity and Magnetic Methods to Assess Geological Hazards and Natural Resource Potential in the Mosida Hills, Utah County, Utah. Geophysics, 65, 1514-1526.
http://dx.doi.org/10.1190/1.1444840 - 11. Garcia-Abdeslem, J. (2003) 2D Modeling and Inversion of Gravity Data Using Density Contrast Varying with Depth and Source—Basement Geometry Described by the Fourier Series. Geophysics, 68, 1909-1916.
http://dx.doi.org/10.1190/1.1635044 - 12. Zhang, J., Wang, C.-Y., Shi, Y., Cai, Y., Chi, W.C., Dreger, D., Cheng, W.B. and Yuan, Y.H. (2004) Three-Dimensional Crustal Structure in Central Taiwan from Gravity Inversion with a Parallel Genetic Algorithm. Geophysics, 69, 917-924.
http://dx.doi.org/10.1190/1.1778235 - 13. Blakely, R.J. (1995) Potential Theory in Gravity and Magnetic Applications. Cambridge University Press, Cambridge, 441.
http://dx.doi.org/10.1017/cbo9780511549816 - 14. Bellier, O. and Sébrier, M. (1994) Relationship between Tectonism and Volcanism along the Great Sumatran Fault Zone Deduced by SPOT Image Analyzes. Tectonophysics, 233, 215-231.
http://dx.doi.org/10.1016/0040-1951(94)90242-9 - 15. Bellier, O. and Sébrier, M. (1995) Is the Slip Rate Variation on the Great Sumatran Fault Accommodated by Fore-Arc Stretching? Geophysical Research Letters, 22, 1969-1972.
http://dx.doi.org/10.1016/0040-1951(94)90242-9 - 16. Sieh, K. and Natawidjaja, D.H. (2000) Neotectonics of the Sumatran faults, Indonesia. Journal of Geophysical Research, 105, 28295-28326.
http://dx.doi.org/10.1029/2000JB900120 - 17. Amin, T.C., Sidarto, Santosa, S. and Gunawan, W. (1994) Geology of the Kotaagung Quadrangle, Sumatera (1:250,000) GRDC-DGGMR. Department of Energy and Mineral Resources, The Republic of Indonesia.
- 18. Gafoer, S., Amin, T.C. and Pardede, R. (1994) Geology of the Baturaja Quadrangle, Sumatera (1:250,000) GRDC-DGGMR. Department of Energy and Mineral Resources, The Republic of Indonesia.
- 19. Suwijanto, Burhan, G. and Bahar, I. (1996) Remote Sensing Application for the Liwa Earthquake Evaluation and Preparation of Hazard Mitigation. Report on Remote Sensing Application for Natural Resources Management, Project TA. No. 1910-INO (ADB-BPPT), 22.
- 20. Widiwijayanti, C., Deverchere, J., Louat, R., Sébrier, M., Harjono, H., Diament, M. and Hidayat, D. (1996) Aftershock Sequence of the 1994, Mw 6.8, Liwa Earthquake (Indonesia), Seismic rupture Process in a Volcanic Arc. Geophysical Research Letters, 23, 3051-3054.
http://dx.doi.org/10.1029/96GL02048 - 21. Katili, J.A. and Hehuwat, F.H. (1967) On the Occurrence of Large Transcurrent Faults in Sumatra, Indonesia. Journal of Geosciences (Osaka City University), 10, 5-17.
- 22. Evans, R.B. and Greenwood, P.G. (1971) Applied Geophysics Unit Rep. 3, Geophysical Surveys in Selected Areas of Central and West Java, Indonesia. Institute of Geological Sciences, London. Geophysics Division 20.
- 23. Torge, W. (1980) Geodesy. Walter de Gruyter Berlin, New York, 61-62.
- 24. Hammer, S. (1939) Terrain Correction for Gravimetric Stations. Geophysics, 4, 184-194.
http://dx.doi.org/10.1190/1.1440495 - 25. International Association of Geodesy (1971) Geodetic Reference System 1967. Special Publication No. 3, Bulletin of Geodesy and Geomatics, 116.
- 26. Nishimura, S., Nishida, J., Yokoyama, T. and Hehuwat, F. (1986) Neo-Tectonics of Strait of Sunda, Indonesia. Journal of Southeast Asian Earth Sciences, 1, 81-91.
http://dx.doi.org/10.1016/0743-9547(86)90023-1 - 27. Talwani, M., Worzel, J.L. and Landisman, M. (1959) Rapid Gravity Computations for Two-Dimensional Bodies with Application to the Mendocino Submarine Fracture Zone. Journal of Geophysical Research, 64, 49-59.
http://dx.doi.org/10.1029/JZ064i001p00049 - 28. Li, Y. and Oldenburg, D.W. (1996) 3-D inversion of Magnetic Data. Geophysics, 61, 394-408.
http://dx.doi.org/10.1190/1.1443968 - 29. Boulanger, O. and Chouteau, M. (2001) Constraints in 3-D Gravity Inversion. Geophysical Prospecting, 49, 265-280.
http://dx.doi.org/10.1046/j.1365-2478.2001.00254.x - 30. Last, B.J. and Kubik, K. (1983) Compact Gravity Inversion. Geophysics, 48, 713-721.
http://dx.doi.org/10.1190/1.1441501 - 31. Guillen, A. and Menichetti, V. (1984) Gravity and Magnetic Inversion with Minimization of a Specific Functional. Geophysics, 49, 1354-1360.
http://dx.doi.org/10.1190/1.1441761 - 32. Barbosa VCF and Silva JBC (1994) Generalized Compact Gravity Inversion. Geophysics, 59, 57-68.
http://dx.doi.org/10.1190/1.1443534 - 33. Li, Y. and Oldenburg, D.W. (1998) 3-D inversion of Gravity Data. Geophysics, 63, 109-119.
http://dx.doi.org/10.1190/1.1444302 - 34. Fedi, M. and Rapolla, A. (1999) 3-D Inversion of Gravity and Magnetic Data with Depth Resolution. Geophysics, 64, 452-460.
http://dx.doi.org/10.1190/1.1444550 - 35. Menke, W. (1984) Geophysical Data Analysis: Discrete Inverse Theory. Academic Press, Orlando.
- 36. Xia, J. and Sprowl, D.R. (1991) Correction of Topographic Distortion in Gravity Data. Geophysics, 56, 537-541.
http://dx.doi.org/10.1190/1.1443070 - 37. Dampney, C.N.G. (1969) The Equivalent Source Technique. Geophysics, 34, 39-53.
http://dx.doi.org/10.1190/1.1439996
NOTES
*Corresponding author.
















