International Journal of Geosciences
Vol.05 No.12(2014), Article ID:51866,6 pages
10.4236/ijg.2014.512125
Poisson’s Ratio of Surface Soils and Shallow Sediments Determined from Seismic Compressional and Shear Wave Velocities
U. E. Essien1, A. O. Akankpo2, M. U. Igboekwe3
1Department of Science Technology, AkwaIbom State Polytechnic, Ikot Osurua, Nigeria
2Department of Physics, University of Uyo, Uyo, Nigeria
3Department of Physics, Michael Okpara University of Agriculture, Umudike, Nigeria
Email: akankpo@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 September 2014; revised 15 October 2014; accepted 12 November 2014
ABSTRACT
This paper presents the results of seismic compressional, P- and shear, S-wave measurements carried out on the unconsolidated top-soil at the different locations of the study area to determine Poisson’s ratio. In this work, seismic refraction data is used to determine Poisson’s ratio as an aid to engineering foundation. A 12-channel seismograph with signal stacking ability was used together with high frequency (100 Hz) geophones on the top-soil. The geophone intervals were set to 5 m at the all locations. In all the locations, Vp/Vs ratio ranged from 1.0289 to 1.4185 for the top layer. Vp/Vs ratio in the second layer ranged from 1.0512 to 1.5834. The Poisson’s ratio for the first layer ranged from −8.0324 to 0.2060. For the second layer, the Poisson’s ratio ranged from −0.7567 to 0.1683. The values of Vp/Vs ratio less than 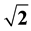 in the first layer and in some locations in the second layer resulted in negative Poisson’s ratio. The low and negative values of Poisson’s ratio are symptomatic of occurrence of ripable anisotropic materials in the locations where they occur, which suggests that indicated average depth should be removed and refilled with geomaterials that may be resilient to carry engineering loads.
in the first layer and in some locations in the second layer resulted in negative Poisson’s ratio. The low and negative values of Poisson’s ratio are symptomatic of occurrence of ripable anisotropic materials in the locations where they occur, which suggests that indicated average depth should be removed and refilled with geomaterials that may be resilient to carry engineering loads.
Keywords:
Seismic Refraction, Eket, Vp/Vs Ratio, Poisson’s Ratio

1. Introduction
The elastic properties of soils measured at low strain, such as shear modulus, Young’s modulus, or Poisson’s ratio are essential parameters for dynamic response analysis and soil-structure interaction problems and can play an important role in the study of liquefaction potential under seismic loading [1] . These parameters are also useful for the characterization of soils in terms of geotechnical and mechanical properties [2] .
Poisson’s ratio σ is a measure of the transverse strain or contraction to longitudinal strain or extension resulting from a change in normal stress under compression or dilatation [3] . A change in the wave propagation from one lithology to another or from an unsaturated to a saturated medium leads to variation in the value of σ from 0 (indicating a considerable change in volume) to 0.5 (indicating no volumetric change, corresponding to fluids). Also, σ can have negative values, and these indicate certain properties. Poisson’s ratio σ has been effectively used in engineering, groundwater and hydrocarbon investigation. Poisson’s ratio or compressional wave velocity are good indicators of the depth of saturation in deposits.
In a previous work, a σ range of 0.4982 - 0.4997 was obtained for clays [4] ; σ range of up to 0.49 was obtained for shallow, clayey, saturated sediments [5] . Also, a σ value of 0.1 was obtained for gas saturated sediments [6] [7] . The softer and smaller the grains (e.g. clay and silts), the higher the σ value, and vice versa (e.g. sands and gravels). The overburden and pore-pressure gradients are main factors controlling the fracture dimensions that can be predicted from knowledge of σ and other parameters [8] . A σ range of 0.27 - 0.40 was obtained for shaly sandstone reservoirs saturated with multi phase fluids [9] ; a σ range of 0.14 - 0.41 was represented for formations of different lithologies and saturants [10] .
The discrepancy in lithology from one layer to another (due to variations in porosity, size, shape, type and stiffness of the grains), the clay content, the air and water saturations, the anisotropy and the high degree of heterogeneity, both laterally and vertically, cause wide variation in σ (from −0.15 to 0.47). Also, σ increases with depth, with increasing water saturation and with decreasing porosity [3] . In this paper, seismic refraction data is used to determine Poisson’s ratio as an aid to engineering foundation.
2. Location and Geology of the Study Area
The study area, Eket lies between latitudes 4˚37' and 4˚7'N and longitudes 7˚38' and 8˚00'E. It has an estimated area of 214 km2 (Figure 1). The study area belongs to the low-lying coastal deltaic plains of southern Nigeria [11] . The terrain is virtually flat to gently undulating, sloping generally towards the Atlantic Ocean. Elevation varies from about 100 to 120 m at the northern part of the study area to near sea level at the southern part [12] . The surface drainage basin within the study area is mainly due to the Qua Iboe River which drains the western part [6] .
Geologically, the study area falls within the Niger Delta area. The geologic formation in the Niger Delta area is made up of the Akata Formation (shales, intercalated sands and sandstones), the Agbada Formation (sands and sandstones intercalated with shales) in the middle and the Benin Formation (Coarse grained, gravelly sands with minor intercalations with clay) at the top [13] . However, only the Benin Formation otherwise called the coastal plain sands is exposed in the study area where the investigation concentrates. The coastal plain sand covers 80 percent of the area and forms the major aquiferous and foundation zones of the study area. The area is generally porous and permeable and this is usually interrupted by clay-sand sequence at different depths [14] [15] .
3. Methodology
The seismic study was based on recording the travel time of an elastic wave travelled through the ground, refracted from a subsurface, and received via geophones on the surface. Seismic P- and S-waves were recorded using vertical and horizontal components geophones (100 Hz), laid along a line with 5 m spacing, and connected to a 12-channel digital recorder. The required energy for P-wave measurement was created by a sledge hammer hitting the wooden cone at the shot points. The S-wave was created by hitting the ends of a flat-lying wooden timber loaded by a person, the weight of which increases the friction and the contact area of the timber with the ground surface [16] .
The data obtained from the seismograph (seismogram) were processed using Pickwin software to obtain the arrival time for P-wave and S-wave. With the geophone separations of 5 m interval, T-X graph were plotted for the different locations using IX Refrax software and the inverse of the slope were obtained as velocity for each of the layer penetrated [17] . The Pick-win software helped in picking the arrival times while the IX Refrax directly converted the slope into Velocity for the different layers. The IX Refrax also gave the depth of each of the layers penetrated.
Figure 1. Location map of study area.
The velocity variations obtained gave the geological implications of the geomaterials. The 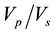 ratio usually viewed as lithology discriminator was determined for each location. Poisson’s ratio (σ) were calculated for different locations using this expression [17]
ratio usually viewed as lithology discriminator was determined for each location. Poisson’s ratio (σ) were calculated for different locations using this expression [17]
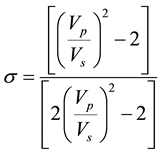 (1)
(1)
4. Result and Discussion
To actually map the elastic constants which depends on lithology, the 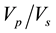 ratio usually viewed as lithology discriminator were determined for each location (Table 1). For compressional and shear waves, the velocity increases with depth. The underlain velocities were all greater than the overlain velocities at all the locations (Idua, Afaha Eket, Ikot Ebiyon, Ikot Use Ekong, Ikot Udofa and Etebi).The ratio, which is a lithology discriminator, was determined for each of the locations and the values seem to reflect the porous and air-filled environment. Table 1 indicates a significant depth of layers with anisotropic materials. It also shows that the ratio of average Vp and Vs is about 1.5 in the second layers at Idua, Afaha Eket and Ikot Udofia.
ratio usually viewed as lithology discriminator were determined for each location (Table 1). For compressional and shear waves, the velocity increases with depth. The underlain velocities were all greater than the overlain velocities at all the locations (Idua, Afaha Eket, Ikot Ebiyon, Ikot Use Ekong, Ikot Udofa and Etebi).The ratio, which is a lithology discriminator, was determined for each of the locations and the values seem to reflect the porous and air-filled environment. Table 1 indicates a significant depth of layers with anisotropic materials. It also shows that the ratio of average Vp and Vs is about 1.5 in the second layers at Idua, Afaha Eket and Ikot Udofia.
This result indicates that even up to the second layer the ground has an air-filled porous structure. The almost 1.5 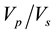 ratio observed in the above locations point to the fact that the ratio of incompressibility is almost unity. The
ratio observed in the above locations point to the fact that the ratio of incompressibility is almost unity. The 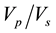 ratio in the first layer is low in parts of the North and South. However, higher values are seen at the North West of the study area (Figure 2). In the second layer, higher values of the
ratio in the first layer is low in parts of the North and South. However, higher values are seen at the North West of the study area (Figure 2). In the second layer, higher values of the 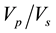 ratio are obtained in the Northeast and in the South-eastern region of the study area (Figure 3).
ratio are obtained in the Northeast and in the South-eastern region of the study area (Figure 3).
The seismic velocity ratio (compressional and shear wave velocity ratio,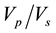 ) is especially sensitive to the
) is especially sensitive to the
Table 1. Summary of layer parameters and poisson’s ratio in the area.
Figure 2. 2-D contour map of layer one Vp/Vs ratio in the study.
fluid in the pores existing in the sedimentary rocks. Particularly, the 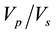 ratio in the gas saturated environments is much lower than liquid saturated environments [6] . A study on the porous environment for the
ratio in the gas saturated environments is much lower than liquid saturated environments [6] . A study on the porous environment for the 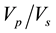 ratios was carried out and the result revealed
ratios was carried out and the result revealed 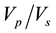 ratios of 1.9, 1.8 and 1.6 to 1.75 for limestone, dolomite and sandstones respectively [18] .
ratios of 1.9, 1.8 and 1.6 to 1.75 for limestone, dolomite and sandstones respectively [18] .
Poisson’s ratios were calculated for the different locations and the values are shown in Table 1. Table 1 shows negative Poisson’s ratios which resulted for 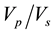 ratios less than
ratios less than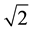 . The negative values of Poisson’s ratio are symptomatic of occurrence of ripable anisotropic materials in the locations where they occur [19] . Table 2 shows typical values of Poisson’s ratio [20] [21] .
. The negative values of Poisson’s ratio are symptomatic of occurrence of ripable anisotropic materials in the locations where they occur [19] . Table 2 shows typical values of Poisson’s ratio [20] [21] .
Table 2. Typical values of Poison’s ratio after Sharma et al. (1990) and Davidovici (1985).
Figure 3. 2-D contour map of layer two Vp/Vs ratio in the study area.
Poisson’s ratio for layer one has higher values at the Northern part while lower values are seen at the Southern region. The higher negative values of Poisson’s ratio in the South shows higher degree of anisotropy in this zone and this could be attributed to the complex muddy materials and flooding events in this region (Figure 4). For layer two the Poisson’s ratio distribution shows that the Eastern region has higher values than the Western zone (Figure 5). At the North Western zone, a higher degree of anisotropy is attributed to the negative Poisson’s ratio in the second layer. The value of σ increases with depth, which may be attributed to the fact that the soils and sediments are younger and more compressible near the surface, but become less compressible and more plastic with depth [3] .
5. Conclusion
Seismic velocity ratio (compressional and shear wave velocity ratio,



Figure 4. 2-D contour map of layer one Poisson’s ratio in the study area.
Figure 5. 2-D contour map of layer two Poisson’s ratio in the study area.
The values of 

References
- Youd, T.L., Idriss, I.M., Andrus, R.D., Arango, I., Castro, G., Christian, J.T., Dobry, R., Finn, W.D.L., Harder, L.F., Hynes, M.E., Ishihara, K., Koester, J.P., Liao, S.S.C., Marcuson, W.F., Martin, G.R., Mitchell, J.K., Moriwaki, Y., Power, M.S., Robertson, P.K., Seed, R.B. and Stokoe, K.H. (2001) Liquefaction Resistance of Soils: Summary Report from the 1996 NCEER and 1998 NCEER/NSF Workshops on Evaluation of Liquefaction Resistance of Soils. Journal of Geotechnical and Geoenvironmental Engineering, 127, 297-313. http://dx.doi.org/10.1061/(ASCE)1090-0241(2001)127:4(297)
- Karrayand, M. and Lefebvre, G. (2008) Significsnce and Evaluation of Poisson’s Ratio in Rayleigh Wave Testing. Canadian Geotechnical Journal, 45, 624-635. http://dx.doi.org/10.1139/T08-016
- Salem, H.S. (2000) Poisson’s Ratio and the Porosity of Surface Soils and Shallow Sediments, Determined from Seismic Compressional and Shear Wave Velocities. Geotechnique, 4, 461-463. http://dx.doi.org/10.1680/geot.2000.50.4.461
- Davis, A.M. and Schultheiss, P.J. (1980) Seismic Signal Processing in Engineering-Site Investigation: A Case History. Ground Engineering, 13, 44-48.
- Meissner, R., Stuempel, H. and Theilen, F. (1985) Shear Wave Studies in Shallow Sediments. In: Helbig, K. and Treiter, S., Eds. Seismic Shear Waves, Handbook of Geophysical Exploration, Geophysical Press, London, 225-253.
- Tatham, R.H. (1982) Vp/Vs and Lithology. Geophysics, 47, 336-344. http://dx.doi.org/10.1190/1.1441339
- Tatham, R.H. (1985) Shear Waves and Lithology. In: Helbig, K. and Treiter, S., Eds., Seismic Shear Waves, Handbook of Geophysical Exploration, Geophysical Press, London, 87-133.
- Labudovic, V. (1984) The Effect of Poisson’s Ratio on Fracture Height. Journal of Petroleum Technology, 36, 287-290. http://dx.doi.org/10.2118/10307-PA
- Salem, H.S. (1993) A Preliminary Study of the Physical Properties of the Terra Nova and Hibernia Oil Fields in the Jeanne d’Arc Basin, Offshore Newfoundland, Canada. Geological Survey of Canada, Halifax, NS, OFR 2686, Dossier Public.
- Tiab, D. and Donaldson, E.C. (1996) Petrophysics. Theory and Practice of Measuring Reservoir Rock and Fluid Trans- port Properties. Gulf Publishing, Houston.
- Emujakporne, G.O. and Ekine, A.S. (2009) Determination of Rock Elastic Constants from Compressional and Shear Wave Velocities for Western Niger Delta, Nigeria. Journal of Applied Science and Environmental Management, 13, 53-55.
- George, N.J., Akpan, A.E., George, A.M. and Obot, I.B. (2010) Scholars Research Library: Determination of Elastic Properties of the Overburden Materials in Part of Akamkpa, Southern Nigeria Using Seismic Refraction Studies. Archives of Physics Research, 1, 58-71.
- Okwueze, E.E. (1988) Mapping Bedrock Surface and Lithology with Seismic Refraction. Journal of Mining Geology, 27, 16-27.
- Okwueze, E.E. (1991) Shear Wave Observation in Seismic Refraction Prospecting. Journal of Mapping and Geology, 24, 61-65.
- Ekwueme, B.N., Nyong, E.E. and Peters, S.W. (1995) Geological Guide to Obtain Massif, Calabar Flank and Mamfe Embayment, Southeastern Nigeria.
- Essien, U.E. and Akankpo, A.O. (2013) Compressional and Shear-Wave Velocity Measurements in Unconsolidated Top-Soil in Eket, South-Eastern Nigeria. The Pacific Journal of Science and Technology, 14, 476-491.
- Atat, J.G., Akpabio, G.I., George, N.J. and Umoren, E.B. (2012) Geophysical Assessment of Elastic Constant of Top Soil Using Seismic Refraction Compressional and Shear Wave Velocities in the Eastern Niger Delta. International Journal of Modern Applied Physics, 1, 7-19.
- Pickett, G.R. (1963) Acoustic Character Logs and Their Application in Formation Evaluation. Journal of Petroleum Technology, 15, 659-667. http://dx.doi.org/10.2118/452-PA
- Love, A.E.H. (1927) A Treatise on the Mathematical Theory of Elasticity. Cambridge University Press, Cambridge, 104.
- Sharma, H.D., Dukes, M.T. and Olsen, D.M. (1990) Field Measurement of Dynamic Moduli and Poisson’s Ratios of Refuse and Underlying Soils at a Landfill Site. In: Landva, A. and Knowles, G.D., Eds., Geotechnics of Waste Landfills: Theory and Practice, American Society for Testing and Materials, Philadelphia, 57-70.
- Davidovici, V. (1985) G nie parasismique. École Nationale des Ponts et Chauss es, Paris, 1105.







