International Journal of Geosciences
Vol.05 No.10(2014), Article ID:50241,11 pages
10.4236/ijg.2014.510101
Thermo-Electrochemical Processes of the Earth’s Degassing Creating Geomagnetic Field and Changing Its Value and Direction (Thermodynamic Approach)
Alexander Vol
OSHADI Drug Administration Ltd., Rehovot, Israel
Email: alex@oshadi-da.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 July 2014; revised 9 August 2014; accepted 5 September 2014
ABSTRACT
The currently accepted theory of self-exciting dynamo generating magnetic field of the Earth and its shortage of energy is critically reviewed. Based on thermodynamic approach, a new hypothesis of the Earth’s magnetic field, created by thermo-electrochemical processes of the Earth’s degassing, gravitational differentiation and their energy, is proposed. The ion-exchange, extraction and solidification are sources of the ionic currents on solid core and lower mantle boundaries. These currents are carried by thermo-chemical flows, which create the primary exciting magnetic field. This field is amplified mostly by thermoelectricity generated by heat flow thus improving the heat and matter transport from the Earth’s core and lower mantle to surface. Migration of the solidification zones and inner core precession are the main causes of changes of the main magnetic field intensity and reversals of its polarity.
Keywords:
Degassing, Gravitational Differentiation, Electrochemistry, Thermoelectricity, Geomagnetism

1. Problems with Geodynamo Paradigm
According to the existing paradigm, the Earth’s magnetic field is generated in the fluid outer core by a self-ex- citing dynamo process, wherein electrical currents flowing in the slowly moving molten iron generate the magnetic field [1] -[3] . Supplementary numerical models were reviewed and analyzed by Thompson [4] , Stern [5] and Glatzmaier [6] . In addition to energy-sources in the Earth’s core, the magnetic field observable at the Earth’s surface has some sources in its crust and in the ionosphere and magnetosphere. Satellite measurements of these currents were used by Geeta Vichare and R. Rajaram for comparison of different models of Geomagnetic Field (GMF) [7] .
Herndon [8] noted that probability of the natural heat convection is very small in the outer core because of the high viscosity and the little difference of density, which is less than 3%, and that such a convection as a power source of the geodynamo formation and maintenance would be insufficient.
The relatively full analysis of a self-excited induction generator was proposed by Ofualagba and Ubeku [9] . The residual magnetization as a main source of the rotor currents generation was proposed by Sohre and Nippes [10] . Sohre patented riding brushes to control these currents [11] . Our studies of spontaneous self-exciting rotor currents in turbine [12] [13] as well as the results of Kirschner and Moon [14] allowed suggesting the following necessary conditions for its work: the initial or residual critical level of magnetization, fast speed of relative motion and high conductivity of the rotor-stator spontaneous “exciting” circuit [9] [12] [13] , existence of the permanent magnets on rotor (stator) of a generator, or formation of a special exciting circuit [14] . The references cited above demonstrate the principal impossibility of the self-excited geodynamo existence because the Earth’s interior does not correspond to the known conditions of a self-exciting generator.
The observed reversibility of the main magnetic field is also an unsolved problem. Any dynamo converts mechanical energy into electrical; thus its operation is accompanied by significant mechanical losses and change of the field polarity demands corresponding changes of the matter flows and compensation of the inertia.
Generation of the main geomagnetic field by outer core currents or by thermo-chemical convection needs a very high intensity of convection and that of the density of currents. Such a process would not accelerate transport of energy and matter from core to surface, and this is inconsistent with the thermodynamic laws.
The improved physico-mathematical models were proposed for explanation of the Earth’s magnetism variability and reversibility [15] [16] , however these models cannot propose an unambiguous solution of GMF problems. The self-exciting dynamo theory has to include the mathematical model of the natural heat convection, which provides self-organization of the flows. According to Glatzmaier [6] , “The system of equations represents conservation of mass, momentum, energy, and magnetic flux, an equation of state, and the magnetic induction equation. A computer solves this system of equations, one numerical time step at a time for typically millions of time steps, to provide the time evolution of the three components of the fluid velocity, the three components of the magnetic field, and the thermodynamic perturbations in a three-dimensional (3D), rotating, spherical shell of electrically conducting fluid. The numerical solutions are self-consistent in the sense that all of these variables are part of the 3D time-dependent solution and that convection and magnetic field generation are driven only by the heat flux through the boundaries.”
All the known models of geodynamo, the Earth’s core and mantle convection are based on the observed phenomena: the Earth’s magnetic field and continental plates’ motility. In a common case, such a system of equations cannot be solved. Any geo-dynamo model is heuristic, based on separate formal calculations of separate aspects of interaction of the cyclonic convective motions with toroidal field [4] .
It is easy to agree with Herndon’s conclusion [17] : “As is the case for the Earth’s mantle, justification for the Earth-core convection cannot be obtained by calculating the Rayleigh number because the Earth’s core is neither incompressible nor of uniform density. Although the Earth’s core is liquid, it is ‘bottom heavy’, i.e. its density at the bottom is about 23% greater than at its top. The potential decrease in density by thermal expansion, less 1%, cannot make the core ‘top heavy’ as described by Chandrasekhar; thus convection is not to be expected.” Herndon [17] also rejected heat convection as a motive force of geodynamo and energy transport from the core to the Earth surface.
In its place he proposed a planetary nuclear reactor as the main source of energy of the magnetic field [8] ; he proposed also “mantle decompression thermal tsunami” in combination with plumes, which he named “heat channeling”, as a basic mechanism of the matter and energy transport [17] .
The conclusion about the impossibility of free heat convection in the Earth’s core and mantle emerges from the known laws of heat and mass transfer, which are used for calculation of circulation in chemical apparatuses [18] , steam boilers [19] and nuclear reactors [20] .
As it may be expected, the surface friction and hydraulic impedance are very serious problems for reliable cooling of any apparatus or reactor. Significant difference of water and steam-water mixture densities and careful flow organization are necessary conditions for maintenance of free heat convection [18] [19] .
In addition, it is difficult to agree with the natural nuclear fission reactor hypothesis. The Gabon rich uranium deposits formed about two billion years ago in a marine sandstone layer in the Franceville Basin. The hydrothermal water was carrying uranium into sandstone thus forming and cooling core. This water acted as an effective neutron moderator. The abundance of the fissile isotope 235U was 3.1% of the natural uranium 1.7 billion years ago, which is close to the enrichment used in some of today’s reactors. Because 235U has a shorter half-life than 238U, it decays more rapidly, and the current abundance of 235U in natural uranium is about 0.7%. Water stream prevented long-time poisoning of this reactor by fission product. There can be observed a fingerprint of fission process that allows estimating reactor power about 100 kW pulse operation of 30-minute-long with an interval about 2.5 hours for reactivity restoration [21] [22] . It is difficult to perceive existence of anything similar in the Earth’s core.
The conclusion must be that formation and stable operation of any type of geodynamo are impossible under terrestrial conditions because of the laws of electrical engineering.
The free heat convection and geodynamo cannot improve energy and matter transport from the Earth’s core to its surface also because of common thermodynamic laws (Figure 1).
The natural heat convection—free convection—is a heat machine. The maximal efficacy of such a machine is limited by Carnot cycle and depends on the difference of temperatures between heater and cooler. The motive force of such convection is a difference of matter density. The well-known sample of such convection is natural circulation in a boiler, a chemical and a power reactor, etc. Any generator is a machine for conversion of mechanical energy into electrical. Such a conversion is accompanied by dissipative losses which must be compensated by energy source.
As it is shown in Figure 1 the total dissipative losses include: an internal and boundary friction of the moving flows, an electromechanical interaction between flows and magnetic field, Joule heating of the conductive matter flow (Ohm law), and inductive generation of the eddy current into the surrounding matter and additional losses for it.
It is evident that the geodynamo paradigm proposes the way of heat energy conversion that increases heat production and internal energy level; thus it would decrease heat transport and entropy production rate which contradicts to the laws of thermodynamics.
In 2005-2012 we put forward a conceptional system of hypotheses to explain the conservation of energy during the Earth’s accretion, its quasi-stable release by primordial H- and He-degassing and of the crucial role of the energy of degassing-comprising-reactions in endogenic processes [23] [24] . Specific mechanisms and chemical processes were proposed for the gas-liquid mantle plumes melting through the solid mantle using heat- energy released in reactions of their metamorphic and chemical transformation under gradual decrease of pressure and temperature; volcanic gases were put forward as energy carriers. The 3He performance as a unique measuring transformer correlative to the internal heat flow was used for calculation of energy release by degassing; it equals to 5.12 × 1020 J/year, an amount of energy five-fold greater than the entire energy loss involved in earthquake and volcanic activity.
2. The Proposed Hypothesis: Thermoelectric-Electrochemical Model of the GMF
This proposed herein hypothesis presents the magnetic field explanation as a “side effect” of the Earth evolution, which includes:
1) The physicochemical processes of solidification of the inner core and extraction of substances from the lower mantle causing ionic currents;
Figure 1. Diagram of the energy conversion in geodynamo model.
2) Gravitational differentiation creates thermo-chemical flows, which also carry ionic currents;
3) The fast rotation deflects thermo-chemical flows by Coriolis forces thus creating exciting magnetic field;
4) Amplifying of the exciting magnetic field by electrical currents generated by thermoelectric processes accompanying the significant heat flow from core to surface and space, which comprise primordial H- and He- degassing of the Earth [23] [24] .
2.1. Chemical Reactions Generate Ionic Currents on the Boundaries of the Liquid Core
Solidification and growth of the solid core take place at the temperatures that are very close to melting points of the matter under the pressure given there. However, the homogeneous solidification is possible only in conditions of significant over-cooling, that may be observed on the magma solidification fronts according to Bruce D. Marsh [25] . Such a condition is difficult to imagine on the solid-liquid cores boundary. “Seismic data on the structure of the inner core reveal a bewildering degree of complexity. Most surprising is the observation that seismic properties differ between the eastern and the western half of the inner core” noted Bruce A. Buffet [26] . Deuss A. et al. [27] described experimental observations, which showed a strong anisotropy on the western and relatively little anisotropy on the eastern hemisphere of the inner core. Monnereau et al. [28] concluded that the inner core growth proceeded with lateral material motion within it. According to their analysis, the transport of the inner core’s matter is sufficiently fast, melting and solidification should occur in the opposite hemispheres. Mattesini et al. [29] wrote that the Earth’s inner core has an axisymmetric anisotropic structure with seismic waves traveling ≈3% faster along polar paths than along equatorial directions.
Solidification of the inner core along the boundary with outer core occurs under shear-compression at the liquid-solid interface, a process that favors the development of oriented iron crystal. There is at least a permissive evidence for seismic discontinuity within the inner core, which allows separating zones of the oriented iron crystal, mushy zones with high attenuation and zones of possible discontinuity, which may be a phase change ( [1] , page 182-185).
Duess et al. [27] , and Mattesini et al. [29] wrote that observed hemispherical differences in seismic properties may be explained by differences in average crystal sizes. The solidification and melting would be accompanied by redistribution of compounds between solid and liquid phase according to Zhang and Yin [30] , Ricoplleau et al. [31] , Tsuno et al. [32] . It was proposed by Shun-ichiro Karato that “Maxwell stresses squeeze in the inner core toward the rotational axis, moving material from region of high stress (the outer part of the inner core) to the region of low stress (near the rotational axis). Material that reaches the low stress region will melt and flow outward replacing the material lost from the high-stress region” [33] . The Robertson-Glickman model of liquid metal embrittlement describes the other mechanism of the fast transport redistribution and localization of the “dissolving” and deposition zones [34] [35] . The main accelerating factors are considered to be 1) fast diffusion of metals in liquid phase that enables the fast mass transfer out of the crack tip and 2) wetting-induced surface reconstruction. There is also a spontaneous process of the Mullins grooving dramatically accelerated by blunting the tip due to the local plastic strain [36] . The motive force of the transport includes electromigration [37] . Electrochemical processes including solute transport and deposition of the materials through melt or electrolytes are well known and used in industry. Rate and efficacy of these processes are much more than Maxwell stress squeezing.
It seems reasonable to expect that physicochemical processes on the boundaries of the liquid core with the solid core and the lower mantle generate ionic currents. Juzeliúnas and Hinken [38] observed magnetic field generated by such current on the liquid-solid boundary during solidification of pure metal. There are good reasons to expect that the current’s density at solidification from mix of salts (silicates, alum silicates, oxides, etc.) and selective solutes from mantle will be much higher than at pure metal phase boundary.
2.2. Thermo-Chemical Flows as a Natural Carrier of Ionic Currents
Keondjan [39] wrote that gravitational differentiation provides extraction of the high density compounds from mantle into outer liquid core, their transport and decomposition on the surface of inner core and simultaneous extraction and transport from inner core to the Earth’s surface of low density compounds and gases. Research done by Kohlstedt and Holtzman [40] resulted in conclusion that tidal waves cause periodical deformations which accelerate matter transport and extraction from the mantle and solid core. These processes are accompanied by phase transitions and according to Parmentier [41] may cause superplastic deformation of the mantle.
The above listed processes lead to the creation of thermo-chemical flows or thermo-chemical convection first of all in the liquid core, and, secondly, in mantle plumes. These were studied and described on the basis of laboratory experiments, observations and theoretical analyses by Aubert et al. [42] , Gonnermann [43] , Gonnermann et al. [44] , Jellinek et al. [45] . Aubert et al. [42] also note that existence of thermo-chemical flows must be inevitable and that coupling of heterogeneity of the core with heterogeneity of the low mantle is also inevitable.
Furthermore, results of Gonnermann et al. [44] proposed a scaling law that quantifies the fraction of core heat flow associated with plate-scale mantle flow, as well as the lateral heterogeneity in core-mantle boundary (CMB) heat flux. Gonnermann and Mukhopadhyay suggested recycling and mixing of noble gases in the convecting mantle, thereby decreasing the rate of mantle degassing and leaving significant amounts of noble gases in the processed mantle [46] .
Along with the cited above considerations, it should be noted that degassing process and interaction of the thermo-chemical flows with inner and outer core medium will be influenced by the shear strains caused by differential rotation of the core; strains accelerate redistribution of chemical substances and compounds. Difference of the rotation rate is 1 ± 0.2 deg/y ( [1] , p. 185). There are inclinations of the Earth rotation axis and the Moon orbit in relation to the ecliptic plan causing the complete structuring of tidal waves. The tidal waves cause high-rate strains in the core and mantle, which also accelerate the different physicochemical reactions.
Phase transitions [41] and matter-saturation by hydrogen and helium cause dramatic decrease of the mantle and rock viscosity [47] [48] , thus promoting localization of deformations and auto-focusing of the matter-heat flows.
Primordial hydrogen-helium degassing processes include consequences of the mutually induced chemical reactions accompanied by energy release [23] [24] . These, in their turn, also decrease local viscosity and prevent fast cooling of the ascending flow by the relatively low-temperature ambient matter.
2.3. Coriolis Forces Cause Deflection of the Thermo-Chemical Flows with Ionic Currents Thus Creating Exciter in Outer Core
The gravitational differentiation and degassing create thermo-chemical flows in the outer liquid Earth’s core. The Earth’s rotation causes horizontal deflection of the vertical (radial) flows, vertical deflection of the horizontal motion and horizontal deflection of the horizontal motion. The history of their discoveries was described by Persson [49] . There is a combination of the gravitational, rotational and frictional formation of the flows of helical or spiral structure, which have an opposite direction in the northern and southern hemisphere: those are known as Ekman’s spirals and flows [49] . The same rules were applied to the Earth’s liquid core by Aubert et al. [50] , who proposed an explanation of the secular variation of the geomagnetic field by two mechanisms relying on the inner core: first is the gravitational coupling, which alings the inner core with the mantle, forcing the flow of liquid in the outer core into a giant, westward drifting; second is the differential inner core growth. Thus, Sreenivasan and Jellinek [51] proposed an explanation of the Martian magnetic field as created by the helical structure of Tharsis plume deflected by Coriolis forces.
The differential inner core growth causes an asymmetric buoyancy release in the outer core as it was shown by Prior [52] . Centrifugal and Coriolis forces assist in the formation of thermo-chemical flows, which bear the ionic currents creating the corresponding magnetic field. These currents generated in the northern and southern hemispheres create opposite directions of the magnetic field. There are inevitable currents between solidification and dissolving (melting) zones of mantle and solid core, which cause descending flows in the polar zones due to decreased centrifugal forces there. A full range of these flows creates a dipole and non-dipole (quadrupole, etc.) components of the exciting magnetic field in the outer core.
It must be emphasized that ionic currents are generated by electrochemical processes on the solid core and lower mantle according to the proposed herein hypothesis.
There is a temporal variation of this field due to precession of the solid core and migration of the solidification zone.
This may be more understandable from the sketches on the Figure 2 and Figure 3.
The primary source of the ionic current is the electrochemical process of solidification of the inner core and extraction of the fusible components from the mantle. The Earth’s core magnetic field (GMF’s exciter) is a result of the physicochemical processes on the solid core—the liquid core and the boundaries between liquid core low mantle generating ionic currents, of thermo-chemical flows bearing these currents and of the Earth rotation causing deflection of these flows.
Figure 2. Local solidification process causes asymmetry of the thermo-chemical flows and ionic currents in equatorial plane.
Figure 3. Ionic current and thermo-chemical flows create exciting magnetic field, which is amplified by thermoelectric and chemical processes in the mantle. H- and He-degassing release the latent energy of power plumes, earthquakes and volcano activity.
2.4. Thermoelectricity Creating the Main Magnetic Field
The geodynamo theory assumes that the main magnetic field of the Earth is generated by liquid core current (97% - 99%), crustal field (1% - 2%), and external field (1% - 2%) [7] . Thus it means that dipole ingredient at the core-mantle boundary is a factor about 8 times stronger than at the surface. It also means that all field harmonics of order n are a factor 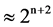 stronger than at the surface [53] . Generation of such currents in the liquid core demands a very intensive convection, which is impossible [8] . According to the geodynamo theory, the mantle cannot create magnetic field due to high viscosity and the impossibility of fast convection [54] . However, it does not take into account the very significant flow of heat from the core to the surface generating thermoelectricity due mainly to the degassing process.
stronger than at the surface [53] . Generation of such currents in the liquid core demands a very intensive convection, which is impossible [8] . According to the geodynamo theory, the mantle cannot create magnetic field due to high viscosity and the impossibility of fast convection [54] . However, it does not take into account the very significant flow of heat from the core to the surface generating thermoelectricity due mainly to the degassing process.
This proposed herein hypothesis suggests the mantle thermoelectricity as the main generator of geomagnetic field (GMF), which amplifies the magnetic field of the core. The core exciter may create a relatively small magnetic field, which would control the formation of the main GMF. The main field may be several orders stronger than the field generated by the solid-liquid core-mantle galvanic and convective currents. The amplification of the core field and acceleration of the matter and heat transport by thermoelectric phenomena decreases free energy of the system and increases the rate of entropy production thus corresponding to the basic thermodynamic principles.
The heat and matter flows from the Earth’s core to its surface create thermoelectricity mainly at the phase boundaries. Self-focusing of the matter and heat transport leads to formation of mantle-plumes and hot-spots distributed as described by Jellinek et al. [45] . Plumes activity is accompanied by the local thermo-galvanic phenomena and correspondingly by local magnetic anomalies. The thermodynamics of the thermoelectric phenomena was described by Goupil et al. [55] ; the certain thermoelectric phenomena at the solid-liquid interface of silicon were studied by Rötzer et al. [56] . Many thermoelectric devices and systems use these phenomena for control of temperature and heat flow [57] [58] . The thermoelectric transducers converse into electricity of more than 0.1% of the heat flow at a relatively small heat flow density [55] [58] .
Following is the estimation of thermoelectricity we need for GMF generation:
The total Earth’s magnetic field energy and its losses were estimated by Humphreys [59] :
· the total magnetic field energy is about 7 × 1018 J;
· the observed dipole and non-dipole energy losses are about 364 × 1015 J per 30 years.
This value corresponds to average intensity of losses about 1.4 × 1011 W. The total heat flow through the Earth surface is about 46.7 × 1012 W ( [60] , Table 7). Thus, generation of thermoelectricity that provides GMF, accounts for less than 0.3% of the Earth’s heat flow. Formation of thermoelectricity is a spontaneous phenomenon, which accelerates energy and matter transport.
The simplest diagram of the proposed main GMF formation is shown below. The GMF’s oscillations of intensity and direction, as well as of the local magnetic anomalies, are the natural results of the matter and heat transport from solid core to surface (Figure 4).
Hydrogen and helium degassing through the mantle includes their interaction with the surrounding. Implantation of hydrogen and helium in the matter increases concentration of defects: pores, vacancies, Frenkel-pairs, dislocations, etc. [61] - [63] . These defects enhance gas and heat transport. Moreover, gas flows increase the rate of electrochemical processes on the phase boundaries and may take part in thermo-electrochemical processes (hydrogen electrode is a good example), thus generating additional electrical currents and corresponding magnetic fields.
The Earth’s degassing [23] [24] causes also formation and collapse of gas bubbles, which generate shock waves and dramatically accelerates chemical reactions. Certain parameters of the reactions on the shock waves front were described by Liberman et al. [64] , the most used and known example of this phenomenon being detonation of explosives.
Figure 4. The energy conversion according to the proposed model.
The following conditions are necessary for GMF generation: existence of the source of ionic (electric) currents, relatively fast rotation of the planet and energy flow generating thermoelectricity; presumably these generate magnetic fields also on some other planets and larger moons (Table 1).
The data listed in Table 1 validate the proposed hypothesis. The Jupiter, Saturn, Uranus and Neptune have strong magnetic fields. The Mercury and Venus have mass and heat flow similar to the Earth’s, however the magnetic field of the Mercury is smaller than that of the Earth by factor 103 and the Venus has no detectable magnetic field. This may be explained by their smaller than the Earth’s rotation rate by a factor ≈59 and 243 correspondingly.
The Jupiter moons generate their own magnetic field depending on their mass, rotation rate and heat flow density. The solidification and dissolution processes generate ionic currents and thermo-chemical flows. Fast rotation causes deflection of these flows. The tidal waves cause the internal friction, which releases significant part of energy flow liberated from the moon surface.
3. Variability and Reversibility of the GMF
One of the weak points in the geodynamo paradigm is its liability in explaining the changing in intensity of GMF and reversals of its polarity. Geodynamo converts mechanical energy to electricity thus any reversibility of field needs reversibility of motion with corresponding overcoming the inertial forces, which is out of the question.
The proposed herein hypothesis explains these processes as follows: for changing intensity and polarity of GMF it is enough to change the parameters of its exciter. The typical power of exciter is from 3% to 0.5% from
Table 1. Properties of solar planets, their moons and magnetic fields.
Notes: ΔT ˚K characterizes energy flow through surface; it may be estimated by comparison of the effective surface temperature [68] with the observed one [69] ; Galilean satellite energy flow is estimated as summary of tidal dissipation (Tidal) and internal energy release (Rad) from ( [71] , Table 7.1); Galilean magnetic field according to ( [73] , Table 5).
the power of the main generator for small and big electrical machines correspondingly. Ionosphere electricity causes change in GMF with amplitude about 1% so this value may be used as first approximation.
The exciter field intensity and polarity depends on the ratio of the solidification mass flows in the northern and in the southern hemispheres, which is governed by migration of the solidifications zones. If the ratio is close to one, the intensity of GMF will be close to zero. Predominance of thermo-chemical flows in one hemisphere or the other will dictate GMF’s polarity. Thus a reverse of the main GMF does not need any dramatic change of thermo-chemical flows direction and the corresponding compensation of their inertia. Energy demand for reverse of thermoelectric currents is negligible.
Physicochemical reactions generate ionic currents and thermo-chemical flows connecting anode and cathode zones of solid core and mantle. These flows are deflected by Coriolis forces thus creating the exciting magnetic field. Coriolis forces act in the equatorial zone ±60 latitudes thus determining the main dipole of GMF.
The matter, mainly silicates, of the mantle is an ideal medium for thermoelectricity generation on the all phase boundaries. Thermoelectricity improves heat and matter transport. The spatial orientation of thermoelectric loops always corresponds to external magnetic field because it decreases free energy of the system. It is principally important that thermoelectric loops amplify magnetic field of exciter. Contrary to that, the induced currents always decrease the magnetic field inducing them. The ionosphere currents and magnetic storms are good examples of such an action.
4. Conclusions
The proposed herein thermo-galvanic model of the Earth’s magnetic field, based on the energy of the Earth’s degassing, explains all the observed magnetic field properties. Every point of considerations, including: galvanic phenomena at selective solidification, formation and deflection of thermo-chemical flows, generation of thermoelectricity at heat flow in mantle etc. can be checked or repeated at easily available conditions.
The proposed model suggests the following necessary conditions for the planetary magnetic field generation: 1) running chemical or mechanical processes of the ionic current generation, 2) release of significant heat flows due to degassing, gravitational differentiation and to tidal dissipation, 3) deflection of the thermo-chemical flows due to fast rotation. The proposed model does not contradict any known data.
As it was mentioned in the Section 1, the primordial H- and He-degassing processes are the source of major energy release equal to 5.12 × 1020 J/yr—half of the present rate of the heat flow from the Earth’s surface [23] [24] . The Earth’s degassing is discussed also in: Sandel et al. [76] , report NASA [77] , Gonnermann and Mukhopadhyay [78] , Gonnermann and Houghton [79] and on other planets, for example, on the Mercury, in Herndorn [80] .
Acknowledgements
The author is thankful to Dr. Arie Gilat from the Geological Survey of Israel for very useful discussions and help in preparation of this article.
References
- Condie, K.C. (2011) Earth as an Evolving Planetary System. 2nd Edition, Academic Press, New York, 574 p.
- Gubbins, D. (1972) Kinematic Dynamos and Geomagnetism. Nature Physical Science, 238, 119-122. http://dx.doi.org/10.1038/physci238119a0
- British Geological Survey (2012) The Earth Magnetic Field. Overview of British Geological Service. http://www.geomag.bgs.ac.uk/research/home.html
- Thompson, T. (1998) Geodynamo Theory. And the Matter of the Electric Universe Hypothesis. http://www.tim-thompson.com/geodynamo.html
- Stern, D.P. (2002) A Millennium of Geomagnetism. Reviews of Geophysics, 40, 1-30. http://istp.gsfc.nasa.gov/earthmag/mill_1.htm http://dx.doi.org/10.1029/2000RG000097
- Glatzmaier, G.A. (2002) Geodynamo Simulations—How Realistic Are They? Annual Review. Earth & Planetary Sciences, 30, 237-257. http://dx.doi.org/10.1146/annurev.earth.30.091201.140817
- Vichare, G. and Rajaram, R. (2009) Comparative Study of Models of Earth’s Magnetic Field Derived from Oersted, CHAMP and SAC-C Magnetic Satellite Data. Journal of Indian Geophysical Union, 13, 33-42.
- Herndon, J.M. (2009) Nature of Planetary Matter and Magnetic Field Generation in the Solar System. Current Science, 96, 1033-1039.
- Ofualagba, G. and Ubeku, E.U. (2011) The Analysis and Modelling of a Self-Excited Induction Generator Driven by a Variable Speed Wind Turbine. In: Carriveau R., Ed., Fundamental and Advanced Topics in Wind Power, InTech. http://dx.doi.org/10.5772/18159
- Sohre, J.S. and Nippes, P.I. (1978) Electromagnetic Shaft Currents and Demagnetization on Rotors of Turbines and Compressors. Proceedings of the 7th Turbomachinery Symposium, College Station, 6-8 December 1977.
- Sohre, J.S. (1995) Shaft Riding Brushes to Control Electric Stray Currents. http://turbolab.tamu.edu/proc/turboproc/T20/T2063-75.pdf
- Vol, A.A. (1988) Research of Shaft Currents Self-Excitation Conditions and Electro-Erosion in Steam Turbines. Transactions of Central Boiler and Turbine Institute, Leningrad, 245, 56-65. (in Russian)
- Safonov, L., Vol, A., Malev, V. and Alfeev, A. (1986) Electro-Erosion of Turbines. Teploenergetika, 6, 20-23. (in Russian)
- Kirschner, J. and Moon, S. (2010) An Investigation of the Homopolar Generator: Determining the Impact of System Characteristics on Efficiency. Electromagnetism: A Modeling and Simulation Approach. Project 2: Final Paper.
- Jones, C.A., Boronski, P., Brun, A.S., Glatzmaier, G.A., Gastine, T., Miesch, M.S. and Wicht, J. (2011) Anelastic Convection-Driven Dynamo Benchmarks. Icarus, 216, 120-135. http://dx.doi.org/10.1016/j.icarus.2011.08.014
- Olson, P.L., Glatzmaier, G.A. and Coe, R.S. (2011) Complex Polarity Reversals in a Geodynamo Model. Earth and Planetary Science Letters, 304, 168-179. http://dx.doi.org/10.1016/j.epsl.2011.01.031
- Herndon, J.M. (2011) Geodynamic Basis of Heat Transport in the Earth. Current Science, 101, 1440-1450. http://www.currentscience.ac.in/Volumes/101/11/1440.pdf
- Kays, W., Crawford, M. and Weigand, B. (2004) Convective Heat and Mass Transfer. 4th Edition, McGraw-Hill Professional, New York.
- Ganapathy, V. (1998) Boiler Circulation Calculations. Hydrocarbon Processing, January 1998, 101-105.
- International Atomic Energy Agency (2005) Natural Circulation in Water Cooled Nuclear Power Plants. Phenomena, Models, and Methodology for System Reliability Assessments. IAEA-TECDOC-1474, Vienna.
- Gauthier-Lafaye, F. (1997) The Last Natural Nuclear Fission Reactor. Nature, 387, 337. http://dx.doi.org/10.1038/387337a0
- Gauthier-Lafaye, F. (2006) Time Constraint for the Occurrence of Uranium Deposits and Natural Nuclear Fission Reactors in the Paleoproterozoic Franceville Basin (Gabon). Geological Society of America Memoirs, 198, 157-167.
- Gilat, A. and Vol, A. (2005) Primordial Hydrogen-Helium Degassing, an Overlooked Major Energy Source for Internal Terrestrial Processes. HAIT Journal of Science and Engineering B, 2, 125-167.
- Gilat, A. and Vol, A. (2012) Degassing of Primordial Hydrogen and Helium as the Major Energy Source for Internal Terrestrial Processes. Geoscience Frontiers, 3, 911-921. http://www.sciencedirect.com/science/article/pii/S1674987112000412
- Marsh, B.D. (1995) Solidification Fronts and Magmatic Evolution. The 1995 Hallimond Lecture. http://www.minersoc.org/pages/Archive-MM/Volume_60/60-398-5.pdf
- Buffett, B.A. (2010) The Enigmatic Inner Core. Science, 328, 982-983. http://dx.doi.org/10.1126/science.1190506
- Deuss, A., Irving, J.C.E. and Woodhouse, J.H. (2010) Regional Variation of Inner Core Anisotropy from Seismic Normal Mode Observations. Science, 328, 1018-1020. http://dx.doi.org/10.1126/science.1188596
- Monnereau, M., Calvet, M., Margerin, L. and Souriau, A. (2010) Lopsided Growth of Earth’s Inner Core. Science, 328, 1014-1017. http://dx.doi.org/10.1126/science.1186212
- Mattesini, M., Belonoshko, A.B., Buforn, E., Ramírez, M., Simak, S.I., Udías, A., Mao, H.K. and Ahuja, R. (2010) Hemispherical Anisotropic Patterns of the Earth’s Inner Core. Proceedings of the National Academy of Sciences of the United States of America, 107, 9507-9512. http://dx.doi.org/10.1073/pnas.1004856107
- Zhang, Y.G. and Yin, Q.Z. (2012) Carbon and Other Light Element Contents in the Earth’s Core Based on First-Prin- ciples Molecular Dynamics. Proceedings of the National Academy of Sciences of the United States of America, 109, 19579-19583.
- Ricolleau, A., Fei, Y.W., Corgne, A., Siebert, J. and Badro, J. (2011) Oxygen and Silicon Contents of Earth’s Core from High Pressure Metal-Silicate Partitioning Experiments. Earth and Planetary Science Letters, 310, 409-421.
- Tsuno, K., Frost, D.J. and Rubie, D.C. (2013) Simultaneous Partitioning of Silicon and Oxygen into the Earth’s Core during Early Earth Differentiation. Geophysical Research Letters, 40, 1-5.
- Karato, S. (1999) Seismic Anisotropy of the Earth’s Inner Core Resulting from Flow Induced by Maxwell Stresses. Nature, 402, 871-873.
- Robertson, W.M. (1966) Propagation of a Crack Filled with Liquid Metal. Transactions of the Metallurgical Society of AIME, 236, 1478-1482.
- Glickman, E.E. (2000) Mechanism of Liquid-Metal Embrittlement by Simple Experiments: From Atomistic to Life- Time. In: Lepinoux, J., et al., Eds., Multiscale Phenomena in Plasticity, NATO ASI Series, Kluwer Academic Publishers, Dortrecht, 383-401.
- Glickman, E. (2011) Dissolution-Condensation Mechanism of SCC in Liquid Metals: Driving Forces and Crack Kinetics. Metallurgical and Materials Transactions A, 42, 250-266. http://dx.doi.org/10.1007/s11661-010-0429-6
- Glickman, E.E. (2002) Short Stripe Effect and Electromigration Stress. Microelectronic Engineering, 64, 383-389.
- Juzeliúnas, E. and Hinken, J.H. (2000) A SQUID Study of Magnetic Fields Induced by the Metal-Liquid Interface. Electrochimica Acta, 45, 3453-3459. http://dx.doi.org/10.1016/S0013-4686(00)00414-X
- Keondjan, V.P. (1981) On the Mechanism of the Gravitational Differentiation in the Inner Earth. In: O’Connell, R.J. and Fyfe, W.S., Eds., Evolution of the Earth, Geodynamics Series, Vol. 5, AGU, Washington DC, 167-195. http://dx.doi.org/10.1029/GD005p0167
- Kohlstedt, D.L. and Holtzman, B.K. (2009) Shearing Melt out of the Earth: An Experimentalist’s Perspective on the Influence of Deformation on Melt Extraction. Annual Review of Earth and Planetary Sciences, 37, 561-593. http://dx.doi.org/10.1146/annurev.earth.031208.100104
- Parmentier, E.M. (1981) A Possible Mantle Instability Due to Superplastic Deformation Associated with Phase Transitions. Geophysical Research Letters, 8, 143-146. http://dx.doi.org/10.1029/GL008i002p00143
- Aubert, J., Amit, H., Hulot, G. and Olson, P. (2008) Thermochemical Flows Couple the Earth’s Inner Core Growth to Mantle Heterogeneity. Nature, 454, 758-761.
- Helge Gonnermann-Research. Overview. www.soest.hawaii.edu/GG/SYI/helge/research.pdf
- Gonnermann, H.M., Jellinek, A.M., Richards, M.A. and Manga, M. (2004) Modulation of Mantle Plumes and Heat Flow at the Core Mantle Boundary by Plate-Scale Flow: Results from Laboratory Experiments. Earth and Planetary Science Letters, 226, 53-67. http://dx.doi.org/10.1016/j.epsl.2004.07.021
- Jellinek, A.M., Gonnermann, H.M. and Richards, M.A. (2002) Plume Capture by Divergent Plate Motions: Implica- tions for the Distribution of Hotspots, Geochemistry of Mid-Ocean Ridge Basalts, and Estimates of the Heat Flux at the Core-Mantle Boundary. Earth and Planetary Science Letters, 205, 361-378. http://dx.doi.org/10.1016/S0012-821X(02)01070-1
- Gonnermann, H.M. and Mukhopadhyay, S. (2009) Preserving Noble Gases in a Convecting Mantle. Nature, 459, 560-563. http://dx.doi.org/10.1038/nature08018
- Gufeld, I.L. and Matveeva, M.I. (2011) Barrier Effect of Degassing and Destruction of the Earth’s Crust. Doklady Earth Sciences, 438, 677-680.
- Gufeld, I.L., Gusev, G.A., Lyutikov, R.A. and Matveeva, M.I. (1999) Seismic Process as Phase Instability of Lithosphere. In: Hayakawa, M., Eds., Atmospheric and Ionospheric Electromagnetic Phenomena Associated with Earthquakes, Terra Scientific Publishing Co., Tokyo, 885-909.
- Persson, A.O. (2005) The Coriolis Effect: Four Centuries of Conflict between Common Sense and Mathematics. History of Meteorology, 2, 1-24.
- Aubert, J., Finlay, C.C. and Fournier, A. (2013) Bottom-Up Control of Geomagnetic Secular Variation by the Earth’s Inner Core. Nature, 502, 219-223. http://dx.doi.org/10.1038/nature12574
- Sreenivasan, B. and Jellinek, A.M. (2012) Did the Tharsis Plume Terminate the Martian Dynamo? Earth and Planetary Science Letters, 349-350, 209-217. http://dx.doi.org/10.1016/j.epsl.2012.07.013
- Prior, C.R. (2012) Electromagnetism. ASTeC Intense Beams Group. Rutherford Appleton Laboratory. Fellow and Tutor in Mathematics. http://cas.web.cern.ch/cas/Baden/PDF/Electromagnetism-2.pdf
- Moffat, H.K. (1994) The Earth’s Dynamo. In: Lynden-Bell, D., Ed., Cosmical Magnetism, Springer, the Netherlands, 1-10, 215 p. http://link.springer.com/book/10.1007/978-94-011-1110-2
- The Magnetic Field of the Earth-MIT. http://www-gpsg.mit.edu/12.201_12.501/BOOK/chapter3.pdf
- Goupil, C., Seifert, W., Zabrocki, K., Müller, E. and Snyder, G.J. (2011) Thermodynamics of Thermoelectric Pheno- mena and Applications. Entropy, 13, 1481-1517. http://dx.doi.org/10.3390/e13081481
- Rötzer, G., Lockwood, L., Gil, Z. and Jose, L. (1977) Measurement of Thermopelectric Coefficients at the Solid-Liquid Interface of Highly Doped p-Type Silicon. Journal of Applied Physics, 48, 750-753.
- Mayer, P.M. and Ram, R.J. (2006) Optimization of Heat Sink-Limited Thermoelectric Generators. Nanoscale and Microscale Thermophysical Engineering, 10, 143-155. http://dx.doi.org/10.1080/10893950600643063
- Zheng, R.T., Gao, J.W., Wang, J.J. and Chen, G. (2010) Reversible Temperature Regulation of Electrical and Thermal Conductivity Using Liquid-Solid Phase Transitions. Nature Communications, 2, 289. http://dx.doi.org/10.1038/ncomms1288
- Russell Humphreys, D. (2002) The Earth’s Magnetic Field Is Still Losing Energy. Creation Research Society Quarterly Journal, 39, 1-11.
- Davies, J.H. and Davies, D.R. (2010) Earth’s Surface Heat Flux. Solid Earth, 1, 5-24. http://www.solid-earth.net/1/5/2010/se-1-5-2010.pdf http://dx.doi.org/10.5194/se-1-5-2010
- Dethloff, C., Gaganidze, E., Svetukhin, V.V. and Aktaa, J. (2012) Modeling of Helium Bubble Nucleation and Growth in Neutron Irradiated Boron Doped RAFM Steels. Journal of Nuclear Materials, 426, 287-297. http://dx.doi.org/10.1016/j.jnucmat.2011.12.025
- Gaganidze, E., Petersen, C., Materna-Morris, E., Dethloff, C., Weiß, O.J., Aktaa, J., Povstyanko, A., Fedoseev, A., Makarov, O. and Prokhorov, V. (2011) Mechanical Properties and TEM Examination of RAFM Steels Irradiated up to 70 dpa in BOR-60. Journal of Nuclear Materials, 417, 93-98. http://dx.doi.org/10.1016/j.jnucmat.2010.12.047
- Zhang, P.B., Zhao, J.J., Qin, Y. and Wen, B. (2011) Stability and Dissolution of Helium-Vacancy Complexes in Vanadium Solid. Journal of Nuclear Materials, 419, 1-8.
- Liberman, M.A., Ivanov, M.F., Kiverin, A.D., Kuznetsov, M.S., Chukalovsky, A.A. and Rakhimova, T.V. (2010) Deflagration-to-Detonation Transition in Highly Reactive Combustible Mixtures. Acta Astronautica, 67, 688-701.
- NASA (2013) Planetary Fact Sheet-Metric. http://nssdc.gsfc.nasa.gov/planetary/factsheet/
- Galilean Satellite Fact Sheet. http://nssdc.gsfc.nasa.gov/planetary/factsheet/galileanfact_table.html
- Anderson, B.J., Johnson, C.L., Korth, H., Purucker, M.E., Winslow, R.M., Slavin, J.A., Solomon, S.C., McNutt Jr., R.L., Raines, J.M. and Zurbuchen, T.H. (2011) The Global Magnetic Field of Mercury from MESSENGER Orbital Observations. Science (American Association for the Advancement of Science), 333, 1859-1862. http://dx.doi.org/10.1126/science.1211001
- Barton Paul Levenson. Effective Temperature. http://bartonpaullevenson.com/Albedos.html
- Bob Alien. Planetary Statistics Table-Bob the Alien’s Tour of the Solar System. www.bobthealien.co.uk/table.htm
- (2014) Sources and Movement of Heat within Planets. GEOL212: Planetary Geology Fall 2014. http://www.geol.umd.edu/~jmerck/geol212/lectures/10.html
- Collins, G.C., McKinnon, W.B., Moore, J.M., Nimmo, F., Pappalardo, R.T., Prockter, L.M. and Schenk, P.M. (2009) Tectonics of the Outer Planet Satellites. Ch. 7. In: Watters, T.R. and Schultz, R.A., Eds., Planetary Tectonics, Cambridge University Press. http://www.es.ucsc.edu/~fnimmo/website/icy_satellite_tectonics.pdf
- Bagenal, F. (1992) Giant Planet Magnetospheres. Annual Review of Earth and Planetary Sciences, 20, 289-328. http://dx.doi.org/10.1146/annurev.ea.20.050192.001445
- Cebron, D., Le Bars, M., Moutou, C. and Le Gal, P. (2012) Elliptical Instability in Terrestrial Planets and Moons. Author Manuscript. Astronomy and Astrophysics, 539, 16". http://hal.archives-ouvertes.fr/docs/00/67/67/05/PDF/Cebron_telluric.pdf
- Kivelson, M.G., Khurana, K.K. and Volwerk, M. (2002) The Permanent and Inductive Magnetic Moments of Ganymede. Icarus, 157, 507-522. http://dx.doi.org/10.1006/icar.2002.6834
- Nimmo, F. and Watters, T.R. (2004) Depth of Faulting on Mercury: Implications for Heat Flux and Crustal and Effective Elastic Thickness. Geophysical Research Letters, 31, L02701. http://dx.doi.org/10.1029/2003GL018847
- Sandel, B.R., Goldstein, J., Gallagher, D.L. and Spasojevic, M. (2003) Extreme Ultraviolet Imager Observations of the Structure and Dynamics of the Plasmasphere. Space Science Reviews, 109, 25-46. http://dx.doi.org/10.1023/B:SPAC.0000007511.47727.5b
- Space Weather Camera Set for Launch in 2000. http://science.nasa.gov/science-news/science-at-nasa/1999/ast16feb99_1/
- Gonnermann, H.M. and Mukhopadhyay, S. (2007) Non-Equilibrium Degassing and a Primordial Source for Helium in Ocean-Island Volcanism. Nature, 449, 1037-1040. http://dx.doi.org/10.1038/nature06240
- Gonnermann, H.M. and Houghton, B.F. (2012) Magma Degassing during the Plinian Eruption of Novarupta, Alaska, 1912. Geochemistry, Geophysics, Geosystems, 13.
- Herndon, J.M. (2012) Hydrogen Geysers: Explanation for Observed Evidence of Geologically Recent Volatile-Related Activity on Mercury’s Surface. Current Science, 103, 361-362.






