Open Journal of Applied Sciences
Vol.05 No.12(2015), Article ID:62512,16 pages
10.4236/ojapps.2015.512082
An Expansion of Boundary Theory and the Application of Joint Condition
R. Song1,2*, S. X. Wu3
1Springer Publishing Company, Germany
2Ethan Publishing Company, Rowland Heights, USA
3Self-Employed (Engineer)

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 October 2015; accepted 28 December 2015; published 31 December 2015
ABSTRACT
The manuscript reviews the history and quo of the theory of Timoshenko’s method in stability analysis of compressive levers first, taking an example to explain the m-simulation method and putting forward the 3rd-7th boundary conditions demonstrating their superiorities in improving the precision through examples, followed by proposing and applying the join conditions in the stability analysis of combined axial force compressive levers gaining success. Through a brief example showing the effect of some related theories in a simple structural stability analysis, its application prospect is discussed.
Keywords:
Stability Analysis, Energy Method, BC. (Abbreviation of Boundary Condition), m-Simulation Method, y(n)-Simulation Method, Trial Function, JC. (Abbreviation of Join Condition)

1. Introduction
As is known, the exact static method in structural stability analysis is difficult to push the popularization for the huge calculation amount etc. making the energy method of approximation including several simulated deformation method ([1] , pp. 88-91), gaining highly regarded for the calculation being relatively simple. Among them, the Timoshenko’s method [2] [3] , also called the single-parameter method [4] [5] , the energy method of generalized single degree of freedom [6] or simply the energy method [7] -[9] , becomes the most popular to improve the complexity and limitations of the static method, promoting the popularization of the stability analysis theory. Although in the recent years, the advent of a software called the matrix displacement method ( [8] , pp. 188-200), being available in almost all kinds of structures obtaining results with enough precise, the teaching material of higher education involving the stability analysis, however, had no fundamental changed. The author thought that too much input workload may be one of the main reasons making the energy method become the most important content of the stability analysis in the teaching material. In order to ensure the precision, Timoshenko emphasized that the lever, as an issue of single degree of freedom, the deformation function in critical state should at least satisfy the (end) conditions pertaining to deflections and slopes ( [1] , p. 88), hereinafter called the first and second BC.s. However, in order to obtain higher precision, the energy method calculation has to go from one degree of freedom to multiple degrees of freedom making the calculation amount increase greatly [3] -[7] . In order to improve this situation, two methods designing the deformation function with mathematical and mechanical techniques were put forward in 2006 ( [9] , pp. 127-129). On the premise of guarantee of the accuracy, the application range of the single degree deformation function had been widened to various types of compressive levers. Based on the mechanical method, the m-simulation method was put forward there ( [9] , pp. 141-157) too, not only further simplifies the calculation, but also makes the application range expanding to frame structures; a convenient and practical exe software had also been developed successfully ( [9] , pp. 280-286).
The accuracy of the m-simulation method depends on the degree of the designed m-curve approaching to the critical state of the object. The author found in practice that in addition to the 2 BC.s put forward by Timoshenko, some other relative values on certain specific sections in the lever could also be predetermined with qualitative even quantitative; thus, they could be made use in designing the trial function
 (see next section); so the degree of the function approaching to the critical state could also be improved and the precision would be enhanced as well. In the other words, the y-designing in the energy method would expands to
(see next section); so the degree of the function approaching to the critical state could also be improved and the precision would be enhanced as well. In the other words, the y-designing in the energy method would expands to
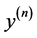 -designing including the m-designing as
-designing including the m-designing as . Thus, the stability analysis would present diversity from which the best result could be picked according to the nature of the lower limit of the energy method―considering the true one as the lower limit, as narrated in ( [1] , p. 90): the critical load becomes larger than the true one. At the same time, it also makes the contradiction between accuracy and computational cost balance at a higher level.
. Thus, the stability analysis would present diversity from which the best result could be picked according to the nature of the lower limit of the energy method―considering the true one as the lower limit, as narrated in ( [1] , p. 90): the critical load becomes larger than the true one. At the same time, it also makes the contradiction between accuracy and computational cost balance at a higher level.
In order to make the text concise and clear, below agreed to use “A ≥ B” instead of “proposition B would be derived from proposition A” and agreed upon in the formula that “l” to be the length measurement of the lever; “z” to be a variable with no dimension and “x” to be the one with the dimension of length; that is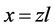 ; then “a” to be a micro const with the dimension of moment.
; then “a” to be a micro const with the dimension of moment.
2. The Revelation of m-Simulation Method, the Boundary Condition Expansion and the Concept of y(n)-Simulation Method
For the convenience in reading comprehension, it is necessary to review the basic principle of m-simulation method especially for the English readers as it is narrated in Chinese ( [9] , pp. 141-157).
As is known, the theory of energy method comes from the principle of minimum potential energy, namely
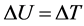 ( [1] , p. 84) (1)
( [1] , p. 84) (1)
In the presence of prismatic cantilever column at the top of compression, using
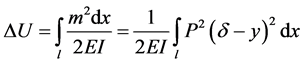 ( [1] , p. 90) (1-A)
( [1] , p. 90) (1-A)
Or
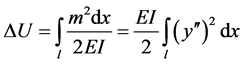 ( [1] , p. 90) (1-B)
( [1] , p. 90) (1-B)
And
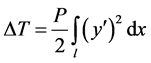 ( [1] , p. 93) (1-C)
( [1] , p. 93) (1-C)
The formula calculating the critical load of the pressure P on the top of the lever could be driven respectively as≥ (2-A)
(2-A)
Or
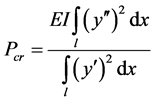 ( [1] , p. 93) (2-B)
( [1] , p. 93) (2-B)
Although the more precision result could be calculated with formula (2-A) ( [1] , p. 89) than that with (2-B) (
[1] , p. 89) than that with (2-B) (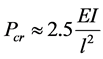 [1] , p. 89), the large amount of calculation and the restricted of application range
[1] , p. 89), the large amount of calculation and the restricted of application range
(only the prismatic cantilever column with a pressure on the top), restricted (2-A) of popularization. On the contrary, formula (2-B) has spread around the world such as the literatures of references [2] -[9] . On the premise of small deformation and linear elastic, taking note of
 and
and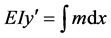 , (2-B) becomes
, (2-B) becomes
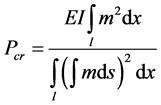 ( [9] , p. 141) (3-A)
( [9] , p. 141) (3-A)
Making the result be determined by the unique function m; thus the y-designing in (2-B) could be replaced by the m-designing in (3-A). For the function m is a simulation of the critical state, it is called the m-simulation method ( [9] , p. 141).
In case of several axial loads or ladder cross-section levers, (3-A) becomes

(EIS is a representative value selected from

Besides can easily satisfy the 2 BC.s suggested by Timoshenko ensuring an accuracy of certain degree, the application of m-simulation method also simplifies the calculation and reveals the direction for the boundary theory developing as well, see the example below.
Example 1
A pressure lever as Figure 1(a), calculate the critical load

Method 1: Choose the simulation m-curve as Figure 1(b),
That is



BC.2 on A (see Table 1 in the next section):


Taking (3-A) gives

The error is about 1.3% comparing with the exact solution

a good precision, in addition to the method satisfies the 2 BC.s put forward by Timoshenko, it satisfies the volume of 0, the moment at the top, as well, hereinafter referred to as the 3rd BC.: See Table 1 in the next section.
Method 2: Choose the m curve as Figure 1(c), that is





Figure 1. Several figures of schemes for the m-simulation method in example 1.
Method 3: Take the simulation m curve as Figure 1(d) that



The error is about 0.13%; the precision is about 10 times higher than that of method 1. Obviously, in addition to the main reason satisfying the 3 BC.s mentioned in method 1, it satisfies BC. 4 also, see Table 1 in the next section and verify it please.
Method 4: Choose


Due to the chosen m-curve is exactly the same with that of the lever in critical state; the results are the same also.
Discussion: Although the m-simulation method has certain guarantee of accuracy, the above methods of 1 and 2 satisfying all the first 3 BC.s mentioned, made different errors, some one even larger than 10%, such as method 2. However, the accuracy of method 3 and 4 are very high, this is because they not only satisfy the first 3 BC.s, but also satisfy the shear at the bottom section, the 4th BC. on A being 0 as well, see Table 1. More so, method 4 got the exact result with energy method; the reason is that the designed m-curve is perfectly the same with the lever in critical state. Although no exact solution of specific case, the probability of the basic is zero, we can still find some clues from the existing results, such as the m-curve in method 3 and 4 are very similar, the difference of the results comes from the difference of the 5th-6th BC.s, see Table 1. If these BC.s would be sa-
tisfied, a more accuracy of energy method with the trial function different from

Method 5: Choose




The error is about 0.014% and the accuracy increased significantly about 10 times as that of method 3. Obviously, the main reason is that the designed trial function satisfies all the fist 5 BC.s mentioned; verify it please.
Method 6: In order to satisfy all the first 6 BC.s in Table 1,
Suppose



BC.5:


BC.4:


BC.3:


BC.2:


The error is about 0.00017%, more than 80 times as accurate comparing with method 5.
Brief summary:
Despite of method 4 gives the exact solution; the trigonometric trial function would not be discussed below (see the section under). In all the others except method 4, the most accurate result belongs to method 6, for all the BC.s for Lever 1 in Table 1 are satisfied. You may have also found that about this example, the same designed
deformation function of

of (2-A) and (2-B) gaining different results and the one with (2-A) getting more accurate. The reason is that different methods were applied in calculating the function of m: the former add the load on the assumed curve calculating the m-function with static method; whereas the latter obtained the m-function applying the differential relationship of


The method 6 in the above example would not be called the m-simulation method being not begins from supposing the function m; as it makes more convenience, it is recommended here and would be called the

3. A Collection and Introduction of 7 BC.s and Their Primary Application to Lever 2―y(n)-Simulation Method
We can see from example 1 that the




3.1. The Introduction and Application of All the 7 BC.s in Stability Analysis for L2―y(n)-Simulation Method
As mentioned earlier, there are many BC.s at some specific sections in a prismatic compressive cantilever; they will be introduced in Table 1.
3.2. The Application of All the 7 BC.s in the Stability Analysis to Lever 2
The stability analysis for Lever 2 is taken as one of the most classic example in the course of energy method for stability analysis in multiple versions of textbook [1] -[8] . Example 2 below would show you the advantage of making full use of the 7 BC.s in the analysis.
Example 2
A prismatic cantilever as in Figure 2(a), with uniform distribution dead load of q, analyze the critical value of it (the difference between q and

Analysis
As the gravity q is the only factor considered in the stability analysis, formula (2-A) or (2-B) could not be applied directly. The result should be gained by formula (1).
Method 1 Take the deflection curve as


Comparing with the exact result

Table 1. The introduction for all the 7 BC.s in a prismatic cantilever (Lever 1 considers the top load P only, yet Lever 2 considers the own weight q only; the corresponding physical quantities are also indicated by

Brief summary: The above table providing 6 and 7 BC.s for Lever 1 and Lever 2 respectively. For the application to Lever 1 has been introduced in section 1, below will introduce their application to Lever 2 only.
Method 2 Take the deflection curve as

Then

and

Equaling



terature [4] -[6] , but the result given in literature [3] [7] is


the first 3 BC.s are satisfied, the accuracy is poor. Yet, the calculation is much simpler than that in method 1.

Figure 2. Several figures of schemes for y(n)-simulation method in example 2.
Method 3 Due to the load uniformly distributed along the stem, it is not difficult to find in critical situation, that the shear at the top and bottom sections are all 0 (being called BC.4, see Table 1). So take the m-curve as Figure 2(b), the superposition of Figure 2(b1) and Figure 2(b2); Figure 2(b1) is a straight line with the function

bottom sections being all 0. For the corresponding slope in Figure 2(b1) is

Making



That is


BC. on A:



Equaling




the error is about 0.36%. Not only improved the precision greatly and simplify the calculation comparing with the one in method 1 and 2. We can see that BC.4 has a great impact to the result.
Method 4 According BC.4, we can also suppose


BC. on B:

As the m- function has the same variable factor of

Method 5 Suppose


BC. on A:

BC. on B:

BC. on A:

Then

And

Equaling



Comparing with exact one
thod 3 (4). So there is good effect, satisfy all the 7 BC.s is the main reason. It also provides the scope of the
rough of
Method 6 Suppose



In order to meet






BC.4:

BC. on B:

BC. on A:

Then

And

Equaling



Comparing with exact one
comparing with that of method 5. Visible,


In order to simplifying the narrative, the follow methods would omit some steps in calculation, only the key dates would be provided in Table 2 adding method 5 and 6 in order for facilitate in comparison.
Table 2. The related values of 6 methods in example 2, satisfying all the 7 boundary conditions.
Method 11 Suppose



Comparing with the exact solution, the error is about 2.08%. When compare with the traditional method 2 having been incorporated into many versions of textbooks, it improves in both the precision and the amount of calculation greatly.
Brief summary
1) The analysis for 2 kinds of cantilever pressure levers considering only the top load or the own weight are introduced in the above 2 sections. If only considering the precision requirement, it seems to reinvent the wheel, for the exact results had been given by P. Timoshenko in ( [1] , p. 88) more than 50 years ago. The introducing of the 7 BC.s here is to draw some regularity, in order to deal with more complex stability analysis. Generally speaking, the larger number of n (the series number of BC.s satisfied) the higher accuracy will be got; the smaller of the value of n the greater impact of the corresponding BC. will make.
2) There are 11 kinds of methods in example 2 and method 5 - 10 satisfied all the 7 BC.s; the related dada are provided in Table 2. From the calculation results, it seems that the error of the most accuracy should be 0.0056% provided in method 9. Visible, for the precision of energy method, there may be no best, just better (as the exact one may be an irrational).
4. The Application of JC.s and BC.s in Stability Analysis for Combination of Axial Force
The combined axial force compressive lever refers to that with uniform or ladder sections supported loads on multi sections or only on the top being one of the common structure components. In this case, there are certain relationships between some physical quantities on the up and down of the sections loaded, hereinafter called Join Conditions, simply JC.; the precision can be improved in applying them.
In order to simplify the narrative, save for “

4.1. The Stability Analysis for the Prismatic Compressive Levers under the Acting of Combined Axial Forces
The analysis for a lever under the action of 2 loads would be introduced first.
Example 3
Calculate the critical load

Method 1 Suppose the simulative loads as Figure 3(b), then we have:
Upper segment:

Lower segment:

BC. on A:

JC. on C:



By taking formula (3-B), we have



Figure 3. Several figures of schemes for y(n)-simulation method in example 3.
The results of method 2 and 3 are finished by computer and the results of 3 methods are shown in Table 3 below.
4.2. The Stability Analysis for the Ladder Cross-Section Compressive Levers
For the stability analysis of levers with ladder cross-section, many references analyzed with static method
Table 3. The computers results of example 3 (The exact solution:

Brief summary: The precision of method 2 is the highest being with a linear S-simulation function.
[3] -[8] , below will show you the energy method; as long as pay attention to the use of the all kinds of BC.s and JC.s introduced above, the energy method could be used to calculate precision fairly good results.
Example 4
Calculate the critical load

There will show you 3 methods with the trial function of S-simulation function as Figures 4(b)-(d). All the results are calculated by computer (Table 4).

Figure 4. Several figures of schemes for y(n)-simulation method in example 4.
Example 5
Calculate the critical load

5. A Primary Application of the Boundary-Theories in Structure Stable Analysis
Admittedly, how the theory could (directly or indirectly) apply to actual can reflect its value. A brief example
Table 4. The computers results of example 4 (The exact solution:

Brief summary: Obviously the precision of method 2 with linear S-simulation function is the best.

Figure 5. Several figures of schemes for y(n)-simulation method in example 5.
preliminary applying the Boundary theory on a simple structural analysis will be showed below.
Example 6
Calculate the critical loads

Analysis:
In practical engineering, in mechanical analysis, in addition to the precision requirement the simplified calculation is very important to the promotion. Therefore, the first selection algorithm is the most simple m-simula- tion method. As the structure is symmetry, the antisymmetry critical load is lesser; Figure 6(b) would be taken as the calculating diagram. (The origin of coordinates is fixed on the bottom)
Method 1
Suppose the simulation load as Figure 6(c), the m-diagram would be calculated by the method of non-shear
Table 5. The computers results of example 5 (The exact solution:

Brief summary: The above 3 examples show the precision guarantee of applying BC.s and JC.s in the stability analysis for combination of axial force. We can also see that the highest accuracy belongs to the one with linear

distribution as is shown in Figure 6(c), a linear m-curve would be obtained; that is:






Figure 6. The stability for a single-store frame by m-simulation method in example 6.
Method 2
Based on the result of method 1, the m diagram would be adding a cubic parabola as in Figure 6(d),
That is
firmed ( [9] , p. 282).
BC. on C:



Then

This is the result of a straight line adding a cubic parabola. In the above equation, constant

lected automatically by the software designed. Comparing with the exact result
0.49%. Such a simple dealing with (only make the analyzing satisfy the BC. 4, the 0 shear on the bottom section C of the column approximately), that brings the effect of error in half of that in method 1. It indicates the boundary theory of broad application prospects. In addition, the programming is simple, and can be used in the stability analysis of high-rise frame structures and the application of the software is very convenient, especially in input ( [9] , pp. 280-286).
6. Summary
Since 1961, when the Energy Method was put forward by Timoshenko [1] , it got gradually into practical application phase. The 3rd-7th BC.s and JC.s put forward here would improve the precision obviously. The related theory and the high precision trial functions would add some advantage factors for the stability theory to further develop.
In spite of wide application of the matrix displacement method [8] , its input trouble faults are also obvious. Energy method, however, can make up for the shortcomings, and has realized the practical application in [9] . For the software is made out in Chinese identity, the application scope is limited in a certain degree. As the developer of the software, we are trying to translate the software into English as soon as possible and strive for some breakthroughs, in order to provide better service for readers.
In addition, due to the result of author’s subjective and objective limitations, the errors are inevitable; the software also has some defects; so, we sincerely hope readers to give us more criticism and help, especially in such as variety of software development and application of all-round cooperation. We certainly hope this article can cause the reader’s interest, for energy method to expand the application scope, simplify the calculation, improve the precision and so on, and put forward some new more effective method.
Cite this paper
R.Song,S. X.Wu,11, (2015) An Expansion of Boundary Theory and the Application of Joint Condition. Open Journal of Applied Sciences,05,844-859. doi: 10.4236/ojapps.2015.512082
References
- 1. Timoshenko, S.P. and Gere, J.M. (1961) Theory of Elastic Stability. 2nd Edition, McGraw-Hill Book Company, INC., Boston.
- 2. Lee, C.Q. (1999) Structural Stability and Stable Internal Forces. China Communications Press, Beijing. (In Chinese)
- 3. Xiao, Y.H., Zhang, L.Y., Chen, M.D., et al. (1999) Structural Mechanics Part II. China Machine Press, Beijing. (In Chinese)
- 4. Liu, Y.S., Bai, B.S., et al. (2004) Structural Mechanics Part II. Science Press, Beijing. (In Chinese)
- 5. Zhang, L.Y., Jing, R., Zhao, G.X., et al. (1997) Structural Mechanics Part II. China Building Industry Press, Beijing. (In Chinese)
- 6. Bao, S.H., Xin, K.G., et al. (2003) Structural Mechanics Part II. Version 2, Wuhan University of Technology Press, Wuhan. (In Chinese)
- 7. Long, Y.Q., Bao, S.H., et al. (2006) Structural Mechanics Part II. Version 2, Higher Education Press, Beijing. (In Chinese)
- 8. Yuan, S. (2001) Program Structure Mechanics. Higher Education Press, Beijing. (In Chinese)
- 9. Song, R. (2006) Tricks and Procedure in Mechanical Analysis. (In Chinese)
NOTES

*Retied Associate Professor of Wuyi University (China).
















































































