American Journal of Analytical Chemistry
Vol. 3 No. 12A (2012) , Article ID: 26177 , 4 pages DOI:10.4236/ajac.2012.312A125
Extraction and Characterization of Oil from Moringa oleifera Using Supercritical CO2 and Traditional Solvents
1Facultad de Ingenieria Quimica, Universidad Autonoma de Yucatan, Col. Chuburna de Hidalgo Inn, Merida, Mexico
2LODEMO Group, Merida, Mexico
Email: *antonio.rocha@uady.mx
Received October 20, 2012; revised November 21, 2012; accepted November 30, 2012
Keywords: Moringa oleifera; CO2 Supercritical Extraction; Solvent Extraction; Ben Oil
ABSTRACT
The present work presents a first characterization of the oil from the Moringa (Moringa oleifera) kernel as a potential candidate for biodiesel production. Moringa is an indigenous tree in the Yucatan Peninsula in Mexico, where there is a nascent biodiesel industry. Several extraction methods are compared in terms of the extraction yields, including solvent extraction (n-hexane and ethanol), and supercritical extraction (Sc-CO2). The results are also compared against previously reported data. For supercritical extraction pressures of 200 to 400 bar and temperatures of 40˚C and 60˚C were tested. Gas Chromatography analysis reveals that the main fatty acids in Moringa oil are oleic acid (69%), palmitic acid (10%) and stearic acid (8%).
1. Introduction
Moringa oleifera, known as “Moringa” or “Malunggay” is an Indian tree that also grows in Asia, Africa, Southamerica, the Caribbean and Oceania. The oil extracted from Moringa is known as Ben oil and reportedly contains 70% of oleic acid, an 18-carbon long monounsaturated fatty acid (MUFA). Since the oleic acid has good oxidative stability when compared with polyunsaturated fatty acids (PUFAs), it has found use in the food industry, as it allows for longer storage and high-temperature frying processing. It also has uses in medicine and water treatment.
According with Abdulkarim et al. [1] Ben oil is more stable than canola oil, soybean oil, and palm oil when used in frying. Blending Ben oil with sunflower oil and soybean oil enhances the oxidative stability of the mixture. Mani et al. [2] say that comparing its chemical properties, Moringa seed oil is considered equivalent to olive oil, and may be used for human consumption. Also, the oil from Moringa seeds has shown the strongest antifungal activity against a zoophilic dematophyte caused marked inflammatory reactions in humans [3].
Another potential use of Moringa oil is as biodiesel feedstock. Currently, there is a nascent biodiesel industry in the Yucatan Peninsula, Mexico, that has been active for the last 2 - 3 years. Several groups are trying to obtain biodiesel from vegetable oils, especially Jatropha curcas, and from waste cooking-oil. As an alternative source of oil, Moringa seeds have been proposed as a potential source to complement the mentioned feedstock.
In this study, experimental results of solvent Soxhlet extraction using n-hexane and ethanol, and supercritical extraction with CO2 are reported. Solvent extraction has been reported by Mani et al. [2] using n-hexane, petroleum ether and acetone. Experimental Soxhlet extraction using n-hexane and ethanol, and also supercritical extraction with CO2 on Moringa seeds have been reported by Nguyen et al. [4]. Extraction of essential oil components using supercritical fluids has received much attention in the past years because it presents an alternative to solvent extraction or steam distillation. Sovova and Stateva [5] recently review the field of supercritical extraction of vegetable materials and say that industrial applications are increasing. It is hoped that the results will provide information to compare Moringa seeds cultivated in Yucatan-Mexico as raw material candidate for vegetable oil and biodiesel.
2. Materials and Methods
2.1. Material and Sample Preparation
Moringa seeds from wild trees in the Yucatan Peninsula, Mexico were used. The seeds shown in Figure 1 were separated from the membranes and milled by three different methods: ball mill, electrical grinder (Moulinex Pikalica), and hand-operated mortar.
Each method resulted in a powder with a size distribution, which was characterized by sieving. The average diameter for supercritical extraction was 0.46 mm and the averaged diameter for solvent extraction was 0.97 mm. The humidity of Moringa oleifera powder was 5. 84% and then do not requires drying.
Supercritical extraction was performed with industrial grade CO2 (99.9%), and dry air was used as the service gas. Both were supplied by Praxair. For the solvent extraction Hexane and ethanol were provided by J. T. Baker.
2.2. Soxhlet and Supercritical Extraction Method
Figure 2(a) shows the Soxhlet apparatus used for solvent extraction (SE) where 10 grams of powder of Moringa oleifera was treated with 210 ml of ethanol or hexane during 6 hours. The solvent was eliminated in a rotavapor and the yield was calculated as grams of extract divided by grams of original powder in a dry basis.
Figure 2(b) shows a photograph of the experimental device for supercritical fluid extraction (SFE). A diagram and procedure is given in [6]. The supercritical extractor is a 0.1 liter cell which is charged with 20 - 30 g of ground Moringa seeds. Each run has 10 minutes of static extraction and 30 minutes of dynamic extraction with a CO2 flow rate of 0.66 g/min.
2.3. Experimental Design
Since at the beginning of the experimental work there were no reports of Moringa seeds extraction using SC-CO2, the extraction conditions recommended for Jatropha curcas [7] oil were used as a starting point. Thus, the rec-

Figure 1. Moringa seeds as collected from the fruit.
 (a)
(a) (b)
(b)
Figure 2. (a) Soxhlet for solvent extraction; (b) Supercritical extraction system SFT-150 by supercritical fluid technologies Inc. Newark, DE, USA.
ommended range of pressure (250 to 350 bar) and temperature (40˚C to 60˚C) was extended, so as to test three pressures (200, 300 and 400 bar), and two temperatures (40˚C and 60˚C).
2.4. GC Analysis
After each extraction, 0.05 g of oil was analyzed using Gas Chromatography/Mass Spectrometry, following the procedure of saponification and derivation recommended by Damiani et al. [8]. The equipment was an Agilent Chromatograph 6890 N and Mass spectrograph Agilent 5973 e. The derivatized samples were injected (1 µl) with a ratio split 50:1 into an Agilent HP-5 GC column (5%- phenyl-methylpolysiloxane, 30 m × 0.32 mm i.d., 0.25 µm). The carrier gas was He at a volumetric flow rate of 1.1 ml·min–1. The temperature was increased 25˚C min–1 from 140˚C to 190˚C, after 1 min it was increased to 240˚C at 4˚C min–1 and kept constant for 15 min.
3. Results and Duscussion
3.1. Experimental Data
Yield was defined as grams of extracted oil divided by grams of seeds charged in cell.
The results obtained for solvent extraction of Moringa oil are shown in Figure 3. Data of Mani et al. [2] is included.
It is seen that ethanol is a better solvent than hexane, petroleum ether and acetone, and that size reduction with the ball mill improve extraction 24% with respect to the use of mortar.
The result of supercritical extraction with an averaged mass flow rate of 0.66 g/min of CO2 is shown in Figure 4.
It is observed that pressure has a direct effect over yield. An increase in pressure at constant temperature acts increasing the density of the supercritical solvent and enhancing the extraction yield reached. For temperature there are two opposite effects: at low values of pressure, an increase in temperature augments the vapor pressure of the components to be extracted and then pressure and yield tend to increase; At higher pressure an increase in temperature decrease the density of the solvent CO2 and the extraction yield decrease.
3.2. Comparison with Other Report
Nguyen et al. [4] report yields higher of 30% for a cell of 500 cm3 with a flow rate of CO2 of 0.5 m3/h or 0.45 kg/h (7.5 g/min) working seven hours. These yields are much higher than those reported in Figure 4 of maximum 2% for 30 minutes. The runs reported here were performed in a cell of 100 cm3 with a flow rate of 0.66 g/min and with only 30 minutes of duration.
3.3. Kinetic Study
The experimental conditions that showed the best yield after 30 min of Sc-CO2 extraction (2% yield, at P = 403 bar, T = 40˚C) were chosen to perform a kinetic run for 7
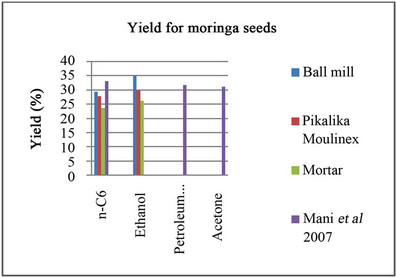
Figure 3. Yields of Soxhlet extraction with different solvents.

Figure 4. Supercritical extraction of Moringa seeds with CO2.
hours and the maximum yield was only 2.8. the results are shown in Figure 5.
It seems that the lower flow rate of CO2 is the cause of the lower yield.
According with Rosa and Meireles [9] a kinetic curve will be necessary to perform an estimate of cost of fabriccation.
The calculation of manufacturing cost for Moringa oil could be used to evaluate its economical feasibility.
3.4. Fatty Acid Composition
Figure 6 presents the content of the main fatty acids (expressed as percentage of total fatty-acids in the oil) measured by GC/MS, for solvent extraction and Sc-CO2 and compares it with data of Nguyen et al. [4]. It is observed that oleic acid, palmitic acid, and stearic acid are the main fatty acids present.
In this case the yield obtained with SFE (8.5%) is lower than SE (23% - 35%) but Nguyen et al. [4] obtained yields of 37%. A comparison between supercritical fluid extraction, solvent extraction and screw press extraction for the extraction of oil from flaxseeds is given by Chandra Pradhan et al. [10]. The main differences are presented in Table 1.
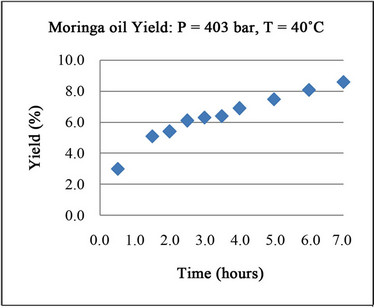
Figure 5. Kinetics run for Moringa seeds with CO2.
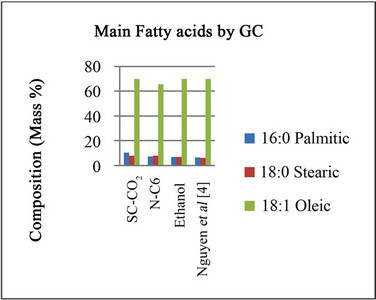
Figure 6. Relative ratio composition of the three more important fatty acids in extracted Moringa oil.
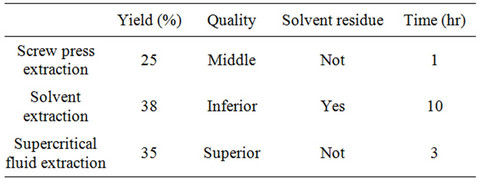
Table 1. Comparison on extraction methods for oil extraction from flax seed. Pradhan et al. 2010.
From Table 1 and experience the main advantages of solvent extractions are: Better yield and economic profits for many industrial commercializations. Its main disadvantages are: organic residual in final oil, high use of energy to recovery and recycle the solvent.
Advantages for supercritical extraction with CO2: clean oil and sustainable process. Main disadvantages: Higher cost and new process.
4. Conclusions
The extraction of oil from Moringa seeds may be carried out by solvent extraction and supercritical extraction with CO2.
Although in this study the yield obtained was low moringa seeds are a good source for oil rich in oleic acid that could be transformed in bio-fuel.
Additional economical and sustainability studies should be performed to select the optimal process.
5. Acknowledgements
The authors gratefully acknowledge the financial support received from LODEMO group and the help of Jose Maria Diaz de la Fuente and Erik Antonio Figueroa Coronel at FIQ-UADY.
REFERENCES
- S. M. Abdulkarim, K. Long, O. M. Lai, S. K. S. Muhammad and H. M. Ghazali, “Frying Quality and Stability of High-Oleic Moringa oleifera Seed Oil in Comparison with Other Vegetable Oils,” Food Chemistry, Vol. 105, No. 4, 2007, pp. 1382-1389. doi:10.1016/j.foodchem.2007.05.013
- S. Mani, S. Jaya and R. Vadivambal, “Optimization of Solvent Extraction of Moringa (Moringa oleifera) Seed Kernel Oil Using Response Surface Methodology,” Food & Bioproducts Processing: Transactions of the Institution of Chemical Engineers Part C, Vol. 85, No. 4, 2007, pp. 328-335. doi:10.1016/j.biortech.2005.11.003
- P.-H. Chuang, C.-W. Lee, J.-Y. Chou, M. Murugan, B.-J. Shieh and H.-M. Chen, “Antifungal Activity of Crude Extracts and Essential Oil of Moringa oleifera Lam.,” Bioresource Technology, Vol. 98, No. 1, 2007, pp. 232-236.
- H. N. Nguyen, P. D. Gaspillo, J. B. Maridable, R. M. Malaluan, H. Hinode, C. Salim and H. K. P. Huynh, “Extraction of Oil from Moringa oleifera Kernels Using Supercritical Carbon Dioxide with Ethanol for Pretreatment: Optimization of the Extraction Process,” Chemical Engineering and Processing: Process Intensificationg, Vol. 50, No. 11-12, 2011, pp. 1207-1213. doi:10.1016/j.cep.2011.08.006
- H. Sovová and R. P. Stateva, “Supercritical Fluid Extraction from Vegetable Materials,” Reviews in Chemical Engineering, Vol. 27, No. 3-4, 2011, pp. 79-156.
- J. A. Rocha Uribe, J. I. Novelo Perez, H. Castillo Cahuil, G. Rosado Rubio and C. Guillermo Alcocer, “Extraction of Oil from Chia Seeds with Supercritical CO2,” Journal of Supercritical Fluids, Vol. 56, No. 2, 2011, pp. 174-178. doi:10.1016/j.supflu.2010.12.007
- W.-H. Chen, C.-H. Chen, C.-M. J. Chang, Y.-H. Chiu and D. Hsiang, “Supercritical Carbon Dioxide Extraction of Triglycerides from Jatropha Curcas L. seeds,” Journal of Supercritical Fluids, Vol. 51, No. 2, 2009, pp. 174-180. doi:10.1016/j.supflu.2009.08.010
- M. C. Damiani, C. A. Popovich, D. Constela and P. I. Leonardi, “Lipid Analysis in Haematococcus Plavialis to Assess Its Potential Use as a Biodiesel Feedstock,” Bioresource Technology, Vol. 101, No. 11, 2010, pp. 3801- 3807. doi:10.1016/j.biortech.2009.12.136
- P. T. V. Rosa and M. A. A. Meireles, “Rapid Estimation of the Manufacturing Cost of Extracts Obtaining by Supercritical Fluid Extraction,” Journal of Food Engineering, Vol. 67, No. 1-2, 2005, pp. 235-240. doi:10.1016/j.jfoodeng.2004.05.064
- R. C. Pradhan, V. Meda, P. Kumar Rout, S. Naik and A. K. Dalai, “Supercritical CO2 Extraction of Fatty Oils from Flaxseed and Comparison with Screw Press Expression and Solvent Extraction Process,” Journal of Food Engineering, Vol. 98, No. 4, 2010, pp. 393-397. doi:10.1016/j.jfoodeng.2009.11.021
NOTES
*Corresponding author.

