Journal of High Energy Physics, Gravitation and Cosmology
Vol.02 No.03(2016), Article ID:68687,20 pages
10.4236/jhepgc.2016.23035
Relic Entropy Growth and Initial Big Bang Conditions, as a Subset of Quantum Information
Andrew W. Beckwith
Department of Physics, Chongqing University, Chongqing, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 May 2016; accepted 17 July 2016; published 20 July 2016
ABSTRACT
This paper shows how increased entropy values from an initially low big bang level can be measured experimentally by counting relic gravitons. Furthermore the physical mechanism of this entropy increase is explained via analogies with early-universe phase transitions. The role of Ng’s revised infinite quantum statistics in the physics of gravitational wave detection is acknowledged. Ng’s infinite quantum statistics can be used to show that 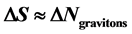 is a starting point to the increasing net universe cosmological entropy. Finally, in a nod to similarities with zero point energy (ZPE) analysis, it is important to note that the resulting
is a starting point to the increasing net universe cosmological entropy. Finally, in a nod to similarities with zero point energy (ZPE) analysis, it is important to note that the resulting 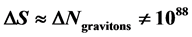 in fact is much lower, allowing for evaluating initial graviton production as an emergent field phenomena, which may be similar to how ZPE states can be used to extract energy from a vacuum if entropy is not maximized. The rapid increase in entropy so alluded to without near sudden increases to 1088 may be enough to allow successful modeling of relic graviton production for entropy in a manner similar to zero point energy (ZPE) energy extraction from a vacuum state. This entropy count is akin to quantum information models used to tell how much “information” may be stored in initial conditions, and transferred from a prior to the present
in fact is much lower, allowing for evaluating initial graviton production as an emergent field phenomena, which may be similar to how ZPE states can be used to extract energy from a vacuum if entropy is not maximized. The rapid increase in entropy so alluded to without near sudden increases to 1088 may be enough to allow successful modeling of relic graviton production for entropy in a manner similar to zero point energy (ZPE) energy extraction from a vacuum state. This entropy count is akin to quantum information models used to tell how much “information” may be stored in initial conditions, and transferred from a prior to the present
Keywords:
Entropy, Cosmic Singularity, Zero Point Energy (ZPE), Emergent Fields, Gravitons, Vacuum States, Quantum Information States, Anti de Sitter Correspondence with Conformal Field Theory, (Ads/CFT)

1. Introduction
We make the following chapter outline which will indicate what models of entropy may work. In addition, a de facto caution as to why string theory models may break down at the cosmic singularity is alluded to. In order to start off this analysis, we begin with the following topics in the chapters, one after the other.
2) Does “Entropy” Have an Explicit Meaning in Astrophysics? i.e. (limitations of the Quark-Gluon analogy and how such limitations impact AdS/CFT correspondence [1] applications. AdS refers to anti-de Sitter (AdS) space in dual to a correspondence with conformal field theory (CFT) which is the linkage implied by AdS/CFT as a dual correspondence linkage.)
3) Ng’s infinite quantum statistics [2] . Is there a linkage of DM and Gravitons?
4) Quantum gas and applications of Wheeler De Witt equation to forming Partition function
5) Brane-antibrane “pairs” and a linkage to Ng’s quantum infinite statistics?
6) Entropy, comparing values from T(u, v) stress energy, black holes, and general entropy values obtainable for the universe.
7) Seth Lloyd’s [3] hypothesis.
8) Simple relationships to consider (with regards to equivalence relationships used to evaluate T(u, v).
9) Data compression, continuity, and Dowker’s [4] space time sorting algorithm.
10) Controversies of Dark Matter and Dark Energy as called by DM/DE applications to cosmology. How High Frequency Gravitational waves (HFGW) may help resolve them.
2. Does “Entropy” Have an Explicit Meaning in Astrophysics?
This paper will assert that there is a possibility of an equivalence between predicted Wheeler De Witt equation early universe conditions and the methodology of string theory, based upon a possible relationship between a counting algorithm for predicting entropy, based upon an article by Jack Ng [1] (which he cites string theory as
a way to derive his counting algorithm for entropy). This is due to re stating as entropy 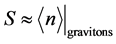 with
with 
as a numerical graviton density and the expression given by Glinka [5] for entropy (where Glinka uses the Wheeler De Witt equation), if we identify 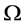 as a partition function due to a graviton-quintessence gas. If confirmed, this may also lead to new ways to model gravity/graviton generation as part of an emergent “field” phenomenon. Now why would anyone wish to revisit this problem in the first place? The reason is because that there are doubts people understand entropy in the first place. As an example of present confusion, please consider the following discussion where leading cosmologists, i.e. Sean Carroll [6] asserted that there is a distinct possibility that mega black holes in the center of spiral galaxies have more entropy, in a calculated sense, i.e. up to 1090 in non dimensional units. This has to be compared to Carroll’s [6] stated value of up to 1088 in non dimensional units for observable non dimensional entropy units for the observable universe. Assume that there are over one billion spiral galaxies, with massive black holes in their center, each with entropy 1090, and then there is due to spiral galaxy entropy contributions
as a partition function due to a graviton-quintessence gas. If confirmed, this may also lead to new ways to model gravity/graviton generation as part of an emergent “field” phenomenon. Now why would anyone wish to revisit this problem in the first place? The reason is because that there are doubts people understand entropy in the first place. As an example of present confusion, please consider the following discussion where leading cosmologists, i.e. Sean Carroll [6] asserted that there is a distinct possibility that mega black holes in the center of spiral galaxies have more entropy, in a calculated sense, i.e. up to 1090 in non dimensional units. This has to be compared to Carroll’s [6] stated value of up to 1088 in non dimensional units for observable non dimensional entropy units for the observable universe. Assume that there are over one billion spiral galaxies, with massive black holes in their center, each with entropy 1090, and then there is due to spiral galaxy entropy contributions 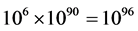 entropy units to contend with, vs. 1088 entropy units to contend with for the observed universe. I.e. at least a ten to the eight order difference in entropy magnitude to contend with. The author is convinced after trial and error that the standard which should be used is that of talking of information, in the Shannon sense, for entropy, and to find ways to make a relationship between quantum computing operations, and Shannon information. Making the identification of entropy as being written as
entropy units to contend with, vs. 1088 entropy units to contend with for the observed universe. I.e. at least a ten to the eight order difference in entropy magnitude to contend with. The author is convinced after trial and error that the standard which should be used is that of talking of information, in the Shannon sense, for entropy, and to find ways to make a relationship between quantum computing operations, and Shannon information. Making the identification of entropy as being written as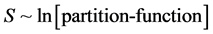 . This is Shannon information theory with regards to entropy, and the convention will be the core of this text. What is chosen as a partition function will vary with our chosen model of how to input energy into our present universe. This idea as to an input of energy, and picking different models of how to do so leading to partition functions models is what motivated research in entropy generation. From now on, there will be an effort made to identify different procedural representations of the partition function, and the log of the partition function with both string theory representations, i.e. the particle count algorithm of Jack Ng, [2] and the Wheeler De Witt version of the log of the partition function as presented by Glinka [5] . Doing so may enable researchers to eventually determine if or not gravity/gravitational waves are an emergent field phenomenon.
. This is Shannon information theory with regards to entropy, and the convention will be the core of this text. What is chosen as a partition function will vary with our chosen model of how to input energy into our present universe. This idea as to an input of energy, and picking different models of how to do so leading to partition functions models is what motivated research in entropy generation. From now on, there will be an effort made to identify different procedural representations of the partition function, and the log of the partition function with both string theory representations, i.e. the particle count algorithm of Jack Ng, [2] and the Wheeler De Witt version of the log of the partition function as presented by Glinka [5] . Doing so may enable researchers to eventually determine if or not gravity/gravitational waves are an emergent field phenomenon.
Let us now examine candidates for entropy and discuss their advantages and limitations.
2.1. Cautions as to What NOT to Do with Entropy-Data Compression-ZPE
In this inquiry, we should take care not to fall into several pit falls of analysis. We should avoid conflating any conceivable connections of zero point energy extraction, especially ZPE, and fluctuation states of ZPE, with data compression. The two do not mix for reasons which will be elaborated upon in the text. Secondly, the discussion we are embarking upon has no connection with intelligent design. Lossless data compression is a class of data compression algorithms that allows the exact original data to be reconstructed from the compressed data. If we are to, as an example, reconstruct information pertinent to keeping the same cosmological parameter values of  from a prior universe to our present, it is important to delineate physical processes allowing for lossless data compression, and to do it in a way which has connections with theologically tainted arguments contaminated with Intelligent Design thinking.
from a prior universe to our present, it is important to delineate physical processes allowing for lossless data compression, and to do it in a way which has connections with theologically tainted arguments contaminated with Intelligent Design thinking.
Alan Heavens et al. [7] identified criteria in an arXIV article stating “We show that, if the noise in the data is independent of the parameters, we can form linear combinations of the data which contain as much information about all the parameters as the entire dataset, in the sense that the Fisher information matrices are identical”, as a criteria for lossless data compression. For our purposes, this is similar to reducing noise in “information transfer” from a prior to a present universe as an ignorable datum which has no bearing upon encoded information values of 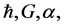 from a prior universe to our present. So how do we make noise as inconsequential?
from a prior universe to our present. So how do we make noise as inconsequential?
We have reviewed A. K. Avessian’s [8] article about alleged time variation of Planck’s constant from the early universe, and found the arguments incomplete, again for reasons which will be discussed later on in the text. What is important would be to specify what would be a minimal amount of information needed to encode/ transmit a value of 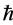 from cosmological cycle to cycle, and to concentrate upon a lossless “data compression” physical process for transmission of that
from cosmological cycle to cycle, and to concentrate upon a lossless “data compression” physical process for transmission of that 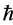 from cosmological cycle to cycle. The main criteria will be to identify a physical process where “noise” in the transmitted data is independent of the value of
from cosmological cycle to cycle. The main criteria will be to identify a physical process where “noise” in the transmitted data is independent of the value of 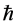 from cosmological cycle to cycle. The preferred venue for such a transmission would be a worm hole bridge from a prior to the present universe, as specified by both Beckwith [9] at STAIF, and. Crowell [10] . Batle-Vallespir cited in his PhD dissertation [11] criteria for the physics of information encoded in very small distances, but we are convinced that something closer to deformation mechanics treatment of quantization criteria will be necessary to tell us how to transmit a value of
from cosmological cycle to cycle. The preferred venue for such a transmission would be a worm hole bridge from a prior to the present universe, as specified by both Beckwith [9] at STAIF, and. Crowell [10] . Batle-Vallespir cited in his PhD dissertation [11] criteria for the physics of information encoded in very small distances, but we are convinced that something closer to deformation mechanics treatment of quantization criteria will be necessary to tell us how to transmit a value of  from cosmological cycle to cycle, via either a worm hole, or similar process, while maintaining lossless “data compression” by making whatever noise would be transmitted as inconsequential to keeping basic parameters intact from cycle to cosmological cycle. The identification of information, as we are doing here, with entropy measurements, makes a through investigation of entropy, and its generation as of high consequence to this inquiry.
from cosmological cycle to cycle, via either a worm hole, or similar process, while maintaining lossless “data compression” by making whatever noise would be transmitted as inconsequential to keeping basic parameters intact from cycle to cosmological cycle. The identification of information, as we are doing here, with entropy measurements, makes a through investigation of entropy, and its generation as of high consequence to this inquiry.
2.2. Minimum Amount of Information Needed to Initiate Placing Values of Fundamental Cosmological Parameters
K. Avessian’s article [8] (2009) about alleged time variation of Planck’s constant from the early universe depends heavily upon initial starting points for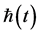 , as given below, where we pick our own values for the time parameters, for reasons we will justify in this manuscript:
, as given below, where we pick our own values for the time parameters, for reasons we will justify in this manuscript:
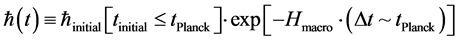 (1)
(1)
The idea is that we are assuming a granular, discrete nature of space time. Furthermore, after a time we will state as t ~ tPlanck there is a transition to a present value of space time, which is then probably going to be held constant.
It is easy to, in this situation, to get an inter relationship of what 



This leads to us asking what can be done to get a starting value of 
We obtain a minimum value as far as “information” via appealing to Hogan’s [12] argument where we have a maximum entropy as

and this can be compared with A. K. Avessian’s article [8] value of, where we pick

I.e. a choice as to how 

ball park estimate as to compressed values of 
universe, to today’s universe. If
Typically though, the value of the Hubble parameter, during inflation itself is HUGE, i.e. H is many times larger than 1, leading to initially very small entropy values. This means that we have to assume, initially, for a minimum transfer of entropy/information from a prior universe, that H is negligible. If we look at Hogan’s holographic model, this is consistent with a non finite event horizon

This is tied in with a temperature as given by

Nearly infinite temperatures are associated with tiny event horizon values, which in turn are linked to huge Hubble parameters of expansion. Whereas initially nearly zero values of temperature can be arguably linked to nearly non existent H values, which in term would be consistent with 

If, in this situation, that N is proportional to entropy, i.e. N as-number of entropy states to consider, then as H drops in size, as would happen in pre inflation conditions, we will have opportunities for N ~ 105
2.3. Is Data Compression a Way to Distinguish What Information Is Transferred to the Present Universe?
The peak temperature as recorded by Weinberg [13] is of the order of 1032 Kelvin, and that would imply using the expansion parameter, H, as given by Equation (5) above. Likely before the onset of inflation, due to dimensional arguments, it can be safe to call the pre inflation temperature, T as very low. I.e. there was a build up of temperature, T, at the instant before inflation, which peaked shortly afterwards. Such an eventuality would be consistent with use of a worm hole bridge from a prior to a present universe. Beckwith [9] used such a model as a transfer of energy to the present universe, using formalism from Crowell’s book [10] . A useful model as far as rapid transfer of energy would likely be a quantum flux, as provided for in Deformation quantization. We will follow the following convention as far as initiating quantization, i.e. the reported idea of Weyl quantization which is as follows: For a classical

Here, C is the inverse Fourier transform, and w (,) is a weight function, and p, and q are canonical variables
fitting into
as refinement of Poisson brackets, the above, Weyl quantization is , as noted by S. Gutt and S. Waldemann [14] (2006) equivalent to finding an operation 

As well as for Poisson brackets, 


For very small regimes of spatial integration, we can approximate Equation (7) as a finite sum, with

What we are doing is to give the following numerical approximate value of, de facto, as follows

the inverse transform is a form of data compression of information. Here, we will state that 


where R refers to a spatial distance from the center of a spherical universe. Appendix II is an accounting of what is known as a pseudo time dependent solution to the Wheeler de Witt equation involving a wormhole bridge between two universes. The metric assumed in Appendix I is a typical maximally symmetric metric, whereas Appendix II is using the Reisssner-Nordstrom metric. We assume, that to first order, if the value of R in


much information from a prior universe, to our own may be addressed, and that the solution 

2.4. Information Bits for 
To begin this inquiry, it is appropriate to note that we are assuming that there is a variation in the value of


[15] article specified a general value of about 
of

Planck’s length, gives us a flux value as to how many gravitons/entropy units are transmitted. The key point is that we wish to determine what is a minimum amount of information bits/attendant entropy values needed for transmission of





For those who doubt that 10−60 grams per rest mass of a graviton can be reconciled with observational tests with respect to the Equivalence Principle and all classical weak-field tests, we refer the readers to Visser’s article about “Mass for the graviton” [16] . The heart of Visser’s calculation for a non zero graviton mass involve placing appropriate small off diagonal terms to the stress tensor T(u, v) calculation
2.5. Limitations of the Quark-Gluon Analogy and How Such Limitations Impact Ads/CFT Correspondence Applications
What is being alluded to, is that variations in the AdS/CFT correspondence applications exist from what is usually assumed for usual matter. The differences, which are due to quark-gluon plasma models breaking down in the beginning of the big bang point to the necessity of using something similar to the counting algorithm as introduced by Ng, as a replacement for typical string theory models in strict accordance to AdS/CFT correspondence.
The goal of exploring the degree of divergence from AdS/CFT correspondence will be in quantifying a time sequence in evolution of the big bang where there is a break from causal continuity.
A break down in causal continuity [4] [17] will, if confirmed, be a way of signifying that encoded information from a prior era has to be passed through to the present universe in likely an emergent field configuration. If much of the information is passed to our present universe in an emergent field configuration, this leaves open the question of if or not there is a time sequence right after the initial phases of the big bang where there was a re constitution of information in traditional four space geometry.
The problem with implying data is compressed, is that this, at least by popular imagination implies highly specific machine/IT analogues. We wish to assure the readers that no such appeal to intelligent design/deity based arguments is implied in this document.
A point where there is a breakage in causal continuity will help determine if or not there is a reason for data compression. In computer science and information theory, data compression or source coding is the process of encoding information using fewer bits (or other information-bearing units) than an unencoded representation would use through use of specific encoding schemes. Using fewer bits of an encoding scheme for “information” may in its own way allow data compression. We need to have a similar model for explaining the degree of information transferred from a prior universe, to the present, while maintaining the structural integrity of the basic cosmological parameters, such as

Again, while avoiding the intelligent design analogies, it is possible to imply that if there was a restriction of information to dimensions other than the typical space time dimensions of four space, with fifth and higher dimensions being our information conduit, that by default, data compression did occur during the restriction of much of the information encoded in kink-anti kink gravitons disappearing before the big bang in four space, and then re appearing in our present day four space geometry, as a spill over from a fifth dimension.
Since there is a problem physicists, writers, and editors have with any remote degree of ambiguity, let us briefly review what is known about singularity theorems for GR, in four space. Then make a reasonable extrapolation in fifth space embedding of the four dimensions, to make our point about singularities in four space more understandable.
Feinstein, et al. [18] laid out how singularities can be removed from the higher-dimensional model when only one of the extra dimensions is time-varying. If the fifth dimension has, indeed time variance, in any number of ways, four dimensional singularities no longer have the same impact with a time dependent fifth dimensions. And a varying fifth higher dimension is, in itself, a perfect conduit for information from a prior universe, to our present universe. The information restriction in four dimensions, then in four dimensions is a causal discontinuity, while the fifth dimension, with its time variance will be, due to information restriction from four dimensions, our avenue for data “compression” of transferal of information from a prior universe to our present. Furthermore, the spill over from a restriction in four space, to five spaces, with the dumping of information/entropy in present four space after it transfers from a prior universe corresponds to graviton re combination from kink-anti kink structures as entropy increases from a very low level.
This will be done, especially when entropy is held to be in tandem with a “particle count” of instanton-anti instanton packaged gravitons as the mechanism for increase of entropy from a much lower level to today’s level. To begin this analysis, let us look at what goes wrong in models of the early universe. The assertion made is that this is due to the quark-Gluon model of plasmas having major “counting algorithm” breaks with non counting algorithm conditions, i.e. when plasma physics conditions BEFORE the advent of the Quark gluon plasma existed. Here are some questions which need to be asked [19] - [22] .
1. Is QGP strongly coupled or not? Note: Strong coupling is a natural explanation for the small (viscosity).
Analogy to the RHIC: J/y survives deconfinement phase transition.
2. What is the nature of viscosity in the early universe? What is the standard story? (Hint: AdS-CFT correspondence models). Question 2 comes up since [23] .

Typically holds for liquid helium and most bosonic matter. However, this relation breaks down. At the beginning of the big bang. As follows.
I.e. if Gauss-Bonnet gravity is assumed, in order to still keep causality, one needs to have Equation (11) satisfied.
This even if one writes for a viscosity over entropy ratio the following [20] - [23] , so if 

A careful researcher may ask why this is so important. If a causal discontinuity as indicated means the
ratio is

collisions due to WHAT physical process? Recall the argument put up earlier. I.e. the reference to causal discontinuity in four dimensions, and a restriction of information flow to a fifth dimension at the onset of the big bang/transition from a prior universe? That process of a collision increase may be inherent in the restriction to a fifth dimension, just before the big bang singularity, in four dimensions, of information flow. In fact, it very well be true, that initially, during the process of restriction to a 5th dimension, right before the big bang, that

in geometric “sizing” may become effectively nearly infinite.
It is due to the following qualifications put in about Quark-Gluon plasmas which will be put up, here. Namely, more collisions imply less viscosity. More Deflections ALSO implies less viscosity. Finally, the more momentum transport is prevented, the less the viscosity value becomes. Say that a physics researcher is looking at viscosity due to turbulent fields. Also, perturbatively calculated viscosities: due to collisions. This has been known as Anomalous Viscosity in plasma physics, [21] (this is going nowhere, from pre-big bang to big bang cosmology).
So happens that RHIC models for viscosity assume [20] - [23] .

As Akazawa [21] noted in an RHIC study, Equation (13) above makes sense if one has stable temperature T, so that

If the temperature T wildly varies, as it does at the onset of the big bang, this breaks down completely. This development is Mission impossible: why we need a different argument for entropy. I.e. Even for the RHIC, and in computational models of the viscosity for closed geometries-what goes wrong in computational models
• Viscous Stress is NOT µ shear
• Nonlinear response: impossible to obtain on lattice ( computationally speaking)
• Bottom line: we DO NOT have a way to even define SHEAR in the vicinity of big bang!!!!
We now need to ask ourselves what may be a way to present entropy/entropy density in a manner which may
be consistent with having/explaining how 
how the entropy/entropy density may become extraordinarily large, and that, outside of the restriction to a fifth dimension argument mentioned earlier for “information” transferal to the onset of the big bang, that it is not necessary to appeal to nearly infinite collisions in order to have a drop in viscosity. This will lead to Ng’s “particle count” algorithm [2] for entropy, below
2.6. Is Each “Particle Count Unit” as Brought Up by Ng, Is Equivalent to a “Brane-Anti Brane” Unit in Brane Treatments of Entropy?
It is useful to state this convention for analyzing the resulting entropy calculations, because it is a way to explain how and why the number of instanton-anti instanton pairs, and their formulation and break up can be linked to the growth of entropy. If, as an example, there is a linkage between quantum energy level components of the quantum gas as brought up by Glinka [5] (2007) and the number of instanton-anti instanton pairs, then it is possible to ascertain a linkage between a Wheeler De Witt worm hole introduction of vacuum energy from a prior universe to our present universe, and the resulting brane-anti brane (instanton-anti instanton) units of entropy. What would be ideal would be to make an equivalence between a quantum number, n, say of a quantum graviton gas, as entering a worm hole, i.e. going back to the Energy (quantum gas)


Furthermore, finding out if or not it is either a drop in viscosity, when
entropy density may tell us how much information is, indeed, transferred from a prior universe to our present. If it is

This leaves open the question of if or not there is “infinite” density of ordinary matter, or if or not there is a fifth dimensional leakage of “information” from a prior universe to our present. If there is merely infinite “density”, and possibly infinite entropy “density/disorder at the origin, then perhaps no information from a prior universe is transferred to our present universe. On the other hand, having


Details about this have to be worked out, and this because that as of present one of the few tools which is left to formulation and proof of the singularity theorems is the Raychaudhuri equation, which describes the divergence θ of a congruence (family) of geodesics, which has a lot of assumptions behind it, as stated by Dadhich [23] . As indicated by Hawking’s theorem, infinite density is its usual modus operandi, for a singularity, and this assumption may have to be revisited. Natário [24] has more details on the different type of singularities involved.
2.7. Ng’s Particle Count Algorithm and Brane Models of Entropy
Let us first summarize what can be said about Ng’s quantum infinite statistics. Afterwards, the numerical counting involved has a direct connection with the pairs of brane-anti brane (kink-anti kink) structures Mathur and others worked with to get an entropy count. Ng [1] outlines how to get



This, according to Ng, leads to entropy of the limiting value of

But

The supposition is that the value of N is proportional to a numerical DM density referred to as
HFGW would play a role if 

linkage made between 


Such a linkage would open up the possibility that the density of primordial gravitational waves could be examined, and linked to modeling gravity as an effective theory, as well as giving credence to how to avoid dS/dt = ∞ at S = 0. If so, then one can look at the research results of Samir Mathur [26] (2007). This is part of what has been developed in the case of massless radiation, where for D space-time dimensions, and E, the general energy is

This suggests that entropy scaling is proportional to a power of the vacuum energy, i.e., entropy ~ vacuum energy, if 

Traditionally, minimum length for space-time benchmarking has been via the quantum gravity modification of a minimum Planck length for a grid of space-time of Planck length, whereas this grid is changed to something
bigger
entropy. 






This expression for entropy (based on the number of brane-anti-brane pairs) has a net energy value of 



Equation (22) can be changed and rescaled to treating the mass and the energy of the brane contribution along the lines of Mathur’s CQG [26] article (2007) where he has a string winding interpretation of energy: putting as much energy E into string windings as possible via








The windings of a string are given by figure 6.1 of Becker et al [32] , as the number of times the strings wrap about a circle midway in the length of a cylinder. The structure the string wraps about is a compact object construct Dp branes and anti-branes. Compactness is used to roughly represent early universe conditions, and the brane-anti brane pairs are equivalent to a bit of “information” This leads to entropy expressed as a strict numerical count of different pairs of Dp brane-Dp anti-branes, which form a higher-dimensional equivalent to graviton production. The tie in between Equation (24) below and Ng’s [1] treatment of the growth of entropy is as follows: First, look at the expression below, which has 


2.8. Ng’s Particle Count Algorithm and Brane Models of Entropy
We start off with looking at Vacuum energy and entropy. This suggests that entropy scaling is proportional to a power of the vacuum energy, i.e., entropy ~ vacuum energy, if is interpreted as a total net energy proportional to vacuum energy, i.e. go to Equation (10) above. What will be done is hopefully, with proper analysis of T(u, v) at the onset of creation, is to distinguish, between entropy say of what Mathur [26] wrote, as

This needs to be compared with the entropy of the universe, as given by Sean Carroll, as stated by [5]

The claim made here is that if one knew how to evaluate T(u, v) properly, that the up to 109 difference in Equations (25) and (26) will be understandable, and that what seems to be dealt with directly. Doing so is doable if one understands the difference/similarities in Equations (21), (23), and (24), above. So, how does one do this? The candidate picked which may be able to obtain some commonality in the different entropy formalisms is to confront what is both right and wrong in Seth Lloyd’s entropy treatment in terms of operations as given below. Furthermore, what is done should avoid the catastrophe inherent in solving the problem of dS/dt = ∞ at S = 0 as stated to the author in a presentation he saw [33] [34] in Kochi, India, as a fault of classical GR which should be avoided. One of the main ways to perhaps solve this will be to pay attention to what Unnikrishnan [35] put up in 2009 at ISEG, Kochi, India, i.e. his article about the purported one way speed of light, and its impact upon perhaps a restatement of T(u, v). A re statement of how to evaluate T(u, v) may permit a proper frame of reference to close the gap between entropy values as given in Equations (25) and Equations (26) above.
2.9. Seth Lloyd’s Linking of Information to Entropy
By necessity, entropy will be examined, using the equivalence between number of operations which Seth Lloyd used in his model, and total units of entropy as the author referenced from Carroll, and other theorists. The key equation Lloyd [2] wrote is, assuming a low entropy value in the beginning

Lloyd is making a direct reference to a linkage between the number of operations a quantum computer model of how the Universe evolves is responsible for, in the onset of a big bang picture, and entropy. If Equation (27) is accepted then the issue is what is the unit of operation, i.e. the mechanism involved for an operation for assembling a graviton, and can that be reconciled with T(0, 0) as could be read from Equation (28) below.
2.10. Simple Relationships to Consider (with Regards to Equivalence Relationships Used to Evaluate T(u, v))
What needs to be understood and evaluated is, if there is a re structuring of an appropriate frame of reference for T(u, v) and its resultant effects upon how to reconcile black hole entropy, a.k.a. Equation (25) with Equation (26) and Equation (27). A good place to start would be to obtain T(u, v) values which are consistent with slides on the two way versus one way light speed presentation of the ISEG 2009 conference. We wish to obtain T(u, v) values properly analyzed with respect to early universe metrics, and PROPERLY extrapolated to today so that ZPE energy extraction, as pursued by many, will be the model for an emergent field development of entropy. Note the easiest version of T(u, v) as presented by [36] Wald. If metric g(a, b) is for curved space time, the simplest matter energy stress tensor is (Klein Gordon)

What is affected by Unnikrishnan’s presented (2009) [35] hypothesis is how to keep g(a, b) properly linked observationally to a Machian universe frame of reference, not the discredited aether, via CMBR spectra behavior. If the above equation is held to be appropriate, and then elaborated upon, the developed T(u, v) expression should adhere to Wald’s unitary equivalence principle. The structure of unitary equivalence is foundational to space time maps, and Wald states it as being

While stating this, it is important to keep in mind that Wald defines [36]

We defined the operation, where A is a bounded operator, and < > an inner product via use of [36]

The job will be to keep this same equivalence relationship intact for space time, no matter what is done with the metric g(a, b) in the T(a, b) expressions we work with, which will be elaborations of Equation (28) above.
3. Experimental Section Collection, Namely Data Analysis via Graviton Production Conflated with Entropy
This is closely tied in with data compression and how much “information” material from a prior universe is transferred to our present universe. In order to do such an analysis of data compression and what is sent to out present universe from a prior universe, it is useful to consider how there would be an eventual increase in information/entropy terms, from 1021 to 1088. Too much rapid increase would lead to the same problem ZPE researchers have. I.e. if Entropy is maximized too quickly, we have no chance of extracting ZPE energy from a vacuum state, i.e. no emergent phenomena is possible. What to avoid is akin to [37] avoiding

Equation (32) is from Giovanni, and it states that all entropy in the universe is solely due to graviton production [37] . This absurd conclusion would be akin, in present day parlance, to having 1088 entropy “units” created right at the onset of the big bang. This does NOT happen.
What will eventually need to be explained will be if or not 107 entropy units, as information transferred from a prior big bang to our present universe would be enough to preserve 

do so, that Equation (27), and a mechanism for the assembly of gravitons from a kink-anti kink structure is a de rigor development. We need to find a way to experimentally verify this tally of results. And to find conditions under which the abrupt reformulation of a near-constant cosmological constant, i.e., more stable vacuum energy conditions right after the big bang itself, would allow for reformulation of SO (4) gauge-theory conditions.
What Is the Bridge between Low Entropy of the Early Universe and Its Rapid Build up Later
Penrose in a contribution to a conference, [38] [39] on page two of the Penrose document refers to reconciling a tiny initial starting entropy of the beginnings of the universe with a much larger increased value of entropy substantially later. As from the article by Penrose [39] “A seeming paradox arises from the fact that our best evidence for the existence of the big bang arises from observations of the microwave background radiation-“…..” This (statement) corresponds to maximum entropy so we reasonably ask: how can this be consistent with the Second law, according to which the universe started with a tiny amount of entropy”. Penrose then goes on to state that “The answer lies in the fact that the high entropy of the microwave background only refers to the matter content of the universe, and not the gravitational field, as would be enclosed by its space-time background in accordance to Einstein’s theory of general relativity”. Penrose then goes on to state that the initial pre red shift equals 1100 background would be remarkably homogeneous. I.e. for red shift values far greater than 1100 the more homogeneous the universe would become according to the dictum that “gravitational degrees of freedom would not be excited at all” Beckwith [40] then asks the question of how much of a contribution the baryonic matter contribution would be expected to make to entropy production. The question should be asked in terms of the time line as to how the universe evolved, as specified by both Steinhardt and Turok [41] on pages 20 - 21 of their book, as well as by NASA. And a way to start this would be to delineate further the amplitude vs frequency GW plot as given below. It is asserted that the presence of the peak in gravity wave frequency at about 1010 Hertz (shown in Figure 1) has significant consequences for observational cosmology as seen in [42] .
We are attempting to find an appropriate phase transition argument for the onset of entropy creation and the right graviton production expression needed [43]

Is akin to explaining how, and why temperature changes in T, lead to, if the temperature increases, an emergent
Figure 1. Where HFGWs come from: Grishchuk found the maximum energy density (at a peak frequency) of relic gravitational waves (Grishchuk, 2007) [42] .
field description of how gravitons arose. We claim that this is identical to obtaining a physically consistent description of entropy density would be akin to, with increasing, then decreasing temperatures a study as to how kink-anti kink structure of gravitons developed. This would entail developing a consistent picture, via SO (4) theory of gravitons being assembled from a vacuum energy back ground and giving definition as to Seth Lloyd’s computation operation [2] description of entropy. Having said this, it is now appropriate to raise what gravitons/ HFGW may tell us about structural evolution issues in today’s cosmology. Here are several issues the author is aware of which may be answered by judicious inquiry. As summarized by Padmanabhan [44] (IUCAA) in the recent 25th IAGRG presentation he made, “Gravity: The Inside Story”, entropy can be thought of as due to “ignored” degrees of freedom, classically, and is generalized in general relativity by appealing to extremising entropy for all the null surfaces of space time. Padmanabhan claims the process of extemizing entropy then leads to equations for the background metric of the space-time. I.e. that the process of entropy being put in an extremal form leads to the Einsteinian equations of motion. What is done in this present work is more modest. I.e. entropy is thought of in terms of being increased by relic graviton production, and the discussion then examines the consequence of doing that in terms of GR space time metric evolution. How entropy production is tied in with graviton production is via recent work by Jack Ng. It would be exciting if or not we learn enough about entropy to determine if or not we can identify null surfaces, as Padamanadan brought up in his presentation in his Calcutta [44] (2009) presentation. The venue of research brought up here we think is a step in just that direction. Furthermore, let us now look at large scale structural issues which may necessitate use of HFGW to resolve. Job one will be to explain what may the origins of the enormous energy spike in Figure 1 above, by paying attention to Relic gravitational waves, allowing us to make direct inferences about the early universe Hubble parameter and scale factor (“birth” of the Universe and its early dynamical evolution). According to Grishchuk [42] : Energy density requires that the GW frequency be on the order of (10 GHz), with a sensitivity required for that frequency on the order of 10−30 δm/m. Once this is obtained, the evolution of cosmological structure can be investigated properly, with the following as targets of opportunity for smart applications of HFGW detectors.
4. Conclusions
Let us first reference what can be done with further developments in deformation quantization and its applications to gravitational physics. The most noteworthy the author has seen centers upon Grassman algebras and deformation quantization of fermionic fields. We note that Galaviz [45] showed that one can obtain a Dirac propagator from classical versions of Fermionic fields, and this was a way to obtain minimum quantization conditions for initially classical versions of fermionic fields due to alterations of algebraic structures, in suitable ways. One of the aspects of early universe topology we need to consider is how to introduce quantization in curved space time geometries,
and this is a problem which would, among other things permit a curved space treatment of
should be aware that as spatial variable R gets to be the order of
field theory quantization condition for
path integrals. We claim that deformation quantization, if applied successfully willeventually lead to a great refinement of the above Wheeler De Witt wave functional value, as well as allow a more through match up of a time independent solution of the Wheeler De Witt equation, as given in Appendix I. We claim that the linkage between time independent treatments of the wave functional of the universe, with what Lawrence Crowell [9] wrote up in 2005, will be made more explicit. This will, in addition allow us to understand better how graviton production in relic conditions may add to entropy, as well as how to link the number of gravitons, say 1012 gravitons per photon, as information as a way to preserve the continuity of 

tons/information can pass through minimum vales of

This expression of power should be compared with the one presented by Giovannini [38] on averaging of the energy-momentum pseudo tensor to get his version of a gravitational power energy density expression, namely

It is important to note that Giovannini [38] states that should the mass scale be picked such that


different procedures to come up with relic gravitational wave detection schemes to get quantifiable experimental measurements so we can start predicting relic gravitational waves. This is especially true if we make use of the following formula for gravitational radiation, as given by Koffman [48] , with 

We will be trying to get to the bottom of what was listed, especially in the DM/DE conundrums, probably by judicious application of good high frequency detector work.
If we obtain good data, via appropriate work, we intend to, confirm via measurements the following Figure 2. This also means paying attention to [48] . In addition, we should do data analysis so what is measured by Equa-
Figure 2. The amplitude and frequency of the HFGWs expected by the brane oscillation models in the submillimeter-size extra dimensions. The figure is taken from Clarkson, C. [52] and Seahra, S.S, where l is the curvature scalar of the bulk, d is the distance between the “visible” brane and the “shadow” brane.
tion (36) is not affected by the Graceful exit (from inflation) as mentioned in [49] .
Note that this research development should include the research results by Dr. Corda as of [50] . We wish to delineate between General relativity and scalar-tensor theories of gravity experimentally. Either theory as given by [50] is applicable in the Planckian space-time regime for formation of foundations of gravity. This also touches upon issues brought up in [51] [52] .
Furthermore we should note that the development of confirmation of Figure 2 is the main reason for the research work in High Frequency Gravitational waves, initiated by Chongqing University. I.e. it is important that the details of pre heating after inflation, as given in [50] also be accounted for, as that would influence then how we would measure the HFGW of Figure 2 above, i.e. the main issue be the stochastic noise background cannot be too noisy for us to measure these waves effective. Not to mention also that the issue brought up by Dr. Corda, in [50] must be clarified, i.e. are we seeing a scalar-tensor background to gravity which would mean a different genesis of Gravity itself than Relativity? Or do we still adhere to the brane oscillation model as closely linked to GR? i.e. this has to be settled. And hopefully will be in the coming decade. Not to mention [51] which is that we have to not contravene the recent LIGO discovery in our present examination metrics. And of course the details of Clarkson, in [52] cannot be ignored.
Acknowledgements
The author wishes to thank Dr. Fangyu Li as well as Stuart Allen, of international media associates whom freed the author to think about physics, and get back to his work. This work is supported in part by National Nature Science Foundation of China grant No. 110752.
Cite this paper
Andrew W. Beckwith, (2016) Relic Entropy Growth and Initial Big Bang Conditions, as a Subset of Quantum Information. Journal of High Energy Physics, Gravitation and Cosmology,02,392-411. doi: 10.4236/jhepgc.2016.23035
References
- 1. Visser, M. (1998) Mass for the Graviton. General Relativity and Gravitation, 30, 1717-1728. http://arxiv.org/abs/gr-qc/9705051 http://dx.doi.org/10.1023/A:1026611026766
- 2. Beckwith, A., Li, F.Y., Yang, N., Dickau, J., Stephenson G., Glinka, L. (2011) Is Octonionic Quantum Gravity Relevant near the Planck Scale? If Gravity Waves Are Generated by Changes in the Geometry of the Early Universe, How Can We Measure Them? A Chapter in Cosmology Book, Nova Book Publishersn. http://vixra.org/abs/1101.0017
- 3. Feinstein, A. and Vazquez-Mozo, M.A. (2000) M-Theory Resolution of Four-Dimensional Cosmological Singularities via U-Duality. Nuclear Physics B, 568, 405-420.
http://arxiv.org/abs/hep-th/9906006/
http://dx.doi.org/10.1016/S0550-3213(99)00697-5 - 4. Nonakaa, C. and Bass S.A. (2006) 3-D Hydro + Cascade Model at RHIC. Nuclear Physics A, 774, 873-876. http://dx.doi.org/10.1016/j.nuclphysa.2006.06.155
- 5. Asakawa, M., Bass, S.A. and Müller, B. (2006) Anomalous Viscosity of an Expanding Quark-Gluon Plasma. Physical Review Letters, 96, 252301. http://dx.doi.org/10.1103/PhysRevLett.96.252301
- 6. Asakawa, M., Hatsuda, T. and. Nakahara, Y. (2001) Maximum Entropy Analysis of the Spectral Functions in Lattice QCD. Progress in Particle and Nuclear Physics, 46, 459-508.
http://dx.doi.org/10.1016/S0146-6410(01)00150-8 - 7. Torrieri, G. and Mishustin, I. (2008) Instability of Boost-Invariant Hydrodynamics with a QCD Inspired Bulk Viscosity. Physical Review C, 78, 021901.
http://arxiv.org/abs/0805.0442
http://dx.doi.org/10.1103/physrevc.78.021901 - 8. Son, D.T. AdS/CFT and Viscosity Bound. http://npl09.phy.duke.edu/talks/Son_NPFW.pdf
- 9. Dadhich, N. (2005) Derivation of the Raychaudhuri Equation. http://arxiv.org/abs/gr-qc/0511123
- 10. Natário, J. (2006). Relativity and Singularities—A Short Introduction for Mathematicians.
http://arxiv.org/abs/math.DG/0603190 - 11. Beckwith, A.W. (2009) Relic High Frequency Gravitational Waves from the Big Bang, and How to Detect Them. AIP Conference Proceedings, 1103, 571-581. (SPESIF)
http://arxiv.org/abs/0809.1454
http://dx.doi.org/10.1063/1.3115567 - 12. Mathur, S. and Chowdhury, B. (2007) Fractional Brane States in the Early Universe. Classical and Quantum Gravity, 24, 2689-2720. http://dx.doi.org/10.1088/0264-9381/24/10/014
- 13. Beckwith, A.W. (2007) Presented at 6th International Conference on Gravitation and Cosmology (ICGC 2007). Pune, 17-21 December 2007, in 20 Minute Presentation.
- 14. Beckwith, A.W. (2008) Penrose Model Potential, Compared with Coleman-Weinberg Potential for Early Universe Scalar Evolution. Electronic Journal of Theoretical Physics, 5N17, 95-106.
- 15. Lifschytz, G. (2004) Black Hole Thermalization Rate from Brane Antibrane Model. Journal of High Energy Physics, 08, 059. http://dx.doi.org/10.1088/1126-6708/2004/08/059
- 16. Beckwith, A.W. (2006) A New Soliton-Anti Soliton Pair Creation Rate Expression Improving upon Zener Curve Fitting for I-E Plots. Modern Physics Letters B, 20, 849-861.
http://arxiv.org/abs/math-ph/0411045
http://dx.doi.org/10.1142/S0217984906011219 - 17. Beckwith, A.W. (2001) Classical and Quantum Models of Density Wave Transport: A Comparative Study. PhD Dissertation, University of Houston Physics Department, Houston.
- 18. Becker, M., Leblond, M. and Shandera, S. (2007) Inflation from Wrapped Branes. Physical Review D, 76, 12351.
http://prd.aps.org/abstract/PRD/v76/i12/e123516
http://dx.doi.org/10.1103/physrevd.76.123516 - 19. Mithras, A. (2009) Personal Communications Exchanged with Author at ISEG 2009, in Kochi, India.
- 20. Mithra, A (2011) Why No Dark Energy, No Big Bang, But a Likely Fractal Universe? Presented at 32nd International Cosmic Ray Conference, Beijing 2011, Volume 5, 219-222.
http://galprop.stanford.edu/elibrary/icrc/2011/papers/HE3.5/icrc0794.pdf - 21. Unnikrishnan, C.S. The One Way Speed of Light and Implications for Relativity Theories.
http://www.space-lab.ru/files/pages/PIRT_VII-XII/pages/text/PIRT_X/Unnikrishnan_1.pdf - 22. Wald, R.M. (1994) Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics (Chicago Lectures in Physics). University Of Chicago Press, Chicago, Illinois, USA.
- 23. Giovannini, M. (2008) A Primer on the Physics of the Cosmic Microwave Background. World Press Scientific, Singapore, Republic of Singapore. http://dx.doi.org/10.1142/6730
- 24. Penrose, R. (2010) Cycles of Time: An Extraordinary New View of the Universe. The Bodley Head, London, UK.
- 25. Penrose, R. (2006) Before the Big Bang: An Outrageous New Perspective and Its Implications for Particle Physics. Proceedings of EPAC, Edinburgh, Scotland, 2759-2763.
- 26. Steinhardt, P.J. and Turok, N. (2007) Endless Universe, Beyond the Big Bang. Doubleday Broadway Publishing Group, a Division of Random House Inc., New York.
http://map.gsfc.nasa.gov/media/060915/index.html - 27. Grishchuk, L. (2008) Discovering Relic Gravitational Waves in Cosmic Microwave Background Radiation. http://arxiv.org/abs/0707.3319
- 28. Kolb, E. and Turner, S. (1994) The Early Universe. Westview Press, Chicago.
- 29. Thanu, P. (2008) From Gravitons to Gravity: Myths and Reality. International Journal of Modern Physics D, 17, 367- 398. http://dx.doi.org/10.1142/S0218271808012085
- 30. Galvaviz, I. (2007) Deformation Quantization for Fermionic Fields. Reviews Mexicana De Fisica S, 53, 51-55
- 31. Fontana, G. (2005) Gravitational Wave Propulsion. In: El-Genk, M.S., Ed., CP746, Space Technology and Applications International Forum-STAIF 2005, American Institute of Physics, Melville.
- 32. Park, D. (1955) Radiations from a Spinning Rod. Physical Review, 99, 1324-1325.
http://dx.doi.org/10.1103/PhysRev.99.1324 - 33. Honig, W.M. (1974) A Minimum Photon Rest Mass-Using Planck’s Constant and Discontinuous Electromagnetic Waves. Foundations of Physics, 4, 367-380. http://dx.doi.org/10.1007/BF00708542
- 34. Gutt, S. and Waldmann, S. (2006) Deformation of the Poisson Bracket on a Sympletic Manifold. In: Franciose, Naber, and Tsun, Eds., The Encyclopedia of Mathematical Physics; Algebraic Topology; Sympletic Geometry and Topology; Ordinary and Partial Differential Equations, Volume 11, 119-129.
- 35. Weinberg, S. (1973) Gravitation. Freeman, San Francisco.
- 36. Hogan, C. (2002) Holographic Discreteness of Inflationary Perturbations. Physical Review D, 66, Article ID: 023521. arXiv:astro-ph/0201020v2. http://dx.doi.org/10.1103/PhysRevD.66.023521
- 37. Batle-Vallespir, J. (2006) Characterization of Quantum Entangled States and Information Measures. Ph.D. Dissertation. http://cdsweb.cern.ch/record/935088/files/0603124.pdf
- 38. Crowell, L. (2005) Quantum Fluctuations of Space Time. World Scientific Series in Contemporary Chemical Physics, 25, World Scientific, PTE, LTD, Singapore.
- 39. Beckwith, A.W. (2008) Implications for the Cosmological Landscape: Can Thermal Inputs from a Prior Universe Account for Relic Graviton Production? AIP Conference Proceedings, 969, 1091-1102.
http://dx.doi.org/10.1063/1.2844947
https://arxiv.org/abs/0803.0101 - 40. Avetissian, A.K. (2009) Plancks Constant Evolution as a Cosmological Evolution Test for the Early Universe. Gravitation and Cosmology, 15, 10-12. http://dx.doi.org/10.1134/S0202289309010034
- 41. Heavens, A., Jimenez, R. and Lahav, O. (2000) Massive Lossless Data Compression and Multiple Parameter Estimation from Galaxy Spectra. Monthly Notices of the Royal Astronomical Society, 317, 965. http://arxiv.com/abs/astro-ph/9911102 http://dx.doi.org/10.1046/j.1365-8711.2000.03692.x
- 42. Carroll, S. (2004) An Introduction to General Relativity Space Time and Geometry. Addison Wesley Publishing House, San Francisco.
- 43. Glinka, L. (2007) Quantum Information from Graviton-Matter Gas. Sigma, 3, 087, 13 p. https://www.emis.de/journals/SIGMA/2007/087/sigma07-087.pdf
- 44. Dowker, H.F. (2005) Causal Sets and the Deep Structure of Spacetime. In: Ashtekar, A., Ed., 100 Years of Relativity Space-Time Structure: Einstein and Beyond, World Press Scientific, Singapore, 445-464. arXIV gr-qc/0508109v1
- 45. Lloyd, S. (2002) Computational Capacity of the Universe. Physical Review Letters, 88, 237901
http://dx.doi.org/10.1103/PhysRevLett.88.237901 - 46. Ng, Y.J. (2008) Space-Time Foam: From Entropy and Holography to Infinite Statistics and Nonlocality. Entropy, 10, 441-461.
- 47. Ramallo, A. (2013) Introduction to the AdS/CFT Correspondence. http://arxiv.org/abs/1310.4319
- 48. Koffman, L. (2008) Pre Heating after Inflation. In: Lemoine, M., Martin, J. and Peter, P., Eds., Lecture notes in Physics 738, Springer Verlag, Berlin, 55-79. http://dx.doi.org/10.1007/978-3-540-74353-8_2
- 49. Kawai, S. and Soda, J. (1999) Evolution of Fluctuations during Graceful Exit in String Cosmology. Physics Letters B, 460, 41-46. http://dx.doi.org/10.1016/S0370-2693(99)00736-4
- 50. Corda, C. (2009) Interferometric Detection of Gravitational Waves: The Definitive Test for General Relativity. International Journal of Modern Physics D, 18, 2275-2282. http://arxiv.org/abs/0905.2502 http://dx.doi.org/10.1142/S0218271809015904
- 51. Abbott, B.P., et al., LIGO Scientific Collaboration and Virgo Collaboration (2016) Observation of Gravitational Waves from a Binary Black Hole Merger. Physical Review Letters, 116, Article ID: 061102. https://physics.aps.org/featured-article-pdf/10.1103/PhysRevLett.116.061102
- 52. Clarkson, C., Clarkson, C. and Seahra, S.S. (2007) A Gravitational Wave Window on Extra Dimensions. Classical and Quantum Gravity, 24, F33. http://dx.doi.org/10.1088/0264-9381/24/9/f01
- 53. Capozziello, S., Feoli, A., Lambiase, G. and Papini, G. (2000) Thin Shell Quantization in Weyl Space-Time. Physics Letters A, 273, 25-30.
Appendix 1: Linking the Thin Shell Approximation, Weyl Quantization, and the Wheeler De Witt Equation
This is a re capitulation of what is written by S. Capoziello, [53] et al. (2000) for physical review A, which is assuming a generally spherically symmetric line element. The upshot is that we obtain a dynamical evolution equation, similar in part to the Wheeler De Witt equation which can be quantified as 


so that 

Similarly, 

Also, when

Realistically, in terms of applications, we will be considering very small x values, consistent with conditions near a singularity/wormhole bridge between a prior to our present universe. This is for
Appendix II. How to Obtain Worm Hole Bridge between Two Universes, via the Wheeler de Witt Equation
We are using reference [9] as a way to use worm hole physics directly. By forming Crowell’s Time Dependent Wheeler-de-Witt Equation, And using its Links to Wormholes This will be to show some things about the wormhole we assert the instanton traverses en route to our present universe. This is the Wheeler-De-Witt equation with pseudo time component added. From Crowell [9]

This has when we do it


In order to do this, we can write out the following for the solutions to Equation (1) above.

And

This is where 



so happens that this is for forming the wave functional that permits an instanton to form. Next, we should consider whether or not the instanton so formed is stable under evolution of space-time leading up to inflation. To model this, we use results from Crowell (2005) on quantum fluctuations in space-time, which gives a model from a pseudo time component version of the Wheeler-De-Witt equation, with use of the Reinssner-Nordstrom metric to help us obtain a solution that passes through a thin shell separating two space-times. The radius of the shell 


This has:

This assumes that the cosmological vacuum energy parameter has a temperature dependence as outlined by Park (2003), leading to

as a wave functional solution to a Wheeler-De-Witt equation bridging two space-times. This solution is similar to that being made between these two space-times with “instantaneous” transfer of thermal heat, as given by Crowell (2005)

This has 

Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/










