Advances in Pure Mathematics
Vol.2 No.5(2012), Article ID:22809,5 pages DOI:10.4236/apm.2012.25052
Global Attractor for a Non-Autonomous Beam Equation*
1Department of Mathematic, Taiyuan University of Technology, Taiyuan, China
2CSIRO Sustainable Ecosystems, Highett, Australia
Email: renyonghua@tyut.edu.cn, #jianwen.z2008@163.com
Received April 10, 2012; revised May 13, 2012; accepted May 21, 2012
Keywords: global attractor; non-autonomous beam equation; absorbing set
ABSTRACT
This work studies the global attractor for the process generated by a non-autonomous beam equation 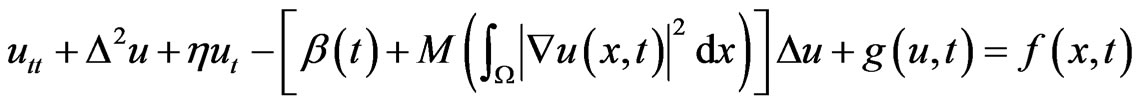 Based on a time-uniform priori estimate method, we first in the space
Based on a time-uniform priori estimate method, we first in the space 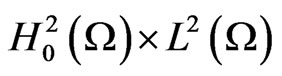 establish a time-uniform priori estimate of the solution
establish a time-uniform priori estimate of the solution  to the equation, and conclude the existence of bounded absorbing set. When the external term
to the equation, and conclude the existence of bounded absorbing set. When the external term  is time-periodic, the continuous semigroup of solution is proved to possess a global attractor.
is time-periodic, the continuous semigroup of solution is proved to possess a global attractor.
1. Introduction
Let  be an open bounded connected domain in
be an open bounded connected domain in 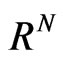 with smooth boundary
with smooth boundary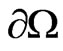 . In this work, we are devoted to the investigation of the following problem for a perturbed non-autonomous beam equation
. In this work, we are devoted to the investigation of the following problem for a perturbed non-autonomous beam equation
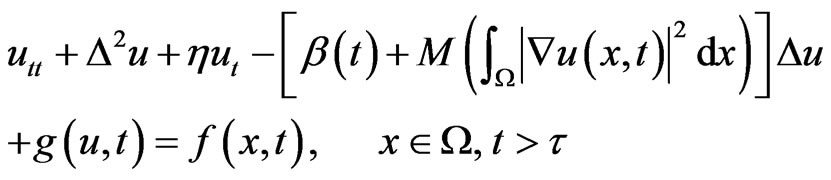 (1)
(1)
with the following initial and boundary conditions
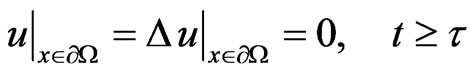 (2)
(2)
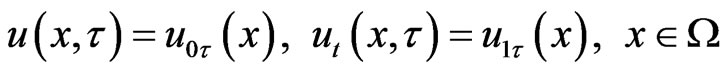 (3)
(3)
where 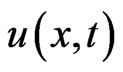 denotes a real-valued unknown function, and describes the transversal motion of the non-autonomous beam.
denotes a real-valued unknown function, and describes the transversal motion of the non-autonomous beam. 
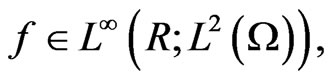
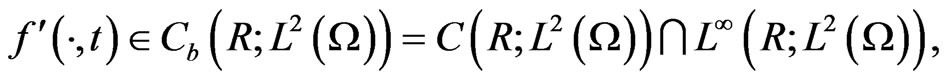
and 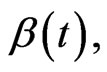
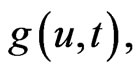
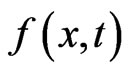 is the time-periodic external force.
is the time-periodic external force.
System (1)-(3) is derived from the vibrations of an non-autonomous beam equation, and its dynamical setting is presented by Woinowsky-Krieger [1] as the new idea in fields of J. Appl. Mech. For the non-autonomous wave equations, there are many interesting results were published focusing different respects (see [2,3]). The focus of this work is the study of the long-term properties of the dynamical system generated by global attractor, please refer the reader to [4,5] and references therein.
This paper is organized as follows. In Section 2, we introduce the main assumptions and discuss the existence of a family of solution operators 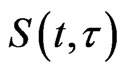 to the problem (1)-(3). Section 3 is devoted to the existence of the bounded absorbing set. In Section 4, we show the continuity of the semigroup operator. Finally, in Section 5, the global attractor is obtained.
to the problem (1)-(3). Section 3 is devoted to the existence of the bounded absorbing set. In Section 4, we show the continuity of the semigroup operator. Finally, in Section 5, the global attractor is obtained.
2. Assumptions and the Existence of the Solution Operators S(t, τ)
Firstly, we assume that the nonlinear functions  satisfied the following conditions. Namely, there exist two constants
satisfied the following conditions. Namely, there exist two constants  such that
such that
(H1)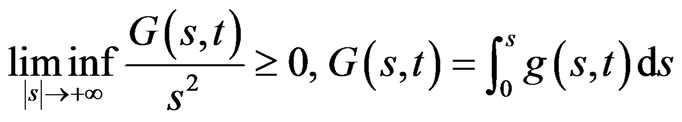 (4)
(4)
(H2)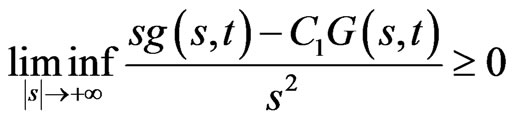 (5)
(5)
(H3)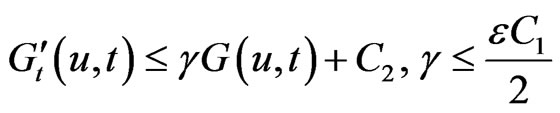 (6)
(6)
(H4)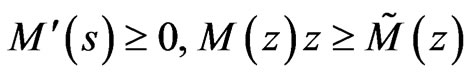 (7)
(7)
For simplicity, we define
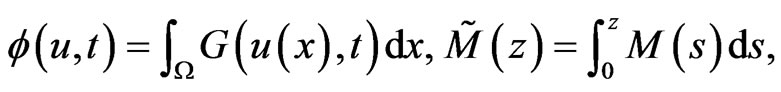
and
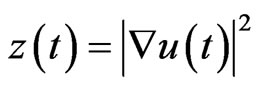
with the usual notation, we write 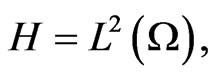
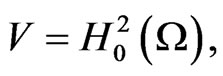
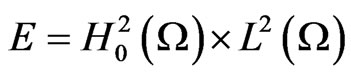 and the scalar products and norms on
and the scalar products and norms on 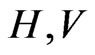 and
and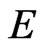 , respectively
, respectively
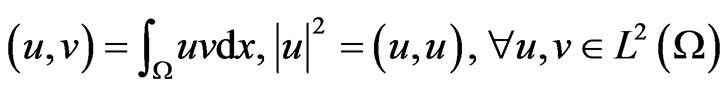

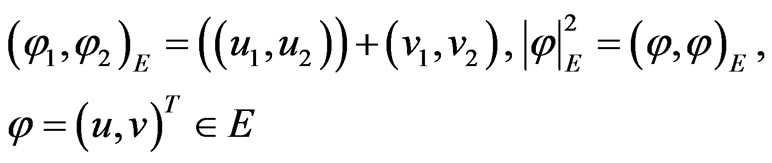
For the linear self-adjoint and positive operator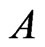 , let us write
, let us write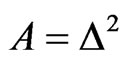 ,
,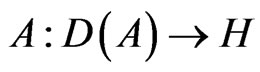 .
.
The space 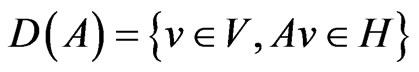 is dense in
is dense in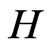 . Next, we define the power
. Next, we define the power 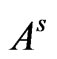 of
of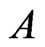 ,
, 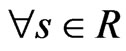 , which operate on the spaces
, which operate on the spaces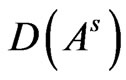 , and write
, and write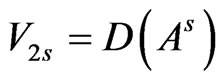 , which turns out to be a Hilbert space with the inner product and the norm
, which turns out to be a Hilbert space with the inner product and the norm
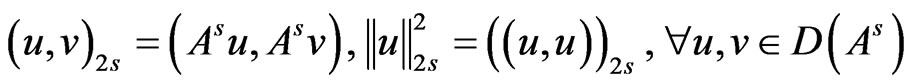
and 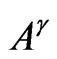 is an isomorphism from
is an isomorphism from 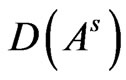 onto
onto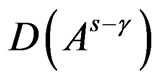 ,
, .
.
From the Poincaré inequality, there exists the constant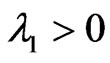 , such that:
, such that:
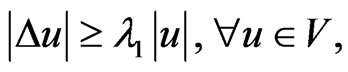
where 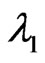 is the first-eigenvalue of
is the first-eigenvalue of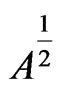 . For
. For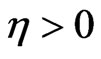 , we consider the abstract Cauchy problem on
, we consider the abstract Cauchy problem on 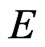 in the unknown variables
in the unknown variables 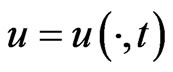
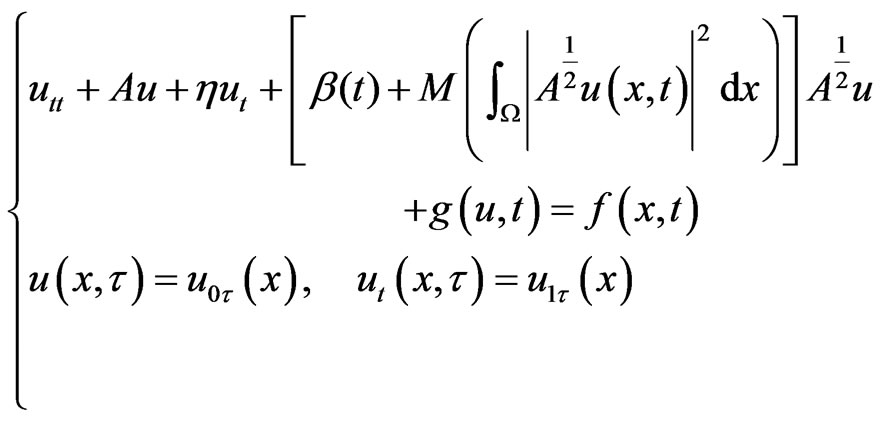 (8)
(8)
The following well-posedness result holds.
Theorem 1. Suppose that 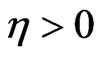 and the conditions (4)-(7) hold. If the nonlinear functions
and the conditions (4)-(7) hold. If the nonlinear functions 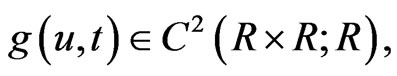
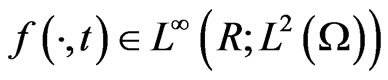 . Then, for any initial value
. Then, for any initial value 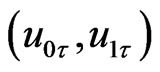 is given in
is given in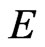 , problem (8) admits a unique solution
, problem (8) admits a unique solution 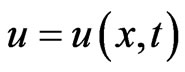 in the class
in the class
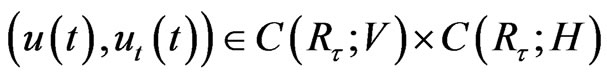
where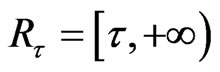 .
.
Furthermore, calling  the difference of any two solutions corresponding to initial data having norm less than or equal to
the difference of any two solutions corresponding to initial data having norm less than or equal to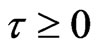 , there exists
, there exists 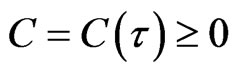 such that
such that
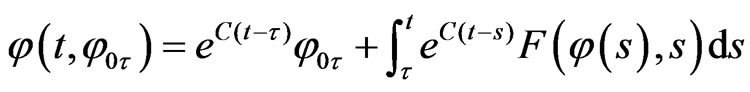 (9)
(9)
We omit the proof, based on a standard FeadoGalerkin approximation procedure together with a slight generalization of the usual Gronwall’s lemma. Theorem 1 translates into the existence of the solution operators
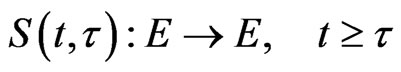 acting as
acting as
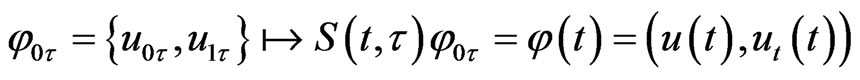
Remark 1. In the non-autonomous case, namely, when both 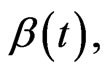
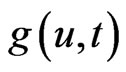 and
and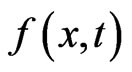 are time-dependent, the two-parameter family
are time-dependent, the two-parameter family 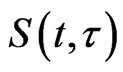 fulfills the semigroup property
fulfills the semigroup property
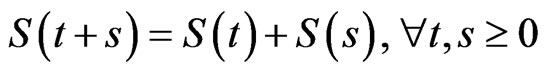 .
.
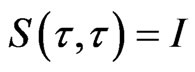 is the identity operator,
is the identity operator, .
.
Thus, 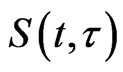 is a continuous semigroup of operators on
is a continuous semigroup of operators on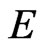 .
.
3. The Absorbing Set
In this section, we prove the existence of an absorbing set for the semigroup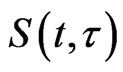 . Combining with (4) and (5), there exist two constants
. Combining with (4) and (5), there exist two constants 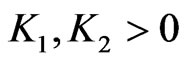 such that
such that
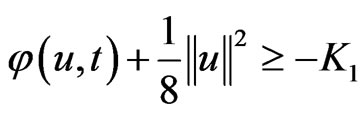 (10)
(10)
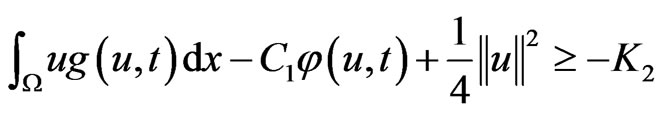 (11)
(11)
Lemma 1. Under the hypotheses of Theorem 1, For the ball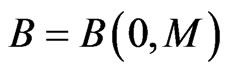 ,
,  , centered at 0 of radius M, is an absorbing set for the semigroup
, centered at 0 of radius M, is an absorbing set for the semigroup 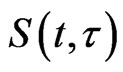 in E.
in E.
Proof. Let us begin with 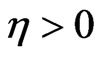 be fixed and
be fixed and 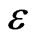 is chosen such that
is chosen such that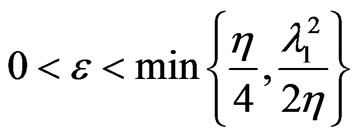 . We set
. We set
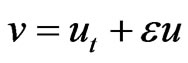 and rewrite (1) as follows
and rewrite (1) as follows
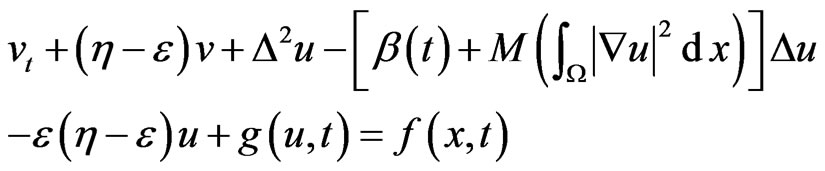 (12)
(12)
Taking the scalar product in H of (12) with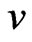 , and we obtain the desired form
, and we obtain the desired form
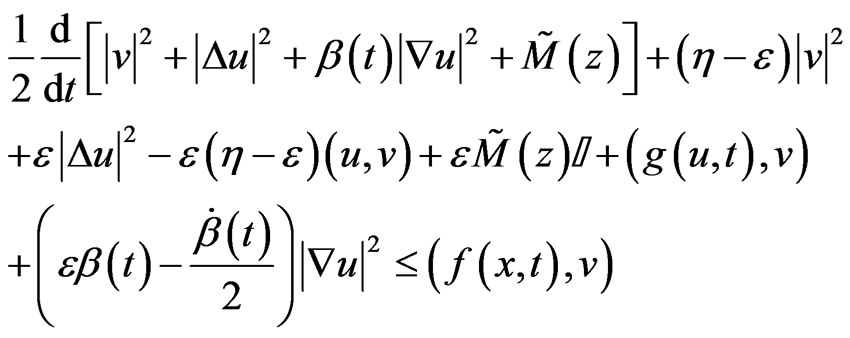 (13)
(13)
Using the Hölder inequality and the Poincaré inequality, we have the estimate
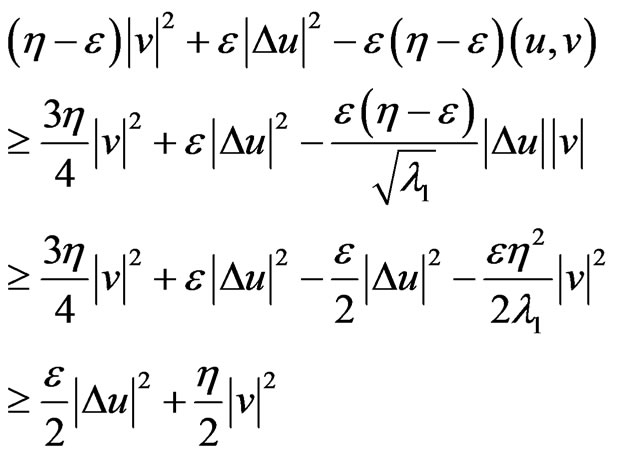 (14)
(14)
Exploiting (11), we lead to
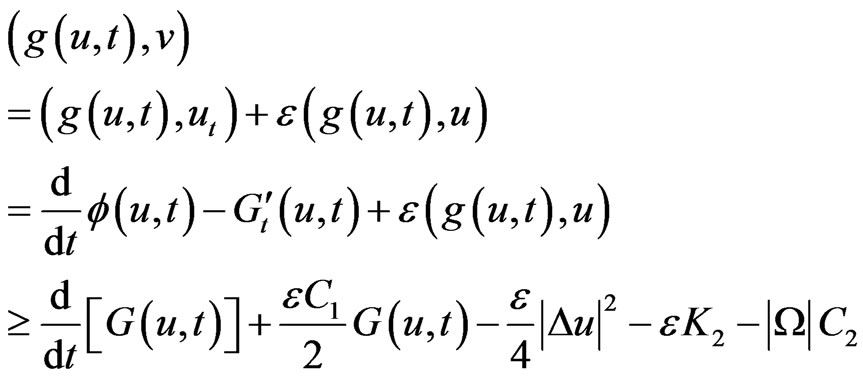 (15)
(15)
and,
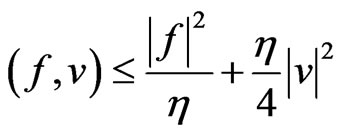 (16)
(16)
where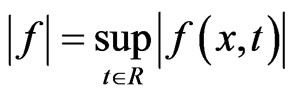 . From (13)-(16), it follows that
. From (13)-(16), it follows that
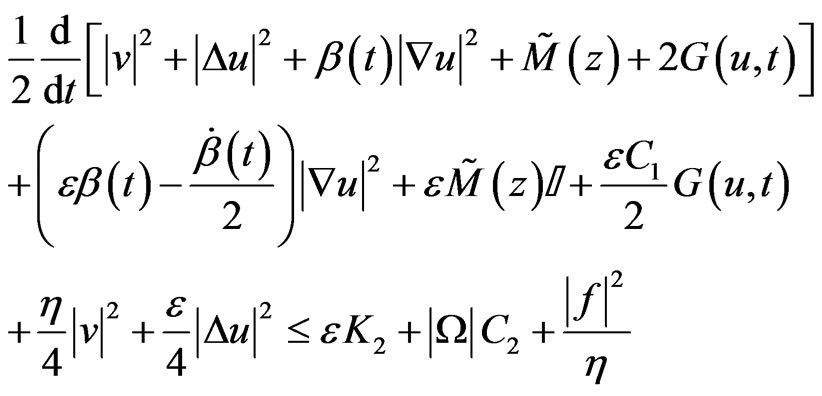 (17)
(17)
So, in the light of condition (10), we have
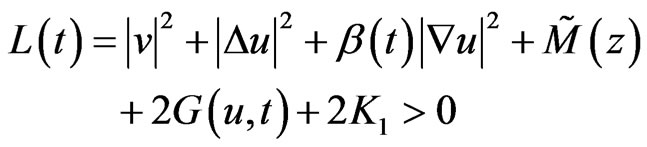
Taking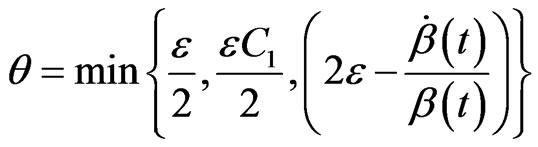 , we obtain
, we obtain
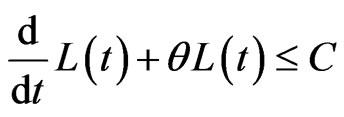 (18)
(18)
where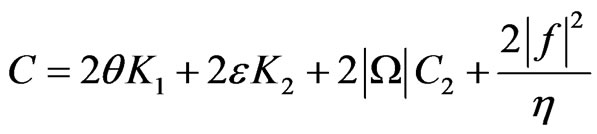 .
.
Applying the Gronwall’s Lemma, we obtain the following absorbing inequality
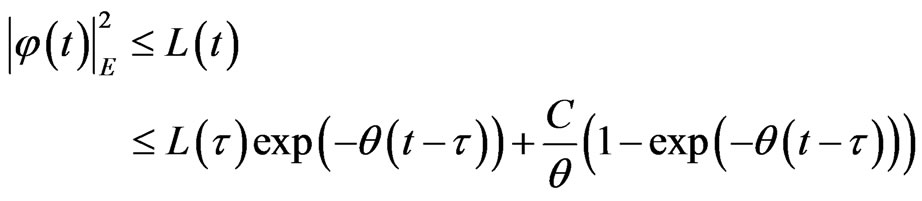
or
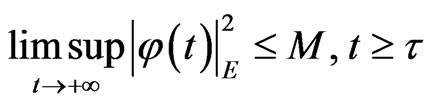 (19)
(19)
Taking
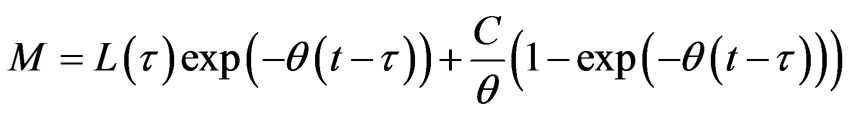 .
.
Obviously,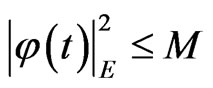 . Furthermore, let us denote
. Furthermore, let us denote 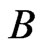 be a bounded closed ball of
be a bounded closed ball of 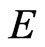 centered at 0 with radius
centered at 0 with radius 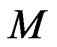
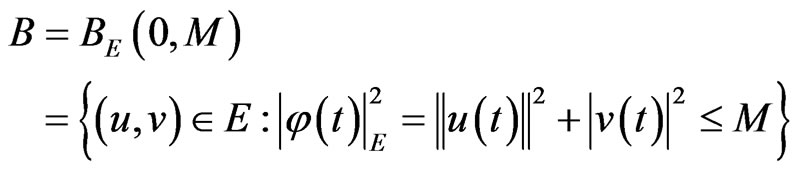
So, 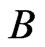 is a bounded absorbing set of analytic semigroup
is a bounded absorbing set of analytic semigroup  of (1)-(3). We complete the proof.
of (1)-(3). We complete the proof.
4. Continuity of the Semigroup
In this section, we prove the continuity of the semigroup  in
in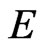 . For this reason, we assume
. For this reason, we assume
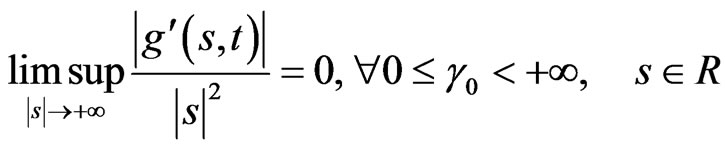 (20)
(20)
Lemma 2. Under the hypotheses of Theorem 1, the mapping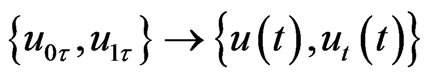 , for
, for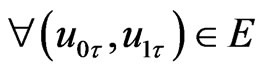 , is continuous in
, is continuous in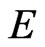 , and the semigroup
, and the semigroup 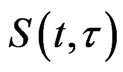 associated with the initial-boundary value problem (1) is a
associated with the initial-boundary value problem (1) is a 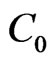 -semigroup in
-semigroup in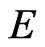 .
.
Proof. Assume that 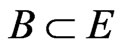 be a bounded positive invariant set for
be a bounded positive invariant set for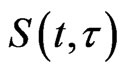 , and initial-data
, and initial-data 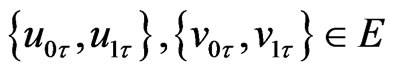 . Let
. Let 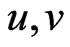 be the two corresponding solutions of (1).
be the two corresponding solutions of (1).
Assume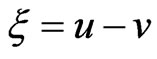 . We claim that the proof is similar to the Lemma 1. Then, from (1) we have
. We claim that the proof is similar to the Lemma 1. Then, from (1) we have
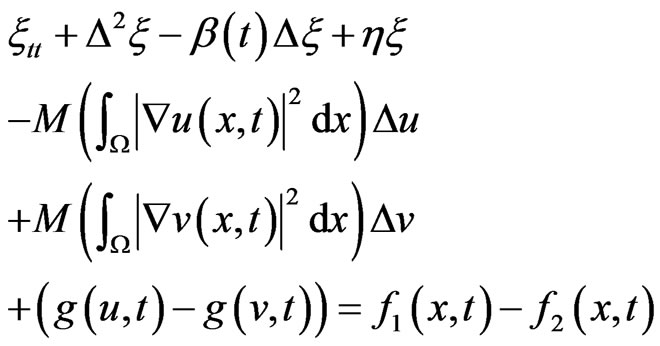 (21)
(21)
By multiplying (21) by 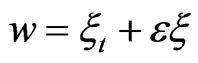 and integrating over
and integrating over , we find
, we find
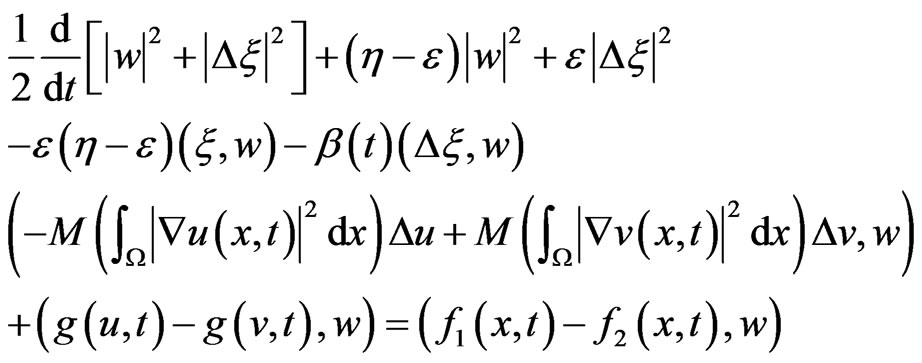 (22)
(22)
Next, we are devoted to estimate (22). By the same method that we obtained (14), it follows that
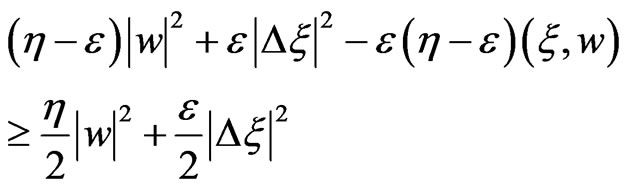 (23)
(23)
And, according to (20), for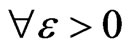 , there exists a constant
, there exists a constant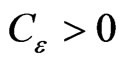 , such that
, such that
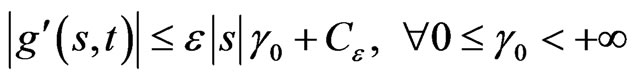 (24)
(24)
By (24) and the Sobolev embedding theorem, we can obtain 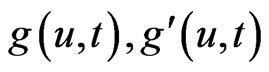 are uniformly bounded in
are uniformly bounded in , that is, there exists a constant
, that is, there exists a constant , such that
, such that
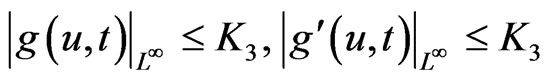 (25)
(25)
From (24), (25), it follows that
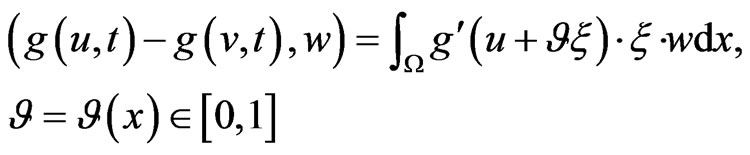 (26)
(26)
Thus
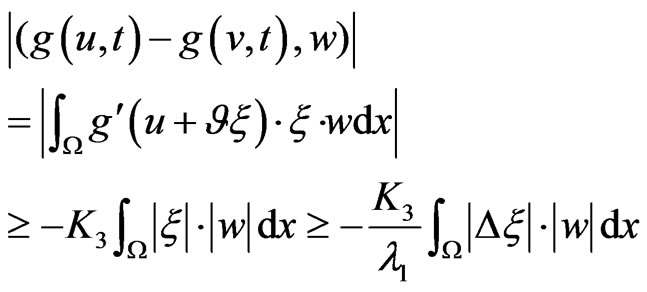
Meanwhile, we know easily
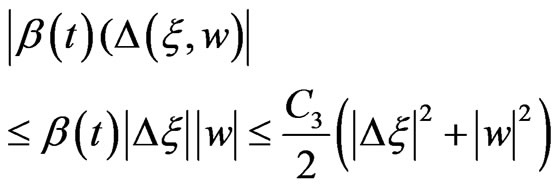 (27)
(27)
Due to the continuity of , we can note the fact that
, we can note the fact that
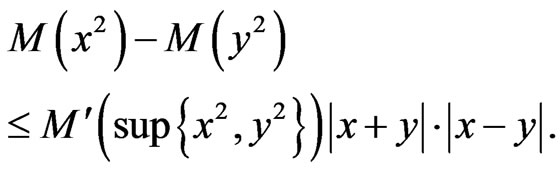
We see that easily
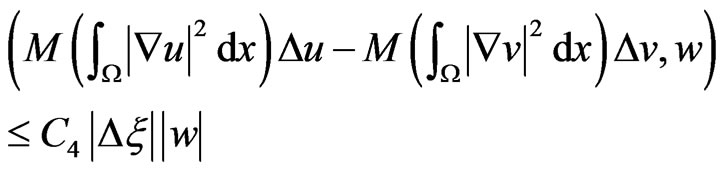 .
.
This implies
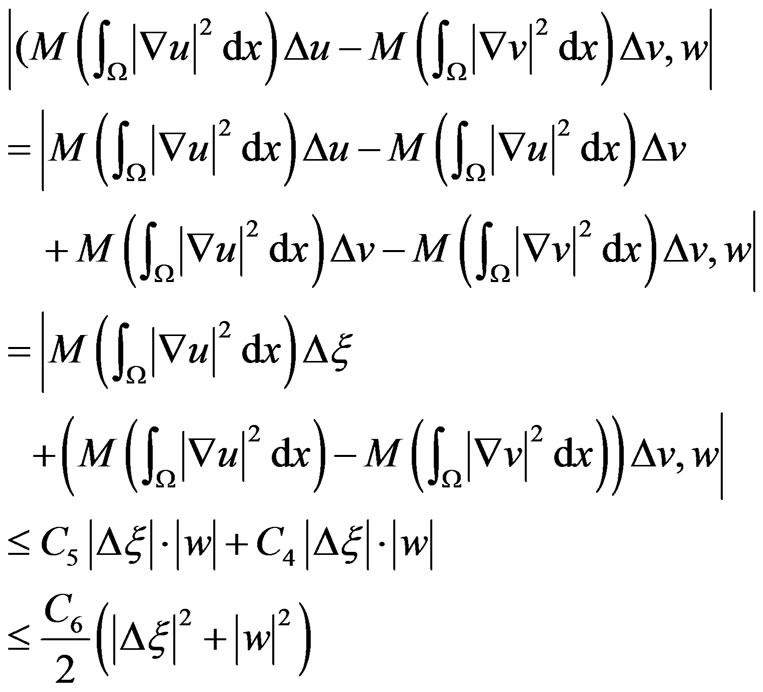 (28)
(28)
where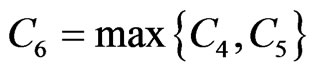 .
.
Combining with (27) and (28), it is obtained directly
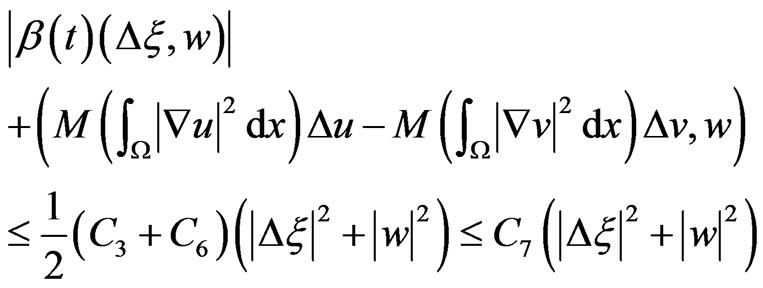 (29)
(29)
Thanks to (22)-(29), and the usual Gronwall’s Lemma, we have
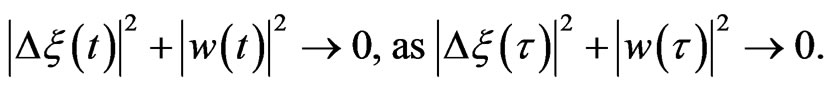
So we complete the proof.
5. Existence of the Global Attractor
Theorem 2. Under the hypotheses of Theorem 1, the semigroup  associated with the initial-boundary value problem (1) possesses a global attractor
associated with the initial-boundary value problem (1) possesses a global attractor  in
in 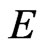 which attracts all bounded subsets of
which attracts all bounded subsets of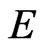 .
.
Proof. Let 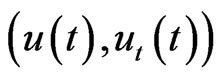 be a solution of (12) with initial value, for any
be a solution of (12) with initial value, for any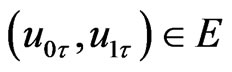 , and, it can be decomposed into
, and, it can be decomposed into 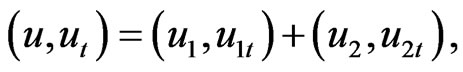 where
where 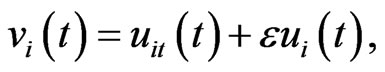
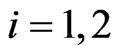 , satisfy, respectively,
, satisfy, respectively,
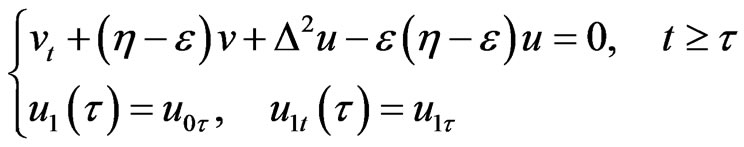 (30)
(30)
and
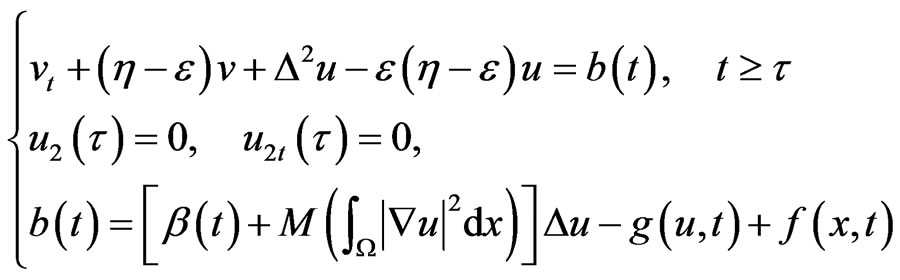 (31)
(31)
Applying two lemmas showed below. We also define a new inner product and norm in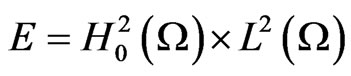 . Obviously, by embedding theorem, (30) are easily concluded through some simple computation
. Obviously, by embedding theorem, (30) are easily concluded through some simple computation . It is sufficient to prove that
. It is sufficient to prove that  is asymptotically smooth in
is asymptotically smooth in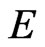 .
.
Taking the inner product in 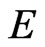 of (12) with
of (12) with 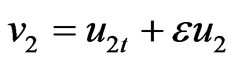 , we obtain
, we obtain
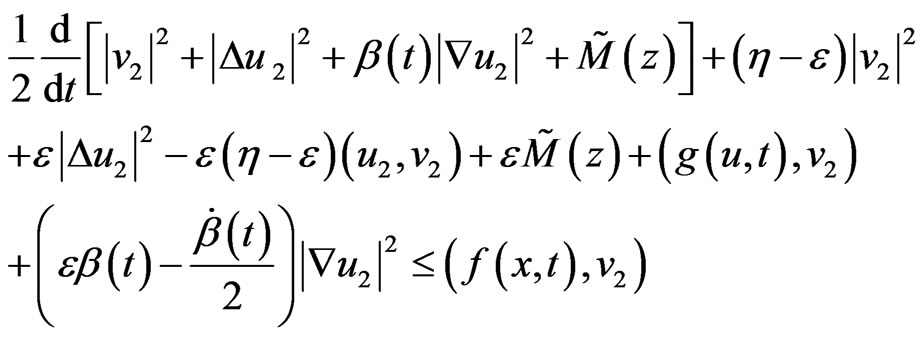
According to the uniform boundedness of 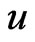 in space
in space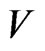 , the Sobolev Embedding theorem and the Gromwall’s Lemma, combining with Lemma 1, we have the conclusion similar to below,
, the Sobolev Embedding theorem and the Gromwall’s Lemma, combining with Lemma 1, we have the conclusion similar to below,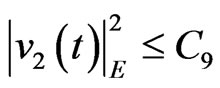 . Thus, this leads to
. Thus, this leads to 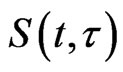 possesses a global attractor
possesses a global attractor 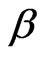 in
in 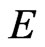 which attracts all bounded subsets of
which attracts all bounded subsets of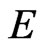 . So we end the proof.
. So we end the proof.
REFERENCES
- S. Woinowsky-Krieger, “The Effect of Axial Force on the Vibration of Hinged Bars,” Journal of Applied Mechanics, Vol. 17, 1950, pp. 35-36.
- O. F. Ma, S. H. Wang and C. K. Zhong, “Necessary and Sufficient Conditions for the Existence of Global Attractor for Semigroup and Application,” Indiana University Mathematics Journal, Vol. 51, 2002, pp. 529-551. doi.org/10.1512/iumj.2002.51.2255
- R. Temam, “Infinite Dimensional Dynamical System in Mechanics and Physical,” 2nd Edition, Spring-Verlag, Nork York, 1997.
- Q. Z. Ma and C. K. Zhong, “Existence of Strong Global Attractors for Hyperbolic Equation with Linear Memory,” Applied Mathematics and Computation, Vol. 157, No. 1, 2004, pp. 745-758. doi:10.1016/j.amc.2003.08.080
- Q. Z. Ma and C. K. Zhong, “Global Attractors of Strong Solutions for Nonclassical Diffusion Equation,” Journal of Lanzhou University, Vol. 40, 2004, pp. 7-9.
NOTES
*This work is supported by the School Foundation of TUT (900103- 03020715) and the Provincial Natural Science Foundation of Shanxi (2010011008) and (2011021002-2).
#Corresponding author.

