ABSTRACT

The amount of fine material available in the soil is significant in Atterberg limits and methylene blue tests. In the context of Atterberg limits, increased amount of clay minerals contained in the soil increases liquid and plastic limit values; however, increasing sand content reduces the moisture content reducing the water retention capacity of the soil which in return reduces the plasticity index (PI) value. In the case of methylene blue test, which is used to specify the quality of the amount of fine material, existence of clay in the medium increases the pollution level of the sand and the amount of methylene solution (V₁) used. In this study, soil classes were determined and pollution rates were identified with Atterberg limits, pycnometer, sieve analysis, hydrometer analysis and methylene blue tests conducted on 11 different natural soil samples collected from different regions. From the data obtained, first the relationship between PI and methylene blue (MB) was examined and was evaluated according to the results of the “single regression” method. Furthermore, the other coefficient of uniformity (C_u), coefficient of graduation (C_c), unit weight of soils (γ_s) parameters obtained from experimental studies were also subjected to “multiple regression analysis” in order to reveal their impact on the MB and this impact was confirmed taking both statistical analyses into account.

Keywords:

Atterberg Limits, Sieve and Hydrometer Analysis, Pycnometer Test, Plasticity Index, Methylene Solution Amount (V₁)

1. Introduction

Soil is a material which may also include organic matter and which is generated as a result of the mechanical disruption of the Earth’s crust by the erosive effects of water, ice and wind or by chemical processes which create solid grains and patches of water and/or air between them [1] [2] . Solid phases consist of solid particles of inorganic and organic character. Liquid phase, on the other hand, is usually an aqueous electrolyte solution. Depending on the biological activity in the soil and its location along with the effects of its contact with the atmosphere, the gas phase may have a different secondary composition [3] . Soil, as a result of several different materials it contains, emerges as a carrier material beneath the foundation of structures and as a material used to produce soil structures (earth dam, land reclamation, banks, etc.). It is also used as a filter, subjected to injection, and also used in groundwork as an aggregate for concrete [4] . In civil engineering, geotechnical engineers use large numbers of processed soils as building material in many cases [5] . Therefore, it is necessary to find relevant parameters for an engineering design and to develop a behavioral model for all soils in order to analyze the behavior of soils under the load of the land [6] . This, in return, makes it necessary to classify soils according to some of their similar engineering properties behaviors [7] . For this reason, Atterberg limits, sieve and hydrometer analyses are crucial in soil classification.

Also known as limits of consistency, “Atterberg limits” were first proposed by Atterberg (1911) [8] [9] . Atterberg limits define the condition of the soil with respect to the relationships between the grain content of the soil and the water and the changing water content [10] . Seybold et al. [11] , defined the limits of consistency as the limit moisture content which is the degree of resistance against deformation in the classification of water content of the soil, and emphasized the importance of the role they play in the classification of swelling potential and cohesion of the soil along with factors used to describe the soil such as shear strength, bearing capacity, and compressibility [11] . Moreover, Atterberg limits are the lower and upper limits, namely, liquid (W_L = LL) and plastic limit (W_P = PL) values, which define the plasticity of fine-grained soils, and bear great importance in the assessment of some engineering properties of the soils. These parameters are calculated based on the type of clay mineral, its structure, the type of the variable cations and the amount of organic matter available in the [12] [13] . Especially the liquid limit may vary depending on the physical properties such as soil structure, intensity of the surface load, water equivalent thickness and the shape of the grains and chemical properties [12] . Plastic limit (LL-PL) refers to the plasticity index (PI) in terms of moisture content. Plasticity, on the other hand, is the ability of the soil to be exposed to a deformation which cannot be reversed without cracking or breaking at a constant volume [11] .

Limits of consistency are a feature of clay and silts which are classified under fine-grained soil group and as one may know these soils absorb water and they can be found in various phases such as solid or liquid depending on their water content [14] .

Thus, it is possible to explain limits of consistency in terms of the “volume (V)- water content (W) relationship” (Figure 1). A cohesive soil, when absorbed excessive amounts of water, loses its shear stress while obtaining viscous properties. Such a viscous soil will exhibit plastic properties and therefore can be shaped easily without failures and cracks when it is cured for a specific amount of time [15] and recovers its shear stress at a specific amount. The water content in this transition phase is called liquid limit, (W_L). If the water is further removed, then the soil will lose its plastic properties gradually and it will crumble when rolled on a flat surface; the water content of this condition is called plastic limit, (W_p). An even further reduction of the water content will no longer lead to a reduction in the volume and the soil will exhibit a brittle behavior; the water content of this condition is called water retention or shrinkage limit (W_R = R_L) [9] . Briefly, liquid limit is the water content at which liquid changes its phase from liquid to plastic; plastic limit is the water content at which soil changes its phase from plastic to semi-solid; and shrinkage limit is the water content at which soil changes its phase from semi-solid to solid [9] [11] .

As shown in Figure 1, volume decreases as the water content is reduced, however, volume is constant after a specific point as the water content is further reduced. This transitional water content is the minimal water content where the soil is saturated with water [15] [16] .

A review of the standards for limits of consistency measurements reveals that the measurement is commonly conducted on the soil passing through #40 mesh. However, fine-grained sand is also among the soil group which is able to pass through this sieve [14] . As shown in Figure 1, the most important property of fine-grained soil is that it behaves differently according to its consistency. However, this is not the case for coarse-grained soils [17] . In order to clarify this point, a number of relevant studies are explored below.

Gündüz and Dağdeviren (2009), explored the impact of grain size and its amount on some parameters of fine-grained soils. Their findings showed that sand grains available in the soil significantly reduce the liquid and plastic limit values, in other words, amount of water needed for the medium to change its

phase to liquid, and that the soil class itself can be changed according to the plasticity value fine-grains actually have. Nevertheless, during the experiments it was also observed that some of the samples could become non-plastic (semi- solid transition without plastic behavior) with the effect of increased sand content. Therefore, it was claimed that liquid and plastic limit measurements must be conducted on the fine-grained soil which passes through #200 sieve, in order to eliminate some of the negative effects that may occur [13] .

Topçu (2011), reported that miscalculation of the plasticity value of the soil could lead to serious problems in engineering applications. In his study, Topçu showed that liquid and plastic limits of material accumulated under # 200 sieve were significantly higher than the material accumulated under #40 sieve, and suggested that that the reason behind this difference is the increase in the specific surface of the soil [18] .

Also important for soil classification is sieve and hydrometers analyses, as well as Atterberg limits.

The sieves used in sieve analysis usually consist of square meshes and the width of these square meshes are called mesh diameter. The finest sieve used in the soil survey mechanics is the sieve #200. Material passing this sieve are classified under silt and clay, while sand and pebbles are not able to pass the sieve. Therefore, 200 sieve is used to separate fine-grained and coarse-grained soil while 40 sieve is used to separate sand and pebbles. Sieve analysis helps us define the grain size distribution of the grains larger than the mesh size of 200 sieve (0.074 mm).

Hydrometer analysis is also a method used to determine the grain size distribution of the fine-grained soils passing through 200 sieve and to find the weight percentage of the clay-silt group in the soil. Sedimentation analysis is based on the Stokes law, which gives the relation between the rate of sedimentation and the diameter of spherical sediments in a liquid [6] . According to the Stokes Law, the specific weight is the same as that of the grain and equivalent sphere diameter is taken as the grain diameter of the grain with the same rate of sedimentation [19] while different grain sizes lead to different rates of sedimentation [6] i.e., coarse-grained material sediments faster than fine-grained material [19] . However, the Stokes Law applies only for spherical grains and it should be noted that the hydrometer analysis gives approximate results due to the fact that the silt and clay grains have a laminar structure (plate form) [6] .

Methylene blue point test, on the other hand, is used to determine the clay content of concrete and mortar aggregates which is available between fine grains below 0.063 mm in diameter. It also allows the determination of ion adsorption capacity of the soil with the specification of the amount of methylene blue required to cover the entire surface area of the clay grains available in the soil. This test determines the amount of harmful clay minerals but cannot determine the rate of damage they are able to cause. Presence of excessive amounts of clay minerals in the concrete increases the amount of water needed for concrete and mortar, which leads to impaired hardened concrete and mortar strength, their durability and volumetric stability [20] .

Chiappona et al., (2004) conducted a series of studies on the applicability of the methylene blue test used to define clay minerals as suggested by the standard methods used in France and the US and the findings of these studies showed that the test method defined by the US standards is suitable for fine and homogeneous material, in other words, they only provide information for the determination of the clay content, and that the test method, while the method defined by the French standard must be used on heterogeneous materials in order to provide information representing the material as a whole [21] [22] .

LL, PI, engineering classifications and other engineering properties are parameters used in the ground survey to define the soil. However, identification of LL and PI is not a part of routine soil study definition analysis, and is expensive and time consuming. These are conducted only once, and such data are not generally useful [11] . Traditionally, manually manipulating the liquid limit and plastic limit data for the soil (attempts to improve) can cause significant failures [23] . There is still a need to have a universally applicable, fast and reliable method in LL and PI estimations for soil surveys [11] . In general, LL and PI must be predictable from the soil properties obtained from soil surveys However, today there is no object-oriented visual program available for this purpose, which brings up the idea to use software to obtain high-efficiency and high-accuracy data and to use data improved by computer science. Currently, among the main algorithms used in order to improve the soil liquid limit and plastic limit data is analytical method, regression analytical method and least squares method [23] . In the light of all the aforementioned requirements, this study aims to offer an alternative to Casagrande method used in the LL and PI estimations. The reason behind this attempt is that many difficulties (wet or dry sample preparation, coating the sample into a brass vessel, opening a groove, ensuring sufficient material for coating, drop height between the brass vessel and plastic surface, etc.), operator mistakes, etc. faced in these experiments may lead to incorrect W_L results. Nevertheless, the fact that this is a time-consuming experiment design causes the water content of the samples to change frequently, which reduces the applicability of the method and reliability of the results. Therefore, it is aimed here to establish a correlation between the ratio of fine-grained particles and the pollution, having compared the plasticity index (PI) values and to use of methylene blue test results in the PI estimations.

2. Materials & Method

In this study, 11 different natural soil samples taken from different regions were used and these regions are shown in Figure 2 while Table 1 offers their geographic coordinates. Laboratory experiments conducted on each sample and the methods used are briefly described below.

In the pycnometer (specific gravity) experiment; samples were sieved using 40 sieve, then dried at 105˚C in a drying oven for 24 hours and the dried material was ground using a wooden mallet and 50 g of the sample passing 40 sieve was taken. Since the grain sizes of the soil samples used in the experiment were often small, only unit bulk density of fine-grained soil was identified using 500 ml density bottle and the process was conducted in accordance with ASTM D 854 [24] .

Soil class of the samples were defined using liquid limit and plastic limit tests, sieve analysis and hydrometer analysis in accordance with Unified Soil Classification System (USCS).

The liquid limit test can be carried out according to ASTM D 4318 [25] in two different ways, namely, wet and dry. In this study, 11 test samples were prepared according to dry sieving method and Casagrande method was used. Experiments were performed based on the ASTM D 4318 standards taking previous research to account and material accumulated under 200 sieve (100 g) was used.

Plastic limit test was also performed based on ASTM D 4318 standards using approximately 20 g of the mixture prepared for the liquid limit test, as plastic limit test is conducted in connection with the liquid limit test.

The sieve analysis test was carried out on a 500 g sample using 200 sieve in accordance with ASTM C 136 [26] and TS EN 933-10 [27] standards and the soil was washed as part of the process. 200 sieve is the thinnest sieve used in soil mechanics; the part of the soil accumulated on the sieve accounts for sand and pebble group while the material passing the sieve account for clay-silt group. The material accumulated on 200 sieve was analyzed in the sieve analysis while the material passing the sieve was dried for 24 hours in a drying oven in order to be used in the hydrometer analysis. The total weight of the material remaining on the sieve was then weighed and the percentage of loss during washing, that is, the total percentage passing the sieve was calculated.

During the hydrometer test, it was tried to adhere to the ASTM D 422-63 [28] standard as much as possible. As part of this test, the material passing 200 sieve (50 g) was used for washed sieve analysis in this experiment and the purpose of this experiment was to calculate the percentage of materials such as silt, clay, etc. by weight, utilizing their sedimentation rates. At the beginning of the experiment, readings were first taken at the time intervals specified in the standards. However, as the rate of sedimentation for clay and silt grains in water can change due to ambient temperature, decomposing agent, meniscus, etc., it is necessary to make necessary corrections on the first readings. Therefore, the attempts to keep the ambient temperature constant were futile in time (especially during lunch hours) and new hydrometer readings were obtained using meniscus adjustments. As no decomposing agent was used in the suspension prepared, no adjustments were done for this purpose. Effective depths (L), K factor and correction factor (α) values from the tables developed using the readings and standards are also used to calculate the percentages passing the screen.

Methylene blue test is conducted based on the principles and regulations of TS EN 933-9 + A1 [29] . In this experiment, methylene blue solution is prepared having 10 g ± 0.1 g methylene blue powder mixed with distilled water and stirring the mixture for 45 minutes at the room temperature. 200 g sample (M₁) with grain size of 0 - 2 mm is cured in a stove for 24 hour at 105˚C and then is allowed to cool to room temperature. The sample is then weighed after being cooled and transferred to a beaker after being blended using a spatula. Soil sample is stirred in a speed adjustable blender for 5 minutes at 600 ± 60 rpm after adding 500 ml distilled water. Next, 5 ml solution is added to the mix and blender is operated for 1 minutes but this time at 400 ± 40 rpm. After 1 minute of blending, one drop of suspension is extracted using a glass rod and dripped on a filter paper. Generally, the first drip will involve a dark blue stain and surrounding water circle. The process is repeated adding solution until a light-blue circle (halo) is obtained around the blue central stain. 5ml of solution is added in the first 5 minutes. After these 5 minutes, the amount of solution is reduced to 2ml and stirred for 1 minute and one drop of suspension is extracted using a glass rod and dripped on a filter paper in order to observe the circle formation. Experiment is completed when a light blue circle forms around the central blue stain and if it does not vaporize for 5 minutes and the total amount of volumetric solution is calculated in ml. (Light blue circle must be approximately 1mm in diameter for a central stain of 8-12mm diameter). The following equation was used in the calculation of MB to be used, and the results of the experiment are shown in Table 2. In addition, Figure 3 shows an exemplary application for the Sample #6.

(2.1)

Here;

MB = Methylene blue value (%);

V₁ = Total volume of the methylene solution added (ml);

M₁ = Mass of the experiment sample (g).

Factor 10 = A factor used to convert the volume of stain solution used to the mass of stain per kilogram of the mass tested (TSEN 933-9+A1) [29] .

3. Experiment Results

3.1. Pycnometer Test Results (Unit Weight of Solids)

Pycnometer test was conducted in order to be used in hydrometer analysis in

accordance with ASTM D 854 and the specific bulk density of the soils tested were found to be in the range of 2.4 - 2.8 g/cm³. The results are shown in Table 3 below.

3.2. Atterberg Limits Test Results

Liquid limit tests were performed until at least 3 - 4 pulses were detected in the range of 10 - 40 while the plastic limit tests were conducted twice paying attention to at least 6g sample available in each container. Then, the test results are plotted in tables created in MS Excel and the number of pulses obtained is plotted logarithmically in x axis while the corresponding water content (W) is plotted in y axis in order to derive a flow curve. In this flow curve, the value of the water content corresponding to 25 pulses gives us the “liquid limit” value of that soil. In all experiments, the W_L value was found both with an “estimated” value calculated by the system and a manual drawing on the flow curve. Plasticity index is calculated on the basis of manual calculation from values obtained and these were compared against estimated values. Compatibility mode (correlation) for W_L values calculated by the system for each one of 11 tests was in the range between 92.3% and 99.5%. The main purpose here was to establish the correlation between the ratio of fine-grains and the pollution comparing the PI values and the percent of methylene solution used and the results of this comparison are addressed in the methylene test results section. Liquid limit and plastic limit test results are shown in Table 3.

3.3. Sieve and Hydrometer Analysis Test Results

In this study, the same soil samples are used for all experiments, experiment results of sieve and hydrometer analysis assessed in combination and soil class comparison was made in accordance with TS 1500/1900-1 [30] [31] /ASTM D

2487 [32] standards. First, grain diameter obtained from sieve analysis and hydrometer test was plotted logarithmically on the x axis while corresponding percentages passing the sieve were plotted on the y axis in order to give a granulometry curve.

C_u and C_c values were obtained using the granulometry curve, having identified the diameters of D₆₀, D₃₀ ve D₁₀ which corresponds to the material passing the sieve at the percentages of 60%, 30%, 10%, respectively (Table 3). Here, D₁₀ is the effective diameter while D₅₀ is the average grain size. In the soil classification, coarse-grained soils were classified using the correlations available in the USCS (ASTM D 2487) [30] where in fine-grained soils were classified using the plasticity graph.

Here, soil sample #8 is the only coarse-grained soil sample, and was classified under sand as more than 50% of its content passed the sieve and is represented with an “S” symbol.

C_u and C_c coefficients for pebble and sand are as follows for sand (sample #8);

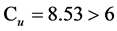
C_c = 0.79 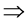and is referred to as “SP” as it does not meet the 1 < C_c < 3 condition (Table 3).

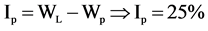
“SC” symbol was used as the Atterberg limits are above the A line or I_p > 7. Hence, the class of the soil sample #8 is assigned as “bad-graded argillaceous sand”.

Soil classes of the remaining 10 test samples were determined using the plasticity graph. The point where W_L and PI values of these soils were intersected was identified as the class of the soil.

3.4. Methylene Blue Test Results

Methylene blue test was conducted on 11 test samples with regards to the principles and regulations of TS EN 933-9 + A1: 2013 (2014). With this experiment, pollution levels of fine-grained soils were defined in an attempt to establish the correlation between PI values of the same soil sample.

4. Results of the Analysis

4.1. Estimation of the Plasticity Index Values According to the Results of Methylene Blue Test Using a “Single Regression Analysis”

Two different comparisons were made in the above Table 4 and Table 5; the first is based on the results from estimated and manual tests for 11 experiments while the second is based on estimated and manual tests for 9 experiments. Here, it was attempted to identify the relationship between these two parameters using the PI and MB values and “single regression” method. As shown in Table 4, the compatibility between the two parameters for the experiment involving 11 tests was R² = 0.7316 and the correlation was found to be y = 1.746x^0.664. On the other hand, the compatibility of the second comparison was reduced to R² = 0.7118

and the correlation was found to be y = 1.6148x^0.6811. A closer investigation of the plasticity values shows that the effect of the experiments # 4 and #8 diminishes the magnitude of the correlation. Therefore, a second comparison was made using both test results and the resulting “estimated” results gave a correlation of R² = 0.8544 while “manual” results gave a correlation of R² = 0.843 which was then translated into y = 1.1097x^0.7837 and y = 1.0014x^0.8037, respectively.

In other words, it is necessary to investigate the factors influencing the calculation of PI and MB while exploring the relationship between these two parameters. For example, values such as W_L and W_P which are used in the calculation of PI may result in incorrect results as they are affected by many factors such as the sample preparation method followed and the experience of the operator, etc. (as it was the case in experiments #4 and #8). Moreover, different W_L values were obtained from the estimations of the system and the manual drawing on the flow curve using the experiment results. In Table 4 and Table 5, although 2 experiment results were excluded due to incorrect W_L values manually calculated by the operator, a reduction in the correlation was observed in both cases. However, a higher R² value was obtained from the multiple regression method applied based on the manually calculated PI values available in Table 6 and Table 7. In the light of aforementioned outcomes, it was aimed to reach at a more reliable result with two comparisons on Table 4 and Table 5.

4.2. PI Value Estimation Using MB, C_u, C_c and γ_s Parameters with “Multiple Regression Analysis”

Multiple regression analysis is a method used to explain the cause-effect relationship between two or more independent variables which affect a variable and to determine the impact level of these independent variables. Multiple regression model calculations as well as in the establishment of prediction equations made just a single model and calculating the coefficients of variation from the average of the arguments being used. Formula describing the explaining the relationship between dependent and independent variables is as follows;

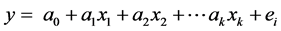(4.1)

Here;

x_i = Independent variables

y = Dependent variables

e_i = Error coefficient

Using the experimental data, such an investigation resulted in PI as the dependent variable and C_u, C_c, γ_s ve MB as independent variables (x). The modeling effort using these data gave a variety of statistics and their relationship with PI was explored. Using the coefficients of x₁, x₂, x₃ and x₄ variables and error coefficients obtained from the regression analysis, the formula gave the P-value, and this value was compared with the actual test results in order to calculate the compatibility coefficient (R²). Results for the 1^st variable;

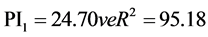
Same procedure was used also for the variables x₂, x₃ and x₄ and it was possible to identify the correlation between R² values and PI values of each dependent variable and the independent variable. This method was also repeated for 11 and 9 samples as it was the case for single regression method, and the R² values obtained for the first and second runs were R² = 0.75 and R² = 0.85, respectively. Briefly, using this method, it is possible to identify which independent variable(s) influence the dependent variable and to estimate the PI value using these variables.

5. Result and Recommendations

Liquid limit is an important parameter used to determine many indices and mechanical properties such as compression index, swelling percentage, soil class, liquefaction potential, etc. However, liquid limit and plastic limit test results may differ depending on several factors such as wet or dry sample preparation, the

operator errors that occur during experiments, time consumption, and excessive amount of water added. Therefore, alternative solutions are required establishing the relationship between the PI obtained from liquid and plastic limit tests and other parameters.

Higher clay-based material content of the soil increases the liquid limit and plastic limit in the case of limits of consistency while it increases the pollution level of the sand and V₁ used in the case of methylene blue test. This shows us that the increase in plasticity index depends on the liquid limit while the increase in liquid limit depends on the fine-grained content. In our experiments it was also found that V₁ increases as the PI increases in general, which can be interpreted as a negative relationship and a direct proportion between PI and MB values.

In this study, with this idea in mind, a relationship was observed between the amount of methylene solution used and PI value and “single regression” results showed that this result was statistically significant by 84.3%. Also using “multiple regression” method, the correlation between C_u, C_c, γ_s and MB parameters and the PI value was found to be very close to the one found using single regression and there was an increase, even if it was small. As it is possible to control more factors influencing the dependent variable (y) using more independent variables (x) in the multiple regression analysis, it is possible to include more variables to the model in order to explain the change in y more efficiently. In the light of this information, it is possible to say that the use of methylene blue test results in combination with a number of parameters can be used for PI estimations, which will result in more reliable results.

Here, the most important independent variable in PI estimation with the highest correlation was found to be MB (P < 0.05) as shown in Table 6 and Table 7. PI is significantly correlated with C_u, C_c and γ_s. Although C_u and C_c are important parameters in coarse-grained soil classification, they are not sufficient by themselves to estimate the PI. However, when assessed in combination with the PI, they can account for the fine-grained material available in the soil. Our main purpose here is to test the applicability of the methylene blue test as an alternative to the Casagrande method commonly used in PI calculations. And it was tried to emphasize the importance of the fine-grained material ratio available in the soil for both methods. The results of the experiments showed that the pollution rate and therefore the V₁ used increase as the PI is increased. Nevertheless, considering that the reason behind the difficulties in the liquid limit tests is the operator failure rather than the soil structure, it was concluded that MB (%) values can be used in the PI estimation.

Cite this paper

Otçu, N.Ü., Uzundurukan, S. and Kaplan, G. (2017) Determınatıon of the Plasticity Index of Soils with Fine-Grained Soils Using Methylene Blue Test. Journal of Geoscience and Environment Protection, 5, 165-181. https://doi.org/10.4236/gep.2017.53012

References