Open Journal of Civil Engineering
Vol.06 No.04(2016), Article ID:70989,15 pages
10.4236/ojce.2016.64054
Variable Thermal Comfort Index for Indoor Work Space in Office Buildings: A Study in Germany
E. Kuchen
Regional Institute of Planning and Habitat (IRPHa), Faculty of Architecture, Urbanism and Design, National University of San Juan, San Juan, Argentina
Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 11, 2015; Accepted: September 26, 2016; Published: September 29, 2016
ABSTRACT
International standards state the thermal comfort requirements that office spaces must comply with. These are based on a model developed by Prof. Paul Ole Fanger of the Centre for Indoor Environment and Energy, Denmark. Today, forty-year research shows an evolution in these experiences. The work presented here is to develop a tool to evaluate the thermal comfort of working environments of office buildings. A methodology is devised on the basis of on-site measurements and questionnaire responses. For measurements, a mobile unit equipped with sensors is used, whereas the questionnaire obtains user responses on thermal quality of the work space. The thermal conditions of thirty office buildings presenting different acclimatization systems have been surveyed. The correlation between objective and subjective data allows developing a formula that shows the thermal comfort level for a given environment as a function of local aspects. For the surveyed buildings, the resulting comfortable temperature was 23.3˚C, and the minimum percentage of user individuals experiencing discomfort with such temperature was 7%.
Keywords:
Field Work, PPD-Index, Neutral Temperature, Thermal Sensation, Thermal Preference

1. Introduction
The quantitative definition of thermal comfort for any given space can be stated by applying the PPD Index (Predicted Percentage of Dissatisfied) as proposed by the standard [1] . This index is built upon a mathematical model developed by Fanger using data from experiences made with humans in a controlled climatic chamber. The individual responses render a thermal sensation vote which is then related with the corresponding operative thermal measurement readings [2] . The model responds on a small sample of people sharing a pre-defined thermal environment. This means that, while the operative temperature is varied in the 66 to 90˚F (18.9˚C to 32.2˚C) range, the remaining physical parameters affecting the thermal comfort (e.g., air speed and humidity) and the person’s physical and physiological factors (clothing insulation and activity levels) are kept constant.
Research results from [3] and [4] have shown that the user’s behavior indicates that even in spaces having constant thermal conditions, they are capable of experiencing adaptation processes which allow them to accept thermal conditions imposed by the building manager controlling the HVAC system. Other authors [5] [6] state that personal factors, such as body build-up, gender and food intake and close vicinity parameters, such as the external climate, affect the thermal perceptions of persons. According to these authors, the users express a critical attitude of the thermal environment conditions that is then translated into a continuous adaptation process [7] - [9] .
Various field works have shown that there is an interrelationship between climatic and non climatic factors and their influence on thermal comfort in actual work spaces. Several authors [10] - [14] state that the use of standards, such as [1] , based on Fanger’s model, evinces deviations stemming from causes inherent to the very method used to attain it. Besides, these approaches become constrained when trying to have a holistic vision on comfort, and they are certainly useful only when the internal conditions are kept constant and within pre-established ranges. They show, moreover, that the adaptation capability of users to the various thermal environments is not considered in the experiments made in climatic chambers.
The method presented in this paper is based on making measurements and having the space users fill questionnaires simultaneously to the measuring sessions carried out as a field work in 30 building offices in Germany [3] [4] . Measurements are made with a mobile unit equipped with high-precision sensors, and the questionnaire contains questions on thermal aspects of their work space. Through the user vote, these results are translated into a value scale. Results evaluations show strong correlations among the mean vote on thermal sensation, the mean vote on thermal preference and the operative measured temperature readings.
As a contribution, the work defines criteria on thermal neutrality (thermal satisfaction). Besides, a model is developed to predict the variable thermal comfort in office buildings and a methodology is devised to elaborate computational tools for professionals working in this disciplinary area. These tools should help address the monitoring and evaluation of thermal parameters of real work space that may lead to establish indicators on the environmental quality of buildings.
2. Development
2.1. Office Buildings
The data base for the analysis is made up with information collected in 30 office buildings being not older than 10 years or renewed on the basis of international standards on energy efficiency. The buildings are subject to the Central European climate and are located in the German cities of Berlin (number of buildings, n = 9), Bonn (n = 1), Braunschweig (n = 5), Hamburg (n = 4), Hannover (n = 4), Gelsenkirchen (n = 1), Helmstedt (n = 1), Leverkusen (n = 1), Magdeburg (n = 1), Mannheim (n = 1), Osnabrück (n = 1) and Wolfsburg (n = 1). They are located between 48˚ and 53˚N latitude and 6˚ and 15˚E longitude. Some of these buildings are shown in Figure 1. Taking into account the premise of considering international standards and to obtain a reliable methodology and testing tools, the research work aims at stating that it is possible to discern about differences from among the strategies used for ventilation and acclimatization. To this purpose, the buildings have been discriminated into three categories or types: Type 1 (number of surveyed buildings, n = 8), Type 2 (n = 14) and Type 3 (n = 8). The building types are described below:
Type 1, T1 (non-acclimatized buildings). They feature only natural ventilation and they are apt to cover the heating requirements and to ensure the thermal comfort in winter (manually operated windows, heaters and heat radiators). This type of buildings is known as “free running or naturally ventilated buildings” [15] [16] .
Type 2, T2 (partially acclimatized buildings). They have heating and ventilation systems in part of the building, without air treatment other than the recycling air flow for thermal recovery. They feature radiant surfaces for heating/cooling in combination with radiators [17] . For ventilation, they have central mechanically-operated systems or decentralized ones (on façade openings) of low energy consumption and manually operated windows. As regards the buildings studied by other authors, this classification lies between the “free running building” and the “air conditioning building” [16] and [18] . Respecting the user's control on the internal climate, they resemble more likely to an “Alpha building” (high rate of user control on thermal conditions) than to a “Beta building” (low rate of user control on thermal conditions); see [19] .
Type 3, T3 (acclimatized buildings). Natural ventilation is restricted to only a mechanical ventilation system and high-performance and efficient air conditioning with air-flow feedback using hot/cool radiant surfaces. To a large extent, they present no operable windows, so the recycled air volume must be increased to maintain the air quality requirements. The building also features humidity control equipment with





Figure 1. Some typical examples of the 30 buildings chosen for this field study.
power enough for a fast response to changes made on indoor climate parameters. This flexibility implies making a significant investment on installation features and maintenance costs in order to ensure constant thermal conditions throughout the year [17] [20] . According to [16] [18] [19] , the building variant type T3 with manually-operated windows presents no significant difference with those of type T2. If they have no manually operated windows, these buildings are known as “air conditioning building” [15] [16] . As regards the users' control on the internal climate, they are rated as “Beta building” [19] .
2.2. Measurements
In order to read the climate parameters, a mobile measurement system (Mobile LAB, see Figure 2) allows carrying the instrument equipment (sensors) to each work space within the building. Measurements comprises three stages: First, in the morning until noon (12:00 AM); second, from noon until 2:00 PM in the afternoon, and the third stage from 2:00 PM on. This time partition allows collecting the interior climate parameters of each selected space during the work day, directly at the work post of the affected users.
Parameters are measured with high-precision sensors, with precision rating and response times that propose the standard [21] . The measuring time period is one minute. The mobile unit is equipped with sensors for air temperature (ta), operative temperature operative (top), dew point temperature (tdew), radiation asymmetry (∆tpr) and air flow speed (va) (see Figure 2). Measurement data are collected and transferred into a notebook processor.
The user is considered to be sitting and working and, therefore, the operative temperature sensor and most other measuring devises are placed within 1.1 m from the floor: Measurements begins after an acclimatization period for the sensors (3 minutes), lasting 5 minutes at most. Meanwhile, the user fills in the questionnaire for approximately 10 minutes. Five additional minutes are assumed to move the Mobile LAB
Figure 2. “Mobile LAB” Mobile measuring unit equipped with sensors to survey the climate parameters of each work post.
within the building. In general, up to four work spaces can be surveyed in one hour. The mobile unit was designed on the basis of the requirements of the [21] standard, and on the experience gathered after extensive field works [18] [22] [23] .
2.3. Questionnaire
The questionnaire is a subjective-type measurement that gathers diagnosis information given by the ordinary user. It contains questions on psychological, physiological and physical aspects linked to the user and the surrounding environment [3] . It is designed on the basis of the proposed objectives, and on other standardized models used in field works [15] [23] and [24] . From the questionnaire, the CV “Comfort Vote”, namely, the user’s vote on thermal sensation, is issued on a 7 point scale, originally defined by [5] and later re-defined by other authors as the ASHRAE scale, and verified through standardized scales of the norm [25] . Along this scale having two dissatisfaction poles, the user places his thermal sensation by choosing from a range that starts from −3 (cold), −2 (cool), −1 (slightly cool), 0 (neutral), +1 (slightly warm), +2 (warm) and ends at +3 (hot), with the possibility to choose intermediate ratings (see Figure 3). According to [26] , the use of the ASHRAE scale allows obtaining homogenous results. The CV allows, therefore, finding a thermally acceptable rage of temperature.
From the questionnaire, the PV “Preference Vote” (vote on thermal preference) allows finding a user preference and defining an index as a percentage of dissatisfied. The user chooses his/her thermal preference in a 3 point scale, verified with standardized scales of [25] , and based on the current conditions existing at the survey time. The thermal preference index works as a complement to the CV, and it is obtained from answering to “I would rather prefer a thermal environment that is”: with values ranging from −1 (cooler), 0 (neither cooler nor warmer = comfortable) to +1 (warmer), with no intermediate values to choose from (see Figure 4).
3. Results
3.1. Operative Temperature, top
The combination between air temperature (ta) and mean radiant temperature (tr), under a given condition for air flow motion (va), is translated as an integrated temperature known as the operative temperature (top). This value affects the user's overall perception of the thermal environment, and it is used as a parameter for evaluating the thermal comfort of indoor spaces. Regardless the ventilation and acclimatization factors, the Figure 5 shows the spread of the operative temperature in winter (number of mea-
Figure 3. The 7 point ASHRAE scale for the comfort vote.
Figure 4. 3-point scale to issue the Preference Vote desired for the thermal environment.
Figure 5. Operative temperature measurement for the seasonal periods of the year.
surements, n = 345), in the transient period (n = 457) and in summer (n = 546). In addition, the average value and the standard deviation for each period are presented as well. The standard deviation (σ) is an indicator of the spread of the collected data, and it represents the range where approximately 70% of the measurement data is lying, i.e., the most representative zone of the response sample.
The indoor climatic conditions vary upon seasons. The indoor operative temperature in winter reaches a mean value of 22.7˚C; with σ = 1.1. The maximum value for the season is 25.6˚C and the minimum 18.4˚C (see Figure 5). For the transient period, top reaches a mean value of 23.5˚C; σ = 1.2, with values max.28.5/min.20˚C. This expresses a major thermal transfer between internal and external climates, especially when opening windows [3] . In summer time, this exchange is intensified, with a mean value of top that increases some 25.3˚C; σ = 1.8; max.31.9/min. 21.0˚C. The large oscillations of top in summer arise basically in spaces of the type T1 buildings, with ample chances of affecting the thermal comfort of these work spaces. This situation and, moreover, the noticeable oscillations on operative temperature observed during the transient period and summer time call for a detailed analysis of the thermal sensation vote, as a function of the ventilation and acclimatization variants, so as to be able to know the meaning these temperatures imply for the space users.
3.2. Thermal Comfort Vote, CV
In this field work a total of 1100 questionnaires (votes) on thermal sensation for the sample of 30 office buildings have been collected. The observation on the behavior of the measured operative temperature and the comfort vote attained from the questionnaire is the starting point for evaluating the thermal comfort of real work space environments. The questionnaire (subjective measurement) and the survey on indoor climatic parameters with sensors (objective measurements) have been carried out simultaneously so as to discern the direct comparisons and find possible correlations. The users’ subjective rating allows finding the ranges where the operative temperature can be perceived as comfortable (neutral thermal sensation), high (warmth sensation) and low (cold sensation). For the analysis, the changes on the thermal conditions in the variants for ventilation and acclimatization are observed as well, as a function of the seasons.
Figure 6 shows that spaces in type T1 buildings undergo the greatest thermal annual oscillations of operative temperatures and thermal sensation. In summer, the average value of top for type T1 reaches 26.9˚C; σ = 1.9 and the mean comfort vote falls within the hot zone in the ASHRAE scale, with an average value of 1.20; σ = 1. In winter, top decreases to an average value of 22.1˚C; σ = 1.2 and the comfort vote drops to −0.13; σ = 0.9. As a contrast to the above, types T2 and T3 buildings show relatively constant thermal conditions, and the thermal comfort vote evolves around the neutral zone, very slightly offset towards the warm zone in the ASHRAE scale. This slight increment in operative temperature in these two building types in summer lies much below the values found for type T1.
The small fluctuations found in types T2 and T3 buildings turn it difficult to determine the level at which the users accept the thermal conditions, or whether they prefer a cooler or a warmer setting than what currently is set. This calls for considering the relationship existing between the thermal preference vote and the measured operative temperature. The standard deviation attained on the studied variables allow strengthening the hypothesis stated by McIntyre, who has established that, in the field studies, the mean deviation should range between ±1 [27] . In the x-axis of Figure 6, the statistical significance degree is also shown for the analyzed populations. In all cases, it rises above 99%, with the exception of type T3 in winter, which reaches only an 85% of confidence (p < 0.14).
Figure 6. Comparison between comfort vote and the average value of the measured operative temperature, as function of the year's seasons and the ventilation and acclimatization variants.
3.3. Thermal Preference Vote, PV
The information rendered by the PV (n = 528 questionnaires) is complementary to the one obtained through the CV, because it allows viewing defined the thermal acceptance profile [28] . The thermal acceptance range could be estimated from deductions on the comfort model proposed by Fanger [2] , who has defined that the users pleased by the thermal environment would vote CV = ±1, and those preferring a cooler space, or a warmer one than the one they are experiencing, would vote above +1 and below −1, respectively, over the 7 point ASHRAE scale. This criterion is adopted by the norm [1] and by other standards that base their selection upon this latter norm [15] and [29] .
In order to set a parallel comparison with Fanger’s research [2] , the thermal comfort/discomfort is expressed as a percentage value for the studied sample. Figure 7 shows that the percent spread of preference votes issued by users in the transient and summer periods and the vote of users that only during the measurements have shown thermal discomfort (PV ≠ 0), and that they would rather have a warmer setting (decreasing curve) or a cooler one (rising curve) than what currently was set. On the x-axis of Figure 7, the measured operative temperature are expressed every 2˚F (Fahrenheit) and in their Celsius equivalent. Figure 7 shows that the minimal percentage margin of users displeased with the thermal setting, either because of sensation cold or warm, is achieved at top = 23.3˚C. The intersecting point between both regression straight lines is a signal on the condition for maximum thermal comfort sensation.
Table 1 shows for each variant the values for preferred temperature, the number of buildings surveyed in summer and in the transient period. In summer, the preferred temperature is 1K (Kelvin) higher than in the transient period. In spaces of variant T3 minimal seasonal differences are observed (<± 0.5K). In summer, the desired temperature in spaces of variants T1 and T2 is 0.7 K higher than that of T3, which means
Figure 7. Percentage of dissatisfied users because of cooler/warmer thermal preference with respect to the operative temperature.
Table 1. Relationship between the mean values and the standard deviation of the preference temperature for the transient and summer periods.
that this is an adaptation sign of users of these variants types to the local climate. In the transient period, minimal differences are observed between the analyzed variants. For the analyzed population the statistical significance rises above 90%.
4. Discussion
4.1. Thermal Acceptance and Neutrality
In order to evaluate the thermal comfort, the measurement results are compared with those of the questionnaire by resorting to a minimal-square regression analysis. This allows defining an objective function and describing the behavior and interrelationship of variables. Several authors have expressed that this analysis is an appropriate method to design a comfort model [2] [22] [28] [30] [31] . From the contrasting analysis between operative temperature and the mean thermal sensation vote, it is possible to observe differences between the analyzed ventilation and acclimatization variants that deserve to be highlighted (see synthesis in Table 2).
In Figure 8, the slope b of the regression lines found for variants T1 = +0.52, T2 = +0.69 y T3 = +0.78 and their intersection with the values on the ASHRAE scale along the y-axis, allow finding operative temperature ranges bounded by “slightly cool” and “slightly warm” thermal sensation (CV = ±1). These ranges start between 21.4˚C and 22.0˚C and end between 24.6˚C and 25.3˚C, and they are an evidence on the thermal acceptance and adaptation degree of users. A temperature value does not have the same meaning for each of the analyzed variants. The larger amplitude of the acceptance of top is noted for spaces of T1 buildings, with a minimum of 21.4˚C and a maximum of 25.3˚C, which is a good signal that these users are more capable of adapting themselves to more ample thermal amplitudes.
It is worth noting that the differences between the gradients of each regression line are smaller than what was expected. Probably, the narrow range of top for variants T2 and T3 along the year decreases the significance of the obtained regression lines. Studies made in actual work spaces in hot climates show slopes b that range between +0.31 and +0.38 (Schiller et al., 1988). The difference with the slopes obtained here is indicative of an adaptation level of users to the Central-European climate, i.e., with smaller thermal amplitudes. The correlation r (Pearson coefficient), that is obtained from the pair values (top, CV) for variants T1 = +0.47, T2 = +0.48 and T3 = +0.54 in this work, highlights the importance of the influencing effect from surveying such a numerous
Figure 8. Linear regression model between the operative temperature and the mean thermal sensation vote as a function of the ventilation and acclimatization variants.
Table 2. Linear regression analysis between the measured operative temperature and the thermal sensation vote for the different variants on ventilation and acclimatization; mean values and standard deviation.
population of users responding to the questionnaire and who have different physical, physiological and psychological characteristics as regards temperature perception [32] . Experiences made in climatic chamber, such as those made by [2] , reach correlation coefficients r which range between +0.70 and +0.85, whereas in field studies, they fall between +0.30 and +0.55 [30] .
Conclusions in [4] , stated that the users of spaces with constant thermal conditions throughout the season experience a continuous adaptation process, regardless the external temperature. They eventually accept thermal conditions imposed upon them, even when the PMV “Predicted Mean Vote” (i.e., prediction vote on the mean thermal sensation vote) proposed by the norm [1] indicates that such thermal conditions are not good (compare to Figure 8 in [4] ). This allows justifying that the users of work spaces of variant T3 (air conditioning buildings) accept narrower ranges and smaller operative temperature deviations and that they prefer working with almost-constant thermal conditions (see Figure 8). It is worth saying that, the smaller the operative temperature range and the minimal the seasonal deviations are for this parameters (see Figure 6), the greater the users expectancies will be on thermal comfort (compare to [18] and [9] ).
The concept of thermal neutrality is useful to express the physical, physiological and psychological state with which the user experiences a pleasant thermal environment, i.e., s/he feels neither cold nor hot, and issues a CV = 0 (cero) on the 7-point ASHRAE scale. If it takes into account Griffith's statement indicating that when CV = 0, then top = tn (see [33] ), it is then possible to compute a neutrality temperature value (tn) for each study case. The values for operative temperature read on the intersection of the regression line with the y-axis = 0 in Figure 8 (thermal sensation vote, CV = 0) reach a reading of top = 23.2˚C for spaces of variant T1 and T2, and 23.3˚C in T3. The concept of neutrality is directly related with that of thermal preference. From comparing Figure 7 with Figure 8, it can be suggested the existence of an operative temperature range where the thermal dissatisfaction becomes minimal.
4.2. Variable Thermal Comfort Model
The development of a model for thermal comfort implies making a probability analysis between the thermal preference and the measured operative temperature readings and requires establishing a parallelism with Fanger’s studies (see [2] ). Figure 9 shows the regression line obtained by relating the thermal discomfort by preferring either cool or warmer condition respecting the measured operative temperature. Figure 9 shows the plots obtained by [2] in his experiments in a controlled climatic chamber. In order to make a comparison with Fanger’s model, it is plotted a regression resembling an inverted Gaussian distribution curve whose minimum value or the apex of the curve coincides with the minimum percentage of dissatisfied respecting the indoor thermal ambient, and with the neutral temperature value.
Figure 9. Percentage of dissatisfied because of cool/warm thermal sensation respecting the operative temperature [2] .
In Figure 10, the model developed here is superposed with Fanger’s curve (broken line curve). Fanger found the neutrality temperature to be 25.6˚C and a minimum percentage of dissatisfied of 5% [2] . In this work, it is found a neutrality temperature that is 2.3 K lower than Fanger’s and a minimum percentage of dissatisfied users of 7%, with top = 23.3˚C. In other studies of controlled climatic chambers, Mayer has defined that the minimum percentage of dissatisfied is not lower than 20% and he asserts this later on by stating that it does not go over 15% [8] . Huizenga study is based in gut number of research works, and he reaches a conclusion that the minimum percentage of dissatisfied users could rise even over 40% [34] .
In Figure 10 can be noted that the dissatisfaction rating increases as the operative temperature changes either higher or lower than 23.3˚C. This allows defining thermal acceptance ranges. When observing Figure 10, 10% of dissatisfied users lie within a top range of 23.3˚C ± 1.1˚C, and it reaches 20% as long as the operative temperature does not rise over 25.5˚C or descend below 21.5˚C. About 35% of dissatisfied users lie in the range 23.3˚C ± 3˚C.
Equation (1) responds to the probability analysis developed in this work and represents the function of the non-linear regression curve shown in Figure 10. This equation allows computing a variable thermal comfort. The prediction model proposed in this work, allows introducing two local variables that define the thermal comfort condition: variable I, which is the computed neutrality temperature when considering the comfort vote of users, and variable 2, which is the value of the measured operative temperature. In this way, it is possible to consider the influencing factors on the degree of thermal adaptation of users, altogether with the seasonal climatic differences, the geographical, cultural and other factors. This integration, leads to a better optimization of climate management in buildings in operation, with variations in the ventilation and acclimatization systems.
Figure 10. Percentage of dissatisfied as a function of the measured temperature.
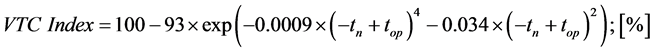 (1)
(1)
 = temperature of neutrality (variable 1),
= temperature of neutrality (variable 1),

5. Conclusions
The evaluation of thermal comfort shows clear differences arising in thermal acceptance expressed by user of different variant spaces as regards ventilation and acclimatization strategies.
Although Fanger warns on the possibility of users’ thermal adaptation and the influence of climatic, geographical, cultural and other factors on thermal comfort, the comfort formula that he has developed does not allow those kinds of variations. The study presented allows the conclusion that the comfort model has to introduce the variables pertaining to the local surroundings.
The slope b of the regression analysis is an indicator of the adaptation of users to the local climate. The users of spaces having natural ventilation experience a more frequent contact with the outdoor surroundings and, therefore, are more tolerant to wider operative temperature ranges and swings, whereas the users of acclimatized spaces experience just minimal temperature variations and, consequently, are more sensitive to temperature changes. The thermal perception of users of variant T3 is one and a half (1.5) more sensitive than the users of variant T1. In spaces of variant T2, intermediate situation is noted, where the users are approximately 1.2 times more sensitive than those of variant T1.
The different adaptation levels expressed by users can not be evaluated under a single criterion; actually, they rather constitute a potential challenge for reaching at a more efficient operative level in buildings with different ventilation and acclimatization systems.
On the basis of the model developed in this work, it is worth noting the importance of surveying the comfort vote, and the need that both the questionnaire and measurement tasks be made simultaneously, so as to be able to compute the neutrality temperature and to describe the thermal comfort zone. A similar result is obtained for the preference temperature which, in addition, is useful to show the thermal discomfort in percentage values.
Equation (1) and Figure 10 allow knowing the thermal comfort of a group of users, incorporating top and tn as variables. This allows expounding the user response on thermal comfort of real spaces, and developing the strategies for a more convenient energy optimization of buildings.
Cite this paper
Kuchen, E. (2016) Variable Thermal Comfort Index for Indoor Work Space in Office Buildings: A Study in Germany. Open Journal of Civil Engineering, 6, 670-684. http://dx.doi.org/10.4236/ojce.2016.64054
References
- 1. ISO 7730 (2005) Ergonomics of the Thermal Environment. Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria.
- 2. Fanger, P.O. (1970) Thermal Comfort. Technical University of Denmark, Laboratory of Heating and Air Conditioning, Danish Technical Press, Copenhagen.
- 3. Kuchen, E. (2008) Spot-Monitoring zum thermischen Komfort in Bürogebäude. PhD Thesis, Dissertation, Technische Universität, Braunschweig. Der Andere Verlag, Tönning, Germany.
- 4. Kuchen, E and Fisch, M.N. (2009) Spot Monitoring—Thermal Comfort Evaluation in 25 Office Buildings in Winter. Building and Environment, 44, 839-847.
http://dx.doi.org/10.1016/j.buildenv.2008.06.023 - 5. Bedford, T. (1950) Environmental Warmth and Human Comfort. British Journal and Applied Physics, 1, 33-38.
http://dx.doi.org/10.1088/0508-3443/1/2/301 - 6. Frank, W. (1975) Raumklima und Thermische Behaglichkeit. Institut für Bauphysik der Fraunhofer-Gesellschaft zur Förderung der angewandten Forschung e. V. mit 21 Bildern und 12 Tabellen. Wilhelm Ernst & Sohn KG., Germany.
- 7. Auliciems, A. (1969) Effects of Weather on Indoor Thermal Comfort. International Journal of Biometeorology, 13, 147-162.
http://dx.doi.org/10.1007/BF01552736 - 8. Mayer, E. (1998) Ist die bisherige Zuordnung von PMV und PPD noch richtig? Klimatechnik/Behaglichkeit. Ki Luft-und Kältetechnik, 54, 575-577.
- 9. Hellwig, R.T. (2005) Thermische Behaglichkeit. Unterschiede zwischen frei-und mechanischen belüfteten Büro-gebäuden aus Nutzersicht. PhD Thesis Dissertation, Technische Universität, München.
- 10. Nicol, J.F. and Humphreys, M.A. (2002) Adaptive Thermal Comfort and Sustainable Thermal Standards for Buildings. Oxford Centre for Sustainable Development, School of Architecture, Oxford Brookes University, Oxford.
- 11. De Dear, R. (2004) Thermal Comfort in Practice. Division of Environmental and Life Sciences, Macquarie University, Australia. Indoor Air, 14, 32-39.
http://dx.doi.org/10.1111/j.1600-0668.2004.00270.x - 12. Raue, A.K., Boestra A.C., van der Linden, A.C. and Kurvers, S.R. (2004) NATVENT Buildings versus HVAC Buildings. A New Dutch Thermal Comfort Guideline. 25th Air Infiltration and Ventilation Centre Conference, Prague, 15-17 September 2004.
- 13. Hellwig, R.T. and Bischof, W. (2006) Gültigkeit Therzmischer Behaglichkeitsmodelle. Bauphysik, 28, 131-136.
http://dx.doi.org/10.1002/bapi.200610013 - 14. Boestra, A.C. (2006) The Adaptive Thermal Comfort Criterion in the New EPBD IEQ Standard. BBA Indoor Environmental Consultancy, the Netherlands.
http://nceub.org.uk/dokuwiki/lib/exe/fetch.php?media=nceub:uploads:members:w2006:session1:w2006_boerstra.pdf - 15. ASHRAE 55 (2004) Thermal Environmental Conditions for Human Occupancy. (Supersedes ANSI/ASHRAE Standard 55 (1992)).
- 16. Nicol, J.F. and Humphreys, M.A. (2005) Maximum Temperatures in Buildings to Avoid Heat Discomfort. International Conference of Passive and Low Energy Cooling for the Built Environment, Santorini, 19-21 May 2005.
- 17. Fisch, M.N., Plesser, S., and Bremer, C. (2007) EVA—Evaluierung von Energiekonzepten für Bürogebäude. Bericht zur Grobanalyse, BMWA.
- 18. De Dear, R., Brager, G.S. and Cooper, D. (1997) Developing an Adaptive Model of Thermal Comfort and Preference. ASHRAE RP-884, Macquarie University, Sydney, Australia and Centre for Environmental Design Research, University of California, Berkley.
- 19. Raue, A.K., Kurvers, S.R., van der Linden, A.C., Boestra, A.C. and Plokker, W. (2006) Dutch Thermal Comfort Guidelines. From Weighted Temperature Exceeding Hours towards Adaptive Temperature Limits, The Netherlands.
- 20. Gonzalo, G.E., Nota, V.M., Hernández, S.P., Martínez, C.F. and Ledesma, S.L. (2007) Diseño Bioclimático de Oficinas. Instituto de Acondicionamiento Ambiental, Tucumán, Argentina, 285.
- 21. DIN EN ISO 7726 (2002) Umgebunsklima. Instrumente zur Messung physikalischer Gröbetaen, Deutsche Fassung.
- 22. Schiller, G.E., Arens, E.A., Bauman, P.E., Benton, C., Fountain, M. and Doherty, T. (1988) A Field Study of Thermal Environments and Comfort in Office Buildings. Centre for the Built Environment, University of California, No. 3164 (RP-462), Berkley.
- 23. McCartney, K.J. and Nicol, J.F. (2002) Developing an Adaptive Control Algorithm for Europe: Results of the SCATs Project. Oxford Centre for Sustainable Development, Oxford Brookes University, Oxford.
- 24. Cena, K. and de Dear, R. (1998) Field Study of Occupant Comfort and Office Thermal Environments in a Hot-Arid Climate. Final Report ASHRAE, RP-921, Institute for Environmental Science, Murdoch University, Perth.
- 25. EN ISO 10551 (2002) Ergonomie des Umgebungsklimas. Beurteilung des Einflusses des Umgebungsklima unter Anwendung subjektiver Bewertungsskalen. Deutsche Fassung (ISO 19551 (1995)).
- 26. Auliciems, A. and de Dear, R. (1986) Air Conditioning in a Tropical Climate: Impacts upon European Residents in Darwin, Australia. International Journal of Biometerology, 30, 259- 282.
http://dx.doi.org/10.1007/BF02189471 - 27. McIntyre, D.A. (1978) Three Approaches to Thermal Comfort. ASHRAE Transactions, 84, 101-109.
- 28. De Dear, R. and Brager, G.S. (2001) The Adaptive Model of Thermal Comfort and Energy Conservation in the Built Environment. International Journal of Biometerology, 45, 100- 108.
http://dx.doi.org/10.1007/s004840100093 - 29. ISSO 74 (2004) Thermische Behaaglijkeid. New Dutch Thermal Comfort Guideline. Publication 74, Rotterdam, Holland.
- 30. Auliciems, A. (1981) Towards a Psycho-Physiological Model of Thermal Perception. International Journal of Biometerology, 25, 109-122.
http://dx.doi.org/10.1007/BF02184458 - 31. Nicol, J.F. and Raja, I.A. (1997) Indoor Thermal Comfort: The Pakistan Study. Energy for Sustainable Development, 3, 50-60.
http://dx.doi.org/10.1016/S0973-0826(08)60213-6 - 32. Ye, X.J., Zhou, Z.P., Lian, Z.W., Liu, H.M., Li, C.Z. and Liu, Y.M. (2006) Field Study of a Thermal Environmental and Adaptive Model in Shanghai. Indoor Air, 16, 320-326.
http://dx.doi.org/10.1111/j.1600-0668.2006.00434.x - 33. Griffiths, I. (1990) Thermal Comfort Studies in Buildings with Passive Solar Features. Field Studies. Report to the Commission of the European Community, ENS35 090 UK.
- 34. Huizenga, C., Abbaszadeh, S., Zagreus, L. and Arens, E. (2006) Air Quality and Thermal Comfort in Office Buildings: Results of a Large Indoor Environmental Quality Survey. Proceedings of Healthy Buildings, 3, 393-397.











