Open Journal of Civil Engineering
Vol.05 No.02(2015), Article ID:57322,6 pages
10.4236/ojce.2015.52026
Analysis of the Probability Model of Wind Load on the Offshore Wind Turbine
Bowen Jiang1, Mingjie Zhao1, Pan Liu1, Ziyuan Tang2
1School of River and Ocean Engineering, Chongqing Jiaotong University, Chongqing, China
2Department of Mathematics, Nanjing University, Nanjing, China
Email: jbw1991222@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 May 2015; accepted 19 June 2015; published 23 June 2015
ABSTRACT
According to the actual measurement data, probability models of horizontal wind load were obtained based on wind velocity statistic and power spectral density function of fluctuating wind velocity through stochastic sampling and using spectrum analysis method. Through the comparison of two models, probability models of horizontal wind load based on probability models of fluctuating wind velocity were obtained by revising the mean and variance of fluctuating wind velocity. Results show that the variance takes lower value when the power spectral density function of fluctuating wind velocity is used to obtain the probability model of horizontal wind load. The quadratic term of fluctuating wind velocity takes a small contribution value in total wind load with almost no contribution to the model of horizontal wind load. It is convenient for practical engineering to obtain the models of horizontal wind load by using probability models of fluctuating wind velocity.
Keywords:
The Offshore Wind Turbine, Spectrum Analysis, Non-Central Chi-Square Distribution, Probability Density Function

1. Introduction
At present, as a new and efficient renewable energy, wind power has caused widespread concern in the industry. Due to the complex environmental loads and variable factors, offshore wind turbine works are still in the offshore range. Therefore, the reliability of offshore wind turbine under the environment load is not only an important basis for the structure design and construction of offshore wind turbine, but also the foundation of the wind turbine works in the deep sea area.
Wind load, as the main load of the offshore wind turbine structure, is the crucial factor of the offshore wind turbine reliability [1] . Meanwhile, because of its characteristics of indeterminacy, pulsation and changing along the elevation, the effect of wind load is difficult to combine linearly with others [2] . Therefore, the analysis of probability model of wind load on offshore wind turbine is of great significance. Over a long period of time, the probability model of horizontal wind load has been established and studied based on wind velocity statistic. However, due to the high cost and regional dependence of statistical information, a more practical probability model of horizontal wind load needs to be established based on characteristics of wind load.
2. Theoretical Analysis of Wind Load
The wind force on structure is related to wind velocity, its calculation is shown as follows [3] .
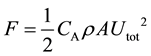 (1)
(1)
where:
F = wind force (kN).
A = area that wind force covers (m2).
CA = shape coefficient of building, which equals the ratio of actural wind pressure to wind pressure from velocity calculation [4] .
ρ = density of air (kg/m3).
Utot = horizontal wind velocity (m/s).
The characteristic of wind velocity is fluctuant. The value of wind velocity at a fixed height fluctuates around a certain value, which is called static wind velocity. The random fluctuation value of wind velocity is called fluctuating wind velocity. Take horizontal component of wind velocity (horizontal wind velocity) as an example, its formula is shown in as follows.
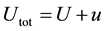 (2)
(2)
where:
Utot = horizontal wind velocity (m/s).
U = static wind velocity (in horizontal direction) (m/s).
u = fluctuating wind velocity (in horizontal direction) (m/s).
Generally, static wind velocity occupies a large proportion in total wind velocity. Logarithmic law and exponential law are two common laws of wind velocity profile with respect to height. The exponential wind velocity profile is simpler in calculation while the logarithmic wind velocity profile is thought to be a more practical profile which is shown as following equation [5] .
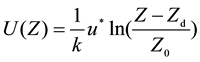 (3)
(3)
where
U(Z) = wind velocity with respect to height (m/s).
Z = height (m).
k = Von Karman’s coefficient.
u* = velocity of flow hear stress (m/s).
Zd = height of zero plane (m); Z0 = roughness length (m).
The calculation formula of wind load is easy to be introduced by Equation (1) and Equation (2), shown as following equation [6] .
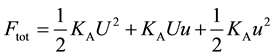 (4)
(4)
where:
Ftot = horizontal wind load (N).
U = static wind velocity (in horizontal direction) (m/s).
u = fluctuating wind velocity (in horizontal direction) (m/s).
KA = specified coefficient, KA = CAρA.
3. Analysis of Wind Load Probability Model
3.1. Horizontal Wind load Based on Wind Velocity Statistic
According to the data [7] , the wind velocity at the height of 70 meters obeys the law of Gaussian distribution. The mean value of wind velocity at the height of 70 meters is approximately 7.12 (m/s), the variance is 8.88 (m2/s2). It can be considered that the horizontal wind velocities at different heights all obey the law of Gaussian distribution. The mean values and the variances could be calculated on the basis of the mean value and variance of wind velocity at the height of 70 meters. The total horizontal wind load equals the sum of horizontal wind load at all heights, so the distribution law of total horizontal wind load obeys the law of Non-Central Chi-Square distribution. The probability density function of standard Non-Central Chi-Square distribution is shown as following equations.
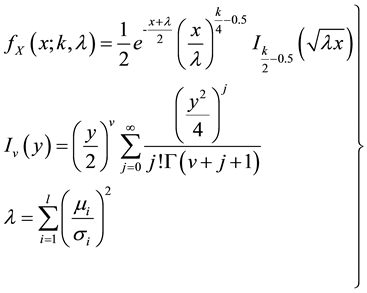 (5)
(5)
where:
fX(x; k, λ) = the probability density function of standard Non-Central Chi-Square distribution.
k = the number of degrees of freedom.
λ = the noncentrality parameter.
μi = the mean value of each Gaussian stochastic variable.
σi = the variance of each Gaussian stochastic variable.
The height of wind turbine is 70 meters, the height of zero plane is 2 meters, the roughness length is 0.01 meters. At the interval of 1 meter, the wind velocity of the midpoints represents the velocity of the whole interval. The mean values and variances of the horizontal velocities along the height were calculated as shown in Figure 1.
Figure 1. The mean values and variances of the horizontal velocities along the height.
The parameters of standard Non-Central Chi-Square distribution which total horizontal wind load obeys were calculated as shown in Table 1.
3.2. Horizontal wind Load Based on Power Spectral Density Function of Fluctuating Wind Velocity
Fluctuating wind can be approximated as stationary stochastic process, the power spectral density function of fluctuating wind velocity at height of Z is shown as following equation. The mean value of fluctuating wind velocity is zero. The variance could be obtained by calculating the integral of the power spectral density function of fluctuating wind velocity with respect to frequency.
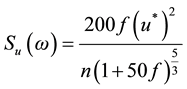 (6)
(6)
where:
Su(n) = the power spectral density function of fluctuating wind velocity at height of Z.
n = frequency of fluctuating wind (s−1).
f = the Similarity coordinate, f = nZ/U(Z).
U(Z) = the static wind velocity (in horizontal direction) at height of Z (m/s).
When taking the static wind velocity as a constant, according to Equation (4), the quadratic term of fluctuating wind velocity obeys the law of Non-Central Chi-Square distribution, the first power term of fluctuating wind velocity obeys the law of Gaussian distribution. There’s one point which needs attention: the noncentrality parameter of Non-Central Chi-Square distribution can’t be defined as zero, meanwhile, the mean value of fluctuating wind velocity is defined exactly as zero. Therefore, it is considered that fluctuating wind velocity fluctuates around zero in a small range (±δ). The parameters of total horizontal wind load (when taking the static wind velocity as a constant) were calculated as shown in Table 2.
3.3. Comparison and Revise
The probability density functions of horizontal wind load based on wind velocity statistic and the power spectral density function of fluctuating wind velocity were obtained and shown in Figure 2.
From Figure 2, the range of wind load values is narrower and the mean value is higher when using the power spectral density function of fluctuating wind velocity to determine the horizontal wind load. This is caused by the superposition of basis value (constant term) during calculation of the horizontal wind load (the mean value of horizontal wind load based on wind velocity statistic is lower without the superposition of basis value). Therefore, the failure probability is higher and considered to be conservative. In order to study the comparison of contribution in total wind load between the first power term of fluctuating wind velocity and the quadratic term of fluctuating wind velocity, the values of the two terms during the simulation process are stochastic sampled and shown in Figure 3.
From Figure 3, the values of the first power term are much higher than that of the quadratic term. Therefore, the quadratic term could be approximately neglected. On account of the inappropriate variance of the fluctuating
Table 1. The parameters of standard non-central Chi-Square distribution which total horizontal wind load obeys.
Table 2. The parameters of total horizontal wind load.
Figure 2. The probability density functions of horizontal wind load based on wind velocity statistic and power spectral density function of fluctuating wind velocity.
Figure 3. The value of the two terms during the simulation process.
wind velocity (obtained by calculating the integral of the power spectral density function of fluctuating wind velocity with respect to frequency), the probability density functions of horizontal wind load based on power spectral density function of fluctuating wind velocity is quite different from that based on wind velocity statistic. Therefore, it is necessary to revise the probability model of horizontal wind load based on power spectral density function of fluctuating wind velocity. To be commensurate with the probability model of horizontal wind load based on wind velocity statistic, the appropriate variance of the first power term of fluctuating wind velocity is supposed to be 9 × 104 (N2), the mean value of the first power term of fluctuating wind velocity is supposed to be 3200 (N). The probability density functions of horizontal wind load based on wind velocity statistic and the probability density functions of horizontal wind load based on the probability models of fluctuating wind velocity are shown in Figure 4. Through revising, the variances of the horizontal velocities along the height were calculated as shown in Figure 5. The percentage of error of the two probability models during the simulation process are stochastic sampled and shown in Figure 6.
Figure 4. The probability density functions of horizontal wind load based on wind velocity statistic and the probability models of fluctuating wind velocity.
Figure 5. The variances of the horizontal velocities along the height.
Figure 6. The percentage of error of the two probability models during the simulation process.
In practical engineering, the fluctuating wind velocity probability distribution model could be deduced as soon as the annual mean wind velocity of a certain height is determined. Then, the probability models of total wind load are obtained.
4. Conclusions
Results show that the reliability of probability forecast is proved to be valid and conservative when the probability models of fluctuating wind velocity are used to obtain the probability model of horizontal wind load. It is convenient for practical engineering to obtain the models of horizontal wind load by using probability models of fluctuating wind velocity, when the comprehensive and numerous measured data are difficult to obtain.
In the analysis of probability model of wind load, established model of fluctuating wind velocity is adopted, which needs to be improved and validated comprehensively on account of randomness and unpredictability of fluctuating wind. In the diverse offshore environment, many factors (such as the wave and current) of the wind load are connotative associated and need to be studied more systematically. Further researches on above issues will become the foundation and direction of establishing more accurate probability models of wind load.
Acknowledgements
This project is supported by National Natural Science Foundation of Chongqing (CSTC2013JJB30002) and Research Fund for the Doctoral Program of Higher Education of China (20125522110004).
References
- Lv, F.Y., Yang S.C., Zhan, J.M, Li, Q.X., Xv, W., Tang, J., et al. (2008) Numerical Wind-Tunnel Simulation of Wind Pressure on High-Rise Buildings. Acta Scientiarum Naturalium Universitatis Sunyatseni (Natural Sciences), 47, 118- 121.
- Jiang, Y.B. and Yang W.J. (2012) Research on Values of Load Partial Factors with Large Ratios of Variable Load Effects. Journal of Building Structures, 33, 130-135.
- He, D.X. (2006) Wind Engineering and Industrial Aerodynamics. National Defence Industrial Press, Beijing.
- JTG/T-D60-01-2004 (2004) Wind-Resistant Design Specification for Highway Bridges (in Chinese).
- Chen, Z.Q. (2005) Bridge Wind Engineering. 1st Edition, China Communications Press, Beijing.
- Claes, D. and Svend, O.H. (1996) Wind Loads on Structures. 1st Edition, John Wiley and Sons, Ltd. Press, New York.
- Zhang, W.M. (2009) The Overall Planning Report of Offshore Wind Farm and Intertidal Zone in Rudong County (in China). HydroChina Huadong Engineering Corporation, Hangzhou.








