Journal of Applied Mathematics and Physics
Vol.04 No.08(2016), Article ID:70197,9 pages
10.4236/jamp.2016.48174
Bending and Vibrations of a Thick Plate with Consideration of Bimoments
Мakhamatali K. Usarov, Davronbek М. Usarov, Gayratjon T. Ayubov
Institute of Seismic Stability of Structures of the Academy of Sciences of the Republic of Uzbekistan, Tashkent, Uzbekistan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 July 2016; accepted 27 August 2016; published 30 August 2016
ABSTRACT
The paper is dedicated to the development of the theory of orthotropic thick plates with consideration of internal forces, moments and bimoments. The equations of motion of a plate are described by two systems of six equations. New equations of motion of the plate and the boundary conditions relative to displacements, forces, moments, and bimoments are given. As an example, the problems of free and forced oscillations of a thick plate are considered under the effect of sinusoidal periodic load. The problem is solved by Finite Difference Method. Eigenfrequencies of the plate are determined, numeric maximum values of displacements, forces and moments of the plate are obtained depending on the frequency of external force. It is shown that when the value of the frequency of external effect approaches the eigenfrequency, there occurs an increase in displacement, force and moment values; that testifies a gradual transition of the motion of plate points into the resonant mode.
Keywords:
Plate, Orthotropic, Isotropic, Displacement, Stress, Moment, Bimoment, Bending, Vibrations

1. Introduction
Theory of plates and shells has a special place in design of structural elements. Specified theories of plates are built by many authors. All existing specified theories of plates are developed on the basis of a number of simplifying hypotheses. An overview of the main statements and common methods of constructing an improved theory of plates and shells can be found in the works of S. A. Ambartsumyan [1] , K. Z. Galimov [2] , Sh. K. Galimov [3] , Kh. M. Mushtari [4] and others. Static problem of the bending of a thick isotropic plate in three- dimensional theory of elasticity is considered by B.F. Vlasov in [5] , which gives an exact analytical solution in trigonometric series. Monograph by E.N. Baida [6] is devoted to solving the problem of bending of orthotropic plates in trigonometric series. Numerical results of displacements and stresses are obtained.
The authors in [7] - [10] deal with dynamic problems of plates with anisotropic properties. Karamooz Ravari M.R., Forouzan M.R. [7] have studied the problems of plates oscillations. Frequency equations of orthotropic circular ring plate were obtained for general boundary conditions in oscillation plane. In [8] the solution of transition oscillations of rectangular viscous-elastic orthotropic plate are given for concrete strain models according to Flugge and Timoshenko-Mindlin’s theories. The paper [9] is devoted to analytical solution of the problem of forced steady-state vibrations of orthotropic plate. By the method of superposition the problem is reduced to a quasi-regular infinite system of linear equations. In [10] an analytical method of solution of spatial problem of bending of orthotropic elastic plates subjected to external loads on upper and lower edges is developed. In [11] a problem is considered of a bending of orthotropic rectangular plate laying on two-parameter elastic foundation. Research in the field of thick plates has shown that in the case of spatial deformation of a plate along its thickness there occurs the nonlinear laws of displacements distribution and the hypothesis of plane sections is violated. In the cross-sections of the plate except for the tensile and shear forces, bending and torsional moments, there appear the additional force factors, the so-called bimoments. The author of the article addresses the problem of bending and vibrations of thick plates based on bimoment theory of plates [12] - [15] , built as a part of three-dimensional theory of elasticity, using the method of displacements decomposition in one of the spatial coordinates in Maclaurin infinite series.
This paper gives a brief description of the technique of constructing a theory of plates with consideration of bimoments generated due to displacements distribution of cross-section points by a non-linear law. Here the equations of bimoments are built with the equation of three-dimensional dynamic theory of elasticity, described on face surfaces of the plate. The bimoments are introduced in stress dimensions and are characterized by the intensity of generated bimoments. We would use the designations and determinant correlations of forces, moments, bimoments and equations of motion relative to these force factors.
Unlike bimoment theory in [14] and [15] , here the bimoment equations are built with the equation of three- dimensional dynamic theory of elasticity, described on face surfaces of the plate. Bimoments are introduced in stress dimensions, and they characterize the intensity of generated bimoments.
Determinant relationships of forces, moments, bimoments and equations of motion relative to these force factors are given.
2. Statement of the Problem
Consider an orthotropic thick plate of constant thickness 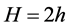 and dimensions
and dimensions 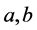 in plane. Introduce the designations:
in plane. Introduce the designations: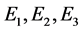 ―elasticity moduli;
―elasticity moduli;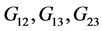 ―shear moduli;
―shear moduli;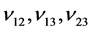 ―Poisson ratio of plate material.
―Poisson ratio of plate material.
When building an equation of motion the plate is considered as a three-dimensional body and all components of stress and strain tensors: 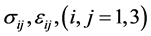 are taken into consideration. The components of displacement vector are the functions of three spatial coordinates and time
are taken into consideration. The components of displacement vector are the functions of three spatial coordinates and time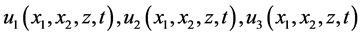 .
.
The components of strain tensor 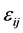 are determined from Cauchy relation as:
are determined from Cauchy relation as:
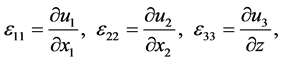 (1.а)
(1.а)
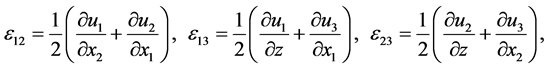 (1.b)
(1.b)
For orthotropic plate, the Hooke’ law, in a general case, is written as:
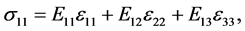 (2.a)
(2.a)
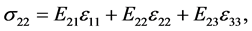 (2.b)
(2.b)
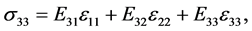 (2.c)
(2.c)
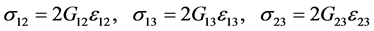 (2.d)
(2.d)
where 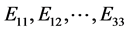 are the elastic constants, determined through Poisson ratio and the moduli of elasticity in the form [14] [15] .
are the elastic constants, determined through Poisson ratio and the moduli of elasticity in the form [14] [15] .
As an equation of motion of a plate we would use three-dimensional equations of dynamic theory of elasticity:



where 
Boundary conditions on lower and upper face surfaces of the plate 



Here 




3. Method of Solution
The methods of building the bimoment theory of plates are based on Cauchy relation (1), generalized Hooke’s law (2), three-dimensional equations of the theory of elasticity (3), boundary conditions on face surfaces (4). A proposed bimoment theory of plates is also described by two non-connected problems, each of which is formulated on the basis of six two-dimensional equations of motion with corresponding boundary conditions.
The components of displacement vector are expanded into Maclaurin infinite series in the form:


Here 


The displacements in stresses in upper 



The first problem of bimoment theory describes tension-compression and transverse reduction of the plate, and the second one―the bending and transverse shear of the plate. Determinant relationships and corresponding equations of motion of the plate in the first and second problems are briefly described below.
The first problem is described by the forces and bimoments with six generalized functions


Introduce the external loads for the first problem

The expressions of longitudinal and tangential forces are written as [12] - [15] :



The intensities of the bimoments 


The intensity of the bimoment 


The equations of motion relative to longitudinal and tangential forces and bimoments from tangential and normal stresses have the form [12] - [15] :


Note, that the expressions of force factors (9), (10), and hence, the equations of motion of the system (11), (12) is rigorously built. This system consists of three equations relative to six unknown functions

The second problem of bimoment theory consists of the equations for bending moments, torsional moments, shear forces relative to six kinematic functions


Introduce the generalized external loads for the second problem

Bending, torsional moments and shear forces, which are rigorously built, have the form [12] - [15] :




The system of equations of motion of the second problem consists of two equations relative to bending, torsional moments and one equation relative to shear force and it is written in the form [12] - [15] :


Note, that the expressions of forces and moments (16), hence, the equations of motion of the system (17), (18) are rigorously built. Similar to the first problem, here three equations are missed. The system of equations of motion (17), (18) consists of three equations relative to six unknown functions





To complete the systems (11), (12) and (17) and (18) it is necessary to build two more systems, with three equations in each. Write down three equations of motion of the theory of elasticity (3) on face surfaces of the plate 





Here the intensities of the bimoments





The second system of equations obtained from the equations of the theory of elasticity (3) is written in the form:


Here 


The intensities of the bimoments


The intensities of the bimoments 




Here
The expressions of the intensities of the bimoments 






The expressions of the intensities of the bimoments 






Write down the formulae to determine the displacements on the face surfaces of the plate 


Formulae for stresses on the face surfaces of the plate 


Maximum values of displacements and stresses of the plate are reached on the face surfaces of the plate and are determined by the solutions of the first and second problems by the formulae (33) and (34).
Note, that the expressions of intensities of the bimoments (10), (27), (28), (29), (30), (31) and (32) are built for the first time and are new in the theory of plates.
Consider the boundary conditions of a discussed problem for the thick plates.
1) On the border of the plate the displacements are zero. On the edges of the plate 



2) On the border 


3) On the border 


Boundary conditions on the border 
When studying the problem of transverse bending and shear it is enough to consider only the second problem with the equations of motion (17), (18), (23), (24) and boundary conditions (35)-(40).
4. Solution of Tests Problem
As an example, consider the forced harmonic vibrations of a cantilever rectangular plate fixed on both ends under the effect of harmonic periodic external load:

where 

Substituting (41) into (8) and (15) determine the load terms of the equation of motion. For a plate fixed on both ends the boundary conditions are written in the form (35) and (36).
5. Numeric Results
First determine eigenfrequencies of the plate. After dividing the variables by spatial coordinates and time, the problem is solved by Finite Difference Method. The step in spatial coordinates is

For square plates with dimensions 





Table 1 shows the results obtained for the displacements, moments and forces in fixed square plates


of external effect 

Table 2 and Table 3 show numeric values of displacements, moments and forces, calculated for the fixed square plates with dimensions 


Calculations show that when the value of the frequency of external effect 
Table 1. Displacements, forces and moments at
Table 2. Displacements, forces and moments at
Table 3. Displacements, forces and moments at
Calculations show that the equations of motion of a plate (23) may be substituted by kinematic conditions relative to tangential stresses:

Kinematic equations serve to determine the generalized displacements
The equations (26) are determined by the solution of the system of linear algebraic equations relative to coefficients of the series (5)


6. Conclusion
Based on these studies, we would note that using the method of expansion in a series as part of three-dimen- sional dynamic theory of elasticity, a two-dimensional bimoment theory of orthotropic thick plates was developed and the equations of motion of the plate relative tot forces, moments and bimoments were built. It is shown that the problem in the general case is reduced to the definition of twelve unknown functions of two spatial coordinates and time. New expressions to determine the forces, moments and bimoments of the plates were built, as well as the methods for solving the problems of free and forced vibrations of plates based on Finite Difference Method.
Cite this paper
Мakhamatali K. Usarov,Davronbek М. Usarov,Gayratjon T. Ayubov, (2016) Bending and Vibrations of a Thick Plate with Consideration of Bimoments. Journal of Applied Mathematics and Physics,04,1643-1651. doi: 10.4236/jamp.2016.48174
References
- 1. Ambartsumyan, S.A. (1987) Theory of Anisotropic Plates. Nauka, Ch. Ed. Sci. Lit., Moscow, 360 p.
- 2. Galimov, K.Z. (1977) Theory of Shells with Account of Transverse Shear. Ed. Kazan University, Kazan, 212 p.
- 3. Galimov, Sh.K. (1976) Specified Theory of Calculation of Orthotropic Rectangular Plate under Lateral Load. Investigations in Theory of Plates and Shells, Sat. articles, Kazan, Vol. XII, 78-84.
- 4. Mushtari, Kh.M. (1990) Nonlinear Theory of Shells. Nauka, Moscow, 223 p.
- 5. Vlasov, B.F. (1952) On a Case of Bending of a Rectangular Thick Plate. Vestnik MGU. Mechanics, Mathematics, Astronomy and Chemistry, No. 2, 25-34.
- 6. Baida, E.N. (1983) Some Spatial Problems of Elasticity. Leningrad University, Leningrad, 232 p.
- 7. Karamooz Ravari, M.R. and Forouzan, M.R. (2011) Frequency Equations for the In-Plane Vibration of Orthotropic Circular Annular Plate. Archive of Applied Mechanics, 81, 1307-1322.
- 8. Soukup, J., Vales, F., Volek, J. and Skocilas, J. (2011) Transient Vibration of thin Viscoelastic Orthotropic Plates. Acta Mechanica Sinica, 27, 98-107.
- 9. Papkov, S.О. (2013) Steady-State Forced Vibrations of a Rectangular Orthotropic Plate. Journal of Mathematical Sciences, 192, 691-702.
- 10. Chang, H.-H. and Tarn, J.-Q. (2012) Three-Dimensional Elasticity Solutions for Rectangular Orthotropic Plates. Journal of Elasticity, 108, 49-66.
- 11. Zenkour, A.M., Allam, M.N.M., Shaker, M.O. and Radwan, A.F. (2011) On the Simple and Mixed First-Order Theories for Plates Resting on Elastic Foundations. Acta Mechanica, 220, 33-46.
- 12. Usarov, M.K. (2014) Calculation of Orthotropic Plates Based on the Theory of Bimoments. Uzbek Journal Problems of Mechanics, Tashkent, No. 3-4, 37-41.
- 13. Usarov, M.K. (2014) Bimoment Theory of Bending and Vibrations of Orthotropic Thick Plates. Vestnik NUU, No. 2/1, 127-132.
- 14. Usarov, M.K. (2015) Bending of Orthotropic Plates with Consideration of Bimoments. St. Petersburg, Civil Engineering Journal, 1, 80-90.
- 15. Usarov, M.K. (2015) On Solution of the Problem of Bending of Orthotropic Plates on the Basis of Bimoment Theory. Open Journal of Applied Sciences, 5, 212-219.
http://dx.doi.org/10.4236/ojapps.2015.55021



