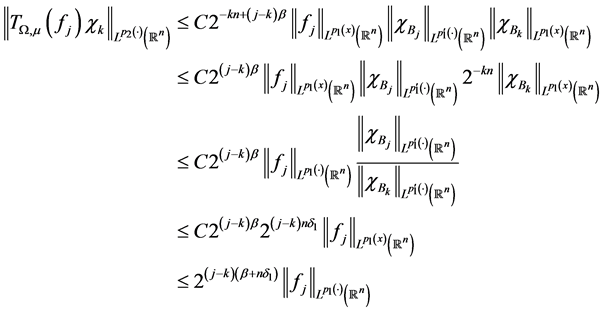Journal of Applied Mathematics and Physics
Vol.04 No.04(2016), Article ID:66110,9 pages
10.4236/jamp.2016.44089
The Boundedness of Fractional Integral with Variable Kernel on Variable Exponent Herz-Morrey Spaces
Afif Abdalmonem1,2*, Omer Abdalrhman1,3, Shuangping Tao1
1College of Mathematics and Statistics, Northwest Normal University, Lanzhou, China
2Faculty of Science, University of Dalanj, Dalanj, Sudan
3College of Education, Shendi University, Shendi, Sudan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 March 2016; accepted 24 April 2016; published 28 April 2016
ABSTRACT
In this paper, we study the boundedness of the fractional integral with variable kernel. Under some assumptions, we prove that such kind of operators is bounded from the variable exponent Herz-Morrey spaces to the variable exponent Herz-Morrey spaces.
Keywords:
Fractional Integral, Variable Kernel, Variable Exponent, Herz-Morrey Spaces

1. Introduction
Let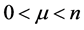 ,
,  is homogenous of degree zero on
is homogenous of degree zero on ,
,  denotes the unit sphere in
denotes the unit sphere in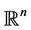 . If
. If
i) For any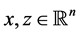 , one has
, one has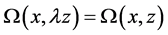 ;
;
ii) 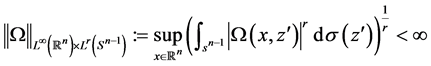
The fractional integral operator with variable kernel 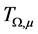 is defined by
is defined by
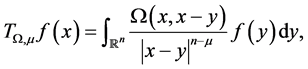
When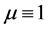 , the above integral takes the Cauchy principal value. At this time
, the above integral takes the Cauchy principal value. At this time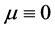 ,
, 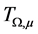 is much more close related to the elliptic partial equations of the second order with variable coefficients. Now we need the further assumption for
is much more close related to the elliptic partial equations of the second order with variable coefficients. Now we need the further assumption for . It satisfies
. It satisfies

For



where 

where 
when

The corresponding fractional maximal operator with variable kernel is defined by
We can easily find that when

Especially, in the case
Many classical results about the fractional integral operator with variable kernel have been achieved [1] - [4] . In 1971, Muckenhoupt and Wheeden [5] had proved the operator 


The main purpose of this paper is to establish the boundedness of the fractional integral with variable kernel from 


means the characteristic function of a measurable set
2. Definition of Function Spaces with Variable Exponent
In this section we define Lebesgue spaces and Herz-Morrey spaces with variable exponent.
Let E be a measurable set in 

Definition 2.1. Let 

The space 
The Lebesgue spaces 
We denote

Then 



Let M be the Hardy-Littlewood maximal operator. We denote 


Let
Definition 2.2. Let 


Remark 2.1. (See [6] ) Comparing the Homogeneous Herz-Morrey Spaces with variable exponent with the homogeneous Herz spaces with variable exponent, where 
Obviously,
3. Properties of Variable Exponent
In this section we state some properties of variable exponent belonging to the class 

Proposition 3.1. (See [12] ) If 
then, we have
Proposition 3.2. (see [13] ) Suppose that





Now, we need recall some lemmas
Lemma 3.1. (See [14] ) Given 
Lemma 3.2. (See [15] ) Suppose that





Lemma 3.3. (See [16] ) Suppose that


then for all measurable function f and g, we have
Lemma 3.4. (See [17] ) Suppose that 

1) For any cube and

2) For any cube and

Lemma 3.5. (See [18] ) If


such that 
Lemma 3.6. (See [14] ) If


4. Main Theorem and Its Proof
In this section we prove the boundedness of fractional integral with variable kernel on variable exponent Herz- Morrey spaces under some conditions.
Theorem A. Suppose that


And let 



For all
Proof If 

If we denote
Then we have
Below, we first estimate 


Then we have
Since 

According to Lemma 3.4 and the formula


It follows that
Using Lemma 3.1, Lemma 3.5 and Lemma 3.6, we obtain
Hence we have
Remark that



If

Next we estimate
First we estimate of
To estimate of

Complete prove Theorem A.
Competing Interests
The authors declare that they have no competing interests.
Acknowledgments
This paper is supported by National Natural Foundation of China (Grant No. 11561062).
Cite this paper
Afif Abdalmonem,Omer Abdalrhman,Shuangping Tao, (2016) The Boundedness of Fractional Integral with Variable Kernel on Variable Exponent Herz-Morrey Spaces. Journal of Applied Mathematics and Physics,04,787-795. doi: 10.4236/jamp.2016.44089
References
- 1. Kenig, C. (1994) Harmonic Analysis Techniques for Second Order Elliptic Boundary Value Problems. American Mathematical Society, Providence.
http://dx.doi.org/10.1090/cbms/083 - 2. Calderón, A. and Zygmund, A. (1955) On a Problem of Mihilim. Transactions of the American Mathematical Society, 78, 209-224.
http://dx.doi.org/10.2307/1992955 - 3. Calderón, A. and Zygmund, A. (1978) On Singular Integral with Variable Kernels. Journal of Applied Analysis, 7, 221-238.
- 4. Christ, M., Duoandikoetxea, J. and Rubio de Francia, J. (1986) Maximal Operators Related to the Radon Transform and the Calderóon-Zygmund Method of Rotations. Duke Mathematical Journal, 53, 189-209.
http://dx.doi.org/10.1215/S0012-7094-86-05313-5 - 5. Muckenhoupt, B. and Wheeden, R. (1971) Weighted Norm Inequalities for Singular and Fractional Integrals. Transactions of the American Mathematical Society, 161, 249-258.
http://dx.doi.org/10.1090/S0002-9947-1971-0285938-7 - 6. Izuki, M. (2010) Boundedness of Commutators on Herz Spaces with Variable Exponent. Rendiconti del Circolo Matematico di Palermo, 59, 199-213.
http://dx.doi.org/10.1007/s12215-010-0015-1 - 7. Izuki, M. (2010) Fractional Integrals on Herz-Morrey Spaces with Variable Exponent. Hiroshima Mathematical Journal, 40, 343-355,.
- 8. Izuki, M. (2009) Boundedness of Vector-Valued Sublinear Operators on Herz-Morrey Spaces with Variable Exponent. Mathematical Sciences Research Journal, 13, 243-253.
- 9. Lu, S. and Xu, L. (2005) Boundedness of Rough Singular Integral Operators on the Homogeneous Morrey-Herz Spaces. Hokkaido Mathematical Journa, 34, 299-314.
http://dx.doi.org/10.14492/hokmj/1285766224 - 10. Izuki, M. (2009) Herz and Amalgam Spaces with Variable Exponent, the Haar Wavelets and Greediness of the Wavelet System. East Journal on Approximations, 15, 87-109.
- 11. Wang, Z. and Zhu, Y. (2014) Boundedness of Multilinear Fractional Integral Operators on Herz-Morrey Spaces with Variable Exponent. Journal of Lantong University (Natural Science Edition), 13, 60-68.
- 12. Cruz-Uribe, D. and Fiorenza, A. (2013) Variable Lebesgue Spaces. Foundations and Harmonic Analysis. Springer, New York.
- 13. Wu, H. and Lan, J. (2012) The Boundedness for a Class of Rough Fractional Integral Operators on Variable Exponent Lebesgue Spaces. Analysis in Theory and Applications, 28, 286-293.
- 14. Tan, J. and Liu, Z. (2015) Some Boundedness of Homogeneous Fractional Integrals on Variable Exponent Function Spaces. ACTA Mathematics Science (Chinese Series), 58, 310-320.
- 15. Cruz-Uribe, D., Fiorenza, A., Martell, J. and Pe’rez, C. (2006) The Boundedness of Classical Operators on Variable Lp Spaces. Annales Academiae Scientiarum Fennicae Mathematica, 31, 239-264.
- 16. Diening, L., Harjulehto, P., Hästö, P. and Ruziccka, M. (2011) Lebesgue and Sobolev Spaces with Variable Exponents. Springer-Verlag, Berlin Heidelberg.
http://dx.doi.org/10.1007/978-3-642-18363-8 - 17. Ding, Y. and Lu, S. (2000) Homogeneous Fractional Integrals on Hardy Spaces. Tohoku Mathematical Journal, 52, 153-162.
- 18. Izuki, M. (2010) Boundedness of Sublinear Operators on Herz Spaces with Variable Exponent and Application to Wavelet Characterization. Analysis Mathematica, 36, 33-50.
http://dx.doi.org/10.1007/s10476-010-0102-8
NOTES
*Corresponding author.