Received 27 September 2015; accepted 24 November 2015; published 27 November 2015

ABSTRACT

This paper presents a system representation that can be applied to the description of the interaction between systems connected through common boundaries. The systems consist of partial differential equations that are first order with respect to time, but spatially higher order. The representation is derived from the instantaneous multisymplectic Hamiltonian formalism; therefore, it possesses the physical consistency with respect to energy. In the interconnection, particular pairs of control inputs and observing outputs, called port variables, defined on the boundaries are used. The port variables are systematically introduced from the representation.

Keywords:

Symplectic Structure, Dirac Structure, Hamiltonian Systems, Passivity, Partial Differential Equations, Nonlinear Systems

1. Introduction

Energy is one of the most important concepts for describing physical systems. In analytical mechanics, an energy in the systems can be interpreted as a Hamiltonian. Hamiltonian systems can be characterized by symplectic structures [1] derived from the skew symmetry that cotangent bundles possess. Hamiltonian systems and their symplectic structures have been widely applied not only in physics, but in engineering, particularly, control theory [2] [3] . Specifically, in an electrical circuit, an energy is defined as the time integral of the product of currents and voltages. Energy flows between each circuit also balance if there is no dissipative element. Furthermore, the sum of currents balances between inflows and outflows at any node, and the directed sum of voltages around any closed loop is zero according to Kirchhoff law. Indeed, such properties have been generalized to various physical systems in terms of port-Hamiltonian systems [2] originated in bondgraph theory [4] . The above particular pairs with the physical dimension of power are called port variables, and the energy balances can be regarded as passivity [2] . A system is passive if and only if a finite amount of energy can be extracted from the system. In other words, energy changes in interactions can be observed by the port variables, and a supplied energy is less than a stored energy if a system is passive. Passivity-based controls via port-Hamiltonian system representations have been frequently used in control designs [3] .

This paper proposes the port-Hamiltonian representation of systems of higher order partial differential equations defined on a domain with a boundary. The representation can be formally formulated from the viewpoint of the multisymplectic formalism [5] [6] under the assumption of first order with respect to time, but possibly higher order with respect to spatial variables. The port representation for Hamiltonian systems with boundary energy flows was initiated by the distributed port-Hamiltonian system in [7] . The systems satisfy a power balance defined on the boundary; therefore, it can describe the interaction between the systems connected through common boundaries. Thus, passivity-based controls in this formulation can be enhanced as boundary energy controls. Various aspects of the distributed port-Hamiltonian systems have been studied, e.g., the implicit representation of distributed port-Hamiltonian systems [8] , and the relationship between field equations and distributed port-Hamiltonian systems [9] - [11] . The higher order representation of the distributed port-Hamiltonian systems has been proposed in, e.g., [12] [13] ; however, they are not related with the multisymplectic formalism.

Thus, we first relate higher order partial differential equations with the implicit Hamiltonian systems [14] . Next, we describe the implicit representation as a Dirac structure defined over the multisymplectic manifold in analogy with the first order formalizations [15] - [17] . Dirac structures [18] [19] are a unified concept of symplectic and Poisson structures. Then, we derive the Stokes variational differential from the fact that higher order derivatives yield variations of boundary port variables through integration by parts and Stokes theorem. Finally, we shows that the boundary energy balance and the Stokes-Dirac structure [7] [20] that is an extended Dirac structure for distributed port-Hamiltonian systems can be defined in the proposed higher order field port Hamiltonian systems with boundary energy flows.

This paper is organized as follows: In Section 2, we make a brief summary of port-Hamiltonian systems and explain the motivation of this study. Section 3 introduces mathematical preliminaries from some references. Section 4 presents the following three concepts under the assumption of time-spatial splitting: 1) an implicit Hamiltonian representation using the dual structure derived from the multisymplectic instantaneous formalism, 2) Stokes variational differential derived from the integration by parts formula, and 3) the implicit higher order field port Hamiltonian representation with boundary. Section 5 introduces the formal port representation for higher order partial differential equations from the implicit Hamiltonian representation. We call it higher order field port Hamiltonian systems with boundary energy flows. Finally, Section 6 illustrates two modeling examples.

2. Summary of Port-Hamiltonian Representations

This section explains the concept of port-Hamiltonian systems by means of a simple example of coupled multi- physical models, and the motivation of this work.

2.1. Port Representation for Lumped Parameter Energy Conserving Physical Systems

Let us consider the following model of the direct current motor consisting of an electrical circuit and an armature:

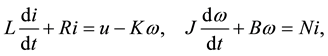(1)

where 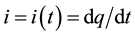is the current that is the time derivative of the electric charge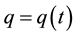, 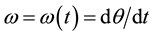is the velocity of the angle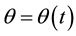, and u is the input voltage. In (1), the following constants are defined: the inductance L, the resistance R, the back electromotive force constant K, the inertia moment J, the viscous friction constant B, and the torque constant N. When the dissipative elements and the input are null, i.e., 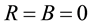and, the system (1) is energy conserving, and it can be formulated as the following standard Hamiltonian system:

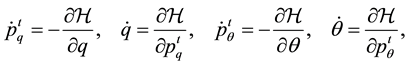(2)

where we have defined the Hamiltonian and the momenta as follows:

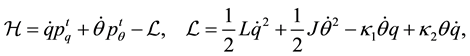(3)

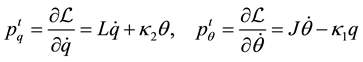(4)

with 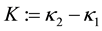and 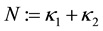for certain 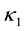and.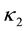

We shall augment the Hamiltonian system (2) as the following port-Hamiltonian system with the dissipations 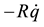and and the input u:

(5)

where we have defined the following variables called port variables:

(6)

and, in particular, and for and are called flows and efforts, respectively. Here, we can see that the electrical and mechanical subsystems are coupled by the interconnection of the effort variables: and.

Then, the summation consisting of the products of the pairs of the port variables is equivalent to the time derivative of the Hamiltonian, i.e., the total energy change of the system. Indeed, we can directly calculate the following power balance:

(7)

where we have used the relation. The relation (7) means that the dissipations and stabilize the system by decreasing the energy, and the product of the input and the output may affects the dissipation rate. Furthermore, the Hamiltonian can be controlled if we can find a suitable input satisfying for the desired Hamiltonian in the time interval. A finite amount of energy changes in interactions can be precisely observed by the product of an input-output pair if the system is passive. Hence, these controls are called passivity-based controls.

2.2. Distributed Port-Hamiltonian Systems

In the case of distributed parameter systems, the representation is called a distributed port-Hamiltonian system, and has the following formal structure:

(8)

called the Stokes-Dirac structure defined on the system domain with the boundary (see [7] for details), where d is the exterior differential operator, we have defined

(9)

for a Hamiltonian functional, is the space of differential k-forms, is the variational derivative with respect to the differential form, , and. Then, the power balance (7) is extended to the following relation described by differential forms:

(10)

The boundary integral term in (10) is generated from the domain integral term by Stokes theorem: for an n-form in the n-dimensional domain. Hence, the passivity-based controls can be enhanced as boundary energy controls by regarding and as a input-output pair, i.e., boundary port variables.

2.3. Motivation

As we have seen above, the port-Hamiltonian representations are important for the control of, e.g., nonlinear systems, distributed parameter systems, higher order systems and multi-physical systems from which it is difficult to obtain analytical solutions in a closed form. This paper derives a formal port-Hamiltonian representation of a given partial differential equation including higher order derivatives in terms of the multisymplectic formalism.

In this paper, we assume that a given system of partial differential equations is determined by variational problems. Such a system must be regarded as an energy conserving physical system [15] through Legendre transformations that map Lagrangian systems to Hamiltonian systems. This assumption comes from the fact that any system can be decomposed into a variational subsystem that can be determined by variational calculus and a non-variational subsystem that cannot be introduced from any Lagrangian on a contractible manifold [21] . For example, as we seen in (1), the dissipative terms and cannot be derived from any Lagrangian or Hamiltonian. On the other hand, Lagrangians of the first subsystem can be explicitly calculated by homotopy operators in terms of the exactness of vertical differential forms in variational bi-complex [22] [23] . Hence, we consider only the variational subsystems in this study.

3. Mathematical Preliminary

Mathematical notations used in this paper basically conform to those of the references [22] [24] [25] .

3.1. Multi index for Higher Order Derivatives

Let X be an -dimensional manifold. Let Q be a fiber manifold on X, and consider the r-th order jet bundle over Q. We denote the local coordinates of X, Q, and, respectively, by, , and, where, and. The multi index I describes all variables of the repeated combination of that mean higher order derivatives with respect to the variable, e.g.,. We the order of I by, and it is used as that means all derivatives up to the r-th order. Let be the time coordinate for and let be the spatial coordinates for. In some case, we use the abbreviation such as.

Example 1. Let, , and. We define the local coordinates of X by, and those of Q by. Then, the local coordinates of the jet bundle are for all. Note that q is described as a function of t, y; however, each element of is regarded as independent variables on the bundle. By using the summation convention, for example, we can interpret such as for.

3.2. Time-Spatial Splitting of State Space

Variational problems can be formalized as follows.

Definition 1. Consider the -form as a Lagrangian density of a functional. We define the variational derivative of the Lagrangian density as the -form

(11)

that determines the stationary condition of the variational problem, where, and is the vertical differential operator (see Sections B and C). In the following discussions, the variational derivative is lifted on.

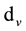
Let us consider the following control system as a main objective.

Assumption 1. A given system is defined on a contractible domain with a boundary, and it can be derived from a Lagrangian density in functional forms including derivatives that are first order with respect to the time coordinate and up to -th order with respect to spatial coordinates.

Under this assumption, the multi index I up to r-th order used for describing r-th order Lagrangians can be defined as, where the multi index K is of spatial coordinates for.

Example 2. In the case of, and, let be a local coordinates of Q on X. Then, by defining and, the local coordinates of can be described as. Without Assumption 1, I may include.

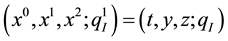
Furthermore, the following second assumption is important when we use the multisymplectic instantaneous formalism (see Section E).

Definition 2. Let us consider the time-spatial split domain consisting of a time interval and a spatial domain. Then, a system defined on at an instantaneous time is defined on.

Assumption 2. A Lagrangian density restricted to can be described as at a time in, where we denote the spatial (horizontal) volume form by.

Note that, we treat variables including time derivatives, e.g., in a bundle restricted to the spatial domain in this setting.

4. Implicit Hamiltonian Representation Induced from Distributions

In this section, we present a symplectic structure for distributions determined by partial differential equations in terms of the implicit Hamiltonian representation [14] . A distribution is a subbundle of a tangent bundle that is defined by a system dynamics, external constraints, and internal constraints generated by degenerate Lagrangians. On the other hand, a field Hamiltonian system is defined by the covariant Hamiltonian in the multisymplectic formalism [6] . However, the covariant Hamiltonian does not correspond to the typical Hamiltonian that are constant with respect to time evolution, e.g., for particle systems, but the instantaneous Hamiltonian derived from the time-spatial splitting.

4.1. Distributions

Definition 3. Consider a system of Pfaff equations on an n-dimensional manifold M, where for each a is a differential 1-form. Then, the submanifold N of M is called an integral manifold of if for any vector on the tangent space at each point, where.

Definition 4. Let M be an n-dimensional manifold M. A morphism associating an r-dimensional subspace of the tangent space with each point is called an r-th order distribution. The distribution is called regular if the dimension r is invariant.

The integrability of can be rephrased by distributions. That is, the r-dimensional distribution is defined by for each point, where.

4.2. Symplectic Structure Restricted to Distributions

The relationship between Lagrangian and Hamiltonian systems is given by Legendre transformations (see (65) in Section D). For classical field equations, the Legendre transformations (or Lagrangians) are not regular in general, and thus, they are not one-to-one. However, the Legendre transformation can reasonably work under the following weaker condition.

Proposition 1. [5] Let be an embedded closed subbundle of. Then, the Legendre transformation is called almost regular if is a submersion (i.e., is surjective) with respect to the image. In this case, there exists a vector field on such that for any vector field on.

Proposition 2. [5] The following conditions are equivalent:

1) satisfies the Euler-Lagrange equations,

2) satisfies the Cartan equations,

3) If is almost regular, satisfies the Hamilton-De Donder equations,

where is the space of all sections, and is the -th jet of the section.

Remark 1. Note that is not always the extremum of the original variational problem, i.e., Euler-Lagrange equations even if a certain is a Cartan equation, where is the natural projection. This correspondence is valid only if is regular [5] . Hence, we start from Euler-Lagrange equations in this paper.

Under the assumption of first order Lagrangians with respect to time, the covariant Legendre transformation in (65) is restricted the following instantaneous Legendre transformation:

(12)

where is the multi index with respect to spatial variables, and is the spatial total divergence. The term in the second equation of (12) is introduced from in of (65), because Lagrangian is first order with respect to time.

From the above preliminaries, we shall relate a distribution of Euler-Lagrange equations with a distribution of Hamiltonian systems on the multisymplectic manifold through the relations i) ® ii) ® iii) in Proposition 2. Indeed, the following Hamiltonian representation for can be defined.

Definition 5. Consider the -th multisymplectic manifold with the local coordinates

under Assumption 1. Then, the local coordinates of can be written as, because this results from the addition of the local coordinates of and the coordinates generated by the differential operator with respect to, and we have used the relations:,. On the other hand, the local coordinates of are, because it is given by the pairing of and arbitrary vector that is defined by between the vertical tangent and cotangent bundles [1] . Note that there is no adjoint variable of p defining an affine structure [5] (p. 214).

Now, we can consider the following induced symplectic structure induced from distributions.

Proposition 3. Let be the almost regular Legendre transformation and let be a regular distribution on Q that is restricted to. We restrict the multisymplectic -form over (see Section D) to, i.e., we define a skew symmetric bilinear form by. Then, there exists the following subbundle for each and a fixed p:

(13)

where we have defined, is the vertical tangent map of, and is the distribution lifted along the vertical tangent map of the canonical projection.

Proof. According to Proposition 2, there exists a vector field for any vector field. Thus, there exists also, where is the natural projection. Hence, the relation in (13) is resulted from the nature of the symplectic structure. Indeed, for a given, there always exists the corresponding -form that determines a Hamiltonian vector field.

Let us introduce Dirac structures on vector spaces form the references [2] [18] [19] .

Definition 6. A Dirac structure on a vector space A is a subspace such that, where is the dual space of A, is the orthogonal space of with respect to the symmetric pairing on such that for, and is the natural pairing between and A.

Corollary 1. in (13) is the (almost) Dirac structure.

Proof. If we fix the coordinate p of, i.e., the covariant Hamiltonian, then Equation (13) is the typical form of induced Dirac structures [15] .

5. Distirubted Port-Hamiltonian Systems with Higher Order Boundary Energy Flows

In this section, we derive a formal structure of distributed port-Hamiltonian systems with boundary energy flows including higher order derivatives from the previously discussed implicit Hamiltonian representation. The energy flows passing through boundaries of system domains are used for boundary interconnections, or passivity- based boundary controls.

5.1. Boundary Terms Generated by Integration by Parts

In higher order variational problems, the zero boundary condition is usually assumed for simplification or some other reason. Then, boundary terms generated by Stokes theorem after applying integration by parts are eliminated. Actually, these boundary terms are related with the boundary energy flows.

Let us recall such a calculation that yields the boundary term in variational calculus. We first define the following notation for simplification.

Definition 7. From the Legendre transformation in (65), we can derive the following variable:

(14)

where, , is the total differential operator (61), and we have set for.

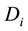
Now, we consider the Lagrangian density functional. The variational derivative of the Lagrangian density functional can be transformed by the integration by parts formula as follows:

(15)

where. By Stokes theorem [22] , for any, the first term in the right side of (15) can be transformed into

(16)

where is the total divergence that acts as, and is the volume -form on. For the integrands in (15) and (16), consider the operation of differential forms that separate a coefficient from a vertical basis. For example, can be decomposed into and. This operation is defined as follows.

Definition 8. For an -form, we define the integration by parts operator as the following local expression:

(17)

where we denoted, i.e., the style means

the set of the transformed local coordinates (A) on and (B) on, respectively. Here, untransformed coordinates under -th order are omitted in (17), and their numbers can be explicitly calculated by, and.

Remark 2. For a Lagrangian density restricted to the spatial domain in the time- spatial split space, the operation (17) can be also well defined. In this case, the boundary terms generated by Stokes theorem with respect to the time derivative in the total divergence are eliminated, because there is no boundary of a point in the time axis.

The repeated application of the integration by parts operator can yield all variations of boundary terms appeared in variational calculus.

Proposition 4. For some I, where, the v-th degree integration by parts operators is defined by

(18)

that can be expressed as the coordinate transformation

(19)

Proof. From the direct calculation of, we obtain the following representation on that is derived from that on:

(20)

The first bracket of (20) includes the nonzero part of the Euler-Lagrange equation; therefore, this operation is equivalent to the variational differential. The last r elements in the second bracket correspond to in (19) for.

5.2. Stokes Variational Differential

The symplectic structure induced from distributions does not have any information on boundary energy flows. In this section, we define a variational differential operator with boundary terms generated by integration by parts and Stokes theorem, called the Stokes variational differential. The Stokes variational differential can be used in the induced symplectic structure for relating a given Lagrangian with port-Hamiltonian representations.

Proposition 5. For an r-th order Lagrangian density that is first order with respect to time and -th order with respect to spatial coordinates, the following variational differential operation can be defined:

(21)

where (given as). We call the Stokes variational differential on with.

Before the proof of Proposition 5, we should prepare the following bundle maps. We first consider the map between and over.

Lemma 1. We can define the following bundle map:

(22)

Proof. This can be proven by the direct calculation with respect to the symplectic form (see Definition 5).

Lemma 2. By using the Legendre transformation, we can define the following bundle map under the first order assumption:

(23)

where, and p is defined by.

Proof. There exists the following bundle map under the assumption:

(24)

This can be proven in analogy with the diffeomorphism in the lumped parameter case, i.e.,

( [16] , p. 140, [26] ). The inverse map of (24) can be extended as a map on the affine bundle (23). Indeed, we have the bundle map between the bundle and the original bundle of the tangent affine bundle. Because the local coordinates of

are, in the case of first order with respect to time, the local coordinates of are, and those of are. Thus, under the assumption, we can regard and as, respectively, and by identifying and.

Next, we regard the derivative of Lagrangian density as a differential -form on in the above discussion by using.

Lemma 3. The standard variational derivative

(25)

can be regarded as the following derivative under the assumption of first order Lagrangians with respect to time:

(26)

where we have defined the inclusions, and.

Proof. By , and , we can rewrite (25) as

(27)

where we have used. Moreover, the inclusion yields the dual map

(28)

Under the assumption, we can specify by in the above equations.

Proof of Proposition 5: From Lemmas 1-3, we can see that the map is well-defined.

5.3. Local Expression of Induced Symplectic Structures

From the previous preparations, we can derive the relationship between the distribution and an instantaneous Hamiltonian system on that is described by the induced symplectic structure using the Stokes variational differential.

Definition 9. Let be a Lagrangian density that is first order with respect to time, and let be a regular distribution on Q. Consider the symplectic structure induced on in (13), and the Stokes variational differential on with in (21). Let be the image of, where we have defined. Then, we define the implicit higher order field Hamiltonian representation on with as

(29)

where.

Theorem 1. The local expression of the implicit higher order field port Hamiltonian representation on with determined by is given as follows:

(30)

where is the covariant momentum, and we have defined the null space. On the boundary, there is the following -form:

(31)

where, K is the multi index with respect to spatial coordinates, is the multi index generated by

repeated permutations (see Section B), and we have defined the spatial total divergence.

Proof. Let be the vector field on. For a vector field, we consider the following local expression of the symplectic form

(32)

where is the natural pairing between and. On the other hand, from the local expression of the Stokes variational differential on

(33)

we denote the 1-form fields by and. From the equivalent condition between the last relation in (13) and (32)

(34)

we obtain the condition

(35)

for any u and. Then, Equation (35) yields (30), because, and that can be derived from the Euler-Lagrange equation. Indeed, the pairing with respect to u gives the third relation in (30) as follows:

(36)

where corresponds to the boundary term in (31). The term (31) is obtained from the calculation in (20). Here, the total divergence with respect to time has been eliminated. Consequently, in (30), the first relation means a given vector field, the second relation is the definition of jet variables, the third relation is the Euler-Lagrange equation before applying integration by parts, and the fourth relation is the definition of the momentum.

The above representation can be converted to the following formal form of port representations [7] .

Corollary 2. The implicit higher order field port Hamiltonian system defined on with can be rewritten as the following port Hamiltonian system:

(37)

where, and we have defined the variables

(38)

for. We call and boundary port variables.

Proof. Form the third and second relations in (30), we can obtain the first and second rows in (37), respectively. The product of the pair of the third relation in (38) that is equivalent to the boundary term in (31), where in (31) has been interpreted as an infinitesimal variation of.

5.4. Power Balance and Passivity

This section derives the power balance of the Hamiltonian representation discussed in the previous section, and define the formal representation of higher order field port Hamiltonian systems with boundary energy flows.

In the time-spatial split space, the instantaneous Hamiltonian (70) on is given by

(39)

where. The following relation corresponds to the power balance of distributed port-Hamiltonian systems.

Proposition 6. The system (37) satisfies the power balance

(40)

Proof. The power balance can be derived from the interior product between the derivative of the instantaneous Hamiltonian (39) and arbitrary vector field is zero. Let be the generalized energy density of (39) defined on, where, and is the Whitney bundle with the local coordinates for and. Next, consider the pairing between and the vector field as follows:

(41)

where we have used, and the time total divergence is eliminated in the same way of the proof of Theorem 1. From the energy conservation, we obtain.

On the other hand, we have

(42)

By substituting (42) into (41), the integrand of (40) is given as follows:

(43)

By applying Stokes theorem to the integral of the third term of the second equation in (43), (40) is given.

Proposition 7. The system (37) is passive.

Proof. The Hamiltonian (39) and the power balance (40) correspond to the finite constant and the duality product before the time integration, respectively, in the definition of the passivity (see Section A).

Consequently, we at last reach the final result that means the system (37) is just a higher order representation of distributed port-Hamiltonian systems.

Theorem 2. The system (37) is the Stokes-Dirac structure.

Proof. We have already proven that the system (37) is a Dirac structure in Proposition 1. On the other hand, the power balance (40) corresponds with the main property of distributed port-Hamiltonian systems described by the Stokes-Dirac structure, and it can be regarded as the higher order version of the structure [12] .

6. Examples

This section presents two modeling examples.

6.1. Timoshenko Beam Equation

The 1-dimensional Timoshenko beam equation

(44)

is derived from the Lagrangian density functional on

(45)

where is the time coordinate, is the spatial coordinate along the longitudinal axis, is the shearing, is the rotation at each point in y, is the unit mass, is the moment of inertia, is the elastic stiffness, and is the shearing stiffness.

Let, , and. From and the maximum of higher order degrees in (44), we derive for. By defining with the local coordinate, we set and.

In (38), from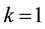, , , and, we obtain

(46)

where and we have defined

(47)

Hence, we have

(48)

where two lines form the first equation in (48) is equivalent to (44), and three lines from the bottom are equalities. Moreover, the system (48) satisfies

(49)

where note that Stokes theorem cannot be applied to; therefore the corresponding boundary term has not been defined.

6.2. Potential Boussinesq Equation

The 1-dimensional potential Boussinesq equation ([27] , p. 237) that expresses shallow water waves

(50)

is derived from the Lagrangian density functional defined on

(51)

where is the time coordinate, is the spatial coordinate along the water surface, and is the height of the wave.

Let, , and. We have defined with the local coordinate for, , and by and the maximum order in (50).

By substituting, , , and to (38), we get

(52)

where and we have defined

(53)

Hence, the following system representation is given:

(54)

where the first line of the first equation in (54) is equivalent to (50), and two lines from the bottom are equalities. Moreover, the system (54) satisfies

(55)

7. Conclusions

This paper derived the higher order field port Hamiltonian system with boundary energy flows from systems of higher order partial differential equations that are determined by variational problems in terms of the multisymplectic instantaneous formalism. By defining the symplectic structure induced from distributions and the Stokes variational differential including the integration by parts operators, we clarified the implicit Hamiltonian representation of the systems of higher order partial differential equations, and its local expression corresponds to the distributed port-Hamiltonian system.

In this paper, we assumed that Lagrangians are first order with respect to time, but possibly higher order with respect to spatial variables for simplification. This assumption can be generalized. On the other hand, the formal representation including time derivatives up to first order corresponds to the distributed port-Hamiltonian systems.

Acknowledgements

The author thanks Professor Bernhard Maschke for fruitful discussions on this study. This work was supported by JSPS Grants-in-Aid for Scientific Research (C) No. 26420415, and JSPS Grants-in-Aid for Challenging Exploratory Research No. 26630197.

Cite this paper

GouNishida, (2015) Hamiltonian Representation of Higher Order Partial Differential Equations with Boundary Energy Flows. Journal of Applied Mathematics and Physics,03,1472-1490. doi: 10.4236/jamp.2015.311174

References

Appendix

A. Passivity

Consider the following pairing between and:

(56)

for and, where is the duality product, U is a finite dimensional linear space, is its dual space, and we have defined the extended space that is the set of all measurable functions in truncated to a finite time interval. Note that the duality product corresponds to power.

Definition 10. Let. Then G is passive if there exists a constant H such that

(57)

where the left-side of (57) is assumed to be well-defined.

Hence, G is passive if and only if a finite amount of energy can be extracted from the system defined by G.

Corollary 3. For a point t in the time axis,

(58)

B. Differential Forms on Bundles

A differential -form defined on the r-th order jet bundle are defined by a horizontal i-form and a vertical j-form, where is the space of differential j-forms on, is a smooth function defined on, and and are different combination selected from a and I for.

Let be the space of differential -forms defined on. -forms such that are called n-forms, and their space is denoted by.

The exterior differential operator for -forms is defined by the vertical differential operator

(59)

and the horizontal differential operator

(60)

where the total differential operator with respect to is defined by

(61)

that is equivalent to partial differential, and. Note that, and, where is the weight of the index I [22] [24] , and for the index generated by the repeated permutation of the combination in I.

C. Euler-Lagrange Equations

An Euler-Lagrange equation is determined by the stationary condition of the variational derivative of a Lagrange density. If variables on boundaries are zero, the local expression of Euler-Lagrange equations is given by the stationary condition of

(62)

where is the -volume form, is the total differential operator with respect to all index in I, integration by parts is used in the second equality, and the term is eliminated by Stokes theorem under the assumption of the zero boundary condition.

D. Multisymplectic Covariant Formalism

The Hamiltonian representation of lumped parameter systems are determined by the symplectic 2-form on cotangent bundle, where is the canonical 1-form. Then, for a given Hamiltonian, Hamiltonian vector field is defined by ([1] , p. 187), where, is the interior product.

The (covariant) Hamiltonian representation of field equations are determined by the multisymplectic - form on the multisymplectic manifold ([5] , p. 211), where is the canonical -form. Then, is defined as the subbundle of over defining -forms

(63)

where the space of -forms over is defined by the space of all sections of -th degree exterior power cotangent -th jet bundle [5] , and the vertical tangent bundle has been defined as a vector subbundle determined by the tangent map for a bundle. Note that the local coordinates of the tangent bundle when those of the manifold X are, and the local coordinates of are when those of the bundle are, where those of are. Let for be the local coordinates of. Any in (63) can be locally written as

(64)

where we assume that the multi index satisfies. Then, is defined by using (64).

On the other hand, the covariant Lagrangian system can be defined as on by the Cartan form, where, and is the covariant Legendre transformation on

(65)

where is the pull-back, and are the local coordinates of for. The functions and in (65) give arbitrariness in the global expression of; therefore, this is not used in the local expression, i.e.,.

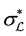
In the above, the covariant Lagrangian system determined by the variational problem of the r-th order Lagrangian density on is defined by the Cartan form on ([5] , p. 210). Note that the covariant Hamiltonian p determines the affine structure of that is the essential of the symplectic structure.

E. Multisymplectic Instantaneous Formalism

The instantaneous formalism is the covariant representation with time-spatial splitting. The time-spatial splitting is equivalent to choosing an infinitesimal supersurface parametrized by time in the configuration space Q. Bundles with time-spatial splitting consist of the Cauchy surface and time-spatial vector fields on Q. Then, means the direction of the time evolution of the system, and on transversally intersects to everywhere, where means the restricted Q to.

The instantaneous representation is defined on the space that consists of all sections of restricted to. For a given global section, the local coordinates of is given as ([6] , p. 379), where is the local coordinates of for. Then, the subbundle of that can be identified with the tangent bundle by choosing the direction of the time evolution of, where the local coordinates of are obtained from by using the multi index U with respect to time for. Hence, by restricting the system to, the spatial derivatives in are eliminated.

and are the vector bundle over with numbers of local coordinates, respectively, for and for. On the dual bundle of, i.e., , the instantaneous Hamiltonian systems are derived from the canonical form

(66)

where the instantaneous momentum

(67)

is calculated by integration by parts, and the weight

(68)

based on the combination have been defined.

Instantaneous Lagrange systems are determined on by [6, pp. 382], where the instantaneous Legendre transformation

(69)

is given by for and that are multi indexes with respect to time. The image in of the bundle map is the instantaneous primal constraint set. The instantaneous Hamiltonian on is defined as follows ([6] , p. 384):

(70)

Because possesses the (pre-)symplectic structure of, instantaneous Hamiltonian systems on are given by evolutional vector fields such that.