Journal of Applied Mathematics and Physics
Vol.02 No.13(2014), Article ID:52540,8 pages
10.4236/jamp.2014.213144
Comparison of Simulation Methods of Ion-Atomic Collisions in PIC-MC
Valeriy Sysun, Alexander Sysun, Vladimir Ignakhin, Viktor Titov, Alexander Tikhomirov
Department of Physical Engineering, Petrozavodsk State University, Petrozavodsk, Russia
Email: vsysun@psu.karelia.ru, ignahin@psu.karelia.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 October 2014; revised 25 November 2014; accepted 21 December 2014
ABSTRACT
The main ion-atomic collision treatment methods based on Monte-Carlo simulation are considered and discussed. We have proposed an efficient scheme for simulation of time between collisions taking into account cross-section dependence on ion velocity and random generation of ion velocities and scattering angles after collisions. The developed algorithm of simulation of interval between collisions takes into account the change of relative velocity of ion-atom pair as well as the change of cross-section of collision and atomic concentration. At the same time, unlike the widely used “null-collision” method, both the probability of collision and change of particles’ state which determines this probability are taken into consideration for each particle independently in time. The simulation results according to the techniques proposed are found to be close to the theoretical values of ion drift velocities. It is revealed that the “null-collision” method results in exceeding of drift velocity in strong and intermediate fields. At the same time the proposed method of accumulation of probability under the same conditions gives values close to theoretical ones. In weak fields calculated values of drift velocity in both methods exceed theoretical values to some small extent.
Keywords:
PIC-MC Simulation, Ion-Atomic Collisions, Discharge Plasma

1. Introduction
The simulation of plasma by Particle-in-Cell Monte-Carlo (PIC-MC) method has received widespread application in calculations of ion current on probe and dust particle and plasma simulation of glow and high-frequency discharges [1] - [6] . The important stage in PIC-MC method is simulation of ion collisions with neutral atoms. It includes interval simulation between collisions, simulation of velocity and direction of ion motion after collision.
The drift time of an ion up to the next collision has probabilistic nature: probability of collisions for the time
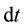 doesn’t depend on the previous way and proportional to
doesn’t depend on the previous way and proportional to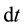 :
: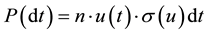 ,
,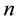 ―concentration of atoms,
―concentration of atoms,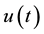 ―relative velocity ion-atom,
―relative velocity ion-atom,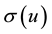 ―cross-section of collision.
―cross-section of collision.
Let us assume by this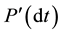 ―probability of absence of collision for the time
―probability of absence of collision for the time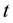 . Then the probability of collision for
. Then the probability of collision for 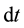 after non-collision time
after non-collision time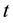 , determining decrease of
, determining decrease of 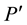 as
as 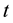 increases to
increases to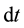 , is
, is
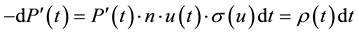 ,
,
where 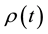 is probability density. Equations (1) are the expressions for probability of absence of collision for the time
is probability density. Equations (1) are the expressions for probability of absence of collision for the time 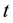 and for probability density
and for probability density

Equation (2) is probability of collision since the time 

The following methods of simulation of the interval between collisions are applied.
2. Review of Methods of Simulation of the Interval between Collisions
2.1. Constant Time between Collisions [7] - [9]
Equation (3) is approximation of constant time between collisions

This approximation is correct at inverse dependence of cross-section on velocity.
In the supposition based on Equation (3) 

with the help of uniformly distributed at [0,1] random value “rand”. Equation (4) shows the expression for random value “rand”

In Equation (4) 

2.2. Constant Path Length [5] [6] [9] [10]
Equation (5) is the expression for path length in this case

Let us replace a variable in Equation (1)

For each ion path length is simulated after each collision. Equations (7) are the expressions for ion’s path length

The achievement of individual path length by each ion is checked by summing up its ways on each time step
The approximation of constant path length takes into account the change of ion velocity, however the cross- section of collisions is considered to be constant here that can be accepted with some approximation at resonant charge exchange. In [9] a problem of the method considered has been revealed. If the method of constant path length was used, the decrease of average ion energy was observed because of more frequent collisions of fast ions transferring energy to atoms and absence of direct Maxwellian process among charged particles in PIC.
2.3. Simulation of Collision Probability on Each Time Step [1] [3] [11]
For the time interval 


While each ion is simulated, if 


respond to the current time point
2.4. “Null-Collision” Algorithm
This algorithm is considered in details in [2] and actively used [2] [4] [12] . At first, the maximum value of
product 


tion (9) is constant conditional collision probability for the time

Then, in case of total number of ions N on each time step, the number of ion is simulated P0N times. For this ion rand is simulated again and the type of collision or the absence of it is defined. Equation (10) is the condition of event that k-type of collision occurs:

At 

Treatment methods of collision probability are combined in the “null-collision” technique. At first, the number of the ion is determined in the ensemble, and then the type of collision or its absence is defined through the change of ion state in time. The number of arithmetic operations 
In [12] “null-collision” method is applied to define the collision probability on each time step. At 


There is a variety of revisions of the “null-collision” algorithm used for simulation of electron-atom collisions when cross-sections are strongly dependent on electrons’ energy. Thus, in the method of constant time between
collisions the time interval is determined by maximum possible value of 


3. Improvement of Methods and Simulation Experiment
3.1. Improvement of Methods of Constant Path Lengths and Time between Collisions―The Method of Accumulation of Probability
It is possible to offer the following method taking into account the change of value 

then we will have 


Equations (13) are the expressions if individual ion is simulated:

Summing up by steps in time lasts up to the reaching of equality in Equation (13). In such a way, this algorithm takes into account the change of 


3.2. Simulation of Energy and Direction of Ion Motion after the Collision
Direction of ion motion after the collision is characterized by taking into account deviation from original direction 





At elastic scattering of ion on atom in these works scattering goes only forward. Equation (15) is the formula for 

Equation (16) is energy after scattering:

In works [11] [14] at elastic collisions the law of ion-atom interaction is stated. Impact parameter and relative velocity are simulated by randomizer and then depending on the minimal radius of approximation the angles and ion energies are calculated after collision. This method makes simulation process significantly more difficult. At the same time Equations (15), (16) don’t take into account the transfer of energy from atoms to ions that is the most significant at weak fields.
Let us consider Monte-Carlo algorithm of simulation of elastic ion-atom collisions on the model of elastic spheres. In this model in Figure 1 normal and tangential components of ions’ velocity after collision are:




Further we consider ion motion in their own gas



Figure 1. Model of elastic spheres.
of ion and atom velocities to normal. For the angle 


rameter,

For the density of probability we have



For strong fields if we ignore atom velocity






However, in weak fields an ion can get significant additional velocity from an atom in collisions.
Equation (19) is ions’ velocity after collision in this case






Let us consider atom 

Equation (20) is the expression for simulation after introducing the new parameter

The integral can be replaced by an analytic expression, having approximation with accuracy up to 3%. Equation (23) is the approximation for

The results of calculations presented in Table 1 reveal the approximation (23) to be close to the exact values.
Equation (24) is density of probability of 


It determines

Angle 

Let us have angle 




It is here that we need angle 
At resonant charge exchange angle 

3.3. Simulation Experiment
To compare “null-collision” method and method of accumulation of probability the simulation experiment of ion motion in constant electric field 
Figure 2. Angles of ion deviation:

Table 1. Comparison of approximated 

The number of ions was taken as equal to 105. Original ion velocities had Maxwell distribution with the temperature of atoms by Equations (23) and (24). The interval of time 





Equations (27) are non-dimensional variables accepted:

With equations of motion 

Obtained average drift velocities were compared with theoretical ones [15] [16] .
Equations (28) are drift velocities for resonant charge exchange and elastic collision in weak fields when drift velocity is less than thermal velocity:

at resonant charge exchange and elastic interaction correspondingly, where 


Equation (30) is the approximation used in intermediate fields:

The results of simulation are given in Table 2 and Table 3
Table 2. Value of drift velocity 
Table 3. Value of drift velocity 
It is necessary to mention that computing time in “null-collision” method (in the same conditions) turned out to be 2 - 3 times less than in method of accumulation of probability. However, in case of large 
Method of accumulation of probability in strong and intermediate fields gives values close to theoretical ones. Accuracy is limited only by fluctuations of average velocity increasing when the total number of ions decreases and their temperature goes up. In weak fields calculated values of drift velocity in both methods exceed theoretical values to some extent (up to 5%). It can be caused by the fact that when Equations (28) are obtained inte-
grated square velocity is accepted as an average relative velocity:
4. Conclusion
The given effective models of calculating time between collisions by the method of accumulation of probability and ion angle velocities’ simulation after collision on the basis of solid spheres result in ion drift velocities close to theoretical ones and can be applied in the process of simulation of ion motion in heterogeneous plasma with non-constant concentration of atoms and ions and dependence of cross-section on velocity.
Acknowledgements
The work is done by the support of Program of strategic development of Petrozavodsk State University from 2012 to 2016, Ministry of Education of Russian Federation, contract No. 3.757.2014/K.
References
- Birdsall, C.K. (1991) Particle-in-Cell Charged-Particle Simulations, plus Monte Carlo Collisions with Neutral Atoms, PIC-MCC. IEEE Transactions on Plasma Science, 19, 65-85. http://dx.doi.org/10.1109/27.106800
- Vahedi, V. and Surendra, M. (1995) A Monte Carlo Collision Model for the Particle-in-Cell Method: Applications to Argon and Oxygen Discharges. Computer Physics Communications, 87, 179-198. http://dx.doi.org/10.1016/0010-4655(94)00171-W
- Zobnin, A.V., Nefedov, A.P., Sinel’Shchikov, V.A. and Fortov, V.E. (2000) On the Charge of Dust Particles in a Low-Pressure Gas Discharge Plasma. Journal of Experimental and Theoretical Physics, 91, 483-487. http://dx.doi.org/10.1134/1.1320081
- Cenian, A., Chernukho, A., Bogaerts, A., Gijbels, R. and Leys, C. (2005) Particle-in-Cell Monte Carlo Modeling of Langmuir Probes in an Ar Plasma. Journal of Applied Physics, 97, Article ID: 123310. http://dx.doi.org/10.1063/1.1938275
- Sysun, A.V., Sysun, V.I., Khakhaev, A.D. and Shelestov, A.S. (2008) Charge and Potential of a Dust Grain versus the Intergrain Distance and Establishment of the Latter in a Low-Pressure Plasma. Plasma Physics Reports, 34, 501-507. http://dx.doi.org/10.1134/S1063780X08060068
- Sysun, V.I. and Ignakhin, V.S. (2014) Simulations of the Ion Current to a Probe in Plasma with Allowance for Ionization and Ion-Neutral Collisions: I. Spherical Probe. Plasma Physics Reports, 40, 101-109. http://dx.doi.org/10.1134/S1063780X14010097
- Kim, H.C., Iza, F., Yang, S.S., Radmilović-Radjenović, M. and Lee, J.K. (2005) Particle and Fluid Simulations of Low-Temperature Plasma Discharges: Benchmarks and Kinetic Effects. Journal of Physics D: Applied Physics, 38, Article ID: R283. http://dx.doi.org/10.1088/0022-3727/38/19/R01
- Vaulina, O.S., Repin, A.Y. and Petrov, O.F. (2006) Empirical Approximation for the Ion Current to the Surface of a Dust Grain in a Weakly Ionized Gas-Discharge Plasma. Plasma Physics Reports, 32, 485-488. http://dx.doi.org/10.1134/S1063780X06060055
- Šimek, J. and Hrach, R. (2006) Comparison of Collision Treatment Methods in PIC-MC Plasma Simulation. Czechoslovak Journal of Physics, 56, B1086-B1090. http://dx.doi.org/10.1007/s10582-006-0331-z
- May, P.W., Field, D. and Klemperer, D.F. (1992) Modeling Radio-Frequency Discharges: Effects of Collisions upon Ion and Neutral Particle Energy Distributions. Journal of Applied Physics, 71, 3721-3730. http://dx.doi.org/10.1063/1.350882
- Nanbu, K. and Kitatani, Y. (1995) An Ion-Neutral Species Collision Model for Particle Simulation of Glow Discharge. Journal of Physics D: Applied Physics, 28, 324. http://dx.doi.org/10.1088/0022-3727/28/2/015
- Boeuf, J.P. and Marode, E. (1982) A Monte Carlo Analysis of an Electron Swarm in a Nonuniform Field: The Cathode Region of a Glow Discharge in Helium. Journal of Physics D: Applied Physics, 15, 2169. http://dx.doi.org/10.1088/0022-3727/15/11/012
- Skullerud, H.R. (1968) The Stochastic Computer Simulation of Ion Motion in a Gas Subjected to a Constant Electric Field. Journal of Physics D: Applied Physics, 1, 1567. http://dx.doi.org/10.1088/0022-3727/1/11/423
- Maiorov, S.A. (2009) Ion Drift in a Gas in an External Electric Field. Plasma Physics Reports, 35, 802-812. http://dx.doi.org/10.1134/S1063780X09090098
- McDaniel, E.W. and Mason, E.A. (1973) Mobility and Diffusion of Ions in Gases. Wiley, New York.
- Smirnov B.M. (2008) The Sena Effect. Physics-Uspekhi, 51, 291-293. http://dx.doi.org/10.1070/PU2008v051n03ABEH006542










